Теорема ПИФАГОРА Теорема В прямоугольном треугольнике квадрат

Теорема ПИФАГОРА

Теорема! В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

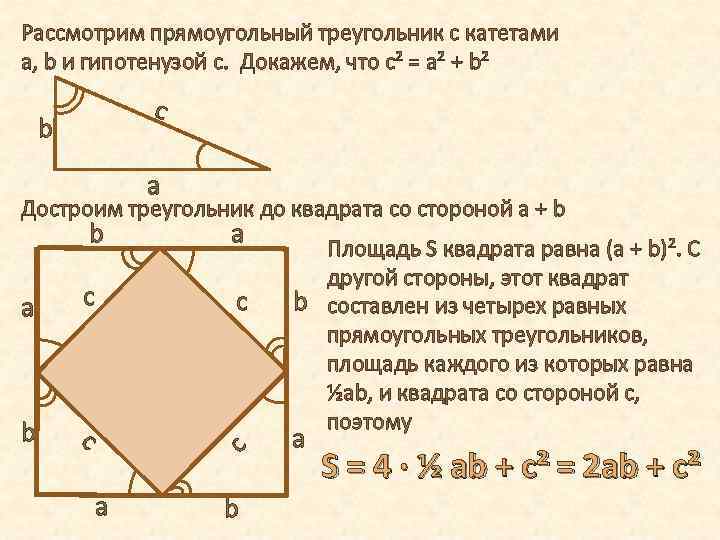Рассмотрим прямоугольный треугольник с катетами a, b и гипотенузой с. Докажем, что с² = а² + b² с b a Достроим треугольник до квадрата со стороной а + b a a с с b a b Площадь S квадрата равна (а + b)². С другой стороны, этот квадрат b составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна ½ab, и квадрата со стороной с, поэтому a S = 4 · ½ ab + c² = 2 ab + c²

Таким образом откуда (a + b)² = 2 ab + c² c² = a² + b² Теорема доказана.

История теоремы. Интересная история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифагора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора. Возможно, что тогда еще не знали ее доказательства, а само соотношение между гипотенузой и катетами было установлено опытным путем на основе измерений. Пифагор, по-видимому, нашел доказательство этого соотношения. Сохранились древние предания, что в честь своего открытия Пифагор принес в жертву богам быка, по другим свидетельствам – даже сто быков. На протяжении последующих веков были найдены различные другие доказательства теоремы Пифагора. В настоящее время их насчитывается более ста. Многие известные мыслители и писатели прошлого обращались к этой замечательной теореме и посвятили ей свои строки.

Теорема, обратная теореме Пифагора Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.

Пусть в треугольнике ABC AB² = AC² + BC². Докажем, что угол С прямой. Рассмотрим прямоугольный треугольник A₁ B₁ C₁ с прямым углом С₁, у которого A₁ C₁ = AC и B₁ C₁ = ВС. По теореме Пифагора А₁ В₁² = А₁ С₁² + В₁ С₁² , и, значит, А₁ В₁² + АС² + ВС². Но АС² + ВС² = АВ² по условию теоремы. Следовательно, А₁ В₁² = АВ² , откуда А₁ В₁ = АВ. Треугольники АВС и А₁ В₁ С₁ равны по трем сторонам, поэтому LC = LC₁ , т. е. треугольник АВС прямоугольный с прямым углом С. Теорема доказана.

По теореме, обратной теореме Пифагора, треугольник со сторонами 3, 4 и 5 является прямоугольным: 5² = 3² + 4². Прямоугольными являются также треугольники со сторонами 5, 12, 13, 8, 15, 17 и 7, 24, 25. Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются ПИФАГОРОВЫМИ ТРЕУГОЛЬНИКАМИ. Можно доказать, что катеты а, b и гипотенуза с таких треугольников выражаются формулами а = 2 k · m · n, b = k (m² - n²), c = k (m² + n²), где k, m и n – любые натуральные числа, такие, что m › n.

Треугольники со сторонами 3, 4, 5 часто называют ЕГИПЕТСКИМ ТРЕУГОЛЬНИКОМ, так как он был известен еще древним египтянам. Для построения прямых углов египтяне поступали так: на веревке делали метки, делящие ее на 12 равных частей, связывали концы веревки и растягивали на земле с помощью кольев в виде треугольника со сторонами 3, 4 и 5. Тогда угол между сторонами, равными 3 и 4, оказывался прямым.