Теорема Пифагора и её применение Пребудет вечной истина

Теорема Пифагора и её применение Пребудет вечной истина, как скоро Ее познает слабый человек! И ныне теорема Пифагора Верна, как и в его далекий век! Авторы: Роппель Виктория Молоствова Ирина Учащиеся 8 Б класса Руководитель: Резина Лилия Владимировна, учитель математики

Цель: Гипотеза: Теорему Пифагора можно применять не только Выяснить области применения теоремы при решении математических задач, но и задач Пифагора. Задачи: прикладного характера. Методы исследования: теоремы • Изучить историю открытия • • Пифагора. 1. Изучение и анализ теоретического Исследовать различные методы материала. доказательства данной теоремы. 2. Практическое выполнение исследования, Выяснить в каких сферах деятельности сравнение результатов. применяется эта теорема. 3. Метод применение теоремы при решении Показатьизмерения, анкетирование. задач прикладного характера.

Пифагор (570 -490 г. до н. э. ) Древнегреческий математик, философ. Родился в Сидоне Финикийском. В 18 лет покинул дом, в ходе странствий повстречал множество мудрецов своего времени. Во второй половине жизни учредил братство, члены которого именовались пифагорейцами. Сообществом было сделано множество открытий в арифметике и геометрии.

КВАДРАТ ГИПОТЕНУЗЫ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА РАВЕН СУММЕ КВАДРАТОВ КАТЕТОВ. Китай "Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4". Египет – 24 в. до н. э Построение прямых углов при помощи прямоугольных треугольников со сторонами 3, 4, 5: 3² + 4² = 5². Междуречье – 21 в. до н. э Вычисление гипотенузы прямоугольного треугольника. Индия – 18 в. до н. э Теорема о квадрате гипотенузы.

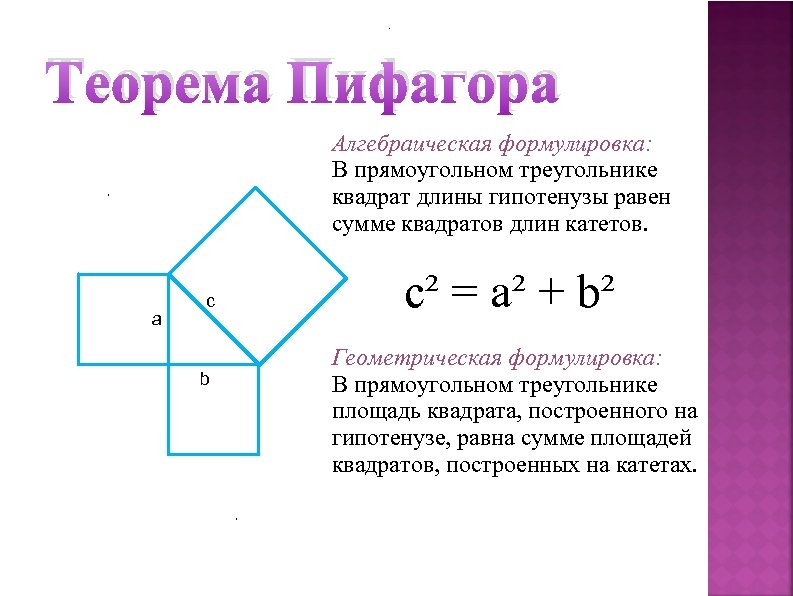
Теорема Пифагора Алгебраическая формулировка: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. а c b c² = a² + b² Геометрическая формулировка: В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

«ПИФАГОРОВЫ ШТАНЫ — НА ВСЕ СТОРОНЫ РАВНЫ» .

Доказательство Пифагора а а a² с² b b b² b + =

Социологический опрос Является ли Пифагор открывателем теоремы c²=a²+b²? • Был – 15 • Не был – 12 Сколько существует доказательств теоремы Пифагора: • • менее 10 – 15 не более 50 – 6 не более 200 – 0 более 300 – 6

Землемерие. Для построения прямых углов при планировке земельных участков и сооружения зданий. Землемеры Древнего Египта для построения прямого угла использовали бечёвку, разделённую узлами на 12 равных частей. Треугольник со сторонами 3, 4, 5 называют египетским треугольником.

Архитектура Верхние части окон расчленяются каменными ребрами, которые играют роль орнамента и способствуют прочности окон. Окна готического стиля Окна романского стиля При конструировании рамы, зная радиус большого круга, можно рассчитать радиус малого круга.

Строительство Двускатная крыша детского сада № 7 по ул. Коммунистическая, 21. Длина балки - 12 м Высота крыши – 3, 7 м Длина стропил – 7 м F Двускатная крыша в сечении – равнобедренный треугольник: AB=BC=6 м, BF=3, 7 м. Тогда длину стропила AF вычисляем по теореме Пифагора: м А Вывод: строители крыши при строительстве применили известную теорему. В С

Физика. Молниеотвод. ; h=51, 4: 2=25, 7 м. Определим наименьшую доступную высоту молниеотвода на двускатной крыше детского сада. Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты. Размеры крыши a=50 м и b=12 м. O O a h – высота молниеотвода. O –Если установить молниеотвод основание молниеотвода. Если установить молниеотвод на крыше посередине её ширины s – на углу крыши, то: расстояние от посередине крыши основания молниеотвода до предмета. крыше посередине её длины O O s= h= 25, 7: 2 = 12, 85 мм h=50: 2=25 м. h=27, 7: 2=13, 85 м. h=51, 4: 2=25, 7 м. Таким образом, знание теоремы Пифагора пригодится нам и в изучении физики. b

Мобильная связь Какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе R, если известно, что радиус Земли равен 6 380 км? Согласно свойству касательной: Δ ВСО – прямоугольный (∠С=90°). Пусть AB = h=x км, BC = R км, OC = r = 6380 км, OB = OA + AB, OB = r + x Используя теорему Пифагора, получаем: ⇒ ⇒ Итак, длина вышки должна быть: км.

Мобильная связь Можно определить радиус зоны А) Если известен радиусвышки, зная покрытия или высоту самой зоны одну из данных характеристик этой покрытия R=20 км, то вышки. h = 31 м – высота вышки. Б) Если известна высота вышки h = 50 м = 0, 05 км, то R=25, 3 км.

Литература Английский писатель О. Хаксли «Юный Архимед» Советский писатель Евгений Велтистов «Приключения Электроника»

Ф. А. БРОННИКОВ (1827 -1902) «ГИМН ПИФАГОРЕЙЦЕВ ВОСХОДЯЩЕМУ СОЛНЦУ» .

В ГРЕЦИИ БЫЛА ВЫПУЩЕНА ПОЧТОВАЯ МАРКА Пифагор – «убеждающий речью» «Теорема Пифагора. Эллас. 350 драхм» .

ПАМЯТНИК ПИФАГОРУ. ПОРТ ГОРОДА ПИФАГОРИЯ. Катет, лежащий в основании треугольника - мраморный, гипотенуза и фигура самого Пифагора в виде второго катета - медные.

Теорема Пифагора в задачах Области применения теоремы Пифагора: авиация, проектирование, военное дело, криминалистика, космонавтика. Головоломка Пифагора (Приложение 4). Квадрат разрезается так: E, F, K, L – середины сторон квадрата, О – центр квадрата, ОМ EF, NF EF Из семи частей квадрата составить снова квадрат, прямоугольник, равнобедренный треугольник, трапецию. На ОГЭ в модуле «Геометрия» обязательно есть задачи, решаемые с помощью этой теоремы (Приложение 5).

Заключение В ходе исследования мы: Выводы: • • провели социологический опрос среди учащихся 8 Теорема Пифагора по праву считается самой классов ивподвели результаты; важной курсе геометрии. • Заслуга Пифагора состоит в том, что он дал • изучили историю открытия теоремы Пифагора; полноценное научное доказательство этой теоремы. • рассмотрели различные методы доказательства • этой теоремы; Теорема Пифагора является единственной теоремой со столь внушительным числом • рассмотрели ряд(367) доказательств практических задач на • применение теоремы Пифагора; Исключительная важность теоремы состоит в том, что она позволяет находить высоту • выяснили её практическую значимость в повседневной объектов и расстояния до недоступных жизни. предметов.

Практическое применение Землемерие – проведение на местности перпендикулярных линий. Астрономии – вычисление пути светового луча, например, из космического корабля, расчет расстояния от корабля до наиболее отдаленных от него и видимых космонавтом участков поверхности Земли. Строительство – нахождения длины стропил крыши и её поверхности, разбивка контура здания. Мобильная связь – определение радиуса покрытия вышки, зная её длину, и обратное. Архитектура – конструирование рамы окон в зданиях готического и ромaнского стиля.

Спасибо за внимание!