Теорема о биссектрисе и медиане треугольника Презентацию подготовил Роман Ириоглов 9 Г
Теорема о медиане l В произвольном треугольнике ABC длину медианы CM можно выразить через длины сторон этого треугольника следующим образом: CM=1/2 • √(2 • AC² + 2 • CB² - AB²)
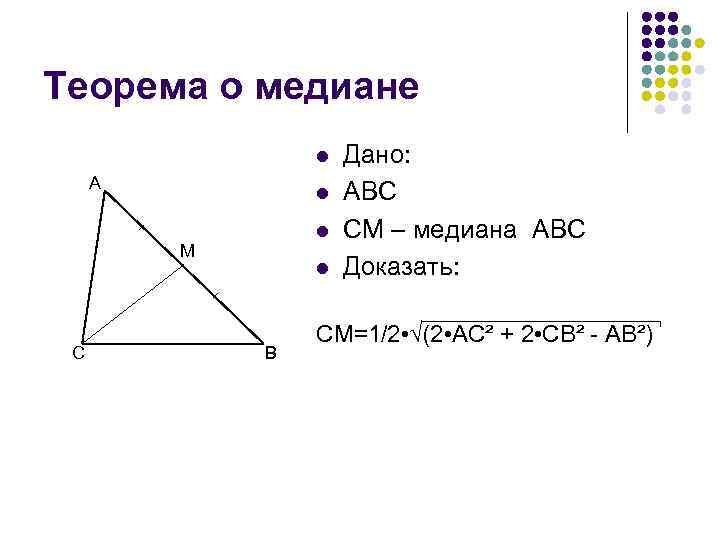
Теорема о медиане l A l l M C l B Дано: ABC CM – медиана ABC Доказать: CM=1/2 • √(2 • AC² + 2 • CB² - AB²)
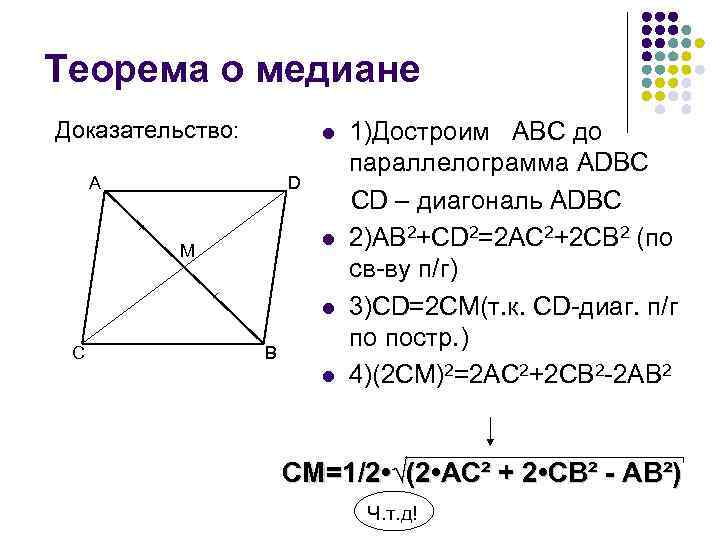
Теорема о медиане Доказательство: l A D l M l C B l 1)Достроим ABC до параллелограмма ADBC CD – диагональ ADBC 2)AB 2+CD 2=2 AC 2+2 CB 2 (по св-ву п/г) 3)CD=2 CM(т. к. СD-диаг. п/г по постр. ) 4)(2 CM)2=2 AC 2+2 CB 2 -2 AB 2 CM=1/2 • √(2 • AC² + 2 • CB² - AB²) Ч. т. д!
Задача Найдите длины отрезков, на которые делится медиана CM треугольника ABC точкой пересечения медиан O, если AC =√ 3, BC=2, AB=√ 5.
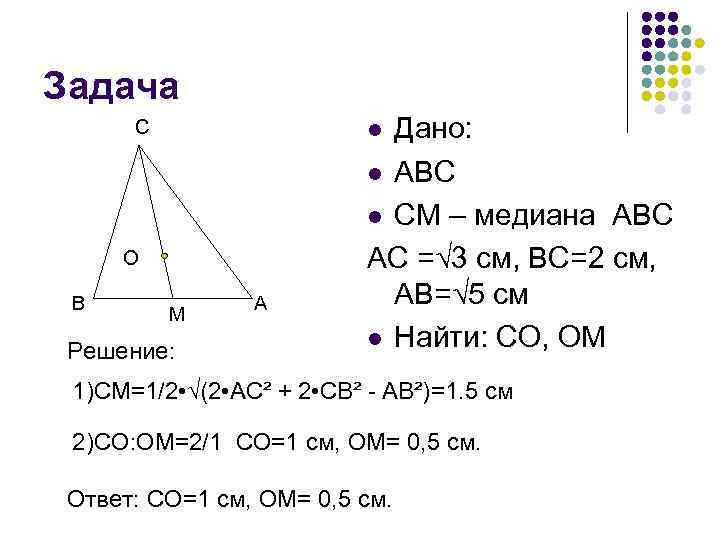
Задача C O B Дано: l ABC l CM – медиана ABC AC =√ 3 см, BC=2 см, AB=√ 5 см l Найти: CO, OM l M Решение: A 1)CM=1/2 • √(2 • AC² + 2 • CB² - AB²)=1. 5 см 2)CO: OM=2/1 CO=1 см, OM= 0, 5 см. Ответ: CO=1 см, OM= 0, 5 см.
Теорема о биссектрисе l В произвольном треугольнике ABC длину биссектрисы CD можно выразить через длины сторон этого треугольника следующим образом: AD= 1/(AB+AC)√AB*AC*(AB+AC+BC)(AB+AC-BC)
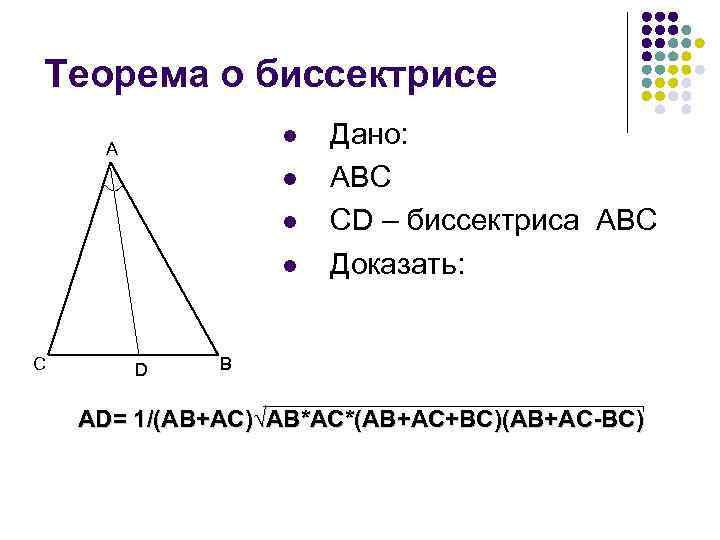
Теорема о биссектрисе l A l l l C D Дано: ABC CD – биссектриса ABC Доказать: B AD= 1/(AB+AC)√AB*AC*(AB+AC+BC)(AB+AC-BC)
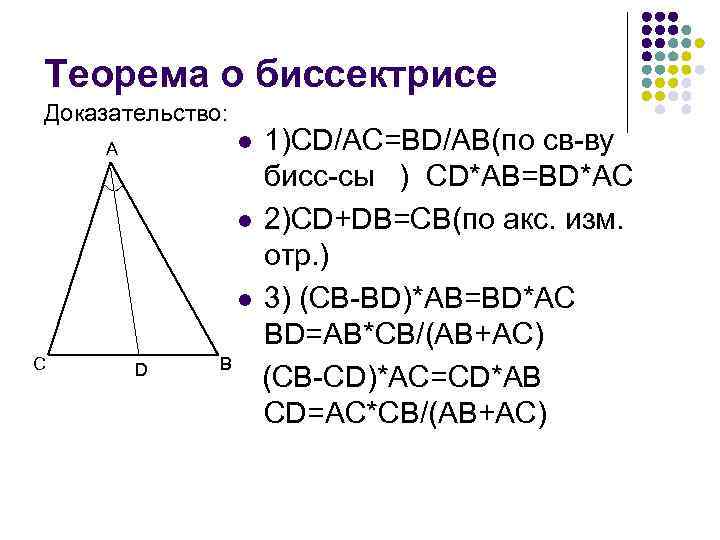
Теорема о биссектрисе Доказательство: C 1)CD/AC=BD/AB(по св-ву бисс-сы ) CD*AB=BD*AC l 2)CD+DB=CB(по акс. изм. отр. ) l 3) (CB-BD)*AB=BD*AC BD=AB*CB/(AB+AC) B (CB-CD)*AC=CD*AB CD=AC*CB/(AB+AC) l A D
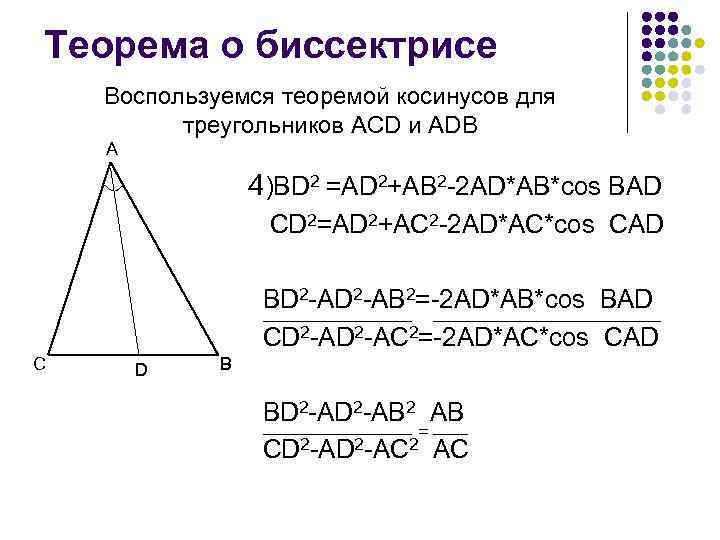
Теорема о биссектрисе Воспользуемся теоремой косинусов для треугольников ACD и ADB A 4)BD 2 =AD 2+AB 2 -2 AD*AB*cos BAD CD 2=AD 2+AC 2 -2 AD*AC*cos CAD BD 2 -AB 2=-2 AD*AB*cos BAD CD 2 -AC 2=-2 AD*AC*cos CAD C D B BD 2 -AB 2 AB = 2 -AD 2 -AC 2 AC CD
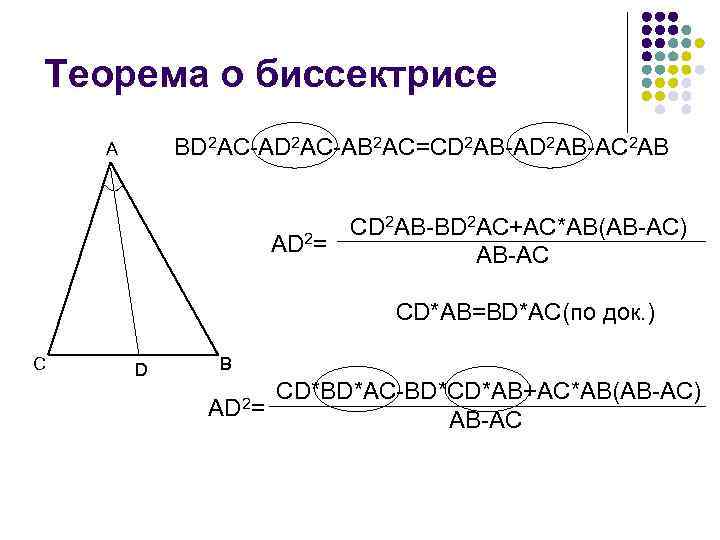
Теорема о биссектрисе BD 2 AC-AB 2 AC=CD 2 AB-AC 2 AB A CD 2 AB-BD 2 AC+AC*AB(AB-AC) AD 2= AB-AC CD*AB=BD*AC(по док. ) C D B AD 2= CD*BD*AC-BD*CD*AB+AC*AB(AB-AC) AB-AC
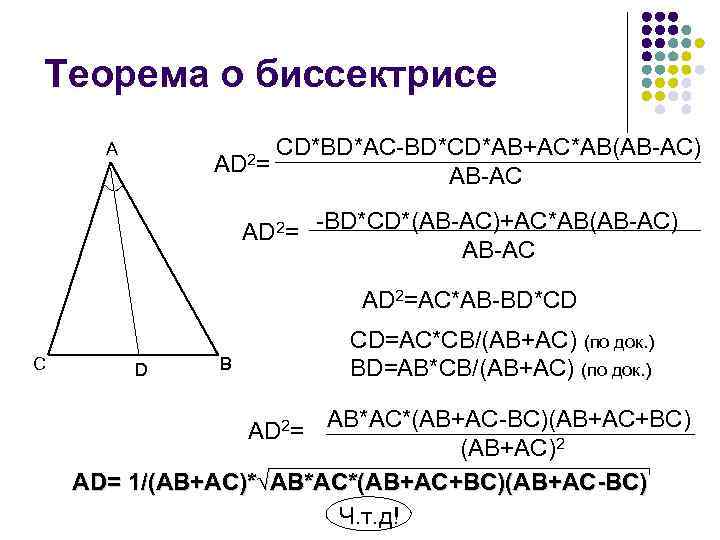
Теорема о биссектрисе A AD 2= CD*BD*AC-BD*CD*AB+AC*AB(AB-AC) AB-AC AD 2= -BD*CD*(AB-AC)+AC*AB(AB-AC) AB-AC AD 2=AC*AB-BD*CD C D B CD=AC*CB/(AB+AC) (по док. ) BD=AB*CB/(AB+AC) (по док. ) AD 2= AB*AC*(AB+AC-BC)(AB+AC+BC) (AB+AC)2 AD= 1/(AB+AC)*√AB*AC*(AB+AC+BC)(AB+AC-BC) Ч. т. д!
Задача Найдите площадь квадрата, стороной которого является биссектриса AD треугольника ABC, где AC=2 см, AB=3 см, BC=4 см
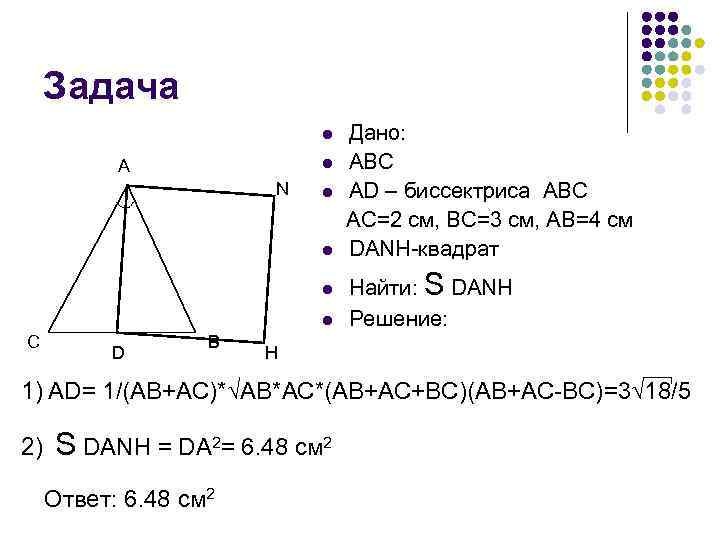
Задача l l A N l l C D B Дано: ABC AD – биссектриса ABC AC=2 см, BC=3 см, AB=4 см DANH-квадрат Найти: S DANH Решение: H 1) AD= 1/(AB+AC)*√AB*AC*(AB+AC+BC)(AB+AC-BC)=3√ 18/5 2) S DANH = DA 2= 6. 48 см 2 Ответ: 6. 48 см 2
Скачать презентацию Теорема о биссектрисе и медиане треугольника подготовил
Теорема о биссектрисе и медиане треугольника.ppt