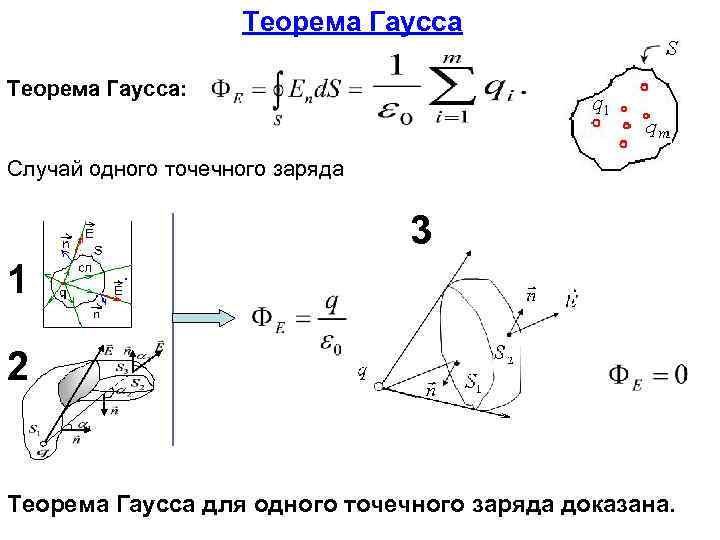
 Теорема Гаусса: Случай одного точечного заряда 3 1 2 Теорема Гаусса для одного точечного заряда доказана.
Теорема Гаусса: Случай одного точечного заряда 3 1 2 Теорема Гаусса для одного точечного заряда доказана.
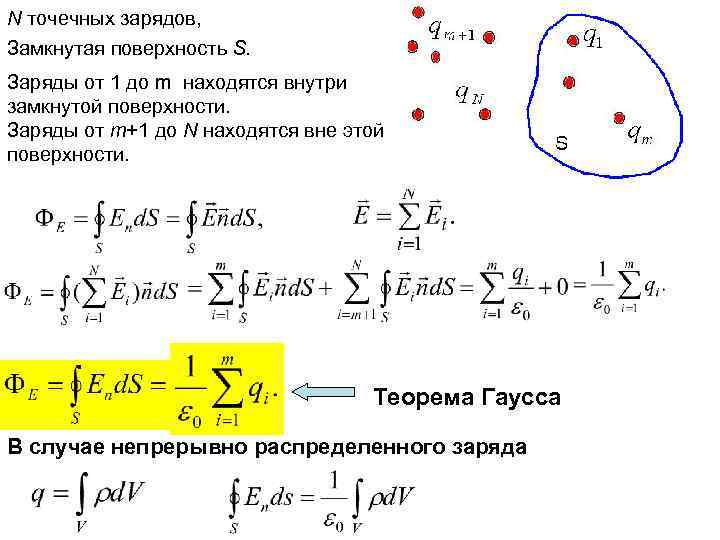 N точечных зарядов, Замкнутая поверхность S. Заряды от 1 до m находятся внутри замкнутой поверхности. Заряды от m+1 до N находятся вне этой поверхности. Теорема Гаусса В случае непрерывно распределенного заряда
N точечных зарядов, Замкнутая поверхность S. Заряды от 1 до m находятся внутри замкнутой поверхности. Заряды от m+1 до N находятся вне этой поверхности. Теорема Гаусса В случае непрерывно распределенного заряда
 РАСЧЕТ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ
РАСЧЕТ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ
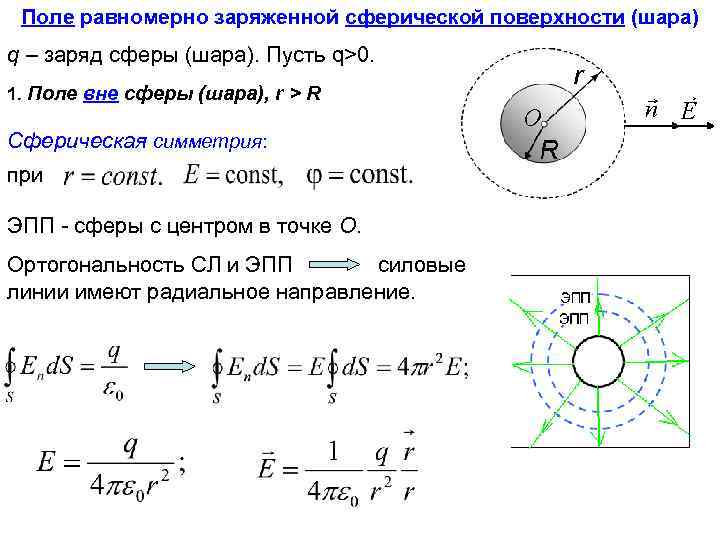 Поле равномерно заряженной сферической поверхности (шара) q – заряд сферы (шара). Пусть q>0. 1. Поле вне сферы (шара), r > R Сферическая симметрия: при ЭПП - сферы с центром в точке О. Ортогональность СЛ и ЭПП силовые линии имеют радиальное направление.
Поле равномерно заряженной сферической поверхности (шара) q – заряд сферы (шара). Пусть q>0. 1. Поле вне сферы (шара), r > R Сферическая симметрия: при ЭПП - сферы с центром в точке О. Ортогональность СЛ и ЭПП силовые линии имеют радиальное направление.
 Поле равномерно заряженной сферической поверхности (шара) Поле вне сферы (шара), r > R Сферическая симметрия – потенциал зависит только от r. Потенциальное поле - можно выбрать любую траекторию. Будем удалять пробный заряд в радиальном направлении.
Поле равномерно заряженной сферической поверхности (шара) Поле вне сферы (шара), r > R Сферическая симметрия – потенциал зависит только от r. Потенциальное поле - можно выбрать любую траекторию. Будем удалять пробный заряд в радиальном направлении.
 Поле равномерно заряженной сферической поверхности (шара) 2. Поле внутри сферы , r < R rR При r > R поле такое же как от точечного заряда, распложенного в центре сферы.
Поле равномерно заряженной сферической поверхности (шара) 2. Поле внутри сферы , r < R rR При r > R поле такое же как от точечного заряда, распложенного в центре сферы.
 Поле бесконечной равномерно заряженной плоскости Симметрия: при ЭПП - плоскости параллельные заряженной плоскости. Ортогональность СЛ и ЭПП силовые линии перпендикулярны заряженной плоскости Произвольная замкнутая поверхность: цилиндр, ось которого параллельна силовым линиям. Введём поверхностную плотность заряда однородное поле
Поле бесконечной равномерно заряженной плоскости Симметрия: при ЭПП - плоскости параллельные заряженной плоскости. Ортогональность СЛ и ЭПП силовые линии перпендикулярны заряженной плоскости Произвольная замкнутая поверхность: цилиндр, ось которого параллельна силовым линиям. Введём поверхностную плотность заряда однородное поле
 Поле бесконечной равномерно заряженной плоскости Распределение потенциала ЭПП - плоскости параллельные заряженной плоскости. Потенциал зависит только от х. Работа не зависит от траектории. Следовательно, для того чтобы найти потенциал в любом месте, достаточно найти работу по перемещению пробного заряда вдоль х. σ следует брать с учетом ее знака. 0
Поле бесконечной равномерно заряженной плоскости Распределение потенциала ЭПП - плоскости параллельные заряженной плоскости. Потенциал зависит только от х. Работа не зависит от траектории. Следовательно, для того чтобы найти потенциал в любом месте, достаточно найти работу по перемещению пробного заряда вдоль х. σ следует брать с учетом ее знака. 0
 Поле бесконечной равномерно заряженной плоскости не стремится к 0. Прочитано до сих. Следствие бесконечности заряженной плоскости Приближение бесконечной заряженной плоскости корректно на расстояниях много меньших линейных размеров плоскости. И наоборот, на расстояниях много больших размеров заряженной плоскости её поле приближается к полю точечного заряда.
Поле бесконечной равномерно заряженной плоскости не стремится к 0. Прочитано до сих. Следствие бесконечности заряженной плоскости Приближение бесконечной заряженной плоскости корректно на расстояниях много меньших линейных размеров плоскости. И наоборот, на расстояниях много больших размеров заряженной плоскости её поле приближается к полю точечного заряда.