Теорема Гаусса Электрическое поле можно рассчитать применяя суперпозиции

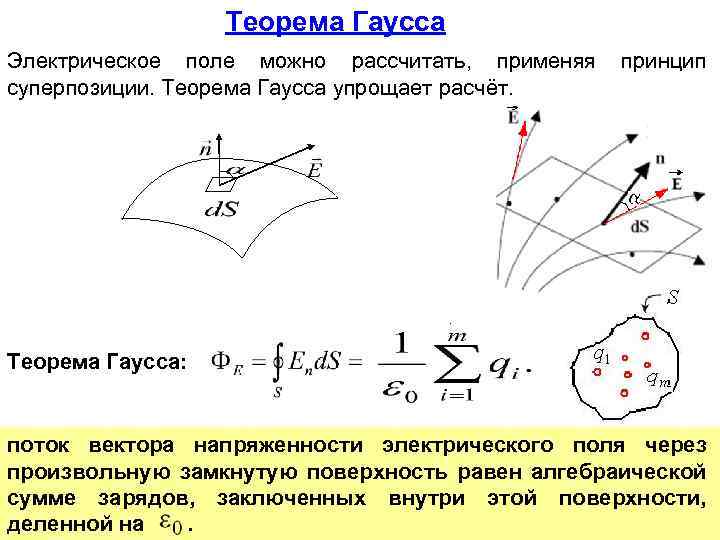Теорема Гаусса Электрическое поле можно рассчитать, применяя суперпозиции. Теорема Гаусса упрощает расчёт. принцип Теорема Гаусса: поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на.

РАСЧЕТ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ (продолжение)

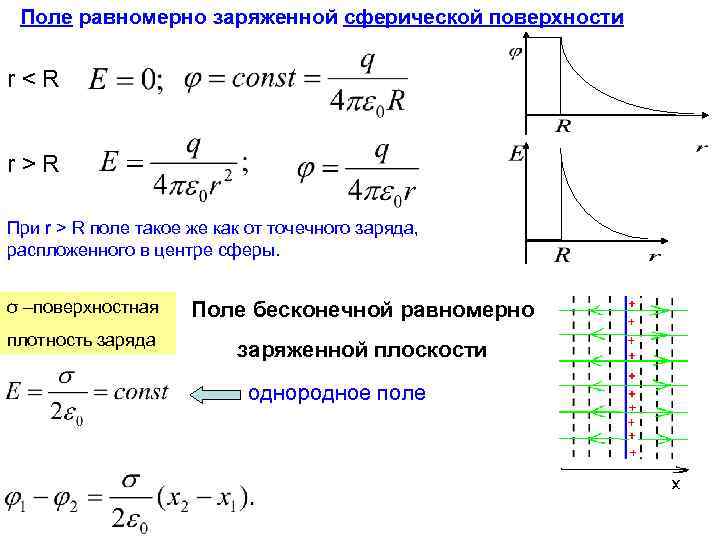Поле равномерно заряженной сферической поверхности rR При r > R поле такое же как от точечного заряда, распложенного в центре сферы. σ –поверхностная Поле бесконечной равномерно плотность заряда заряженной плоскости однородное поле

Поле двух параллельных равномерно разноименно заряженных бесконечных плоскостей Принцип суперпозиции: Области (1) и (3): Е=0 Область 2: Поле двух параллельных равномерно разноименно заряженных бесконечных плоскостей однородно и сосредоточено в пространстве между плоскостями.

Поле бесконечной равномерно заряженной цилиндрической поверхности - линейная плотность заряда Поле вне равномерно заряженной цилиндрической поверхности Симметрия: в точках, равноотстоящих от оси, свойства поля одинаковы. ЭПП - соосные цилиндрические поверхности. СЛ – ортогональны ЭПП, радиальны, перпендикулярны оси цилиндра. Произвольная замкнутая поверхность: соосная цилиндрическая поверхность.

Поле бесконечной равномерно заряженной цилиндрической поверхности Поле вне равномерно заряженной цилиндрической поверхности Поле внутри равномерно заряженной цилиндрической поверхности (r

Поле бесконечной равномерно заряженной цилиндрической поверхности не стремится к 0. Следствие бесконечности заряженного цилиндра

ЭЛЕКТРИЧЕСКИЙ ДИПОЛЬ q+=|q–|=q; l – плечо диполя, l << r Электрический момент диполя – векторная величина. Вектор направлен от минуса к плюсу и численно равен

Диполь в однородном электрическом поле На каждый заряд действует сила Пара сил – вращение. , Наиболее характерные положения диполя: положение устойчивого равновесия, положение неустойчивого равновесия, соответствует максимальной величине момента сил M.

Диполь в однородном электрическом поле Потенциальная энергия электрического диполя Работа при повороте диполя .

Электрический диполь в неоднородном электрическом поле В однородном поле на диполь действует момент сил угловое ускорение – ориентационный поворот ; сумма действующих сил = 0 В неоднородном поле ( поступательное ускорение = 0. ) появляется сила: После того как диполь повернулся и встал по полю El = E Сила направлена в сторону большего поля – диполь втягивается в область более сильного поля.

Электрический диполь в неоднородном электрическом поле В однородном поле на диполь действует момент сил угловое ускорение – ориентационный поворот ; сумма действующих сил = 0 В неоднородном поле ( поступательное ускорение = 0. ) появляется сила: После того как диполь повернулся и встал по полю El = E Сила направлена в сторону большего поля – диполь втягивается в область более сильного поля.

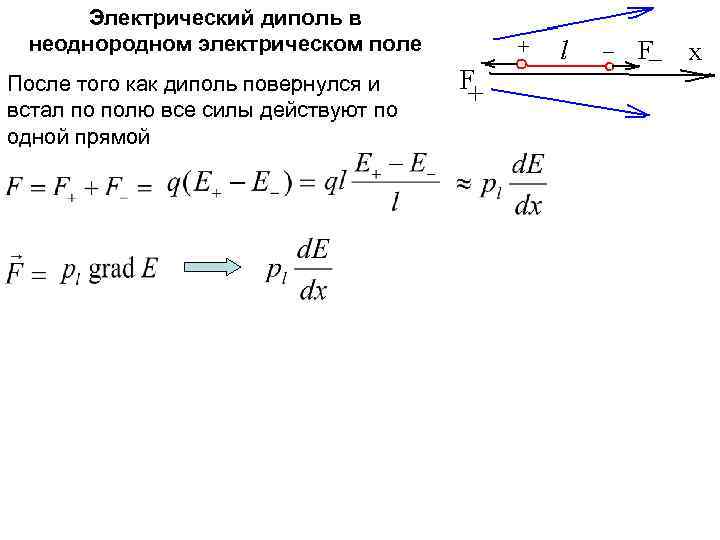Электрический диполь в неоднородном электрическом поле После того как диполь повернулся и встал по полю все силы действуют по одной прямой

Диэлектрики в электрическом поле Полярные и неполярные молекулы. Неполярные молекулы Заряды расположены симметрично, «центры» положительного и отрицательного зарядов совпадают. деформация молекулы, центры + и – не совпадают - индуцированный дипольный момент - поляризуемость, характеристика молекулы (м 3) Полярные молекулы Асимметричное распределение положительного и отрицательного зарядов ориентация по полю

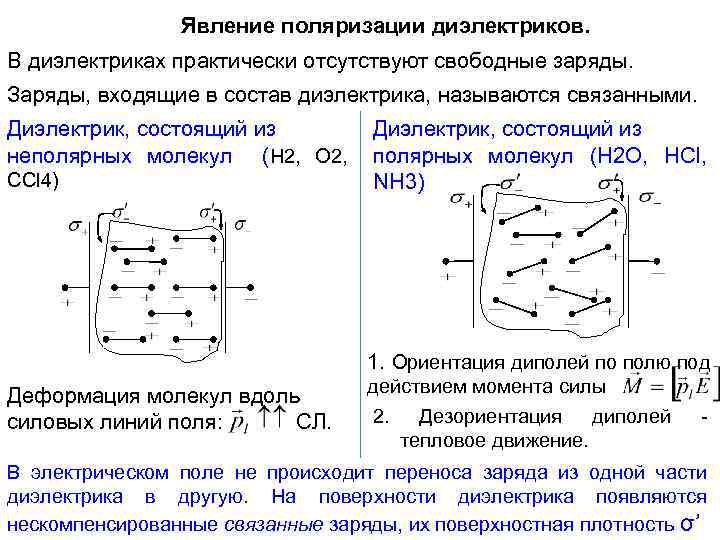Явление поляризации диэлектриков. В диэлектриках практически отсутствуют свободные заряды. Заряды, входящие в состав диэлектрика, называются связанными. Диэлектрик, состоящий из неполярных молекул (H 2, O 2, CCl 4) Диэлектрик, состоящий из полярных молекул (Н 2 О, HCl, NH 3) 1. Ориентация диполей по полю под Деформация молекул вдоль силовых линий поля: СЛ. действием момента силы 2. Дезориентация диполей тепловое движение. - В электрическом поле не происходит переноса заряда из одной части диэлектрика в другую. На поверхности диэлектрика появляются нескомпенсированные связанные заряды, их поверхностная плотность σ’

Явление поляризации диэлектриков. Поляризация → сумма электрических дипольных моментов молекул отлична от нуля. Вектор поляризации ( Кл/м 2): – физически малый объем; – электрический момент i-го диполя. Для неполярных молекул, которые все ориентированы по полю N – число молекул в объеме ; – дипольный момент молекулы; n – концентрация молекул. Неполярные молекулы: - диэлектрическая восприимчивость (безразмерная величина). Полярные молекулы (жёсткие диполи) – то же

Явление поляризации диэлектриков. Диэлектрики из неполярных молекул: не зависит от Т Диэлектрики из полярных молекул: Для ионных кристаллов (гигантская полярная молекула, например Na. Cl) не зависит от температуры. Материалы, для которых сегнетоэлектриками (для сегнетоэлектриков зависит от Е сильнее, чем линейно).

Характеристики электрического поля в диэлектрике - напряженность поля свободных зарядов, – напряженность поля связанных зарядов, – напряженность результирующего поля в диэлектрике. По принципу суперпозиции Вектор электрической индукции (Кл/м 2): диэлектрическая восприимчивость - диэлектрическая проницаемость (безразмерная) Для вакуума