163ad7c15395fa99f784ef0a7b33134b.ppt
- Количество слайдов: 17

Теорема Фалеса

• Устная работа • 1) Найдите угол между биссектрисами острых углов прямоугольного треугольника. • 2) Найдите углы между биссектрисами двух углов треугольника, если третий угол равен 40. • 3) Найдите углы между биссектрисами острых углов тупоугольного треугольника, если его тупой угол равен 130. • 4) Почему биссектрисы двух углов треугольника не могут быть параллельными? • 5) Определите вид треугольника, если одна из его медиан равна половине стороны, к которой она проведена. • 6) Найдите углы параллелограмма, если один угол составляет 80% другого. • 7) Найдите основания и среднюю линию трапеции, если одно основание составляет 40% от другого и меньше его на 24 см.

Практическая работа

• Изобразим угол AOB. На одной из его сторон, например OA, отложим равные отрезки, а именно, OA 1=A 1 A 2. • Через точки A 1 и A 2 проведем параллельные прямые таким образом, чтобы они пересекли вторую сторону данного угла, точки пересечения назовем соответственно B 1 и B 2. • Измерим отрезки OB 1 и B 1 B 2. На OA отложим отрезок A 2 A 3=A 1 A 2 и через точку A 3 проведем прямую, параллельную проведенным прямым, например A 2 B 2. • Точку пересечения с OB назовем B 3. • Измерим получившийся отрезок B 2 B 3. • Какое предположение можно сделать?
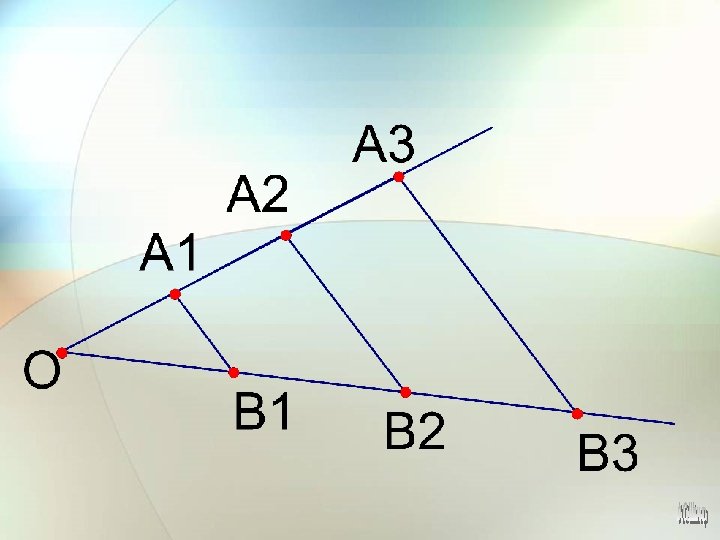

• Теорема. (Фалеса. ) Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

• Доказательство. Пусть А 1, А 2, А 3 – точки пересечения параллельных прямых с одной из сторон угла; • В 1, В 2, В 3 – соответствующие точки пересечения параллельных прямых с другой стороной угла • Если А 1 А 2=А 2 А 3, то А 2 В 2 – средняя линия трапеции А 1 А 3 В 3 В 1 • (следствие из теоремы о средней линии трапеции) и, • следова тельно, В 1 В 2 = В 2 В 3. ■
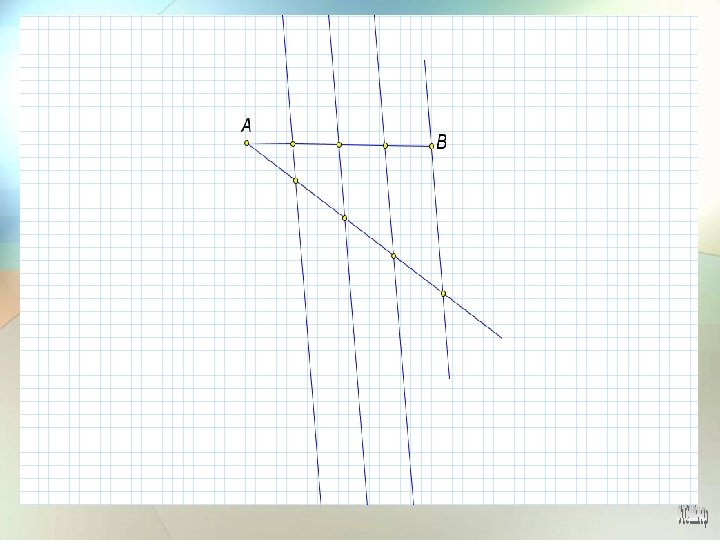
Задание Разделите отрезок АВ на 4 равные части

- Что означает запись и CD данные отрезки? , где AB Отношением двух отрезков AB и CD называется число, показывающее сколько раз отрезок CD и его части укладываются в отрезке АВ. Если отрезок CD принять за единичный, то отношение будет равно длине отрезка AB. Отношение отрезков AB и CD обозначается также AB: CD.

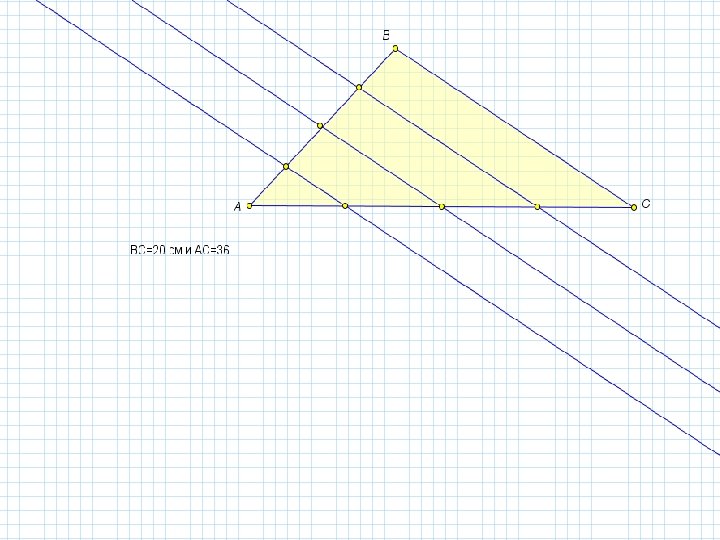
Решите задачи • 1. Разделите данный отрезок на 5 равных частей. • 2. Данный отрезок разделите на два отрезка, длины которых пропорциональны числам 1, 2. • 3. В треугольнике ABC стороны BC=20 см и AC=36 см. Сторона AB разделена на 4 равные части и через точки деления проведены прямые, параллельные стороне BC. Найдите отрезки этих прямых, заключенные внутри треугольника, и отрезки, полученные на стороне AC.
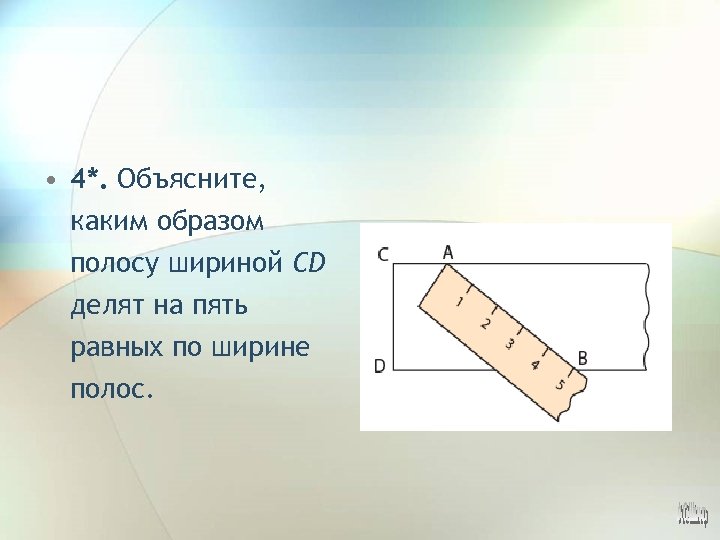
• 4*. Объясните, каким образом полосу шириной CD делят на пять равных по ширине полос.

V. Задание на дом • 1. Выучить разобранную на уроке теорию (п. 34 учебника). • 2. Решить задачи. • 1) Разделите данный отрезок на 6 равных частей. • 2) Данный отрезок разделите на два отрезка, длины которых пропорциональны числам 2, 3. • 3) Дан параллелограмм ABCD, точки E и F – середины его сторон соответственно BC и AD. Докажите, используя теорему Фалеса, что отрезки BF и DE делят диагональ AC на три равные части. • Указание. BEDF – параллелограмм, значит, BF||DE, нужно рассмотреть углы BCA и DAC.

• 3) Дан параллелограмм ABCD, точки E и F – середины его сторон соответственно BC и AD. Докажите, используя теорему Фалеса, что отрезки BF и DE делят диагональ AC на три равные части. • Указание. BEDF – параллелограмм, значит, BF||DE, нужно рассмотреть углы BCA и DAC.
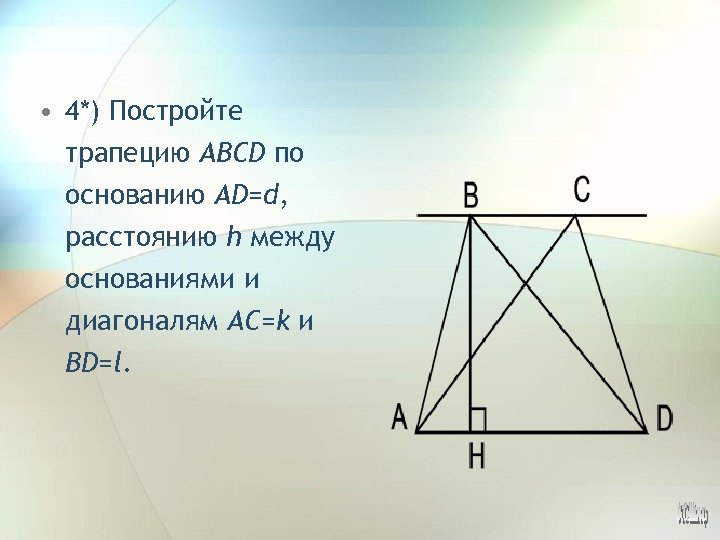
• 4*) Постройте трапецию ABCD по основанию AD=d, расстоянию h между основаниями и диагоналям AC=k и BD=l.

• 3*. Индивидуальное задание. Сообщение на тему «Жизнь и творчество Фалеса» . Литература: Учебник, параграф 34, раздел «Исторические сведения» ;

163ad7c15395fa99f784ef0a7b33134b.ppt