ТЕОРЕМА ЭЙЛЕРА ВЫПОЛНИЛА УЧЕНИЦА 10 КЛАССА В МАОУ

ТЕОРЕМА ЭЙЛЕРА ВЫПОЛНИЛА УЧЕНИЦА 10 КЛАССА В МАОУ «ЛИЦЕЙ № 3» СМИРНОВА ЮЛИЯ

ЛЕОНА РД Э ЙЛЕР - швейцарский, немецкий и российский математик и механик. Эйлер — автор более чем 850 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и другим областям.

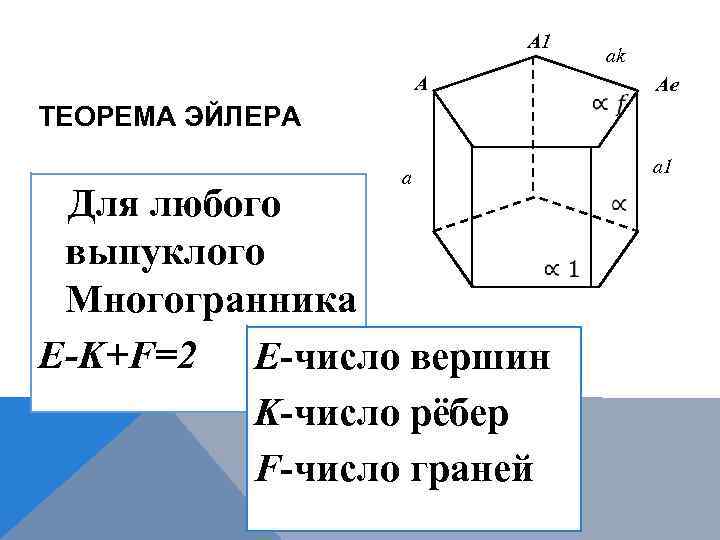A 1 A ТЕОРЕМА ЭЙЛЕРА ak Ae a 1 a Для любого выпуклого Многогранника E-K+F=2 E-число вершин K-число рёбер F-число граней

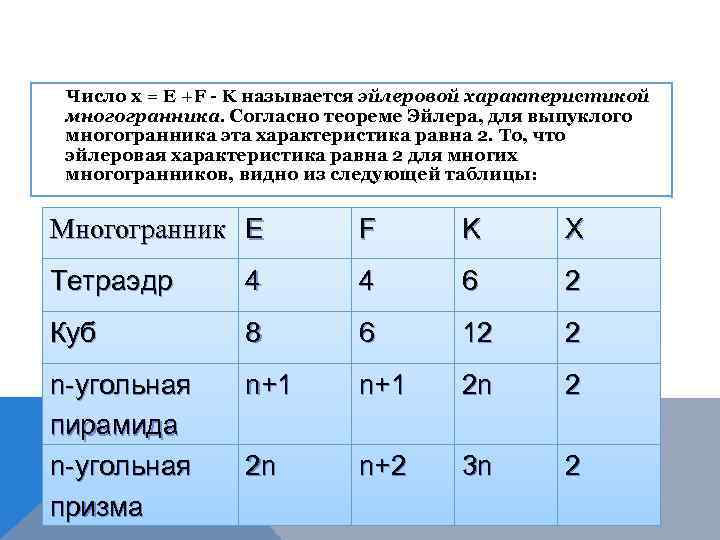Число х = E +F - K называется эйлеровой характеристикой многогранника. Согласно теореме Эйлера, для выпуклого многогранника эта характеристика равна 2. То, что эйлеровая характеристика равна 2 для многих многогранников, видно из следующей таблицы: Многогранник E F K X Тетраэдр 4 4 6 2 Куб 8 6 12 2 n-угольная пирамида n-угольная призма n+1 2 n 2 2 n n+2 3 n 2

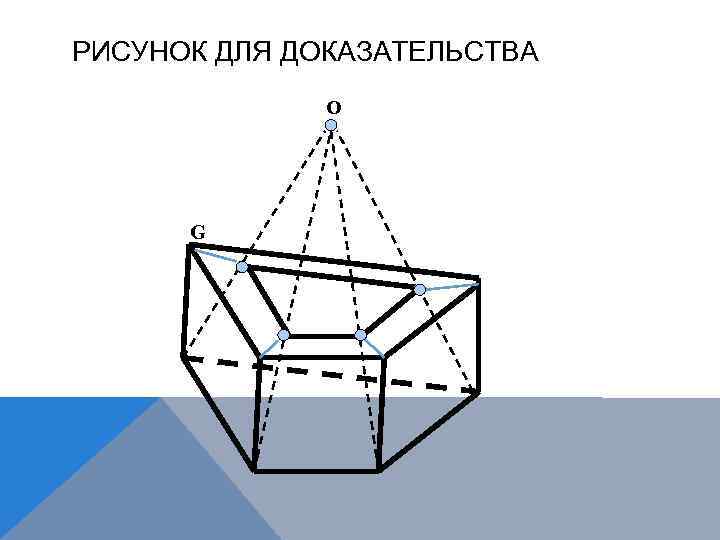РИСУНОК ДЛЯ ДОКАЗАТЕЛЬСТВА O G

ДОКАЗАТЕЛЬСТВО. Возьмем снаружи многогранника точку О вблизи от какой-либо грани G и спроектируем остальные грани на G из центра О. Их проекции образуют разбиение грани G на многоугольники. Подсчитаем двумя способами сумму α углов всех полученных многоугольников и самой грани G. Сумма углов n-угольника равна π(n - 2). Сложим эти числа для всех граней (включая грань G). Сумма членов вида πn равна общему числу сторон всех граней, т. е. 2 K- ведь каждое из K рёбер принадлежит двум граням. А так как у нас всего F слагаемых, α = π(2 K – 2 F).

ДОКАЗАТЕЛЬСТВО. Теперь найдем сумму углов при каждой вершине разбиения и сложим эти суммы. Если вершина лежит внутри грани G, то сумма углов вокруг нее равна 2π. Таких вершин E-m, где m- число вершин самой грани G, а значит, их вклад равен 2π(E - m). Углы при вершинах G считаются в сумме дважды (как углы G и как углы многоугольников разбиения); их вклад равен 2π(m - 2). Таким образом, α = 2π(E m) + 2π(m - 2) = 2π(E - 2). Приравнивая два результата и сокращения на 2π, получаем требуемое равенство K - F = E - 2

СПАСИБО ЗА ВНИМАНИЕ