Скачать презентацию ТЕМА ВВЕДЕНИЕ В ТЕОРИЮ ГРАФОВ ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
Презентация 37_ОАиП.ppt
- Количество слайдов: 9
ТЕМА: ВВЕДЕНИЕ В ТЕОРИЮ ГРАФОВ.
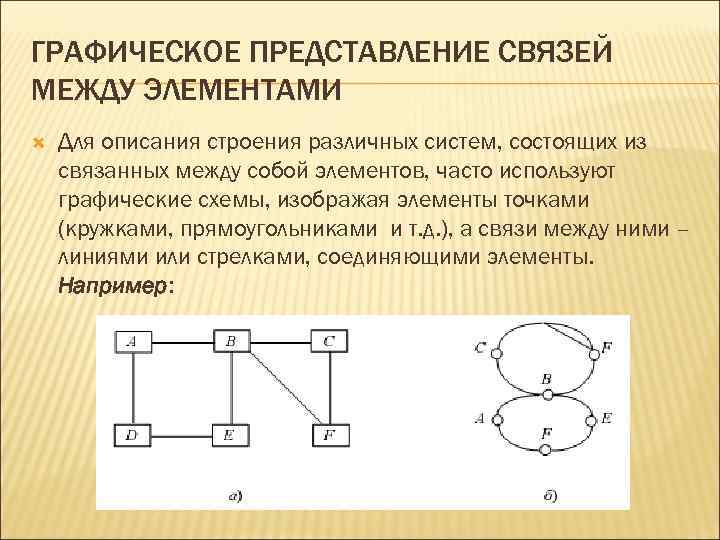ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СВЯЗЕЙ МЕЖДУ ЭЛЕМЕНТАМИ Для описания строения различных систем, состоящих из связанных между собой элементов, часто используют графические схемы, изображая элементы точками (кружками, прямоугольниками и т. д. ), а связи между ними – линиями или стрелками, соединяющими элементы. Например:
На таких диаграммах важно лишь, какие именно пары элементов соединены линиями. На рисунке изображена одна и та же структура связей между элементами A, B, C, D, E, F. Пары связанных между собой элементов - (A, B), (A, D), (B, C), (B, E), (D, E), (C, F), (B, F). Есть два списка: список элементов и список пар элементов. Все они составляют понятие, которое математики называют графом. Граф - совокупность точек и линий, в которой каждая линия соединяет две точки. Точки называются вершинами (узлами) графа, линии - ребрами графа.
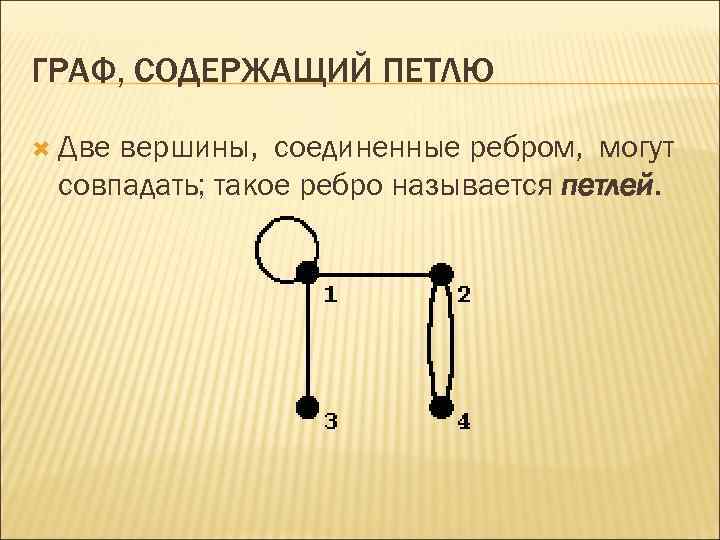ГРАФ, СОДЕРЖАЩИЙ ПЕТЛЮ Две вершины, соединенные ребром, могут совпадать; такое ребро называется петлей.
Граф состоит из двух множеств – множества вершин и множества ребер, причем для каждого ребра указана пара вершин, которые это ребро соединяет. Вершины и ребра называются элементами графа. Если ребро соединят две вершины, то говорят, что оно им инцидентно; вершины, соединенные ребром называются смежными.
ОРИЕНТИРОВАННЫЙ ИЛИ НЕОРИЕНТИРОВАННЫЙ ГРАФ: Если порядок элементов в паре важен, то мы имеем упорядоченные пары, и ребро называется ориентированным, если порядок элементов в паре не важен, то мы имеем неупорядоченные пары, и ребро называется неориентированным. Чаще всего графы содержат один тип ребер, в соответствии с которым и весь граф называют ориентированным или неориентированным. Для неориентированного ребра порядок, в котором указанны соединяемые им вершины, не важен. Для ориентированного ребра важно: первой указывается вершина, из которой выходит ребро.
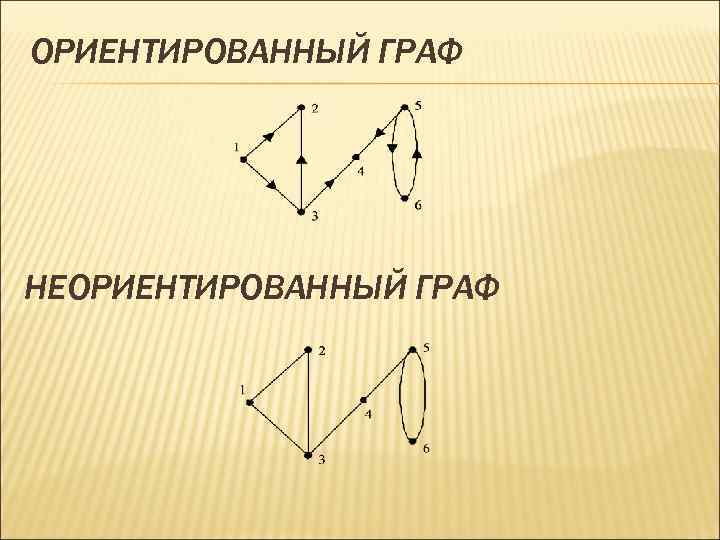ОРИЕНТИРОВАННЫЙ ГРАФ НЕОРИЕНТИРОВАННЫЙ ГРАФ
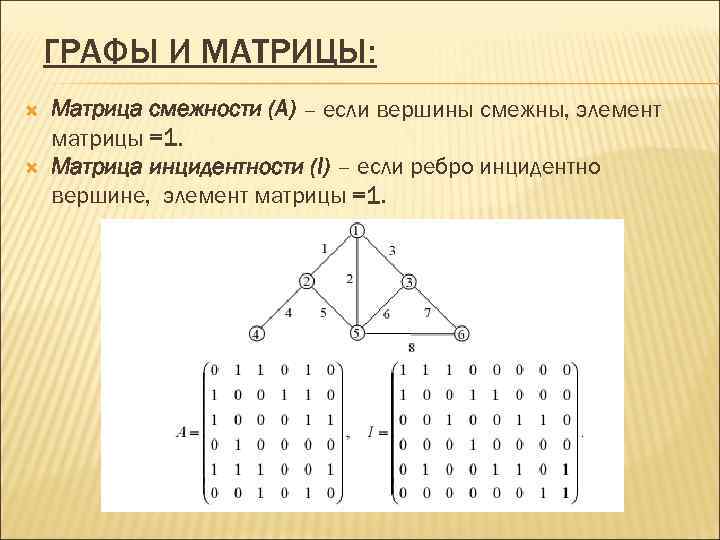ГРАФЫ И МАТРИЦЫ: Матрица смежности (A) – если вершины смежны, элемент матрицы =1. Матрица инцидентности (I) – если ребро инцидентно вершине, элемент матрицы =1.
ПРИМЕР: ПОСТРОИТЬ МАТРИЦЫ СМЕЖНОСТИ И ИНЦИДЕНТНОСТИ.