ТЕМА ВОЛНОВОЕ ДВИЖЕНИЕ 1 Образование волн

Зарегистрируйтесь, чтобы просмотреть полный документ!

ТЕМА: ВОЛНОВОЕ ДВИЖЕНИЕ

§ 1. Образование волн. Классификация волн Колебательное движение подразумевало колебание тела (груза) или материальной точки. Волновое движение включает процессы распространения колебаний материальных частиц в упругой среде. Это обусловлено взаимосвязью частиц среды друг с другом. Законы, определяющие эту связь, подобны законам упругих сил. Процесс распространения колебаний в упругой среде называется волновым движением, а распространяющееся в среде периодическое возмущение – Волной. Частицы среды не перемещаются с волной, а колеблются около своих положений равновесия. Волны классифицируются по разным параметрам: а) по геометрическим параметрам – одномерная, двухмерная, трехмерная волна; б) по ориентации направления колебаний отдельных частиц среды и направления распространения самой волны

Различают: 1) продольные 2) поперечные волны. 1) Продольная волна – если частицы колеблются в том же направлении, в котором распространяются колебания (направление волны). Пример: звуковая волна. частица 2) Поперечная волна – если частицы колеблются перпендикулярно к направлению распространения волны. частица - Этот характер волны обусловлен упругими свойствами среды. В газах и жидкостях могут быть продольные волны, т. к. в них отсутствует сопротивление упругой деформации. Наоборот, в случае твердых тел, обладающих сопротивлением сдвигу, могут возникать поперечные волны. В этом случае сдвиг слоев вызывает волну, перпендикулярную смещению частиц.

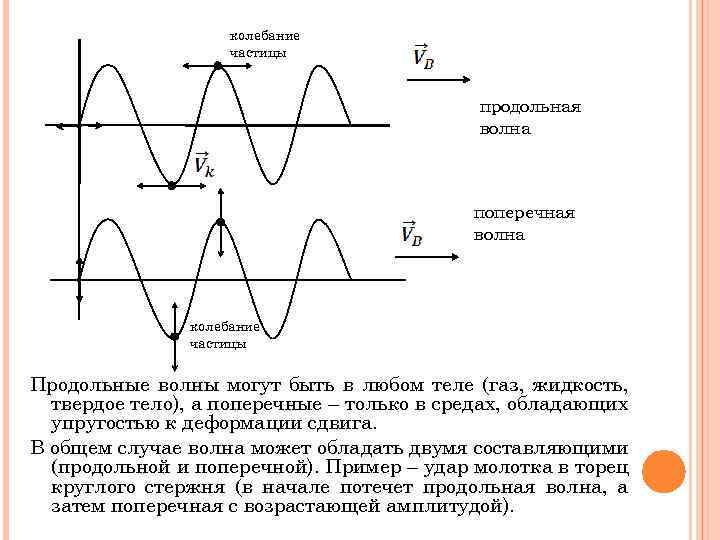
колебание частицы продольная волна поперечная волна колебание частицы Продольные волны могут быть в любом теле (газ, жидкость, твердое тело), а поперечные – только в средах, обладающих упругостью к деформации сдвига. В общем случае волна может обладать двумя составляющими (продольной и поперечной). Пример – удар молотка в торец круглого стержня (в начале потечет продольная волна, а затем поперечная с возрастающей амплитудой).

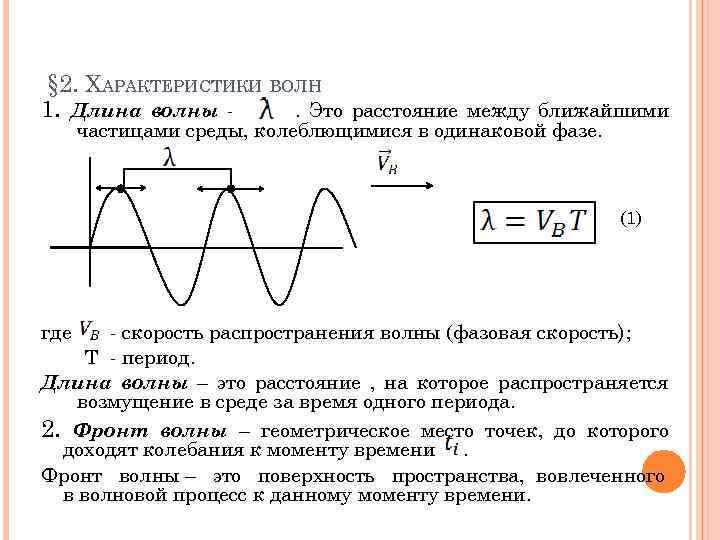
§ 2. ХАРАКТЕРИСТИКИ ВОЛН 1. Длина волны. Это расстояние между ближайшими частицами среды, колеблющимися в одинаковой фазе. (1) где - скорость распространения волны (фазовая скорость); T - период. Длина волны – это расстояние , на которое распространяется возмущение в среде за время одного периода. 2. Фронт волны – геометрическое место точек, до которого доходят колебания к моменту времени. Фронт волны – это поверхность пространства, вовлеченного в волновой процесс к данному моменту времени.

3. Волновая поверхность – геометрическое место точек, колеблющихся в одинаковой фазе. Волновую поверхность можно провести через любую точку пространства, охваченную волновым процессом. То есть волновых поверхностей множество, а волновой фронт один в каждый момент времени. Волновые поверхности неподвижны, а волновой фронт все время перемещается. В зависимости от формы фронта волны бывают сферические, плоские, эллипсовидные. В изотропных средах ( во всех направлениях) для трехмерного пространства фронт - сфера, волна сферическая. В дали от источника небольшие участки сферы можно принять за плоскость, а волну - плоской. В анизотропных средах ( в разных направлениях) фронт имеет форму эллипса. Волна эллипсовидная.

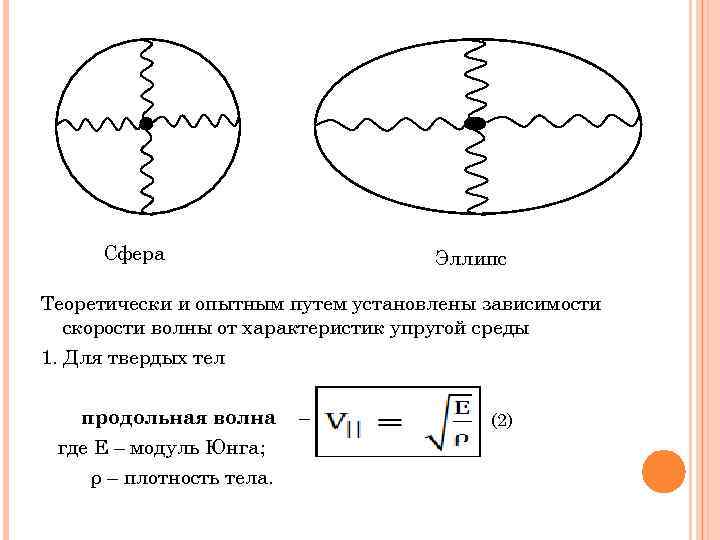
Сфера Эллипс Теоретически и опытным путем установлены зависимости скорости волны от характеристик упругой среды 1. Для твердых тел продольная волна где Е – модуль Юнга; ρ – плотность тела. – (2)

поперечная волна – (3) где G – модуль сдвига; ρ – плотность тела. 2. Для газа и жидкости продольная волна – (4) где K – модуль объемной упругости среды ( , - показатель адиабаты; P – давление) ρ – плотность среды.

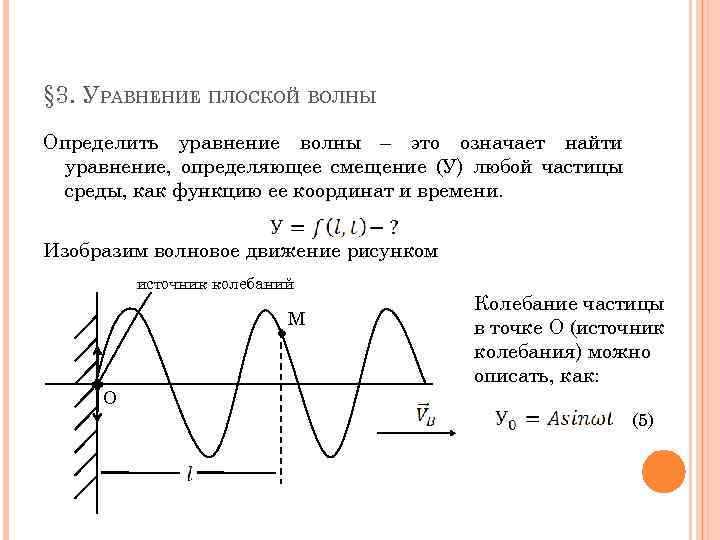
§ 3. УРАВНЕНИЕ ПЛОСКОЙ ВОЛНЫ Определить уравнение волны – это означает найти уравнение, определяющее смещение (У) любой частицы среды, как функцию ее координат и времени. Изобразим волновое движение рисунком источник колебаний М O Колебание частицы в точке О (источник колебания) можно описать, как: (5)

Колебание частицы в точке М, отстоящей от точки О на расстояние - , можно описать, как: (6) Время время задержки – колебания в точке М , где Получаем уравнение вида: или (7) это уравнение бегущей волны Если учесть, что в таком виде: , то уравнение (7) можно записать

Заменяя , получим: (8) Выражения (7) и (8) представляют уравнения плоской бегущей волны, распространяющейся вдоль. Аргумент Sin в уравнении зависит от двух переменных: времени – t и координаты. Таким образом, волна имеет двойную периодичность – в пространстве и во времени. Величина – const для данной частицы и представляет собой начальную фазу колебаний данной частицы (9)

§ 4. ПРИНЦИП СУПЕРПОЗИЦИИ. ИНТЕРФЕРЕНЦИЯ ВОЛН. Волновому движению присущ „Принцип суперпозиции” принцип независимости волн. Этот принцип определяется двумя признаками: 1) волны складываются геометрически; 2) волны, накладываясь, не искажают друга. Частный случай суперпозиции – явление интерференции. Это возможно, если частоты складываемых волн одинаковы и разность фаз постоянна или равна нулю. Такие волны называются когерентными. Рассмотрим два предельных случая сложения когерентных волн одного направления двух

(10) (11) Амплитуда результирующего колебания равна: (12) Разность фаз: (13)

Следовательно амплитуда результирующего колебания, согласно (12) и (13), будет определяться разностью хода . Если в будет укладываться целое число волн (или четное число полуволн), то результирующая амплитуда будет иметь max (14) при , k=0, 1, 2, 3… Если в будет укладываться нечетное число полуволн, то амплитуда будет – min при , k=0, 1, 2, 3… Эти заключения следуют из анализа выражения (12). (15)

Скачать презентацию ТЕМА ВОЛНОВОЕ ДВИЖЕНИЕ 1 Образование волн

6 5Волновое движение.pptx

Количество слайдов: 14