Тема уроку: Періодичність тригонометричних функцій. Побудова графіків тригонометричних







22_period.ppt
- Размер: 757.5 Кб
- Количество слайдов: 8
Описание презентации Тема уроку: Періодичність тригонометричних функцій. Побудова графіків тригонометричних по слайдам
 Тема уроку: Періодичність тригонометричних функцій. Побудова графіків тригонометричних функцій
Тема уроку: Періодичність тригонометричних функцій. Побудова графіків тригонометричних функцій
 Пригадаємо… 0 0 30 0 45 0 60 0 90 0 120 0 135 0 150 0 180 0 π 6 π 4 π 3 π 2 2 π 3 3 π 4 5 π 6 π
Пригадаємо… 0 0 30 0 45 0 60 0 90 0 120 0 135 0 150 0 180 0 π 6 π 4 π 3 π 2 2 π 3 3 π 4 5 π 6 π
 Подумайте Що спільного між кутами: — 33 0 0 390 0 750 0 1140 0 -6 9 0 0 = 30 0 — 1∙ 360 0= 30 0 -2∙ 360 0 = 30 0 +0∙ 360 0 = 30 0 +1∙ 360 0 = 30 0 +2∙ 360 0 = 30 0 +3∙ 360 0 30 0 -330 0 -690 0 390 0 750 0 1140 0 …О ХY π 6 +2 π ∙ 1 π 6 +2 π ∙ 2 π 6 +2 π ∙ 3π 6 +2 π ∙ 0π 6 +2 π ∙(-1)π 6 +2 π ∙(-2) Вся множина цих кутів записується так: Важливо! π 6 +2 π ∙ n, n є Z Z – множина ц ілих чисел (1, 2, 3, … 0, -1, -2, -3…) Зверніть увагу: sin (-6 9 0 0 )=sin (- 33 0 0 )=sin 30 0 =sin 390 0 =sin 750 0 =sin 1440 0 … cos (-6 9 0 0 )=cos (- 33 0 0 )=cos 30 0 =cos 390 0 =cos 750 0 =cos 1440 0 … 360 0 = 2 π
Подумайте Що спільного між кутами: — 33 0 0 390 0 750 0 1140 0 -6 9 0 0 = 30 0 — 1∙ 360 0= 30 0 -2∙ 360 0 = 30 0 +0∙ 360 0 = 30 0 +1∙ 360 0 = 30 0 +2∙ 360 0 = 30 0 +3∙ 360 0 30 0 -330 0 -690 0 390 0 750 0 1140 0 …О ХY π 6 +2 π ∙ 1 π 6 +2 π ∙ 2 π 6 +2 π ∙ 3π 6 +2 π ∙ 0π 6 +2 π ∙(-1)π 6 +2 π ∙(-2) Вся множина цих кутів записується так: Важливо! π 6 +2 π ∙ n, n є Z Z – множина ц ілих чисел (1, 2, 3, … 0, -1, -2, -3…) Зверніть увагу: sin (-6 9 0 0 )=sin (- 33 0 0 )=sin 30 0 =sin 390 0 =sin 750 0 =sin 1440 0 … cos (-6 9 0 0 )=cos (- 33 0 0 )=cos 30 0 =cos 390 0 =cos 750 0 =cos 1440 0 … 360 0 = 2 π
 Періоди функцій Для будь-якого кута α : 1) sin α = sin( α + 2 π ) 2 ) cos α = cos( α + 2 π ) 3 ) tg α = tg( α + π ) 4 ) ctg α = ctg( α + π ) Говорять, що функції сінус і косинус періодичні з періодом 2 π (або 360 0 ), функції тангенс і котангенс періодичні з періодом π (або 180 0 ) Розуміння поняття періодичності Припустимо, ми обчислили значення синусів усіх кутів від 0 до 359 0 і склали таблицю: Кут α sin α … і т. д. … 0 0 0 1 0 … 2 0 … 359 0 … … і т. д… 360 0 361 0 362 0 719 0 720 0 721 0 722 0 1079 0… і т. д… -360 0 -359 0 -358 0 … і т. д…
Періоди функцій Для будь-якого кута α : 1) sin α = sin( α + 2 π ) 2 ) cos α = cos( α + 2 π ) 3 ) tg α = tg( α + π ) 4 ) ctg α = ctg( α + π ) Говорять, що функції сінус і косинус періодичні з періодом 2 π (або 360 0 ), функції тангенс і котангенс періодичні з періодом π (або 180 0 ) Розуміння поняття періодичності Припустимо, ми обчислили значення синусів усіх кутів від 0 до 359 0 і склали таблицю: Кут α sin α … і т. д. … 0 0 0 1 0 … 2 0 … 359 0 … … і т. д… 360 0 361 0 362 0 719 0 720 0 721 0 722 0 1079 0… і т. д… -360 0 -359 0 -358 0 … і т. д…
 Правила знаходження періодів функцій Сінус або косинус Тангенс або котангенс Знайти період функції y = sin ( x + ) π 4 не звертаємо увагих = 2 π T Відповідь: T = 2 π. Знайти період функції y = sin (2 x — ) π 3 не звертаємо увагих = 2 πT 2 T = π Відповідь: T = π. Знайдіть періоди функцій: Самостійно a) y = sin(4 x + ); б) y = cos 2 x. π 6 Знайти період функції y = tg ( x + ) π 4 не звертаємо увагих = π T Відповідь: T = π. Знайти період функції y = ctg (2 x — ) π 3 не звертаємо увагих = πT 2 T = . π 2 Відповідь: T = π 2 Знайдіть періоди функцій: Самостійно a) y = ctg(4 x + ); б) y = tg 2 x. π
Правила знаходження періодів функцій Сінус або косинус Тангенс або котангенс Знайти період функції y = sin ( x + ) π 4 не звертаємо увагих = 2 π T Відповідь: T = 2 π. Знайти період функції y = sin (2 x — ) π 3 не звертаємо увагих = 2 πT 2 T = π Відповідь: T = π. Знайдіть періоди функцій: Самостійно a) y = sin(4 x + ); б) y = cos 2 x. π 6 Знайти період функції y = tg ( x + ) π 4 не звертаємо увагих = π T Відповідь: T = π. Знайти період функції y = ctg (2 x — ) π 3 не звертаємо увагих = πT 2 T = . π 2 Відповідь: T = π 2 Знайдіть періоди функцій: Самостійно a) y = ctg(4 x + ); б) y = tg 2 x. π
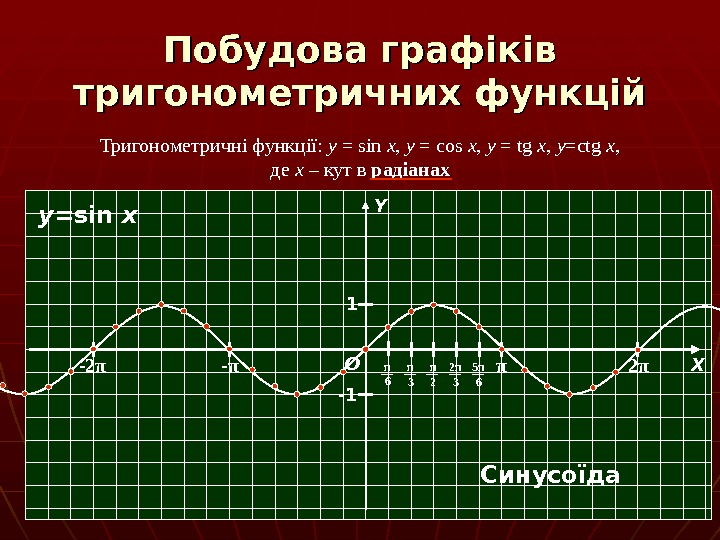
 Побудова графіків тригонометричних функцій Тригонометричні функції: y = sin x , y = cos x , y = tg x , y =ctg x , де х – кут в радіанах π 2 π — π-2 π О ХY π 6 π 3 π 2 2 π 3 5 π 61 -1 y =sin x Синусоїда
Побудова графіків тригонометричних функцій Тригонометричні функції: y = sin x , y = cos x , y = tg x , y =ctg x , де х – кут в радіанах π 2 π — π-2 π О ХY π 6 π 3 π 2 2 π 3 5 π 61 -1 y =sin x Синусоїда
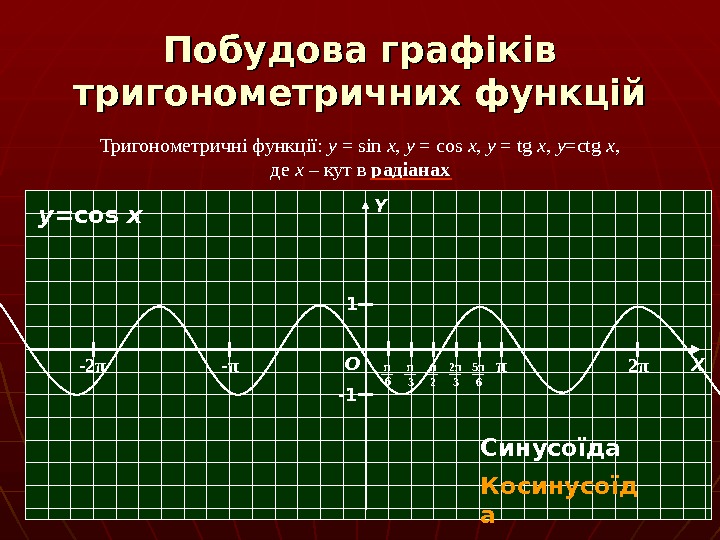
 Побудова графіків тригонометричних функцій Тригонометричні функції: y = sin x , y = cos x , y = tg x , y =ctg x , де х – кут в радіанах π 2 π — π-2 π О ХY π 6 π 3 π 2 2 π 3 5 π 61 -1 y =cos x Синусоїда Косинусоїд а
Побудова графіків тригонометричних функцій Тригонометричні функції: y = sin x , y = cos x , y = tg x , y =ctg x , де х – кут в радіанах π 2 π — π-2 π О ХY π 6 π 3 π 2 2 π 3 5 π 61 -1 y =cos x Синусоїда Косинусоїд а
 Домашнє завдання 1. 1. Знайти періоди функцій: yy = sin 3 xx ; yy = cos (3 — xx ); yy = tg ( xx ++ ππ )) 2. 2. Побудувати графіки функцій: yy = sin xx ++ 2; 2; yy = cos x x – 1– 1 3. 3. Повторити значення синусів, косинусів, тангенсів від 0 до
Домашнє завдання 1. 1. Знайти періоди функцій: yy = sin 3 xx ; yy = cos (3 — xx ); yy = tg ( xx ++ ππ )) 2. 2. Побудувати графіки функцій: yy = sin xx ++ 2; 2; yy = cos x x – 1– 1 3. 3. Повторити значення синусів, косинусів, тангенсів від 0 до

