Тема урока Смежные и вертикальные углы n

Тема урока: Смежные и вертикальные углы.

n n n Цели урока: Ознакомить учащихся с понятиями смежных и вертикальных углов, рассмотреть их свойства; Научить строить угол, смежный с данным углом, изображать вертикальные углы, находить на рисунке вертикальные и смежные углы.

Давай вспомним! n Что такое угол?

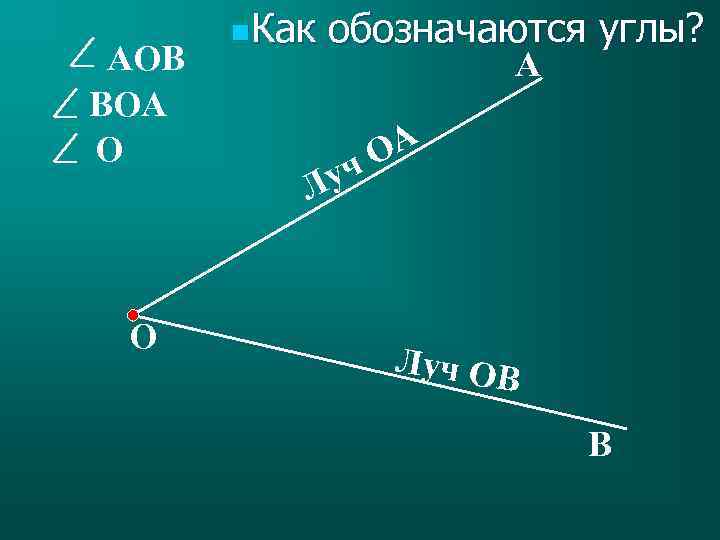АОВ ВОА О О n. Как обозначаются углы? А ОА ч Лу Луч ОВ В

Какой инструмент Для измерения можно углов использовать для используют измерения углов? транспортир. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

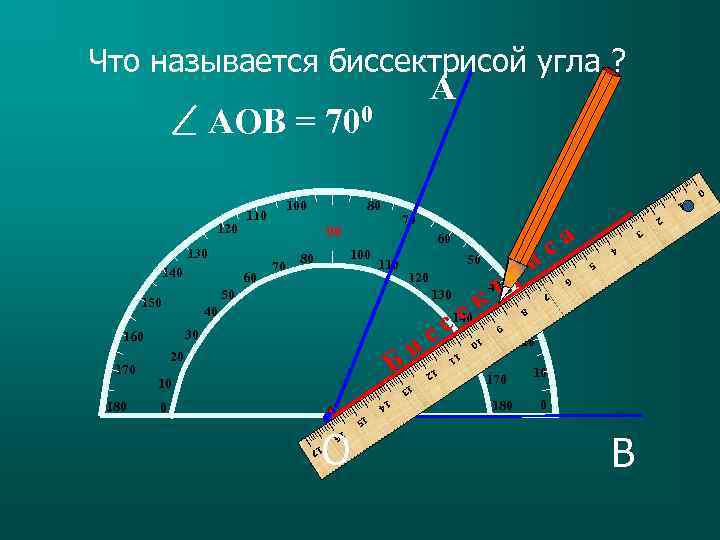IIIII 2 IIIII 3 B 0 10 20 8 7 6 5 4 IIIII IIIII IIIII 10 9 IIIII 11 IIIII 12 IIIII 13 IIIII 50 1 180 170 150 160 30 тр к 40 120 14 IIIII 110 са и IIIII 15 IIIII 16 IIIII 17 IIIII I Б ис се 140 130 80 70 80 IIIII O 0 10 20 30 70 100 60 90 100 0 180 170 160 40 150 50 60 140 130 120 110 АOB = 700 А Что называется биссектрисой угла ?

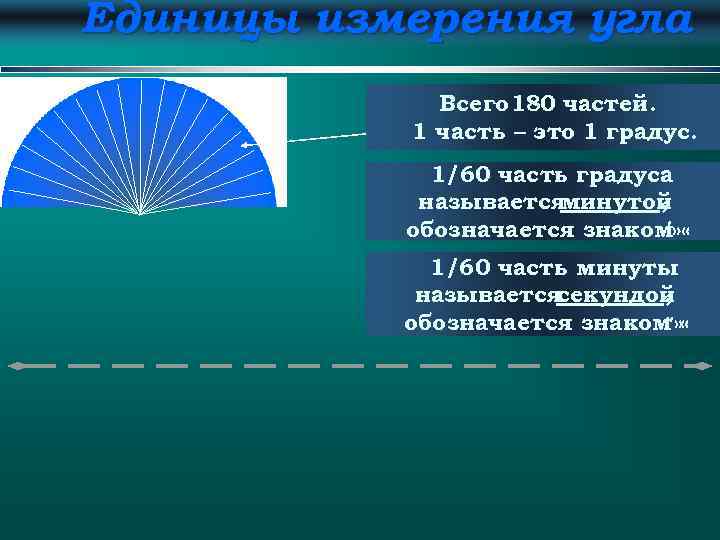Единицы измерения угла Всего 180 частей. 1 часть – это 1 градус. 1/60 часть градуса называется минутой , обозначается знаком « ′» 1/60 часть минуты называется секундой , обозначается знаком » « ″

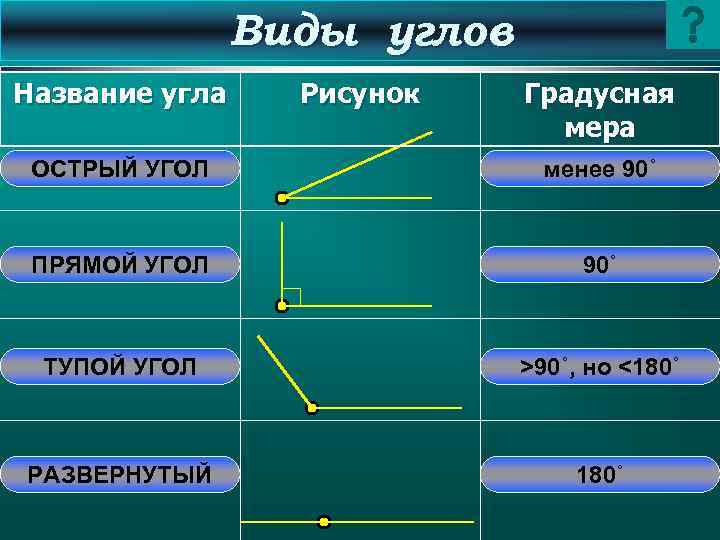Виды углов Название угла Рисунок Градусная мера ОСТРЫЙ УГОЛ менее 90˚ ПРЯМОЙ УГОЛ 90˚ ТУПОЙ УГОЛ >90˚, но <180˚ РАЗВЕРНУТЫЙ 180˚

n. К вашим знаниям об углах сегодня добавится еще два вида:

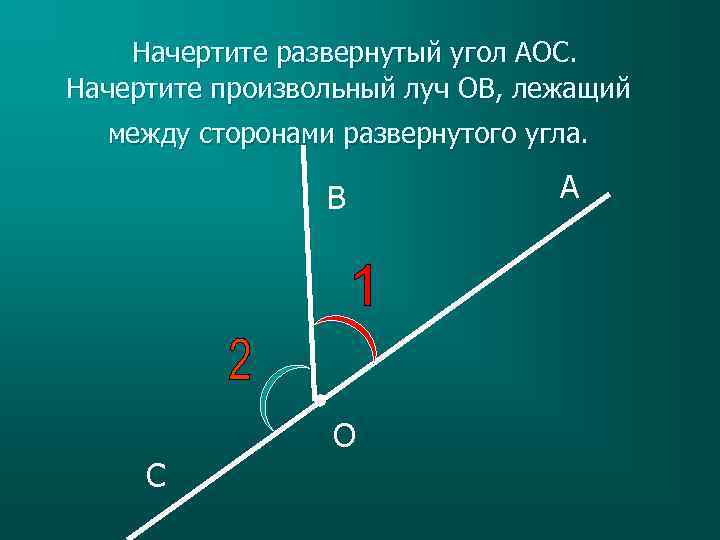Начертите развернутый угол АОС. Начертите произвольный луч ОB, лежащий между сторонами развернутого угла. B O C A

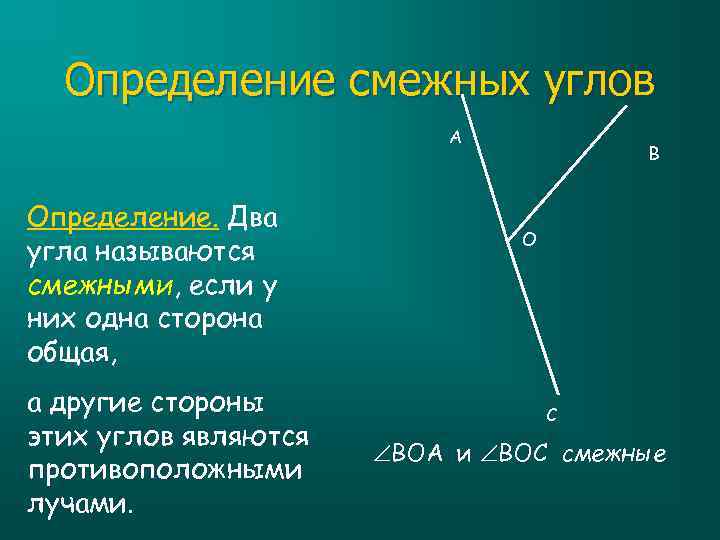Определение смежных углов А а другие стороны этих углов являются противоположными лучами. О О О О Определение. Два угла называются смежными, если у них одна сторона общая, В С ВОА и ВОС смежные

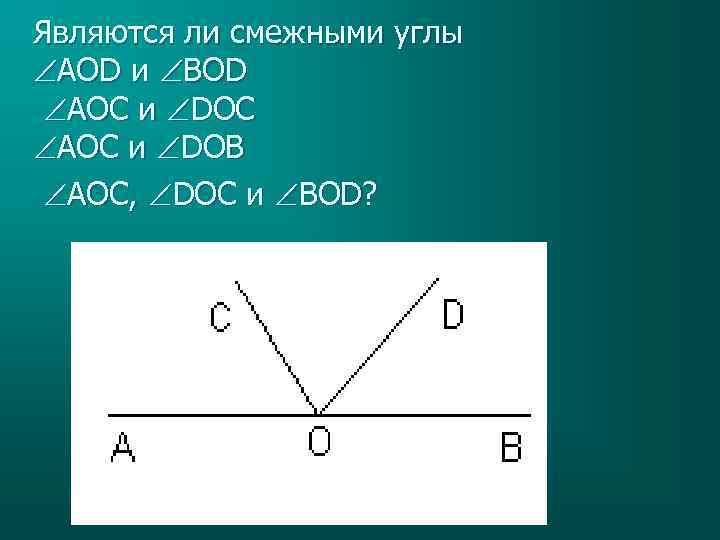Являются ли смежными углы AOD и BOD AOС и DOС AOС и DOВ AOС, DOС и BOD?

Построение смежных углов

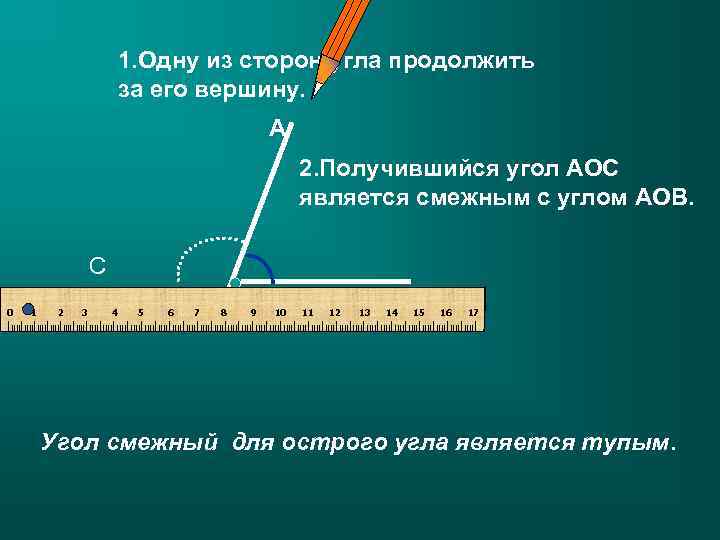1. Одну из сторон угла продолжить за его вершину. А 2. Получившийся угол АОС является смежным с углом АОВ. С 0 1 2 3 4 5 6 7 8 О 9 10 11 12 13 14 В 15 16 17 IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII Угол смежный для острого угла является тупым.

1. Одну из сторон угла продолжить за его вершину. А С О В 2. Получившийся угол АОС является смежным для угла АОВ. Угол смежный для тупого угла является острым.

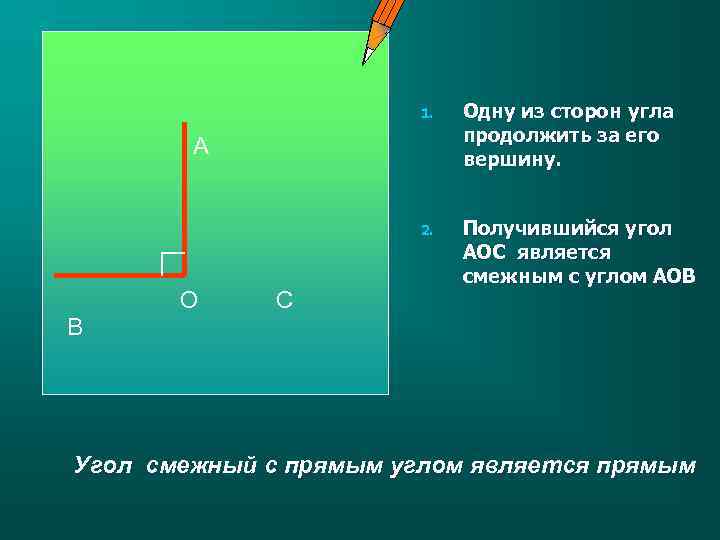1. Одну из сторон угла продолжить за его вершину. 2. Получившийся угол АОС является смежным с углом АОВ А В О С Угол смежный с прямым углом является прямым

Cвойство смежных углов Теорема. Сумма смежных углов С B A О 1. Сколько углов изображено на рисунке? Какие это углы? 2. Существует ли какая-нибудь взаимосвязь между этими углами? (Вспомните аксиому сложения углов). равна 1800 Дано: AOC и BOC – смежные. Доказать: AOC + BOC = 180. Доказательство. 1) Так как AOC и BOC – смежные, то лучи ОА и ОВ – противоположные, то есть, AOB – развернутый, следовательно, AOB = 180. 2) Луч OC проходит между сторонами AOB, значит, AOC + BOC = AOB = 180

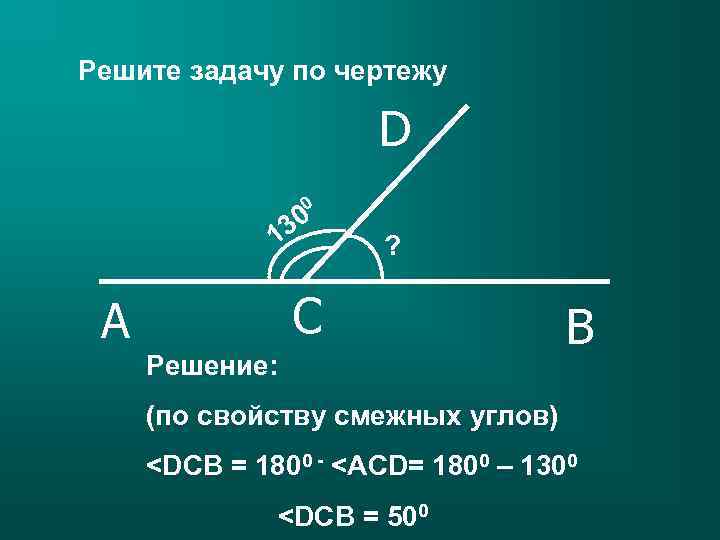Решите задачу по чертежу D 0 30 1 ? C A Решение: B (по свойству смежных углов)

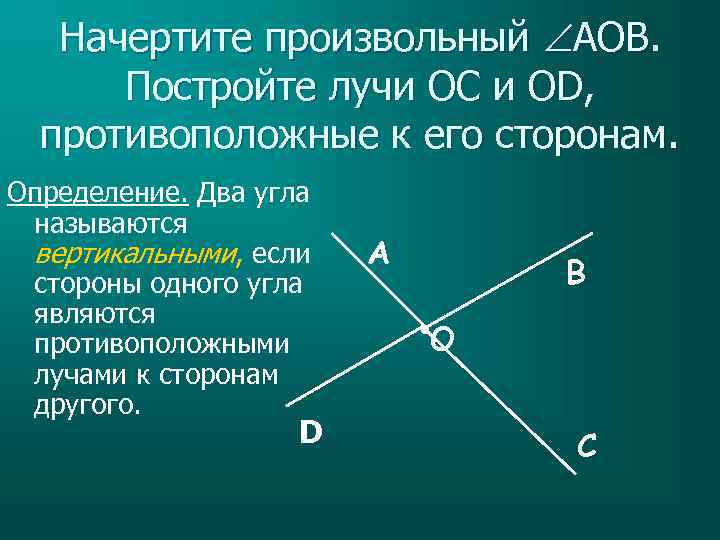Начертите произвольный AOB. Постройте лучи OC и OD, противоположные к его сторонам. D А В О Определение. Два угла называются вертикальными, если стороны одного угла являются противоположными лучами к сторонам другого. С

Построение вертикальных углов

В 1. Построить угол. 2. Продлить каждую сторону угла за его вершину. 1 2 IIIII I I 0 IIIII I C III IIII 4 D 3 IIIII 5 IIII II IIIII 6 IIII I IIIIII 7 IIIII О 9 IIII 8 10 IIIII 12 IIIII 11 IIIII I IIIII 17 16 IIIIII 15 IIIII 14 IIIII I IIIII 13 IIIII 0 IIIIIII 1 2 IIII II IIII 3 IIIII 4 IIIIII 5 I IIIII 6 IIIII 7 IIII 8 IIII II 9 IIIII 10 IIIII 11 IIII 12 IIII II IIII 13 IIIII 1 I IIII 4 IIIII 15 IIIIII 16 IIIII 17 IIII А

Свойство вертикальных углов Теорема. Вертикальные A D O B C углы равны. Дано: AOD и COB – вертикальные. Доказать: AOD= COB Доказательство. Каждый из углов AOD и COB является смежным с углом AOB. По свойству смежных углов: AOD + AOB = 180 и COВ + AOB = 180. Имеем: AOD = 180 – AOB и COB = 180 – AOB, значит, AOD = COB

Решите задачу по чертежу Решение:

Закончи предложение n n n Если один из смежных углов равен 50°, то другой равен… 130° Угол, смежный с прямым, … прямой Если один из вертикальных углов прямой, то второй. . . прямой Угол смежный с острым… тупой Если один из вертикальных углов равен 25°, то второй угол равен… 25°

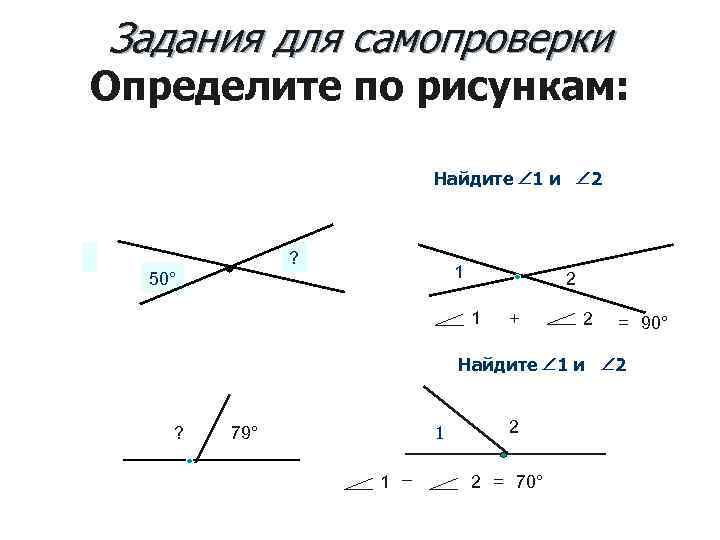Задания для самопроверки Определите по рисункам: Найдите 1 и 2 ? 1 50° 2 1 + 2 = 90° Найдите 1 и 2 ? 11 79° 1 _ 2 2 = 70°

Образец оформления решения задачи При пересечении двух прямых образовалось четыре угла. Один из них равен 430. Найдите величины остальных углов. F M Дано: МК PF = О МОF = 43° 43 0 Найти: FOK, KOP, POM. Решение: O P МОF и KOP вертикальные, значит, по свойству вертикальных углов, МОF = KOP , KOP = 43° МОF + FOK = 180°, так как они смежные. Отсюда FOK = 180°- 43°=137° K FOK и POM вертикальные, значит FOK = POM , POM =137° Ответ: 1370, 430, 1370