4- пр сложной функ.pptx
- Количество слайдов: 13

ТЕМА: Урок 44 -45
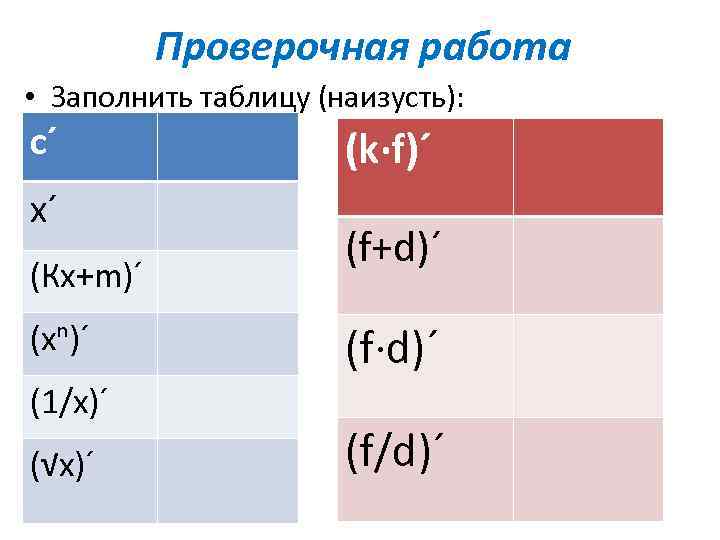
Проверочная работа • Заполнить таблицу (наизусть): с´ х´ (Кх+m)´ (хⁿ)´ (1/х)´ (√х)´ (k·f)´ (f+d)´ (f·d)´ (f/d)´

Изложение нового материала Дано: Решение. • f(x)=х • f(2)=2 = • g(x)=√х • h(x)=3 х+5 • g(16) =√ 16= • p(x)=х +1 • h(0)=3· 0+5= Найти: • p(-1)=(-1) +1= • • f(2) g(16) h(0) p(-1)

Общий вид сложной функции: h(x)= g(f(x)) • Определение. Если функция у=f(х) имеет производную в точке х0, а функция g(у) имеет производную в точке у0=f(х0), то сложная функция h(x)= g(f(x)) также имеет производную в точке х0, причем h´(x 0)= g´(х0)· f´(х0)

Дано: • • Изложение нового материала f(x)=х g(x)=√х h(x)=3 х+5 p(x)=х +1 Найти: • 1. f(h(x))= • 2. f(p(x))= • 3. g(h(x))= • 4. g(р(x))= • 5. h(g(x))= • 6. p(g(x))= Решение.

Вычислить производные сложных функций h´(х)=? № 1. h(x)= Решение:

Вычислить производные сложных функций h´(х)=? № 2. h(x)= (х³-х) 10 Решение:

Вычислить производные сложных функций h´(х)=? № 3. h(x)= (7 х-1)¯³ Решение:

Вычислить производные сложных функций h´(х)=? № 4. h(x)= Решение:

Вычислить производные сложных функций h´(х)=? № 5. h(x)=(2 х+3) Решение:

Вычислить производные сложных функций h´(х)=? • 6. h(x)= Решение:

Вычислить производные сложных функций: h´(х)=? • Самостоятельная работа • • 1) 2) 3) 4) у=(4 х-9) у=(х/3 +2) у= (5 х+1)³ у= • 5) у= • Самостоятельная работа • • 1) 2) 3) 4) у=(1 -9 х) у=(х +х/2) у= (5+2 х)³ у= • 5) у=

Домашнее задание • Стр. 165 • § 33, п. 3 • Найти значение производной функции в точке х0: • Ν 776(а) • Задачник с. 118 • Ν 776(а) • Ν 779(а) у= (3 х-2) х0=3 , Ν 779(а) у= √ 6 х-1, х0=5 Ответ: 3· 7 3√ 29/29 ;
4- пр сложной функ.pptx