Случ.процессы.ppt
- Количество слайдов: 28
 Тема Случайные процессы и поля
Тема Случайные процессы и поля
 Литература n n Никитин А. А. Теоретические основы обработки геофизической информации / А. А. Никитин - М : Изд-во «Недра» , 1986. - 340 с. http: //www. intuit. ru СИГНАЛЫ И ЛИНЕЙНЫЕ СИСТЕМЫ. ТЕМАТИЧЕСКИЕ ЛЕКЦИИ. Григорьев Юрий Игоревич http: //www. grigoyur. ru/grigoyurbio. htm Научная библиотека избранных естественно-научных изданий научная-библиотека. рф http: //www. sernam. r
Литература n n Никитин А. А. Теоретические основы обработки геофизической информации / А. А. Никитин - М : Изд-во «Недра» , 1986. - 340 с. http: //www. intuit. ru СИГНАЛЫ И ЛИНЕЙНЫЕ СИСТЕМЫ. ТЕМАТИЧЕСКИЕ ЛЕКЦИИ. Григорьев Юрий Игоревич http: //www. grigoyur. ru/grigoyurbio. htm Научная библиотека избранных естественно-научных изданий научная-библиотека. рф http: //www. sernam. r
 определение n Случайным процессом (СП) называется непрерывная или дискретная функция, которая в результате эксперимента принимает тот или иной вид, заранее неизвестно, какой именно. n Аргументы СП : время (t) расстояние (x) глубина (h)
определение n Случайным процессом (СП) называется непрерывная или дискретная функция, которая в результате эксперимента принимает тот или иной вид, заранее неизвестно, какой именно. n Аргументы СП : время (t) расстояние (x) глубина (h)
 реализация и сечение случайного процесса n Конкретный вид, который принимает случайный процесс в результате эксперимента, называется реализацией случайного процесса. n Значение реализаций в конкретный момент времени t – сечение случайного процесса
реализация и сечение случайного процесса n Конкретный вид, который принимает случайный процесс в результате эксперимента, называется реализацией случайного процесса. n Значение реализаций в конкретный момент времени t – сечение случайного процесса
 реализация и сечение случайного процесса Случайная величина Случайный процесс описывается семейством реализаций
реализация и сечение случайного процесса Случайная величина Случайный процесс описывается семейством реализаций
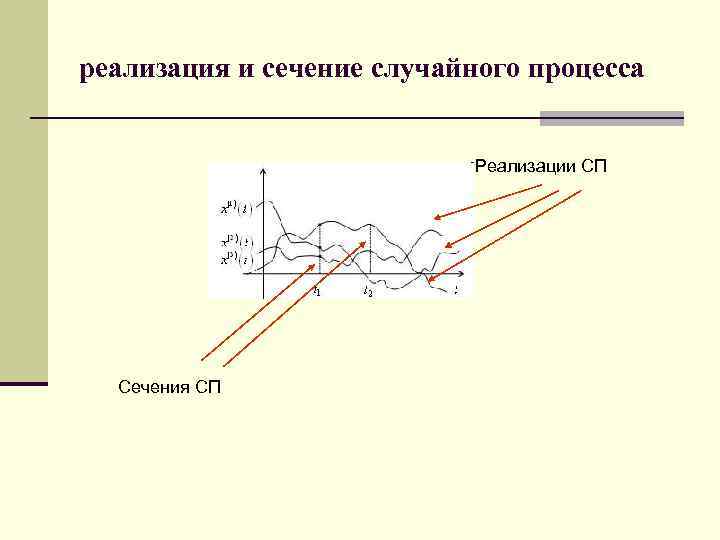 реализация и сечение случайного процесса Реализации СП Сечения СП
реализация и сечение случайного процесса Реализации СП Сечения СП
 замечание Случайный процесс носит двойственный характер: n в каждом конкретном эксперименте он представлен своей реализацией – неслучайной функцией времени. nслучайный процесс описывается совокупностью случайных величин.
замечание Случайный процесс носит двойственный характер: n в каждом конкретном эксперименте он представлен своей реализацией – неслучайной функцией времени. nслучайный процесс описывается совокупностью случайных величин.
 Случайный процесс, рассматриваемый в фиксированный момент времени, является случайной величиной , следовательно можно определить следующие характеристики случайного процесса 1. Математическое ожидание случайного процесса 2. Дисперсия случайного процесса
Случайный процесс, рассматриваемый в фиксированный момент времени, является случайной величиной , следовательно можно определить следующие характеристики случайного процесса 1. Математическое ожидание случайного процесса 2. Дисперсия случайного процесса
 Характеристики случайного процесса 1. Математическое ожидание случайного процесса 2. Дисперсия случайного процесса и среднеквадратическое отклонение
Характеристики случайного процесса 1. Математическое ожидание случайного процесса 2. Дисперсия случайного процесса и среднеквадратическое отклонение
 Характеристики случайного процесса 1. Математическое ожидание случайного процесса 2. Дисперсия случайного процесса 3. ?
Характеристики случайного процесса 1. Математическое ожидание случайного процесса 2. Дисперсия случайного процесса 3. ?
 Автокорреляционная функция СП АКФ Неслучайная функция двух аргументов ti. tj , которая для каждых двух значений ti и tj равна корреляционному моменту соответствующих сечений СП
Автокорреляционная функция СП АКФ Неслучайная функция двух аргументов ti. tj , которая для каждых двух значений ti и tj равна корреляционному моменту соответствующих сечений СП
 Характеристики корреляционной связи
Характеристики корреляционной связи
 Автокорреляционная функция СП АКФ Автокорреляционная функция Нормированная автокорреляционная функция
Автокорреляционная функция СП АКФ Автокорреляционная функция Нормированная автокорреляционная функция
 Свойства АКФ 1. Симметричность: 2. Дисперсия СП выражается через АКФ: 3. Суммирование неслучайной функции и случайного процесса не изменяет АКФ 4. При умножение неслучайной функции и случайного процесса АКФ имеет вид:
Свойства АКФ 1. Симметричность: 2. Дисперсия СП выражается через АКФ: 3. Суммирование неслучайной функции и случайного процесса не изменяет АКФ 4. При умножение неслучайной функции и случайного процесса АКФ имеет вид:
 RX(ti, tj) = M{X(t 1) X(t 2)}.
RX(ti, tj) = M{X(t 1) X(t 2)}.
 АКФ коррелированных и некоррелированных СП n пространство состояний двух процессов практически одно и то же, динамика развития процессов в реализациях существенно различается. n Единичные реализации коррелированных процессов в произвольный момент времени могут быть такими же случайными, как и некоррелированных, n Динамика развития единичной реализации коррелированного процесса по сравнению с некоррелированным является более плавной. В коррелированном процессе имеется определенная связь между последовательными значениями случайных величин. n Оценка степени статистической зависимости мгновенных значений какого-либо процесса Х(t) в произвольные моменты времени t 1 и t 2 и производится функцией автокорреляции (АКФ).
АКФ коррелированных и некоррелированных СП n пространство состояний двух процессов практически одно и то же, динамика развития процессов в реализациях существенно различается. n Единичные реализации коррелированных процессов в произвольный момент времени могут быть такими же случайными, как и некоррелированных, n Динамика развития единичной реализации коррелированного процесса по сравнению с некоррелированным является более плавной. В коррелированном процессе имеется определенная связь между последовательными значениями случайных величин. n Оценка степени статистической зависимости мгновенных значений какого-либо процесса Х(t) в произвольные моменты времени t 1 и t 2 и производится функцией автокорреляции (АКФ).
 Нестационарные процессы n В общем случае значения функций математического ожидания, дисперсии и корреляции могут изменяться во времени. n Такие процессы составляют класс нестационарных процессов.
Нестационарные процессы n В общем случае значения функций математического ожидания, дисперсии и корреляции могут изменяться во времени. n Такие процессы составляют класс нестационарных процессов.
 Процесс нестационарный по ?
Процесс нестационарный по ?
 Процесс нестационарный по ?
Процесс нестационарный по ?
 Стационарные процессы n Процесс называют стационарным, если на интервале его существования выполняются условия постоянства математического ожидания и дисперсии, а корреляционная функция является функцией только разности аргументов
Стационарные процессы n Процесс называют стационарным, если на интервале его существования выполняются условия постоянства математического ожидания и дисперсии, а корреляционная функция является функцией только разности аргументов
 Стационарные процессы Корреляционная функция стационарного процесса не зависит от начала отсчета t, т. е. зависит только от разности моментов времени
Стационарные процессы Корреляционная функция стационарного процесса не зависит от начала отсчета t, т. е. зависит только от разности моментов времени
 Стационарные процессы Корреляционная функция стационарного случайного процесса имеет следующие свойства: 1. 2. 3.
Стационарные процессы Корреляционная функция стационарного случайного процесса имеет следующие свойства: 1. 2. 3.
 Стационарные случайные процессы n Стационарные случайные процессы наиболее часто встречаются при решении физических и технических задач. n случайная функция считается стационарной, если ее математическое ожидание постоянно, а корреляционная функция зависит только от одного аргумента. n Случайные процессы, удовлетворяющие условиям стационарности на ограниченных, интересующих нас интервалах, также обычно относят к числу стационарных в широком смысле и называют квазистационарными.
Стационарные случайные процессы n Стационарные случайные процессы наиболее часто встречаются при решении физических и технических задач. n случайная функция считается стационарной, если ее математическое ожидание постоянно, а корреляционная функция зависит только от одного аргумента. n Случайные процессы, удовлетворяющие условиям стационарности на ограниченных, интересующих нас интервалах, также обычно относят к числу стационарных в широком смысле и называют квазистационарными.
 Эргодические процессы n Большинство стационарных случайных процессов обладает эргодическим свойством. n Сущность его заключается в том, что по одной достаточно длинной реализации процесса можно судить о всех его статистических свойствах так же, как по любому количеству реализаций.
Эргодические процессы n Большинство стационарных случайных процессов обладает эргодическим свойством. n Сущность его заключается в том, что по одной достаточно длинной реализации процесса можно судить о всех его статистических свойствах так же, как по любому количеству реализаций.
 замечание n Свойством эргодичности обладают многие случайные процессы n Все стационарные обладают свойством эргодичности
замечание n Свойством эргодичности обладают многие случайные процессы n Все стационарные обладают свойством эргодичности
 Автокорреляционная функция СП АКФ AKФ прямоугольного импульса
Автокорреляционная функция СП АКФ AKФ прямоугольного импульса
 Автокорреляционная функция и ее применение в геофизике n n n n Корреляционные характеристики В данном блоке объединены модули, позволяющие оценить корреляционные характеристики геополей: одномерные и двумерные автокорреляционные функции АКФ(m) и ДАКФ(m, p), одномерные и двумерные взаимно-корреляционные функции ВКФ(m) и ДАКФ(m, p), трехмерные автокорреляционные функции ТАКФ(m, p, s) и т. д. 2. 1. Автокорреляционная функция Программа предназначена для расчета автокорреляционной функции для каждого профиля исходной сети. 2. 2. Взаимно-корреляционная функция между профилями Эта программа предназначена для вычисления взаимно-корреляционной функции ВКФ(m) между соседними профилями слоев исходной сети. 2. 3. Взаимно-корреляционная функция между полями Эта программа предназначена для вычисления взаимно-корреляционной функции между двумя различными признаками двух сетей B(m). 2. 4. Двумерная автокорреляционная функция Модуль предназначен для оценки корреляционных свойств поля по площади путем расчета двумерной автокорреляционной функции. 2. 5. Двумерная взаимно-корреляционная функция Этот модуль предназначен для расчета двумерной взаимно-корреляционной функции между двумя f 1 и f 2 признаками сети. С помощью двумерной взаимно-корреляционной функции оцениваются корреляционные связи между двумя признаками по площади. Двумерная взаимно-корреляционная функция предназначена для анализа корреляционных связей между двумя признаками по площади и построения двумерных фильтров. 2. 6. Трехмерная автокорреляционная функция Эта программа предназначена для расчета трехмерной автокорреляционной функции ТАКФ(m, p, k) для признака сети. Трехмерная автокорреляционная функция позволяет детально изучить корреляционные характеристики поля в пространстве. На основе ТАКФ(m, p, k) осуществляется расчет весовых коэффициентов трехмерных фильтров. 2. 7. Расчет коэффициента корреляции в скользящем окне Программа предназначена для расчета обычного коэффициента корреляции и коэффициента ранговой корреляции Спирмена между двумя признаками в скользящем трехмерном окне фиксированных размеров. Высота окна, то есть число профилей (или слоев), может быть равно единице (при работе с двумерными сетями).
Автокорреляционная функция и ее применение в геофизике n n n n Корреляционные характеристики В данном блоке объединены модули, позволяющие оценить корреляционные характеристики геополей: одномерные и двумерные автокорреляционные функции АКФ(m) и ДАКФ(m, p), одномерные и двумерные взаимно-корреляционные функции ВКФ(m) и ДАКФ(m, p), трехмерные автокорреляционные функции ТАКФ(m, p, s) и т. д. 2. 1. Автокорреляционная функция Программа предназначена для расчета автокорреляционной функции для каждого профиля исходной сети. 2. 2. Взаимно-корреляционная функция между профилями Эта программа предназначена для вычисления взаимно-корреляционной функции ВКФ(m) между соседними профилями слоев исходной сети. 2. 3. Взаимно-корреляционная функция между полями Эта программа предназначена для вычисления взаимно-корреляционной функции между двумя различными признаками двух сетей B(m). 2. 4. Двумерная автокорреляционная функция Модуль предназначен для оценки корреляционных свойств поля по площади путем расчета двумерной автокорреляционной функции. 2. 5. Двумерная взаимно-корреляционная функция Этот модуль предназначен для расчета двумерной взаимно-корреляционной функции между двумя f 1 и f 2 признаками сети. С помощью двумерной взаимно-корреляционной функции оцениваются корреляционные связи между двумя признаками по площади. Двумерная взаимно-корреляционная функция предназначена для анализа корреляционных связей между двумя признаками по площади и построения двумерных фильтров. 2. 6. Трехмерная автокорреляционная функция Эта программа предназначена для расчета трехмерной автокорреляционной функции ТАКФ(m, p, k) для признака сети. Трехмерная автокорреляционная функция позволяет детально изучить корреляционные характеристики поля в пространстве. На основе ТАКФ(m, p, k) осуществляется расчет весовых коэффициентов трехмерных фильтров. 2. 7. Расчет коэффициента корреляции в скользящем окне Программа предназначена для расчета обычного коэффициента корреляции и коэффициента ранговой корреляции Спирмена между двумя признаками в скользящем трехмерном окне фиксированных размеров. Высота окна, то есть число профилей (или слоев), может быть равно единице (при работе с двумерными сетями).



