Тема. «Системы линейных алгебраических


Тема. «Системы линейных алгебраических уравнений» Основные понятия: 1. Общий вид, классификация, матричный вид 2. Методы решения СЛАУ 3. Теорема Кронекера-Капелли 4. Модель Леонтьева. Межотраслевой баланс завершить

1. Общий вид, классификация, матричный вид Система m линейных уравнений с n неизвестными имеет вид: где коэффициенты при неизвестных, свободные коэффициенты. далее назад
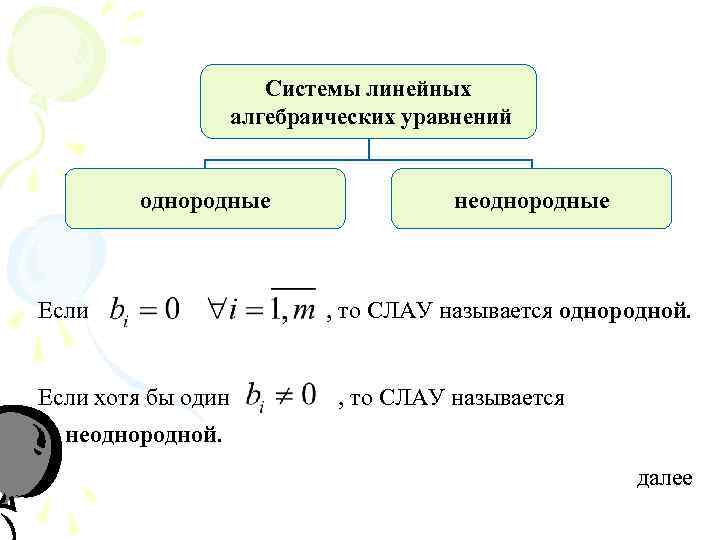
Системы линейных алгебраических уравнений однородные неоднородные Если , то СЛАУ называется однородной. Если хотя бы один , то СЛАУ называется неоднородной. далее
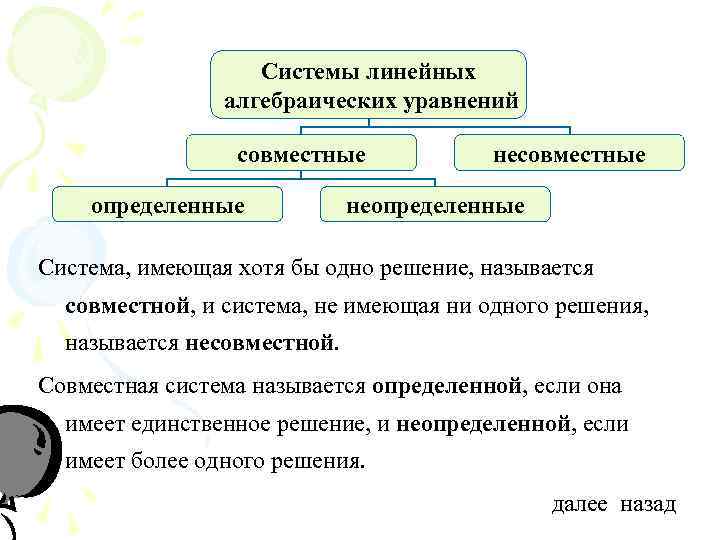
Системы линейных алгебраических уравнений совместные несовместные определенные неопределенные Система, имеющая хотя бы одно решение, называется совместной, и система, не имеющая ни одного решения, называется несовместной. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если имеет более одного решения. далее назад

Выражение «решить СЛАУ» означает выяснить, совместна СЛУ или несовместна, в случае совместности – найти все ее решения. Решением СЛАУ называется упорядоченная совокупность чисел , подстановка которых в СЛАУ обращает каждое ее уравнение в тождество. Пример 1. далее назад

Пример 1. Установить совместность систем уравнений и решить их, если они совместны Решение 1. 1) Решение 1. 2) Решение 1. 3) назад

Решение 1. 1): Ответ 1. 1): СЛАУ совместная, определенная, назад

Решение 1. 2): Ответ 1. 2): СЛАУ совместная, неопределенная, назад

Решение 1. 3): Ответ 1. 3): СЛАУ несовместна. назад

Представить СЛАУ в матричном виде : - основная матрица системы (матрица основных коэффициентов), - вектор правых частей (матрица-столбец свободных коэффициентов), - матрица-столбец неизвестных. На основании согласованности матрицы А с матрицей Х: - матричный вид исходной СЛАУ. назад

2. Методы решения СЛУ 1) Метод Крамера (с помощью определителей) 2) Метод обратной матрицы 3) Метод последовательного исключения неизвестных (Метод Гаусса) Карл Фридрих Гаусс (1777 -1855) - немецкий математик Габриэль Крамер (1704 -1752) – швейцарский математик назад

1) Метод Крамера Метод основан на вычислении определителей, поэтому применим к СЛАУ размерности nxn. Рассмотрим СЛАУ: далее

Введем следующие обозначения: Теорема. Если , то СЛАУ имеет единственное решение , где . (Формулы Крамера) Пример 2. назад

Пример 2. Решить системы уравнений Решение 2. 1) Решение 2. 2) назад

Решение 2. 1): Ответ 2. 1): СЛАУ совместная, определенная, назад
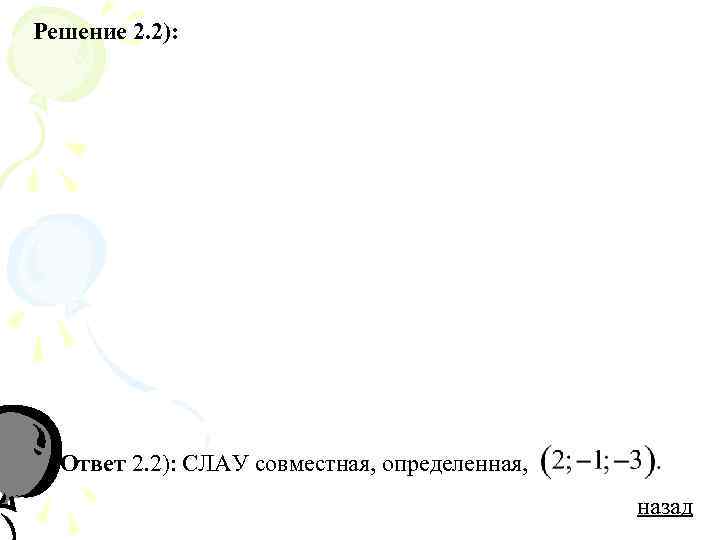
Решение 2. 2): Ответ 2. 2): СЛАУ совместная, определенная, назад

2) Метод обратной матрицы Метод основан на нахождении обратной матрицы, поэтому применим к СЛАУ размерности nxn. Рассмотрим СЛАУ в матричном виде: Пример 3. назад

Пример 3. Решить системы уравнений Решение 3. 1) Решение 3. 2) Решение 3. 3) назад
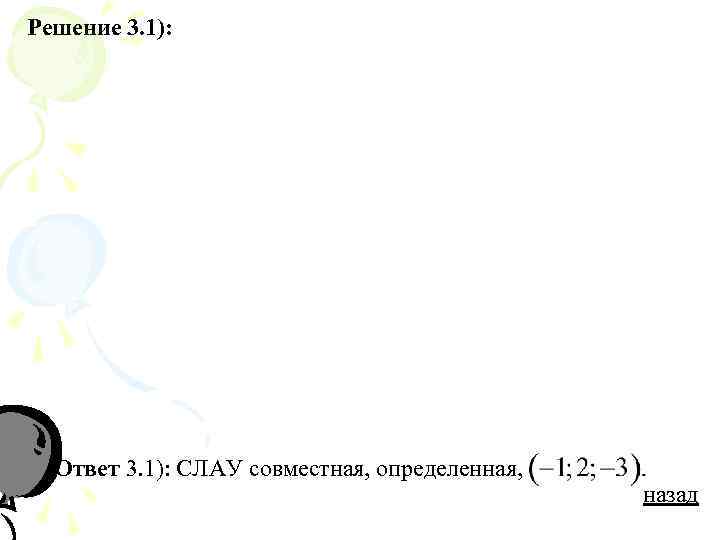
Решение 3. 1): Ответ 3. 1): СЛАУ совместная, определенная, назад

Решение 3. 2): Ответ 3. 2): СЛАУ совместная, определенная. назад
Решение 3. 3): Ответ 3. 3): СЛАУ совместная, определенная. назад

3) Метод последовательного исключения неизвестных (Метод Гаусса) Рассмотрим СЛАУ: Данный метод применим к СЛУ любой размерности. далее назад

Алгоритм метода Гаусса: 1) Метод Гаусса удобно осуществлять в матричном виде. Для этого исходную СЛАУ записывают в виде расширенной матрицы (A|B): 2) С помощью элементарных преобразований сводят матрицу (A|B) к ступенчатому виду или квазитреугольной форме. 3) По полученной матрице ступенчатого вида находят решение СЛАУ методом исключения переменных. Пример 4. назад

Пример 4. Решить системы уравнений Решение 4. 1) Решение 4. 2) Решение 4. 3) назад

Решение 4. 1): Ответ 4. 1): СЛАУ совместная, определенная, назад

Решение 4. 2): Ответ 4. 2): СЛАУ совместная, неопределенная, назад

Решение 4. 3): Ответ 4. 3): СЛАУ несовместна. назад

3. Теорема Кронекера-Капелли Помимо метода Гаусса, на вопрос совместна ли СЛАУ или нет можно воспользоваться теоремой Кронекера-Капелли. Теорема Кронекера-Капелли. Для совместимости СЛАУ необходимо и достаточно, чтобы ранг ее основной матрицы был равен рангу расширенной матрицы. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг матрицы совместной системы меньше числа неизвестных, то множество ее решений является бесконечным. Пример 5. назад

Пример 5. Установить совместность систем уравнений и решить их, если они совместны Решение 5. 1) Решение 5. 2) Решение 5. 3) назад

Решение 5. 1): Ответ 5. 1): СЛАУ совместная, определенная, назад

Решение 5. 2): Ответ 5. 2): СЛАУ совместная, неопределенная, назад

Решение 5. 3): Ответ 5. 3): СЛАУ несовместна. назад

Спасибо за внимание! Не забывайте готовиться к лекциям и семинарам! (Тема следующей лекции «Модель Леонтьева» ) Удачи!
Системы линейных алгеб уравненийNew.ppt
- Количество слайдов: 33

