Тема Применение производной И Ньютон Ø Лишь

Тема: «Применение производной»

И. Ньютон Ø «Лишь дифференциальное исчисление дает возможность естествознанию изображать математически не только состояния, но и процессы: движение» .

Цели урока: Ø Общеобразовательные - Закрепить навыки вычисления производных; - Систематизировать и углубить знаний по теме; - Формировать умения комплексного применения знаний, умений, навыков и их перенос в новые условия.

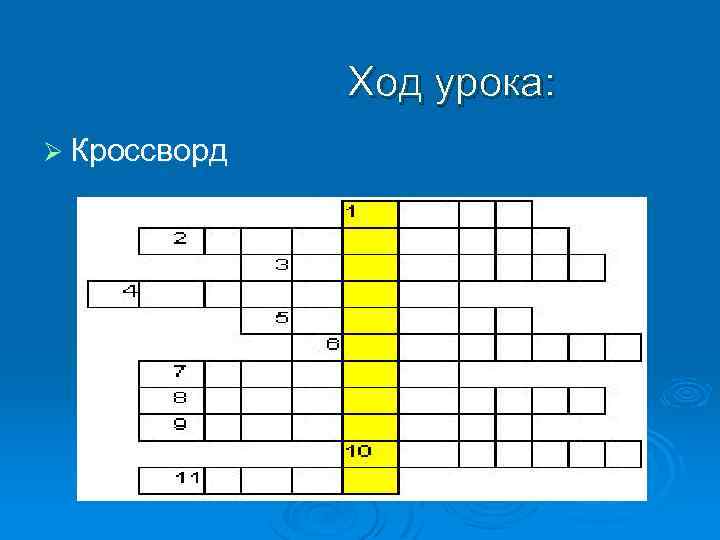Ход урока: Ø Кроссворд

Ø Ø Ø Ø Ø Вопросы к кроссворду: 1. Расстояние между двумя точками, измеренное вдоль траектории движущегося тела. 2. Физическая величина, характеризирующая быстроту изменения скорости 3. Одна из основных характеристик движения. 4. Немецкий философ, математик, физик, один из создателей математического анализа. 5. Наука, изучающая наиболее общие закономерности явлений природы, состав и строение материи, законы ее движения. 6. Изменение положения тела в пространстве относительно некоторой системы отсчета с течением времени. 7. Выдающийся английский физик, именем которого названы основные законы механики. 8. Какие величины определяют положение тела в выбранной системе отсчета 9. Физическая теория, устанавливающая закономерности взаимных перемещений тел в пространстве, и происходящих при этом взаимодействий

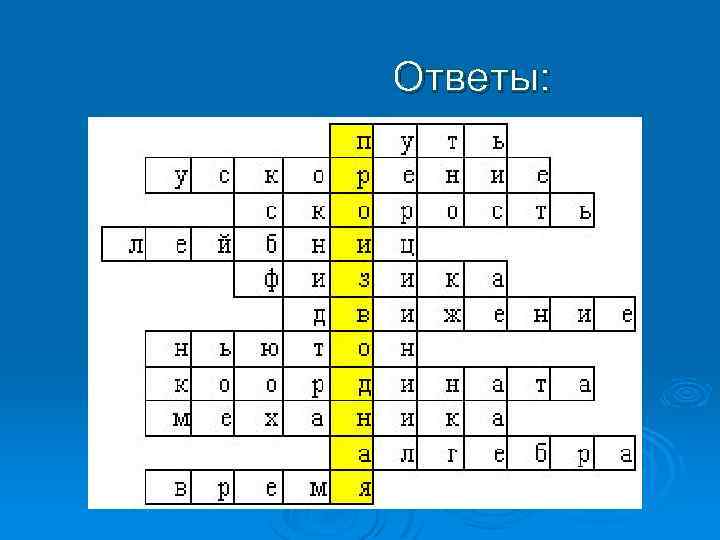Ответы:

Производная - одно из фундаментальных понятий математики. Оно возникло в XVII веке в связи с необходимостью решения ряда задач из физики, механики и математики, но в первую очередь следующих двух: - определение скорости прямолинейного движения ; - построение касательной к кривой.

История возникновения понятия «производная» Ряд задач дифференциального исчисления был решен еще в древности. Они встречались у Евклида. Ø Ряд таких задач был решен Архимедом, разработавшим способ проведения касательной, примененный им к спирали, но применимый для других кривых Ø

Ø Термин «производная» является буквальным переводом на русский французского слова derivee, которое ввёл в 1797 году Жозеф Луи Лагранж (1736 -1813). Он же ввёл современное обозначение у/, f/(х).

Понятие производной встречалось в работах итальянского математика Тартальи (около 1500 - 1557 гг. ) здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.

Ø В 17 веке на основе учения Г. Галилея о движении активно развивалась кинематическая концепция производной.

Ø Различные изложения стали встречаться в работах у Р. Декарта, французского математика Ж. Роберваля, английского ученого Д. Грегори.

Ø Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Эйлер, Гаусс.

Найти соответствие sin (kx+b) c 1 kx ekx+b 3 2 k*xn 4 5 -sin (kx+b) -ksin(kx+b) 8 ax 10 6 cos (kx+b) 11 log a x kekx+b x: ln a 12 0 13 kxn+1 ekx+b 16 15 17 19 kcos(kx+b) k 22 ax lna 23 c 20 k nxn-1 24 25

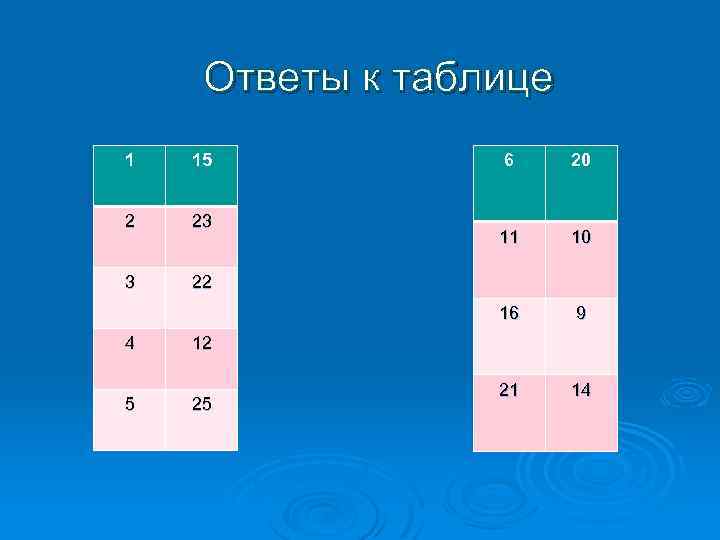Ответы к таблице 1 15 2 23 3 22 5 20 11 10 16 4 6 9 21 14 12 25

И. Ньютон Ø Не найти другого учёного, исследования которого оказали бы столь сильное влияние на историю мировой науки и культуры, как Исаак Ньютон. О нём писали: «Каждый естествоиспытатель безусловно согласится, что механика Ньютона есть основа современной физики. Каждый астроном знает, что современная астрономия начинается с Кеплера и Ньютона. И каждый математик знает, что самым значительным, наиболее важным для физики отделом современной математики является анализ, в основе которого лежат дифференциальное и интегральное исчисления Ньютона» .

Ø Независимо друг от друга И. Ньютон и Г. Лейбниц разработали аппарат дифференциального исчисления, которым мы и пользуемся в настоящее время. И. Ньютон в основном опирался на физические представления о мгновенной скорости движения, считая его очевидным и сводя к нему другие случаи производной.

Ø Для нахождения мгновенной скорости, скорости в данный момент, необходимо найти отношение приращения пути (по современной терминологии) к приращению времени, а затем — предел этого отношения, т. е. взять «последнее отношение» , когда приращение времени стремится к нулю. Так Ньютон ввел отыскание «последних отношений» , производных, которые он называл флюксиями. . .

Свои открытия Ньютон сделал раньше Лейбница, но своевременно не опубликовал их; все его математические сочинения были изданы после того, как он стал знаменитым. Ø «Метод флюксий» увидел свет только после смерти автора в 1736 году. Ø

Найти производную функции

Найти производную функции

Ответы к самостоятельной работе

Г. Лейбниц Ø ЛЕЙБНИЦ Готфрид Вильгельм(16461716), немецкий философ, математик, физик, языковед. В 1676 году Лейбниц выработал первые основания великого математического метода, известного под названием «дифференциальное исчисление» .

В отличие от И. Ньютона, Г. Лейбниц использовал понятие бесконечно малой величины. Ø Факты с достаточной убедительностью доказывают, что Лейбниц хотя и не знал о методе флюксий, но был подведен к открытию письмами Ньютона. Ø Открытие Лейбница по общности, удобству обозначения и подробной разработке метода стало орудием анализа значительно могущественнее и популярнее метода флюксий Ньютона. Ø

Ø Все свободное время он посвятил обработке изобретенного им дифференциального исчисления и в промежуток времени между 1677 и 1684 годами успел создать целую новую отрасль математики.

Ø Долгое время Ньютон и не подозревал, что на континенте успешно занимается подобной проблемой немец Лейбниц. До поры до времени высоко ценившие заслуги друга, в конце концов, ученые втянулись в полемику о приоритете открытия исчисления бесконечно малых.

Ø В письме, написанном в июне 1677 года, Лейбниц прямо раскрывал Ньютону свой метод дифференциального исчисления. Тот на письмо Лейбница не ответил. Ньютон считал, что открытие принадлежит ему навечно. Ученый искренне считал: своевременная публикация не приносит никаких прав. Перед Богом первооткрывателем всегда останется тот, кто открыл первым.

Физический смысл производной Ø Производная в физике есть быстрота или скорость изменения какой-либо величины с течением времени. υ (t) = х/(t) – скорость a (t) = υ/ (t) – ускорение J (t) = q/(t) - сила тока C(t) = Q/(t) - теплоемкость ω (t)= φ/(t) - угловая скорость N(t) = A/(t) - мощность

Задача по химии: Пусть количество вещества, вступившего в химическую реакцию задается зависимостью: р(t) = t 2/2 + 3 t – 3 (моль) Найти скорость химической реакции через 3 секунды.

Решение: Понятие на языке химии Понятие на языке математики Обозначение Количество в-ва в момент времени p = p (t 0) t 0 Функция Интервал времени ∆t = t– t 0 Приращение аргумента Изменение количества в-ва ∆p= p (t 0+ ∆ t ) – p (t 0) Приращение функции Средняя скорость химической ∆p/∆t реакции Отношение приращёния функции к приращёнию аргумента V (t) = p ‘(t)

Применение производной в биологии Задача: По известной зависимости численности популяции x (t) определить относительный прирост в момент времени t.

Понятие на языке биологии Обозначение Понятие на языке математики Численность в момент времени t 1 x = x (t) Функция Интервал времени Приращение аргумента Изменение численности популяции Скорость изменения численности популяции ∆t = t 2 – t 1 Приращение функции ∆x = x (t 2) – x (t 1) Отношение приращения функции к приращению аргумента ∆x /∆t Производная Р = х‘ (t)

Применение производной в географии

Задача : Ø Вывести формулу для вычисления численности населения на ограниченной территории в момент времени t. ЭТО Я ЭТО Я

Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.

Решение: Пусть у=у(t)- численность населения. Рассмотрим прирост населения за t=t-t 0 y=k y t, где к = к р – кс –коэффициент прироста (к р – коэффициент рождаемости, кс – коэффициент смертности) y/ t=k y При t 0 получим lim y/ t=у’ у’=к у

Применение производной экономике • Производительность труда есть производная от объема произведенной продукции по времени. П=V‘ (t) • Аналогичным образом могут быть определены предельная выручка, предельный доход, предельный продукт, предельная полезность, предельная производительность и другие предельные величины. в Таким образом, производная выступает как скорость изменения некоторого экономического объекта (процесса) по времени.

Применение производной в нашей жизни Ø Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции; Ø Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей; Ø Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.

Задача Ø Тело массой 10 кг движется по закону s=t 3/3 -6 t (s в метрах , t в секундах). Найдите силу , действующую на тело, и его кинетическую энергию через 3 с от начала движения.

Решение 1) найдём кинетическую энергию данного тела для любого момента времени : Ø Е к =(mv 2)/2 , но v=s'=(t 3/3 -6 t)'=t 2 -6. Ø Таким образом, Eк=(m*(t 2 -6)2)/2 Ø (E k) t=3 =(10*(32 -6)2)/2=(10*9)/2=45(Дж) Ø Ø 2) силу , действующую на тело в момент времени t, найдём по формуле: F=ma, где а =s"=(s‘)‘=V'; a=v'=(t 2 -6)'=2 t. Ø Таким образом, F=m*2 t ; и значение F для момента времени 3 с : F =10*2*3=60 (H). t=3

Задача Ø Тело движется вертикально вверх по закону: s=40 t – (qt 2)/2 (s в метрах, q – ускорение свободного падения , принять равным 10 м/с2). Найти максимальную высоту подъёма данного тела.

Решение Очевидно , чтобы узнать максимальную высоту подъёма тела, надо знать время его подъёма. Время подъёма найдем из следующих соображений : в момент подъёма тела на максимальную высоту его скорость обращается в 0. А так как Ø v=s'=(40 t-(qt 2)/2)'=40 -qt, то имеем: Ø 40 -qt=0 , следовательно qt=40 => t=40/q=4 (c). Ø Таким образом , Ø h =( s ) =40*4 -10*8=160 -80=80 (м) Ø max t=4

Задача Ø Температура тела изменяется по закону T=0. 2 t 2 (t в секундах, T в градусах). Ø С какой скоростью нагревается тело через 10 с после начала нагревания?

Решение При нагревании тела его температура изменяется в зависимости от времени нагрева , т. е. T=f (t) – температура является функцией от времени. Скорость нагревания тела есть производная температуры по времени , Ø т. е vнагрев T'= d T / d t =(0. 2 t 2)'=0. 4 t Ø (d T/d t ) =0, 4*10= 4 (град/с) Ø Ответ: в момент времени t=10 c тело нагревается со скоростью 4 градуса в секунду Ø t=10

Задача Ø В электрической цепи с активным сопротивлением R=5 Oм протекает заряд Q, изменяющийся от времени по закону : Q=t 3/3 (t в секундах , заряд в Кл). Найти мощность, поглощаемую (выделяемую) нагрузкой (источником тока) , через 2 с от начала включения источника тока.

Решение Мощность, поглощаемая нагрузкой, находится по формуле: P=I 2*R, где I – мгновенное значение силы тока, R – сопротивление нагрузки. Ø Сила тока – это быстрота изменения заряда, т. е. I=Q'=d. Q/dt. Найдём силу тока для любого значения времени : Ø I=Q'=(t 3/3)' = t 2. Для t = 2 c: I =22= 4(A) Ø Ответ: мощность, поглощаемая нагрузкой, P=42*50= 800(Вт) Ø t=2

Рефлексия Оценим нашу работу на уроке. Продолжите фразу: Ø“Сегодня на уроке я узнал…” Ø“Сегодня на уроке я научился…” Ø“Сегодня на уроке я познакомился…” Ø“Сегодня на уроке я повторил…” Ø

Заключение “Музыка может возвышать или умиротворять душу, Живопись – радовать глаз, Поэзия – пробуждать чувства, Философия – удовлетворять потребности разума, Инженерное дело – совершенствовать материальную сторону жизни людей, А математика и физика способны достичь всех этих целей”. Клайн. Американский математик Морис

Спасибо за работу!