Тема Позиционные задачи Цель ознакомиться и научиться решать

Тема: Позиционные задачи Цель: ознакомиться и научиться решать позиционные задачи различными способами. Задачи: 1. 2. 3. Классификация и характеристика позиционных задач Решение задач методом секущих плоскостей Решение задач методом концентрических сфер

Позиционные задачи – задачи, связанные с определением общих элементов различных геометрических образов. Относятся: 1. На порядок расположения геометрических элементов; 2. На взаимное принадлежность геом. образов; 3. Взаимное пересечение геом. образов.

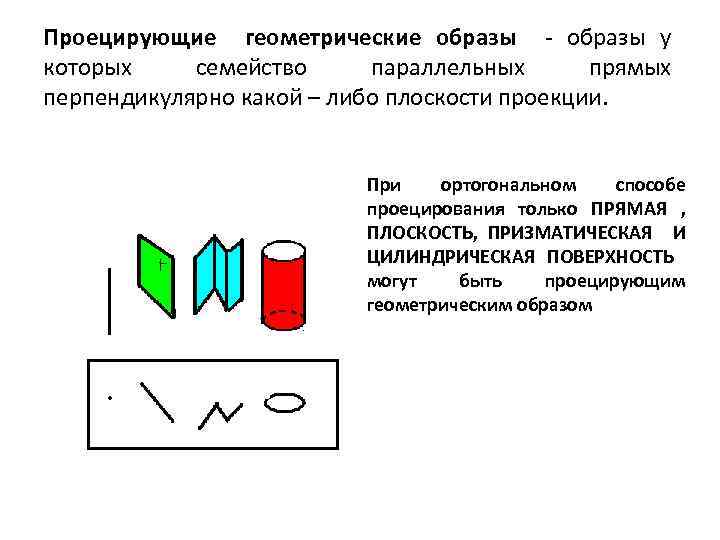Проецирующие геометрические образы - образы у которых семейство параллельных прямых перпендикулярно какой – либо плоскости проекции. При ортогональном способе проецирования только ПРЯМАЯ , ПЛОСКОСТЬ, ПРИЗМАТИЧЕСКАЯ И ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ могут быть проецирующим геометрическим образом

1. Задачи на порядок расположения геом. элементов

2. Задачи на взаимную принадлежность

3. Задачи на взаимное пересечение геом. образов a. линии с линиями b. Линия с поверхностью c. Поверхности с поверхностями b и с – главные позиционные задачи

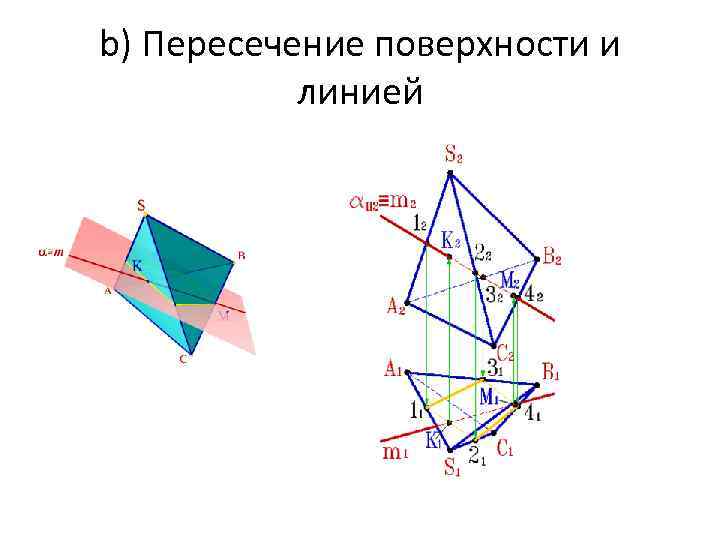b) Пересечение поверхности и линией

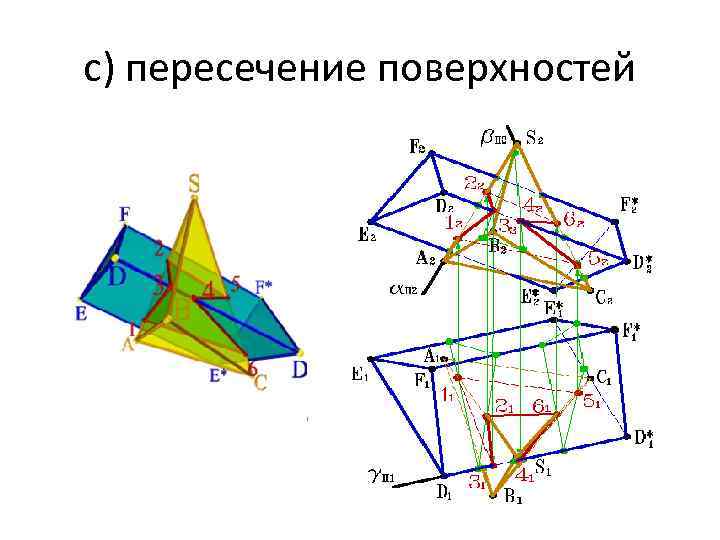с) пересечение поверхностей

Главные позиционные задачи : A. Оба занимают проецирующее положение B. Один занимает проецирующее положение, а другой не проецирующее C. Оба занимают не проецирующее положение

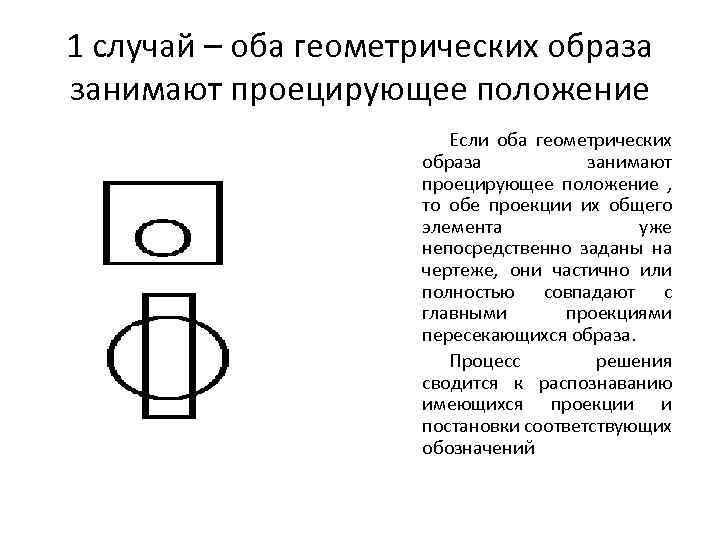1 случай – оба геометрических образа занимают проецирующее положение Если оба геометрических образа занимают проецирующее положение , то обе проекции их общего элемента уже непосредственно заданы на чертеже, они частично или полностью совпадают с главными проекциями пересекающихся образа. Процесс решения сводится к распознаванию имеющихся проекции и постановки соответствующих обозначений

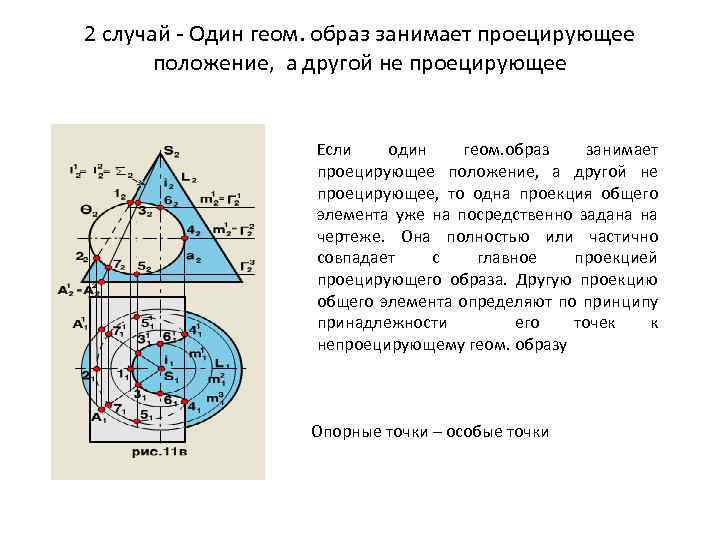2 случай - Один геом. образ занимает проецирующее положение, а другой не проецирующее Если один геом. образ занимает проецирующее положение, а другой не проецирующее, то одна проекция общего элемента уже на посредственно задана на чертеже. Она полностью или частично совпадает с главное проекцией проецирующего образа. Другую проекцию общего элемента определяют по принципу принадлежности его точек к непроецирующему геом. образу Опорные точки – особые точки

3 случай - Оба геометрических образа занимают не проецирующее положение - метод секущих плоскостей; - метод концентрических сфер.

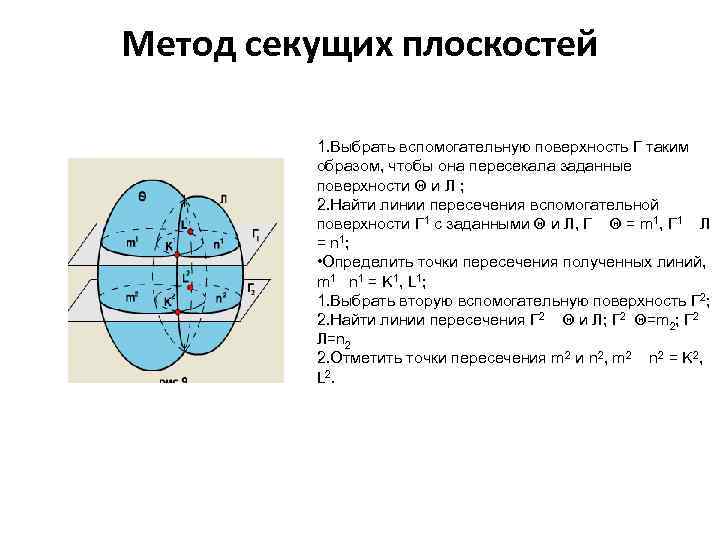Метод секущих плоскостей 1. Выбрать вспомогательную поверхность Г таким образом, чтобы она пересекала заданные поверхности Q и Л ; 2. Найти линии пересечения вспомогательной поверхности Г 1 с заданными Q и Л, Г Q = m 1, Г 1 Л = n 1; • Определить точки пересечения полученных линий, m 1 n 1 = K 1 , L 1 ; 1. Выбрать вторую вспомогательную поверхность Г 2; 2. Найти линии пересечения Г 2 Q и Л; Г 2 Q=m 2; Г 2 Л=n 2 2. Отметить точки пересечения m 2 и n 2, m 2 n 2 = K 2, L 2.

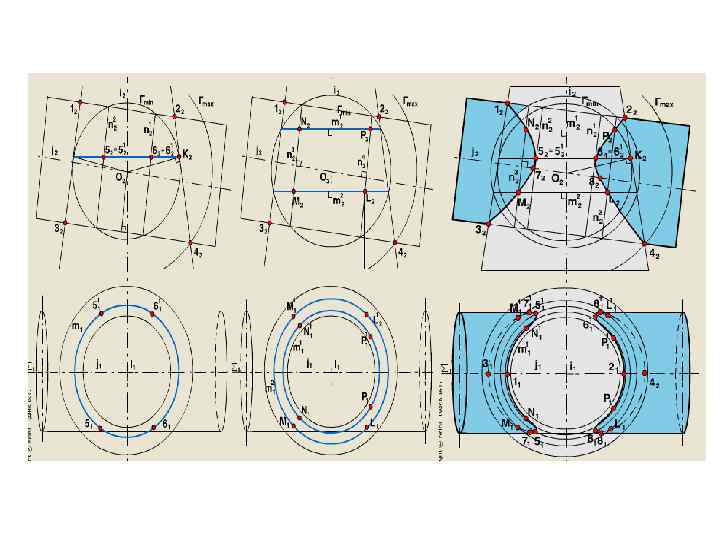
метод концентрических сфер. Алгоритм построений: 1. Найти точку пересечения осей вращения – центр вспомогательных сфер. 2. Обозначить точки пересечения главных меридианов исходных поверхностей. 3. Определить радиус наибольшей вспомогательной сферы Гmax, Его величина равна расстоянию от центра до наиболее удаленнной от него точки пересечения главных меридианов. 4. Найти радиус наименьшей сферы, провести очерк сферы Гmin. Она касается по окружности одной исходной поверхности и пересекает по двум окружностям другую поверхность. Построить проекции этих окружностей (это отрезки прямых) и отметить точки их пересечения. 5. Взять промежуточную сферу. Она пересекает исходные поверхности окружностям. Построить проекции окружностей и отметить их точки пересечения. Проекции окружностей – отрезки прямых.

Домашнее задание • Теорема Монжа