Скачать презентацию ТЕМА Пирамида Её элементы Правильная пирамида Скачать презентацию ТЕМА Пирамида Её элементы Правильная пирамида

98659814.pptx

  • Количество слайдов: 45

ТЕМА ТЕМА

Пирамида. Её элементы. Правильная пирамида. Пирамида. Её элементы. Правильная пирамида.

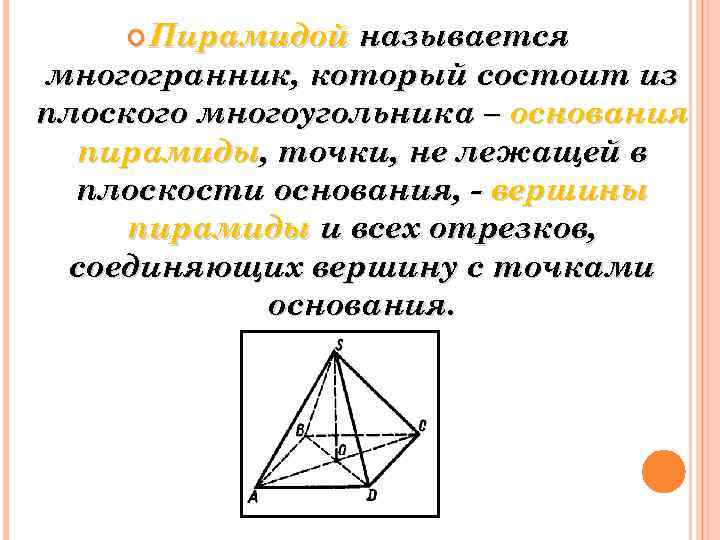Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину с точками основания.

Слово «пирамида» — греческое. По мнению одних исследователей, большая куча пшеницы и стала прообразом Слово «пирамида» — греческое. По мнению одних исследователей, большая куча пшеницы и стала прообразом пирамиды. По мнению других учёных, это слово произошло от названия поминального пирога пирамидальной формы.

Пирамиды майя в Сальвадоре Пирамиды майя в Сальвадоре

Египетские пирамиды — величайшие архитектурные памятники Древнего Египта, среди которых одно из «семи Египетские пирамиды — величайшие архитектурные памятники Древнего Египта, среди которых одно из «семи чудес света» — пирамида Хеопса. Пирамиды представляют собой огромные каменные сооружения пирамидальной формы, использовавшиеся в качестве гробниц для фараонов Древнего Египта. Всего в Египте было обнаружено 118 пирамид.

Пирамиды считаются проводниками космических энергий. Хорошо известно их применение в целительстве и медитации. Пирамиды считаются проводниками космических энергий. Хорошо известно их применение в целительстве и медитации. Фактически, большинство храмов, мечетей, церквей, соборов имеют пирамидо- или куполообразную форму крыши.

СОВРЕМЕННЫЕ ПИРАМИДЫ Самая большая пирамида, высотой 44 метра, расположена в Московской области СОВРЕМЕННЫЕ ПИРАМИДЫ Самая большая пирамида, высотой 44 метра, расположена в Московской области

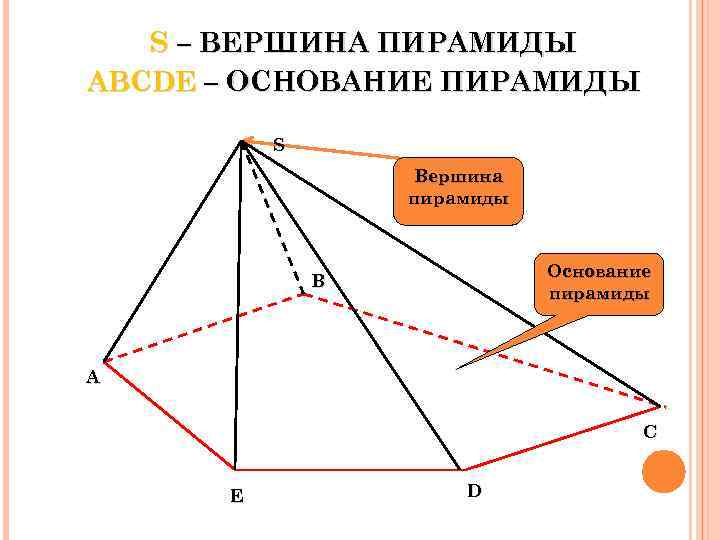S – ВЕРШИНА ПИРАМИДЫ ABCDE – ОСНОВАНИЕ ПИРАМИДЫ S Вершина пирамиды Основание пирамиды B S – ВЕРШИНА ПИРАМИДЫ ABCDE – ОСНОВАНИЕ ПИРАМИДЫ S Вершина пирамиды Основание пирамиды B A C E D

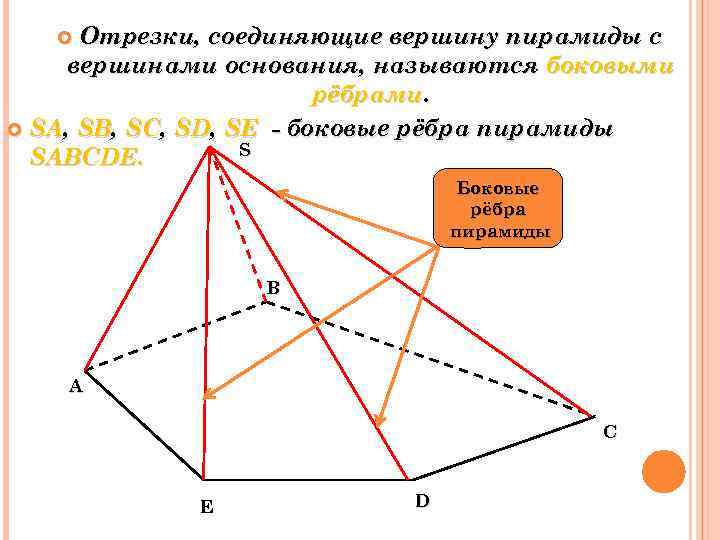Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми рёбрами. SA, SB, SC, SD, Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми рёбрами. SA, SB, SC, SD, SE - боковые рёбра пирамиды S SABCDЕ. Боковые рёбра пирамиды B A C E D

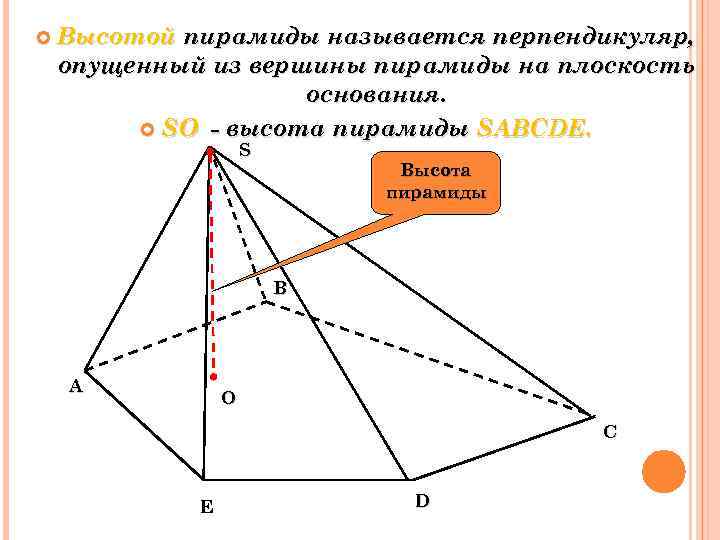Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. SО - Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. SО - высота пирамиды SABCDЕ. S Высота пирамиды B A О C E D

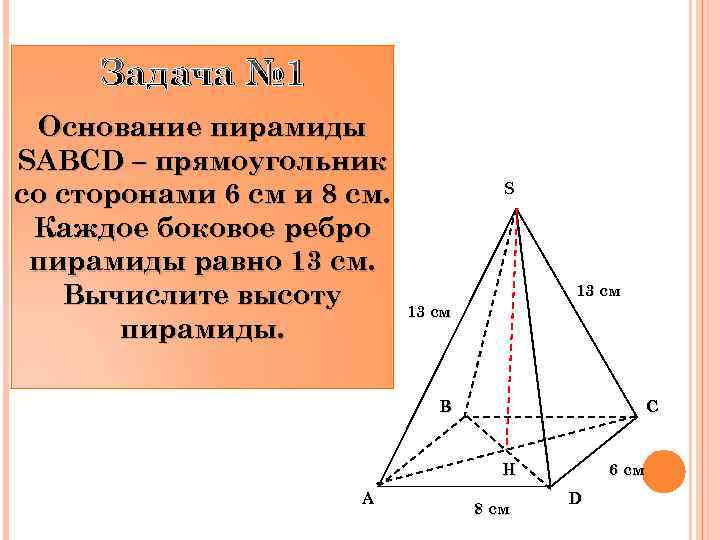Задача № 1 Основание пирамиды SABCD – прямоугольник со сторонами 6 см и 8 Задача № 1 Основание пирамиды SABCD – прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см. Вычислите высоту пирамиды. S 13 см B C Н A 8 см 6 см D

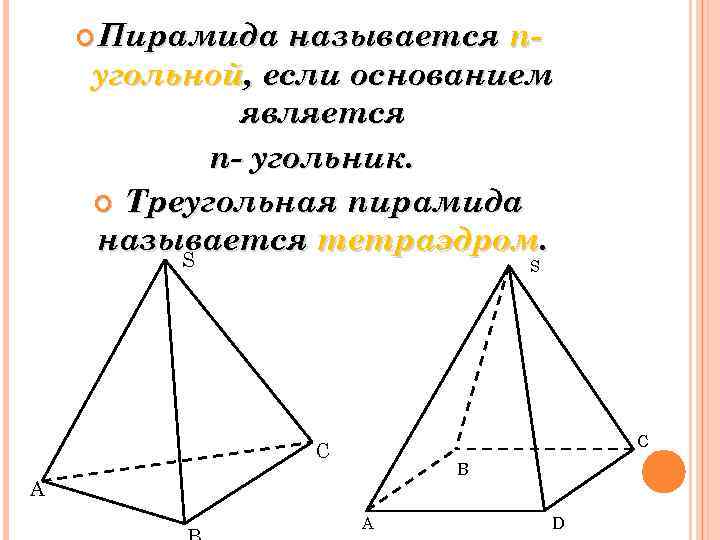Пирамида называется nугольной, если основанием является n- угольник. Треугольная пирамида называется тетраэдром. S Пирамида называется nугольной, если основанием является n- угольник. Треугольная пирамида называется тетраэдром. S S C C B A A D

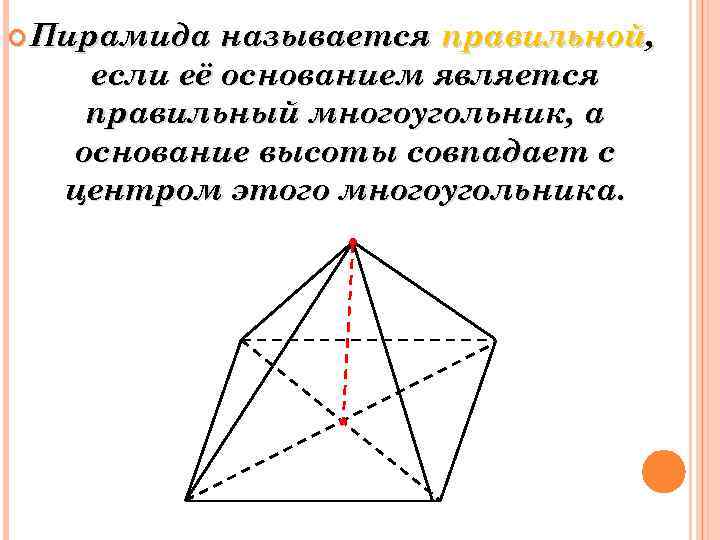Пирамида называется правильной, если её основанием является правильный многоугольник, а основание высоты совпадает Пирамида называется правильной, если её основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника.

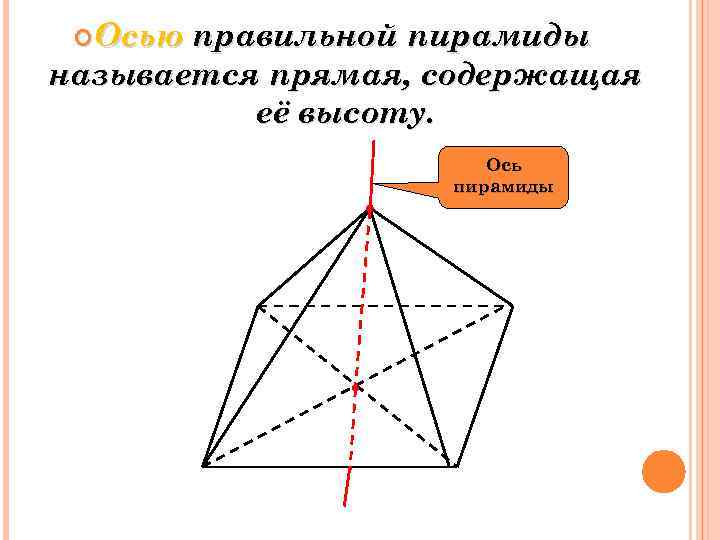Осью правильной пирамиды называется прямая, содержащая её высоту. Ось пирамиды Осью правильной пирамиды называется прямая, содержащая её высоту. Ось пирамиды

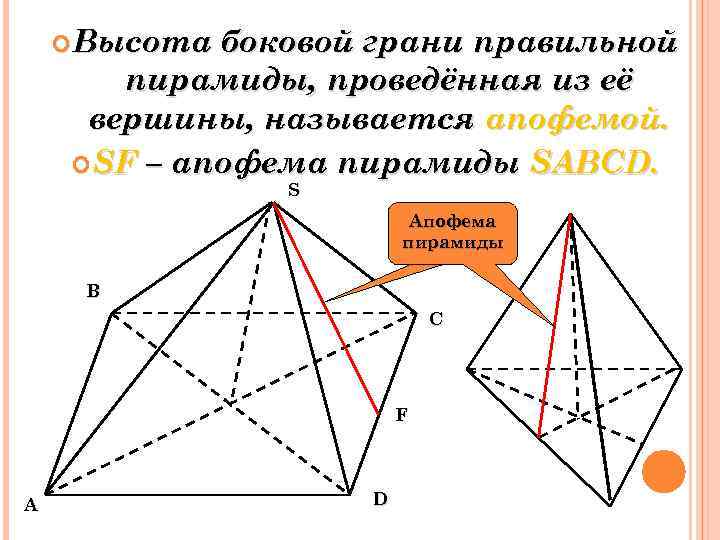Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой. SF – Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой. SF – апофема пирамиды SABCD. S Апофема пирамиды B С F A D

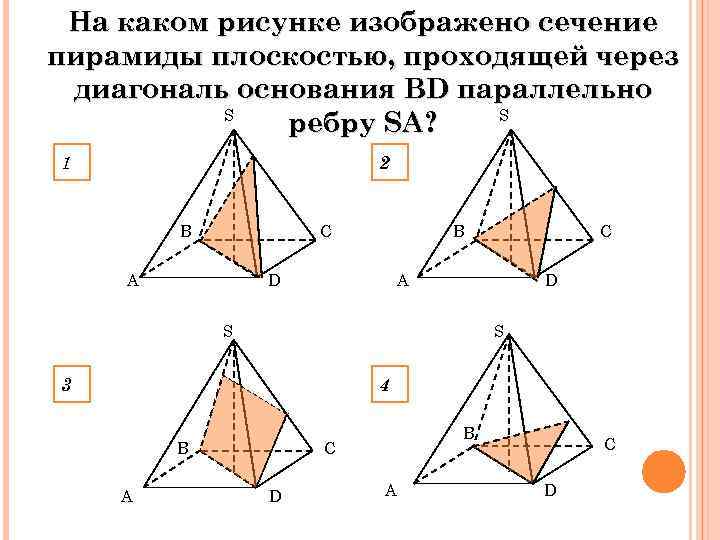На каком рисунке изображено сечение пирамиды плоскостью, проходящей через диагональ основания BD параллельно S На каком рисунке изображено сечение пирамиды плоскостью, проходящей через диагональ основания BD параллельно S S ребру SA? 1 2 C B A B D C A D S S 3 4 B A B C D A C D

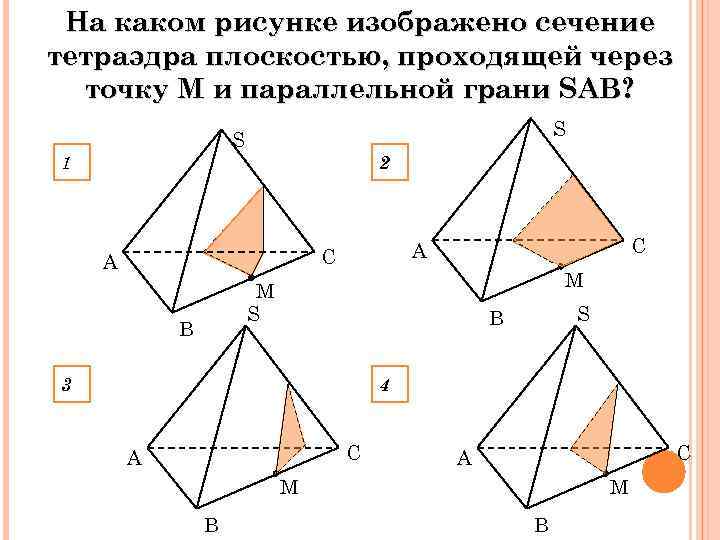На каком рисунке изображено сечение тетраэдра плоскостью, проходящей через точку М и параллельной грани На каком рисунке изображено сечение тетраэдра плоскостью, проходящей через точку М и параллельной грани SAВ? S S 1 2 A C M M S B 3 4 C A M B

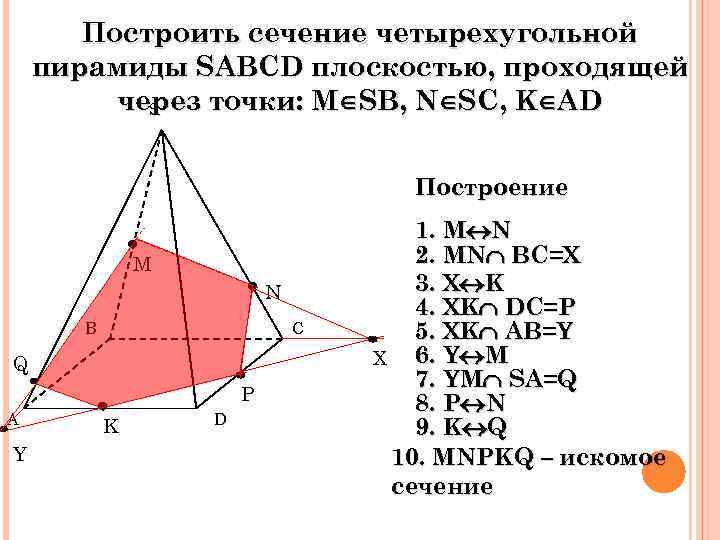Построить сечение четырехугольной пирамиды SABCD плоскостью, проходящей через точки: M SB, N SC, K Построить сечение четырехугольной пирамиды SABCD плоскостью, проходящей через точки: M SB, N SC, K AD S Построение M N B C Q P A Y K D 1. M N 2. MN BC=X 3. X K 4. XK DC=P 5. XK AB=Y X 6. Y M 7. YM SA=Q 8. P N 9. K Q 10. MNPKQ – искомое сечение

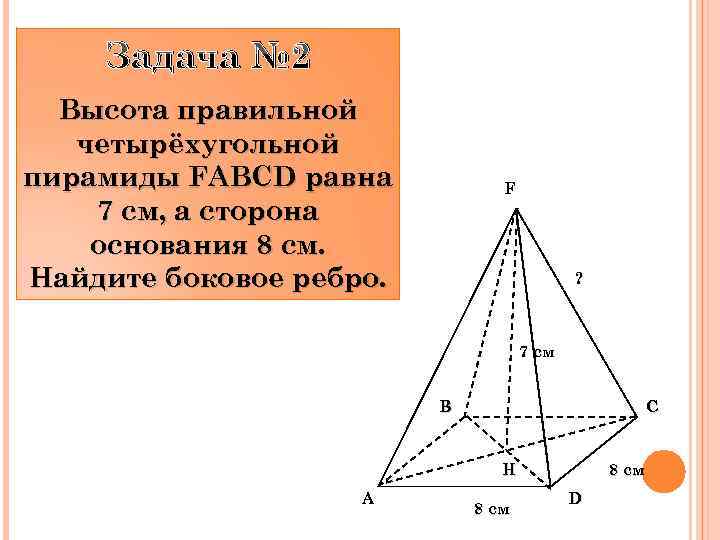Задача № 2 Высота правильной четырёхугольной пирамиды FABCD равна 7 см, а сторона основания Задача № 2 Высота правильной четырёхугольной пирамиды FABCD равна 7 см, а сторона основания 8 см. Найдите боковое ребро. F ? 7 см B C Н A 8 см D

Усечённая пирамида Усечённая пирамида

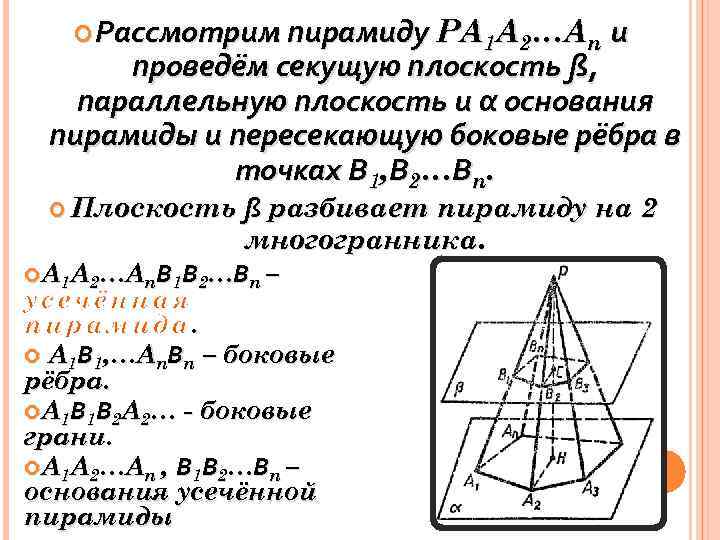Рассмотрим пирамиду PA 1 A 2…An и проведём секущую плоскость ß, параллельную плоскость Рассмотрим пирамиду PA 1 A 2…An и проведём секущую плоскость ß, параллельную плоскость и α основания пирамиды и пересекающую боковые рёбра в точках В 1, В 2…Вn. Плоскость ß разбивает пирамиду на 2 многогранника. A 1 A 2…An. В 1 В 2…Вn – . A 1 В 1, …An. Вn – боковые рёбра. A 1 В 1 В 2 A 2… - боковые грани. A 1 A 2…An , В 1 В 2…Вn – основания усечённой пирамиды

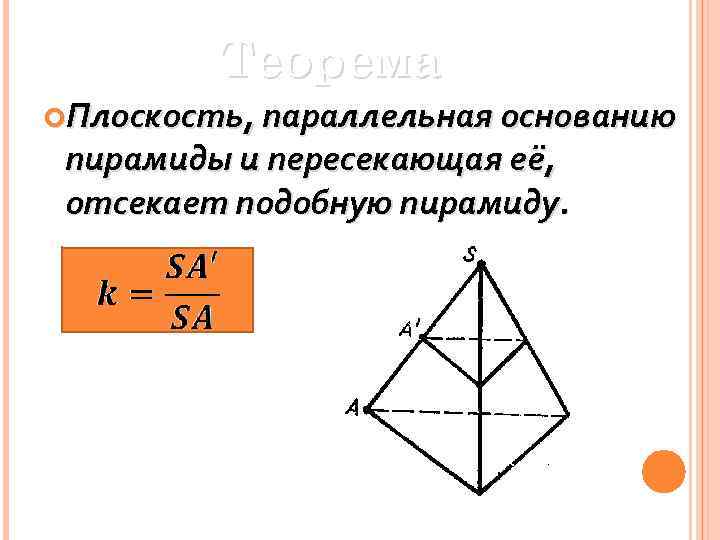Теорема Плоскость, параллельная основанию пирамиды и пересекающая её, отсекает подобную пирамиду. Теорема Плоскость, параллельная основанию пирамиды и пересекающая её, отсекает подобную пирамиду.

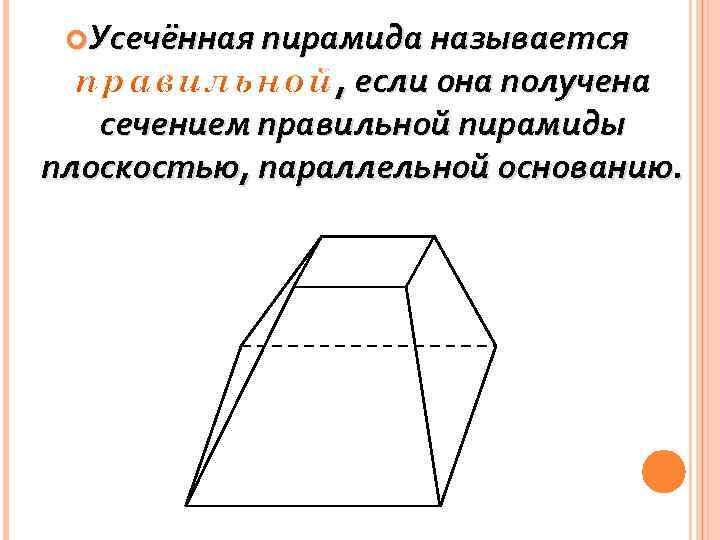Усечённая пирамида называется , если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Усечённая пирамида называется , если она получена сечением правильной пирамиды плоскостью, параллельной основанию.

Площадь боковой поверхности пирамиды Площадь боковой поверхности пирамиды

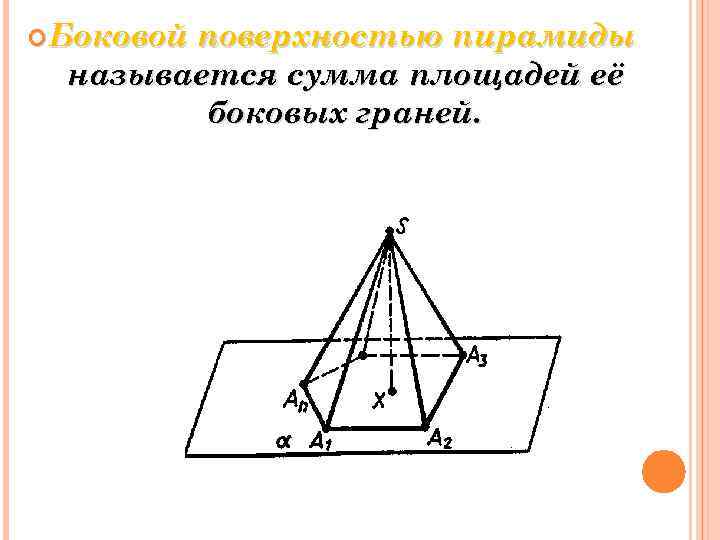Боковой поверхностью пирамиды называется сумма площадей её боковых граней. Боковой поверхностью пирамиды называется сумма площадей её боковых граней.

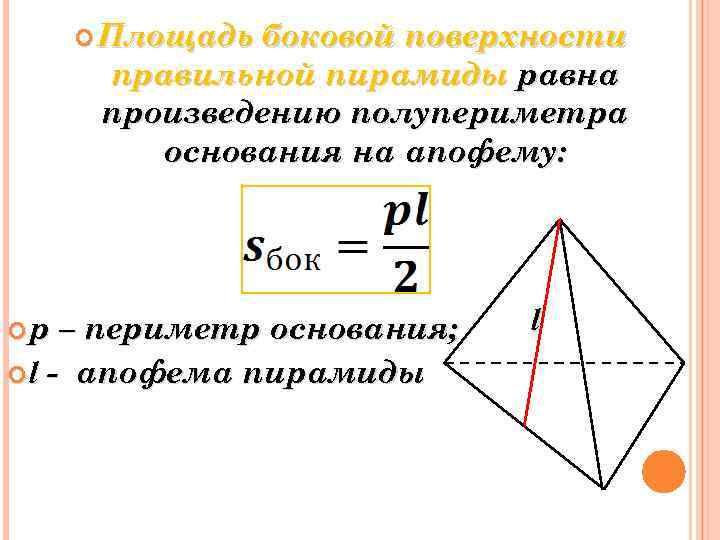Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на апофему: p – Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на апофему: p – периметр основания; l - апофема пирамиды l

Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему: Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему: p 1 и p 2 – периметры оснований; l - апофема пирамиды.

Задача Основание пирамиды – прямоугольник со сторонами 5 см и 9 см. Высота пирамиды 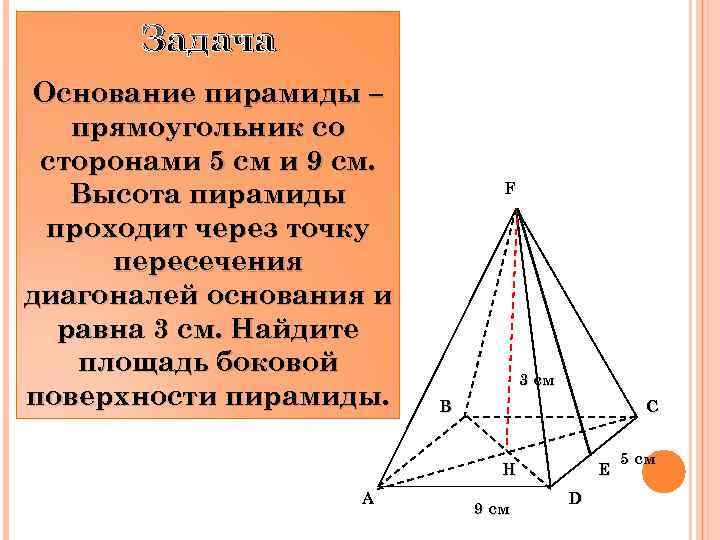Задача Основание пирамиды – прямоугольник со сторонами 5 см и 9 см. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 3 см. Найдите площадь боковой поверхности пирамиды. F 3 см B C Н A 9 см Е D 5 см

Площадь полной поверхности пирамиды Площадь полной поверхности пирамиды

Площадь полной поверхности правильной пирамиды равна сумме площади боковой поверхности и площади основания: Площадь полной поверхности правильной пирамиды равна сумме площади боковой поверхности и площади основания:

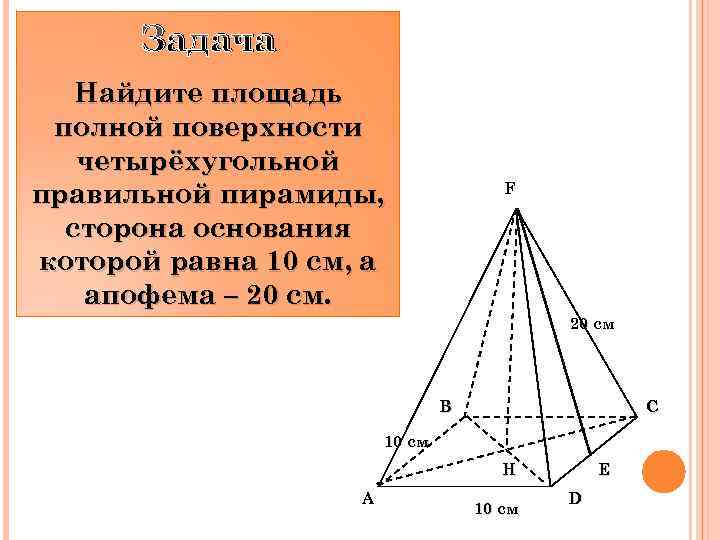Задача Найдите площадь полной поверхности четырёхугольной правильной пирамиды, сторона основания которой равна 10 см, Задача Найдите площадь полной поверхности четырёхугольной правильной пирамиды, сторона основания которой равна 10 см, а апофема – 20 см. F 20 см B C 10 см Н A 10 см Е D

Объём пирамиды Объём пирамиды

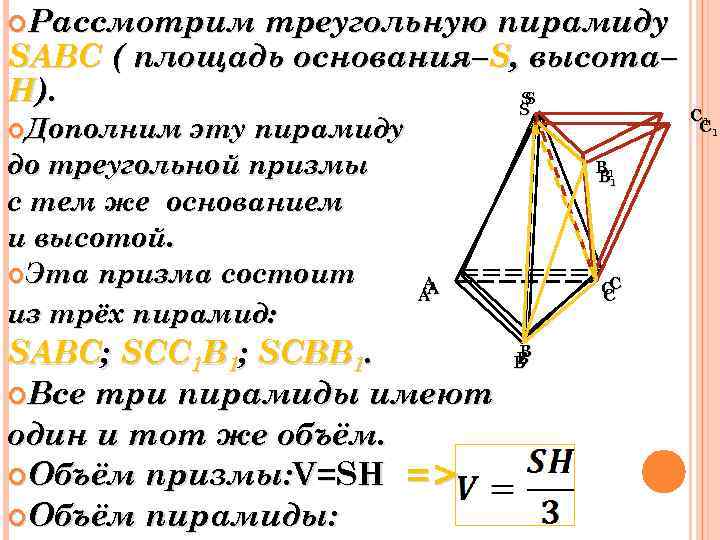Рассмотрим треугольную пирамиду SABC ( площадь основания–S, высота– H). S S S Дополним Рассмотрим треугольную пирамиду SABC ( площадь основания–S, высота– H). S S S Дополним эту пирамиду до треугольной призмы с тем же основанием и высотой. Эта призма состоит из трёх пирамид: B 1 A A A SABC; SCC 1 B 1; SCBB 1. Все три пирамиды имеют один и тот же объём. Объём призмы: V=SH => Объём пирамиды: С С С В В В C 1

Объём любой пирамиды равен одной трети произведения площади её основания на высоту: Объём любой пирамиды равен одной трети произведения площади её основания на высоту:

Объём усечённой пирамиды Объём усечённой пирамиды

Объём усечённой пирамиды с площадями оснований Q 1 и Q 2 и высотой Объём усечённой пирамиды с площадями оснований Q 1 и Q 2 и высотой H : Q 1 H Q 2

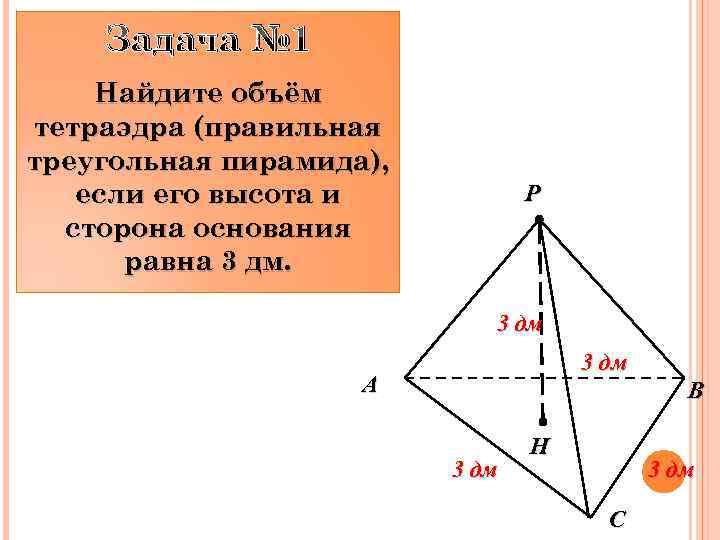Задача № 1 Найдите объём тетраэдра (правильная треугольная пирамида), если его высота и сторона Задача № 1 Найдите объём тетраэдра (правильная треугольная пирамида), если его высота и сторона основания равна 3 дм. P 3 дм A B 3 дм H 3 дм C

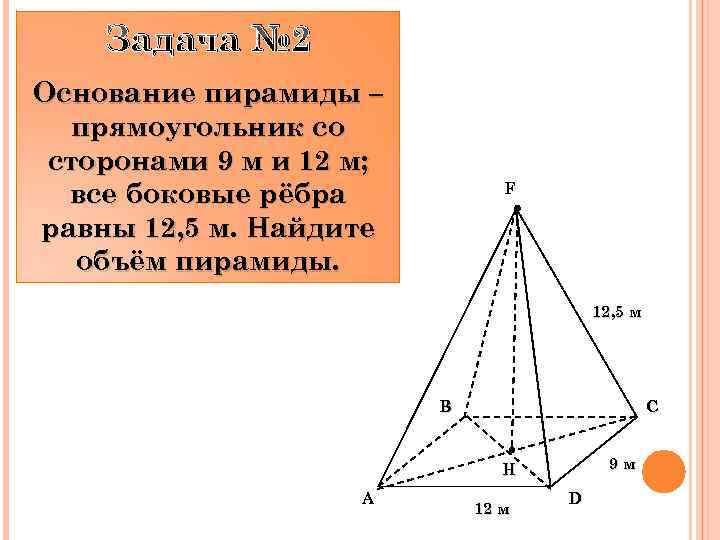Задача № 2 Основание пирамиды – прямоугольник со сторонами 9 м и 12 м; Задача № 2 Основание пирамиды – прямоугольник со сторонами 9 м и 12 м; все боковые рёбра равны 12, 5 м. Найдите объём пирамиды. F 12, 5 м B C 9 м Н A 12 м D

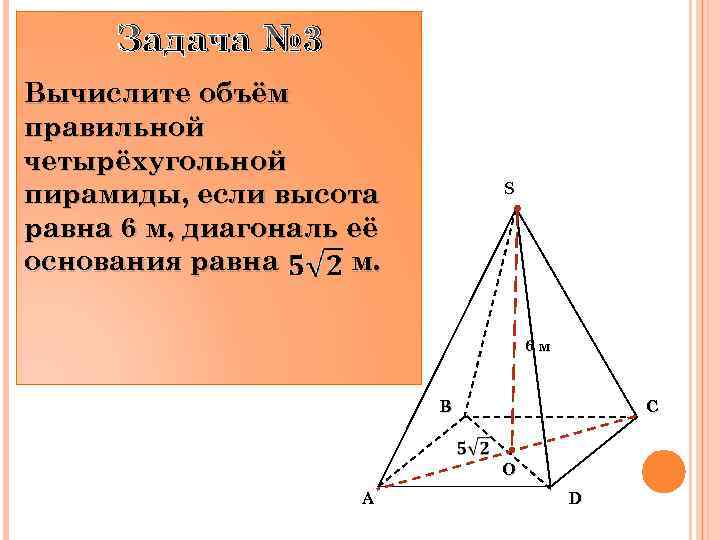Задача № 3 Вычислите объём правильной четырёхугольной пирамиды, если высота равна 6 м, диагональ Задача № 3 Вычислите объём правильной четырёхугольной пирамиды, если высота равна 6 м, диагональ её основания равна м. S 6 м B C O A D

Задача № 4 (д/з) Основание пирамиды прямоугольник со сторонами 6 см и 8 см. Задача № 4 (д/з) Основание пирамиды прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см, апофема – 12 см. Вычислите площадь боковой поверхности, площадь полной поверхности и объём пирамиды. К 13 см 12 см B C 6 м О Н A 8 м D

Зачёт по теме: «Пирамида» Зачёт по теме: «Пирамида»

ПЛАН ВЫПОЛНЕНИЯ РАБОТЫ: 1. Определить вид данной фигуры. 2. Определить необходимые измерения для уточнения ПЛАН ВЫПОЛНЕНИЯ РАБОТЫ: 1. Определить вид данной фигуры. 2. Определить необходимые измерения для уточнения вида фигуры. 3. Записать формулы вычисления периметра и площади основания данной фигуры. 4. Записать формулу вычисления боковой поверхности данной фигуры. 5. Записать формулу вычисления полной поверхности. 6. Записать формулу для вычисления объёма данной фигуры. 7. Произвести непосредственные измерения соответствующих элементов. 8. Вычислить периметр основания данной фигуры. 9. Вычислить площадь боковой поверхности фигуры. 10. Вычислить площадь основания данной фигуры. 11. Вычислить площадь полной поверхности фигуры.