Тема Основные законы распределения НСВ План 1 Равномерный

Тема. Основные законы распределения НСВ План: 1. Равномерный закон распределения. 2. Показательный закон распределения. 3. Нормальный закон распределения. лекция № 4 Постникова Ольга Алексеевна 1

При решении задач, которые выдвигает практика, приходится сталкиваться с различными распределениями непрерывных случайных величин. лекция № 4 Постникова Ольга Алексеевна 2

Плотности распределений непрерывных случайных величин называют также законами распределений. Часто встречаются законы равномерного, нормального и показательного распределений. лекция № 4 Постникова Ольга Алексеевна 3

1. Равномерный закон распределения Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение. лекция № 4 Постникова Ольга Алексеевна 4

НСВ считается распределенной, если вероятности имеет вид лекция № 4 Постникова Ольга Алексеевна равномерно ее плотность 5

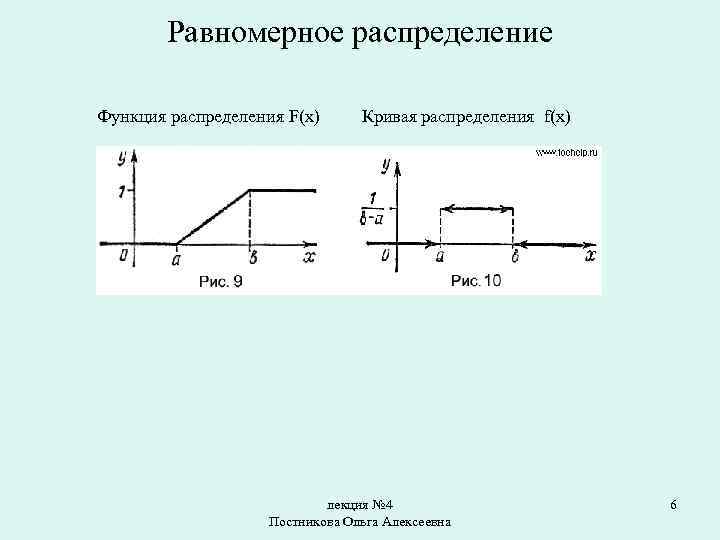Равномерное распределение Функция распределения F(x) Кривая распределения f(x) лекция № 4 Постникова Ольга Алексеевна 6

Числовые характеристики равномерно распределенной случайной величины находятся по следующим формулам: лекция № 4 Постникова Ольга Алексеевна 7

• Пример. Случайная величина распределена равномерно в интервале (2; 8). Найти ее математическое ожидание и дисперсию. • Решение. лекция № 4 Постникова Ольга Алексеевна 8

2. Показательный закон распределения Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью где - постоянная положительная величина. лекция № 4 Постникова Ольга Алексеевна 9

Показательное определяется одним параметром распределение. Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров. лекция № 4 Постникова Ольга Алексеевна 10

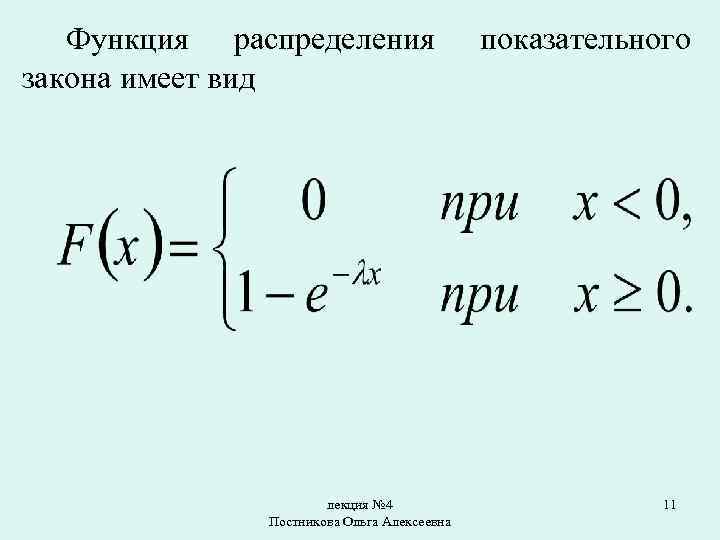Функция распределения закона имеет вид лекция № 4 Постникова Ольга Алексеевна показательного 11

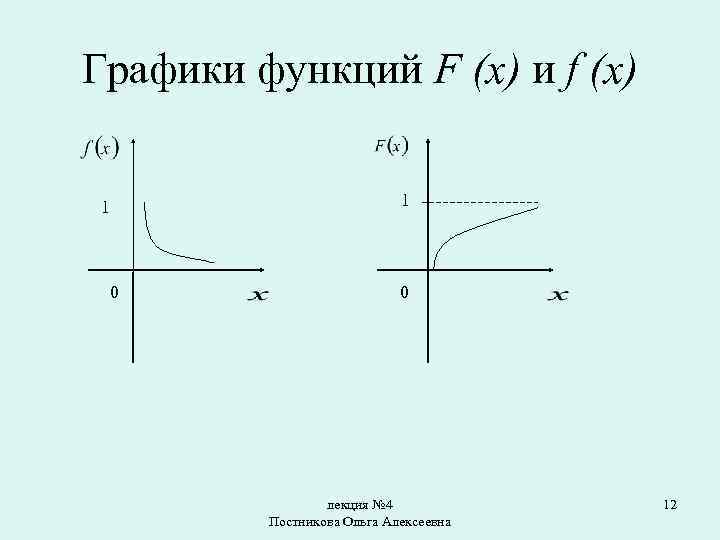Графики функций F (x) и f (x) 1 1 0 0 лекция № 4 Постникова Ольга Алексеевна 12

Вероятность попадания в заданный интервал показательно распределенной случайной величины Вероятность попадания в интервал непрерывной случайной величины X, которая распределена по показательному закону, заданному функцией распределения вычисляется по формуле лекция № 4 Постникова Ольга Алексеевна 13

Пример. Непрерывная случайная величина X распределена по показательному закону при ; при. Найти вероятность того, что в результате испытания X попадет в интервал (0, 3 ; 1). Решение. По условию, . лекция № 4 Постникова Ольга Алексеевна 14

Числовые характеристики показательного распределения Числовые характеристики непрерывной случайной величины X распределенной по показательному закону вычисляются по формулам: лекция № 4 Постникова Ольга Алексеевна 15

Пример. Непрерывная случайная величина X распределена по показательному закону при ; при. Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X. лекция № 4 Постникова Ольга Алексеевна 16

Пример. Непрерывная случайная величина X распределена по показательному закону при ; при. Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X. Решение. По условию, . Следовательно, лекция № 4 Постникова Ольга Алексеевна 17

3. Нормальный закон распределения Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью лекция № 4 Постникова Ольга Алексеевна 18

Нормальное распределение определяется двумя параметрами: Достаточно знать эти параметры, чтобы задать нормальное распределение. лекция № 4 Постникова Ольга Алексеевна 19

Нормальная кривая График плотности распределения называют кривой (кривой Гаусса). лекция № 4 Постникова Ольга Алексеевна нормального нормальной 20

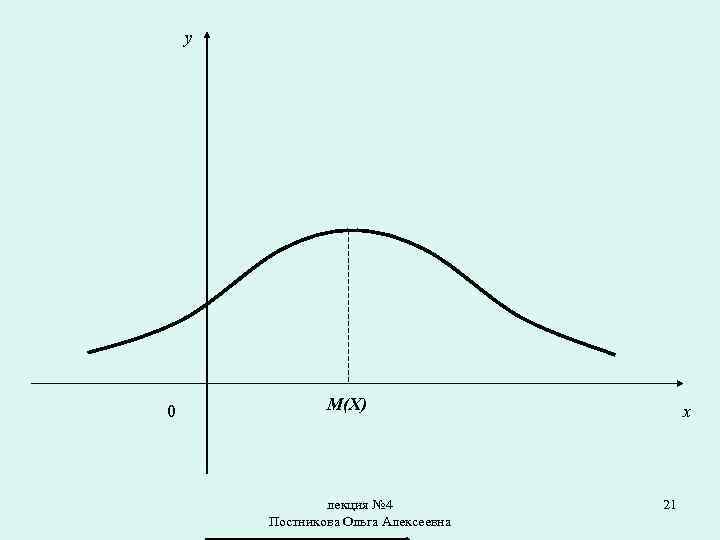y 0 M(X) лекция № 4 Постникова Ольга Алексеевна x 21

Влияние параметров нормального распределения на форму нормальной кривой. Изменение величины параметра не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси абсцисс: вправо, если математическое ожидание возрастает и влево, если оно убывает. лекция № 4 Постникова Ольга Алексеевна 22

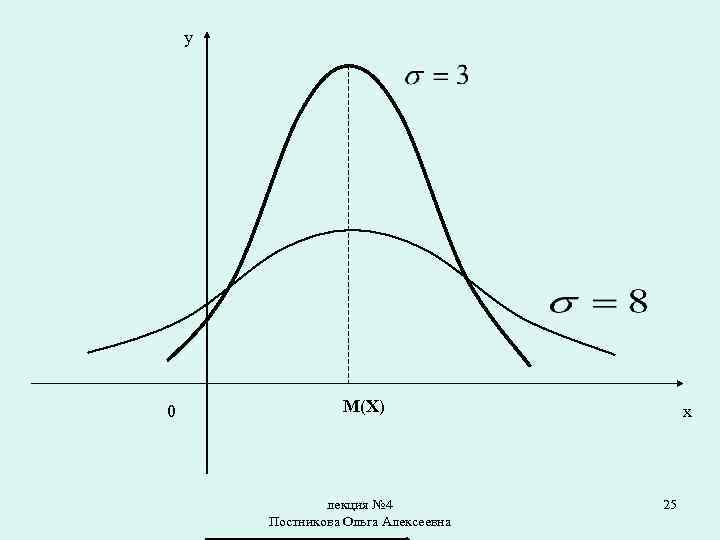
С возрастанием среднего квадратического отклонения максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т. е. сжимается к оси абсцисс. лекция № 4 Постникова Ольга Алексеевна 23

При убывании среднего квадратического отклонения нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси ординат. лекция № 4 Постникова Ольга Алексеевна 24

y 0 M(X) лекция № 4 Постникова Ольга Алексеевна x 25

При математическом ожидании равном нулю и среднем квадратическом отклонении равном единице нормальную кривую называют нормированной. лекция № 4 Постникова Ольга Алексеевна 26

Вероятность попадания в заданный интервал нормальной случайной величины Пусть случайная величина распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу , равна лекция № 4 Постникова Ольга Алексеевна 27

В результате преобразований и использования функции Лапласа лекция № 4 Постникова Ольга Алексеевна 28

окончательно получим лекция № 4 Постникова Ольга Алексеевна 29

Пример. Случайная величина X распределена по нормальному закону с математическим ожиданием равным 40 и средним квадратическим отклонением 30. Найти вероятность того, что X примет значение, принадлежащее интервалу (20; 70). лекция № 4 Постникова Ольга Алексеевна 30

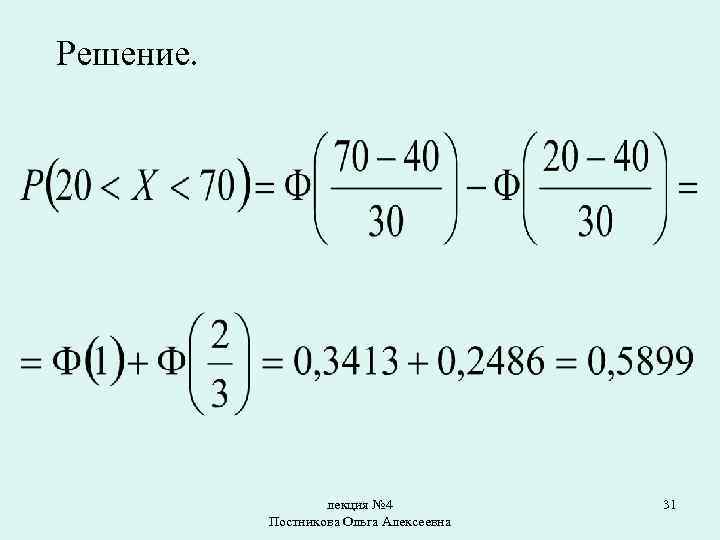Решение. лекция № 4 Постникова Ольга Алексеевна 31

Вычисление вероятности заданного отклонения • Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины по абсолютной величине меньше заданного положительного числа , т. е. найти вероятность осуществления неравенства лекция № 4 Постникова Ольга Алексеевна 32

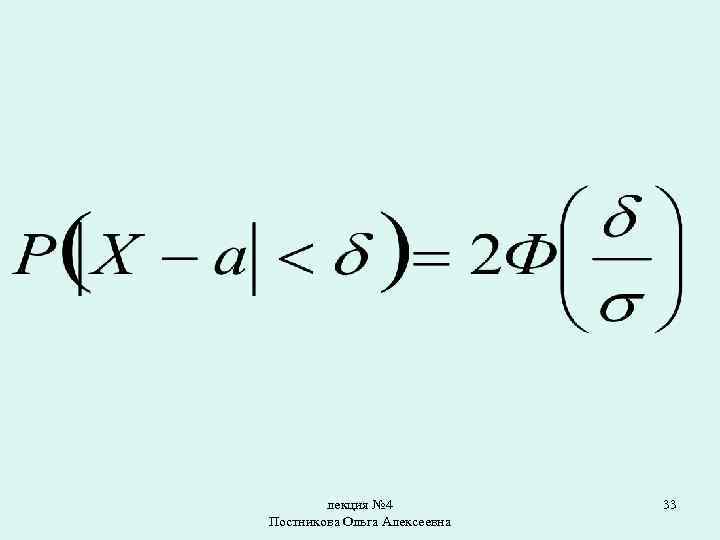лекция № 4 Постникова Ольга Алексеевна 33

• Пример. Случайная распределена нормально величина • Найти вероятность того, что отклонение по абсолютной величине будет меньше трех. лекция № 4 Постникова Ольга Алексеевна 34

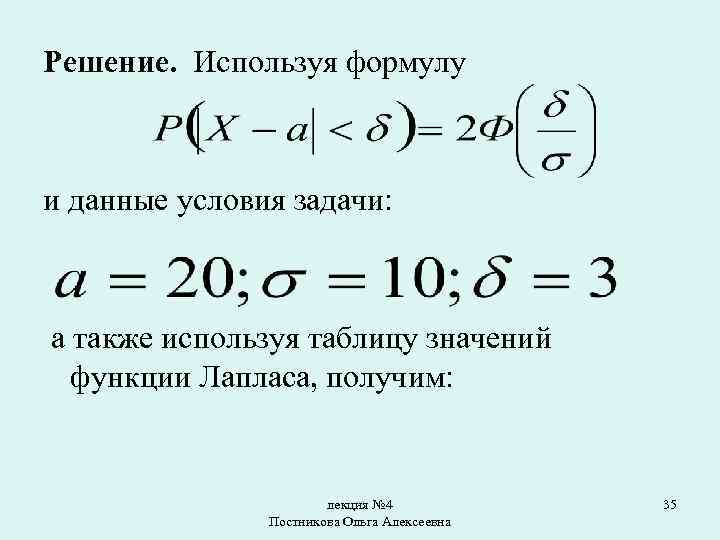Решение. Используя формулу и данные условия задачи: а также используя таблицу значений функции Лапласа, получим: лекция № 4 Постникова Ольга Алексеевна 35

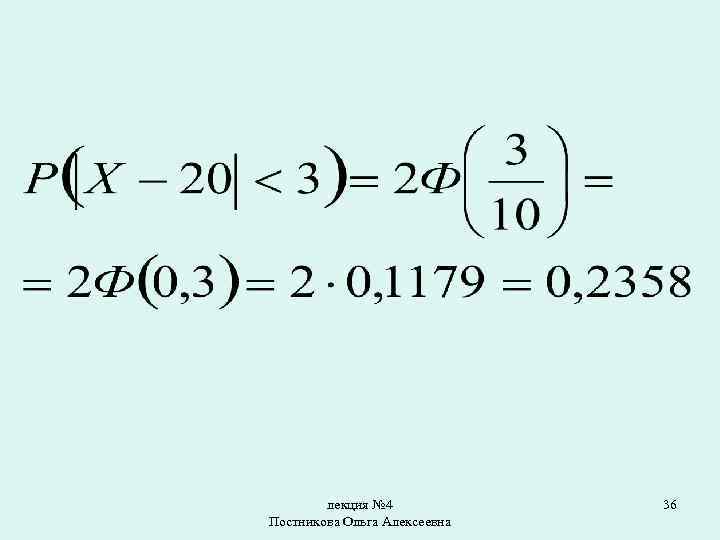лекция № 4 Постникова Ольга Алексеевна 36

Правило трех сигм: Если случайная величина имеет нормальный закон распределения с параметрами то практически достоверно (вероятность 0, 9973), что ее значения заключены в интервале лекция № 4 Постникова Ольга Алексеевна 37

На практике правило трех сигм применяют так: если распределение изучаемой величины неизвестно, но условие, указанное в правиле выполняется, то есть основание предполагать, что изучаемая величина распределена нормально. лекция № 4 Постникова Ольга Алексеевна 38