Системне повторення план_метр__..ppt
- Количество слайдов: 105
 Тема: Організація систематичного повторення планіметрії при підготовці до зовнішнього незалежного оцінювання
Тема: Організація систематичного повторення планіметрії при підготовці до зовнішнього незалежного оцінювання
 На нашу думку, повторення повинно бути: • • цілеспрямоване; обгрунтоване; з підвищенням рівня складності із змінюванням сенсорно-півкульного навантаження; як відтворювальним, так із застосуванням пошукової діяльності; активним; диференційованим; повним.
На нашу думку, повторення повинно бути: • • цілеспрямоване; обгрунтоване; з підвищенням рівня складності із змінюванням сенсорно-півкульного навантаження; як відтворювальним, так із застосуванням пошукової діяльності; активним; диференційованим; повним.
 Планіметрія
Планіметрія
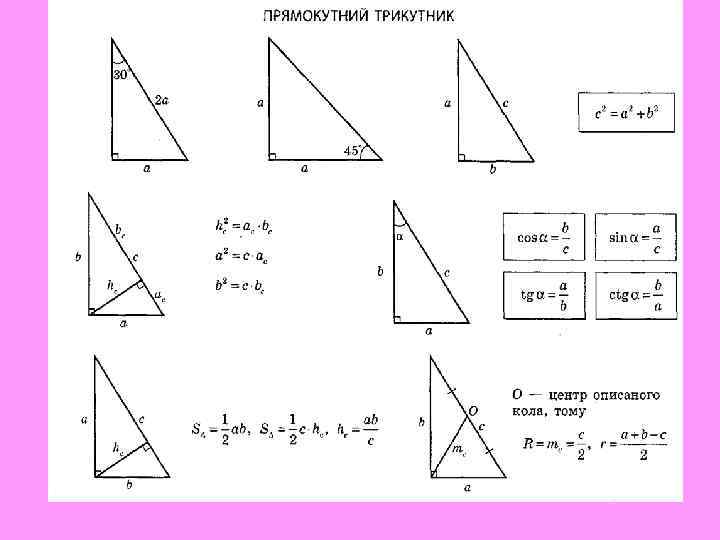
 Гіпотенуза прямокутного трикутника дорівнюнює 8 см, а катет — 4 см. Знайти: 1) другий катет трикутника; 2) медіану, проведену до гіпотенузи; 3) висоту, проведену на гіпотенузу.
Гіпотенуза прямокутного трикутника дорівнюнює 8 см, а катет — 4 см. Знайти: 1) другий катет трикутника; 2) медіану, проведену до гіпотенузи; 3) висоту, проведену на гіпотенузу.
 Катети прямокутного трикутника дорівнюють 6 см і 8 см. Знайти: 1) радіус описаного кола; 2) радіус вписаного кола; 3) площу трикутника.
Катети прямокутного трикутника дорівнюють 6 см і 8 см. Знайти: 1) радіус описаного кола; 2) радіус вписаного кола; 3) площу трикутника.
 Гіпотенуза прямокутного трикутника дорівнює 12 см, гострй кут 30 о. Знайти: 1) протилежний катет; 2) проекцію цього катета на гіпотенузу; 3) висоту, проведену на гіпотенузу.
Гіпотенуза прямокутного трикутника дорівнює 12 см, гострй кут 30 о. Знайти: 1) протилежний катет; 2) проекцію цього катета на гіпотенузу; 3) висоту, проведену на гіпотенузу.
 Катет прямокутного трикутника дорівнює 5 см, його проекція на гіпотенузу 2 см. Знайти: 1) гіпотенузу трикутника; 2) проекцію другого катета на гіпотенузу; 3) висоту, проведену на гіпотенузу.
Катет прямокутного трикутника дорівнює 5 см, його проекція на гіпотенузу 2 см. Знайти: 1) гіпотенузу трикутника; 2) проекцію другого катета на гіпотенузу; 3) висоту, проведену на гіпотенузу.
 Висота
Висота
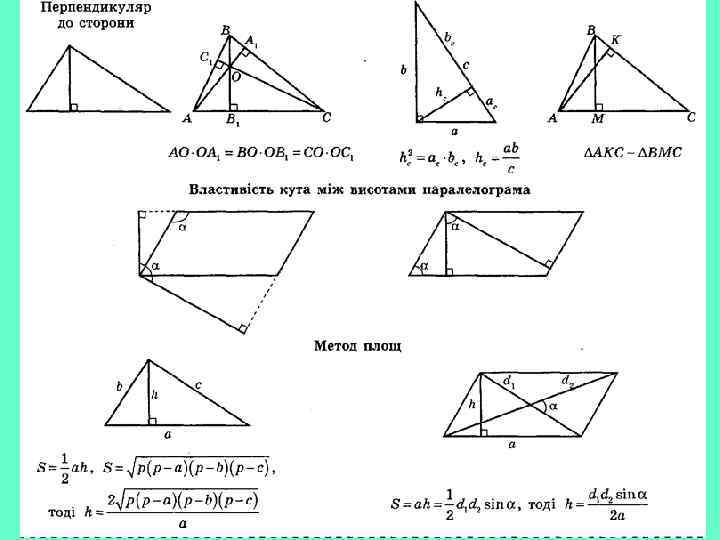
 Сторони трикутника дорівнюють 3 см, 4 см і 5 см. Знайти висоту проведену на більшу сторону трикутника.
Сторони трикутника дорівнюють 3 см, 4 см і 5 см. Знайти висоту проведену на більшу сторону трикутника.
 У прямокутному трикутнику гіпотенуза дорівнює 10 см, а проекція катета на гіпотенузу – 2 см. Знайти: 1. висоту, проведену на гіпотенузу; 2. катети трикутника.
У прямокутному трикутнику гіпотенуза дорівнює 10 см, а проекція катета на гіпотенузу – 2 см. Знайти: 1. висоту, проведену на гіпотенузу; 2. катети трикутника.
 У прямокутному трикутнику гіпотенуза дорівнює 10 см, а висота, проведена на гіпотенузу, 2 см. Знайти: 1) проекції катетів на гіпотенузу; 2) катети трикутника;
У прямокутному трикутнику гіпотенуза дорівнює 10 см, а висота, проведена на гіпотенузу, 2 см. Знайти: 1) проекції катетів на гіпотенузу; 2) катети трикутника;
 У трикутнику АВС проведено висоти АК і BD. СВ= 10 см, АС= 6 см, КС= 2 см. Знайти АD, якщо АВС – гострокутний трикутник.
У трикутнику АВС проведено висоти АК і BD. СВ= 10 см, АС= 6 см, КС= 2 см. Знайти АD, якщо АВС – гострокутний трикутник.
 Один із кутів паралелограма дорівнює 20 о. Знайти кут між висотами, проведеними з вершин тупого кута.
Один із кутів паралелограма дорівнює 20 о. Знайти кут між висотами, проведеними з вершин тупого кута.
 Сторони паралелограма дорівнюють 3 см і 8 см. Знайти більшу висоту паралелограма, якщо довжина меншої висоти 2 см.
Сторони паралелограма дорівнюють 3 см і 8 см. Знайти більшу висоту паралелограма, якщо довжина меншої висоти 2 см.
 Основи трапеції дорівнюють 2 см і 18 см, а діагоналі – 10 см і 12 см. Знайти висоту трапеції, проведену до основи, якщо кут між діагоналями дорівнює 135 о.
Основи трапеції дорівнюють 2 см і 18 см, а діагоналі – 10 см і 12 см. Знайти висоту трапеції, проведену до основи, якщо кут між діагоналями дорівнює 135 о.
 О – точка перетину висот АК, BD і CM трикутника АВС. АО= 5 см, ОМ= 4 см, ОК= 2 см. Знайти ОС.
О – точка перетину висот АК, BD і CM трикутника АВС. АО= 5 см, ОМ= 4 см, ОК= 2 см. Знайти ОС.
 Медіана
Медіана
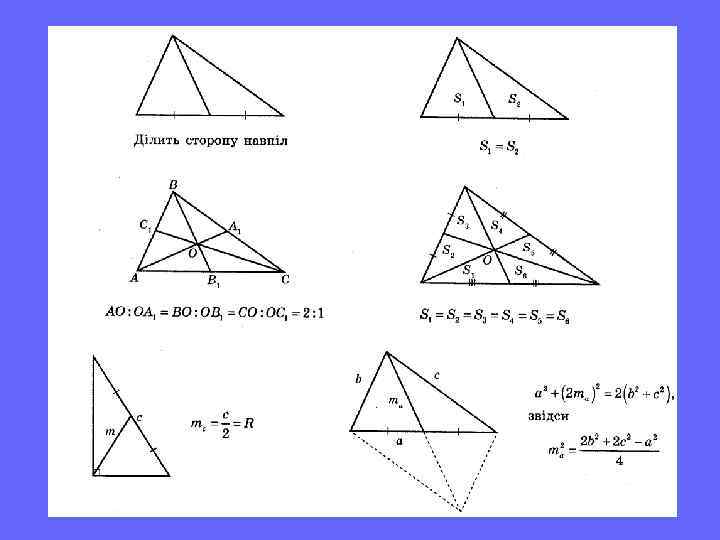
 У трикутнику АВС точка М – середина відрізка АС, точка N – середина відрізка ВС. Площа трикутника АВС дорівнює 20 см 2. Знайти площу трикутника BMN.
У трикутнику АВС точка М – середина відрізка АС, точка N – середина відрізка ВС. Площа трикутника АВС дорівнює 20 см 2. Знайти площу трикутника BMN.
 У трикутнику АВС О – точка перетину медіани АМ, BN і CK. Знайти ВО, ОМ і СК, якщо ОN = 2 см, АО = 3 см, ОС = 5 см.
У трикутнику АВС О – точка перетину медіани АМ, BN і CK. Знайти ВО, ОМ і СК, якщо ОN = 2 см, АО = 3 см, ОС = 5 см.
 Сторони трикутника дорівнюють 3 см, 5 см, 7 см. Знайти медіану трикутника, проведену до найбільшої сторони.
Сторони трикутника дорівнюють 3 см, 5 см, 7 см. Знайти медіану трикутника, проведену до найбільшої сторони.
 Катети прямокутного трикутника дорівнюють 3 см, 4 см. Знайти медіану, проведену до гіпотенузи.
Катети прямокутного трикутника дорівнюють 3 см, 4 см. Знайти медіану, проведену до гіпотенузи.
 У трикутнику АВС точка О – точка перетину медіан АМ, ВN і СК. Площа трикутника АОN дорівнює 8 см 2. Знайти площу трикутника АВС.
У трикутнику АВС точка О – точка перетину медіан АМ, ВN і СК. Площа трикутника АОN дорівнює 8 см 2. Знайти площу трикутника АВС.
 АМ – медіана трикутника АВС, МК – медіана трикутника АМВ, KD – медіана трикутника BKM, DE – медіана трикутника BKD. Знайти площу трикутника АВС, якщо площа трикутника BED дорівнює 10 см 2.
АМ – медіана трикутника АВС, МК – медіана трикутника АМВ, KD – медіана трикутника BKM, DE – медіана трикутника BKD. Знайти площу трикутника АВС, якщо площа трикутника BED дорівнює 10 см 2.
 У трикутнику АВС точка О – точка перетину медіан АМ, ВN і СК. АВ = 8 см, ВС = 16 см, АС = 12 см. Знайти площу трикутника NKM.
У трикутнику АВС точка О – точка перетину медіан АМ, ВN і СК. АВ = 8 см, ВС = 16 см, АС = 12 см. Знайти площу трикутника NKM.
 У прямокутному трикутнику медіана, проведена до гіпотенузи, дорівнює 8 см, а катет – 3 см. Знайти другий катет.
У прямокутному трикутнику медіана, проведена до гіпотенузи, дорівнює 8 см, а катет – 3 см. Знайти другий катет.
 Бісектриса
Бісектриса
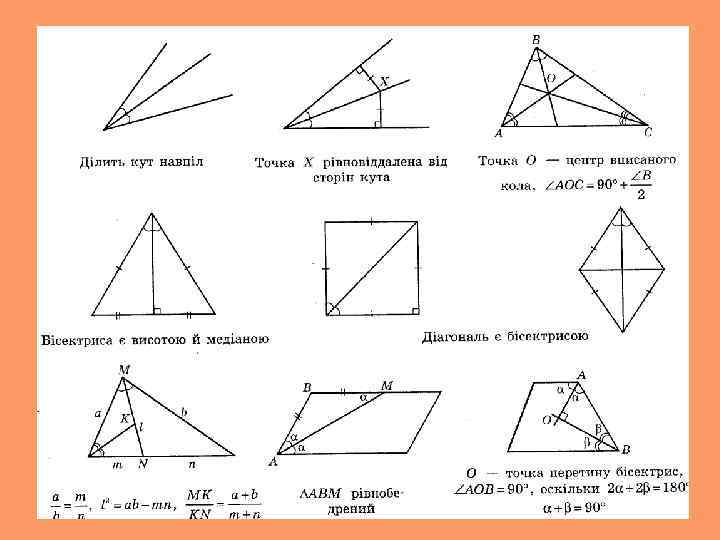
 Точка М рівновіддалена від сторін кута АВС. Знайти градусну міру кута АВС, якщо = 40 о.
Точка М рівновіддалена від сторін кута АВС. Знайти градусну міру кута АВС, якщо = 40 о.
 Трикутник АВС рівнобедрений, АВ=ВС. Точка М – середина відрізка АС. Знайти , якщо = 20 о.
Трикутник АВС рівнобедрений, АВ=ВС. Точка М – середина відрізка АС. Знайти , якщо = 20 о.
 АВСВ – квадрат, О – точка перетину діагоналей, АС = 10 см. Знайти: 1. 2. OD 3. AD
АВСВ – квадрат, О – точка перетину діагоналей, АС = 10 см. Знайти: 1. 2. OD 3. AD
 ABCD – ромб, ОМ – радіус вписаного кола, ОМ = 5 см, більша діагональ BD дорівнює 20 см. Знайти: 1) кути ромба; 2) сторону ромба; 3) діагональ АС.
ABCD – ромб, ОМ – радіус вписаного кола, ОМ = 5 см, більша діагональ BD дорівнює 20 см. Знайти: 1) кути ромба; 2) сторону ромба; 3) діагональ АС.
 АМ – бісектриса кута А паралелограма ABCD, М ВС. Знайти периметр паралелограма ABCD, якщо 1) ВМ = 5 см, МС = 2 см; 2) ВМ = 2 см, МС = 5 см.
АМ – бісектриса кута А паралелограма ABCD, М ВС. Знайти периметр паралелограма ABCD, якщо 1) ВМ = 5 см, МС = 2 см; 2) ВМ = 2 см, МС = 5 см.
 У трикутнику ABC проведено бісектрису ВМ, АВ = 5 см, ВС = 8 см, АМ = 2 см. Знайти: 1) МС; 2) ВМ.
У трикутнику ABC проведено бісектрису ВМ, АВ = 5 см, ВС = 8 см, АМ = 2 см. Знайти: 1) МС; 2) ВМ.
 У трикутнику АВС АВ: ВС = 2: 3, АС = 10 см, ВК – бісектриса. Знайти АК.
У трикутнику АВС АВ: ВС = 2: 3, АС = 10 см, ВК – бісектриса. Знайти АК.
 Дано трапецію ABCD, ОМ – радіус вписаного кола. Знайти ОМ, якщо СМ = 3 см, МD = 6 см (М СD).
Дано трапецію ABCD, ОМ – радіус вписаного кола. Знайти ОМ, якщо СМ = 3 см, МD = 6 см (М СD).
 Довільний трикутник
Довільний трикутник
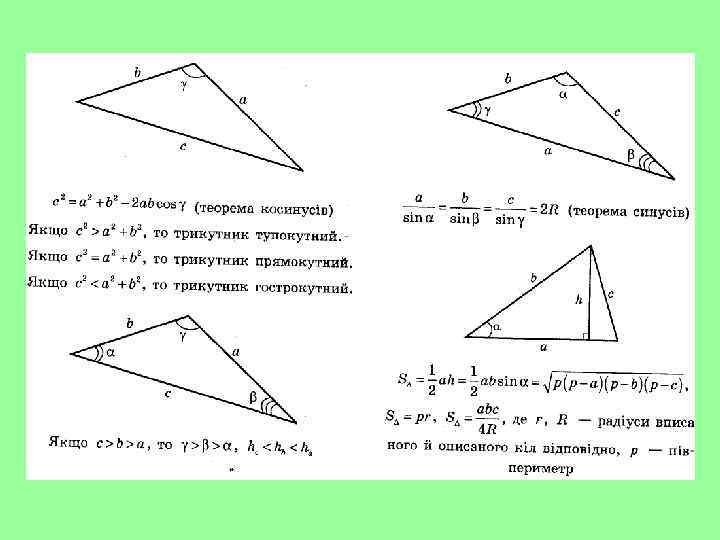
 Дві сторони трикутника дорівнюють 6 см і 8 см, а кут між ними 60 о. Знайти третю сторону трикутника.
Дві сторони трикутника дорівнюють 6 см і 8 см, а кут між ними 60 о. Знайти третю сторону трикутника.
 Сторони трикутника дорівнюють 4 см, 7 см, 10 см. Знайти найбільший кут трикутника.
Сторони трикутника дорівнюють 4 см, 7 см, 10 см. Знайти найбільший кут трикутника.
 У трикутнику АВС АВ =4 С = 45 о, А = 30 о. Знайти: 1. сторону ВС; 2. радіус описаного кола. см,
У трикутнику АВС АВ =4 С = 45 о, А = 30 о. Знайти: 1. сторону ВС; 2. радіус описаного кола. см,
 Сторони трикутника дорівнюють 2 дм, 5 дм, 6 дм. Визначити вид трикутника.
Сторони трикутника дорівнюють 2 дм, 5 дм, 6 дм. Визначити вид трикутника.
 У трикутнику АВС проведено висоти АА 1, ВВ 1, СС 1. АВ = 10 см, ВС = 15 см, АС = 8 см. Порівняти: 1. кути трикутника; 2. висоти трикутника.
У трикутнику АВС проведено висоти АА 1, ВВ 1, СС 1. АВ = 10 см, ВС = 15 см, АС = 8 см. Порівняти: 1. кути трикутника; 2. висоти трикутника.
 Дві сторони трикутника дорівнюють 2 см і 3 см, а кут між ними 30 о. Знайти площу трикутника.
Дві сторони трикутника дорівнюють 2 см і 3 см, а кут між ними 30 о. Знайти площу трикутника.
 Знайти площу трикутника, сторони якого дорівнюють 9 см, 10 см, 11 см.
Знайти площу трикутника, сторони якого дорівнюють 9 см, 10 см, 11 см.
 Сторони трикутника дорівнюють 6 см, 10 см, а рідіус описаного кола дорівнює. Знайти площу трикутника.
Сторони трикутника дорівнюють 6 см, 10 см, а рідіус описаного кола дорівнює. Знайти площу трикутника.
 Сторони трикутника дорівнюють 4 см, 5 см, 6 см. Знайти радіус вписаного кола.
Сторони трикутника дорівнюють 4 см, 5 см, 6 см. Знайти радіус вписаного кола.
 Кут при основі рівнобедреного трикутника дорівнює 30 о, а бічна сторона – 10 см. Знайти радіус описаного кола.
Кут при основі рівнобедреного трикутника дорівнює 30 о, а бічна сторона – 10 см. Знайти радіус описаного кола.
 Площа
Площа
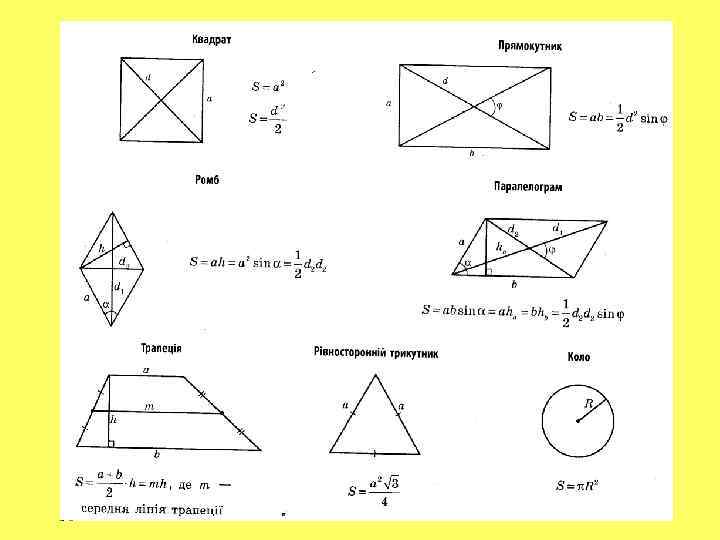
 У паралелограма ABCD АМ і АН – висоти, AM CD, АН СВ. Знайти площу паралелограма та висоту АН, якщо АВ = 15 см, ВС = 20 см, АМ = 8 см.
У паралелограма ABCD АМ і АН – висоти, AM CD, АН СВ. Знайти площу паралелограма та висоту АН, якщо АВ = 15 см, ВС = 20 см, АМ = 8 см.
 Знайти площу ромба, діагоналі якого дорівнюють 30 см і 12 см.
Знайти площу ромба, діагоналі якого дорівнюють 30 см і 12 см.
 Діагональ квадрата дорівнює 7 см. Знайти площу квадрата.
Діагональ квадрата дорівнює 7 см. Знайти площу квадрата.
 Знайти площу паралелограма, сторони якого дорівнюють 12 см і 20 см, а кут між ними 150 о.
Знайти площу паралелограма, сторони якого дорівнюють 12 см і 20 см, а кут між ними 150 о.
 Обчислити площу рівнобічної трапеції, основи якої дорівнюють 14 см і 6 см, а бічна сторона – 5 см.
Обчислити площу рівнобічної трапеції, основи якої дорівнюють 14 см і 6 см, а бічна сторона – 5 см.
 Знайти площу круга, діаметр якого дорівнює 10 см.
Знайти площу круга, діаметр якого дорівнює 10 см.
 Знайти площу прямокутника, якщо кут між його діагоналями 30 о, а діаметр описаного кола дорівнює 4 см.
Знайти площу прямокутника, якщо кут між його діагоналями 30 о, а діаметр описаного кола дорівнює 4 см.
 Знайти площу паралелограма, якщо його сторони дорівнюють см і 2 см, а висоти утворюють кут 60 о.
Знайти площу паралелограма, якщо його сторони дорівнюють см і 2 см, а висоти утворюють кут 60 о.
 Основи рівнобічної трапеції дорівнюють 17 см і 9 см, а кут між бічною основою і основою – 45 о. Знайти площу трапеції.
Основи рівнобічної трапеції дорівнюють 17 см і 9 см, а кут між бічною основою і основою – 45 о. Знайти площу трапеції.
 Знайти площу рівнобічної трапеції, висота якої дорівнює 7 см, а діагоналі взаємно перпендикулярні.
Знайти площу рівнобічної трапеції, висота якої дорівнює 7 см, а діагоналі взаємно перпендикулярні.
 Коло
Коло
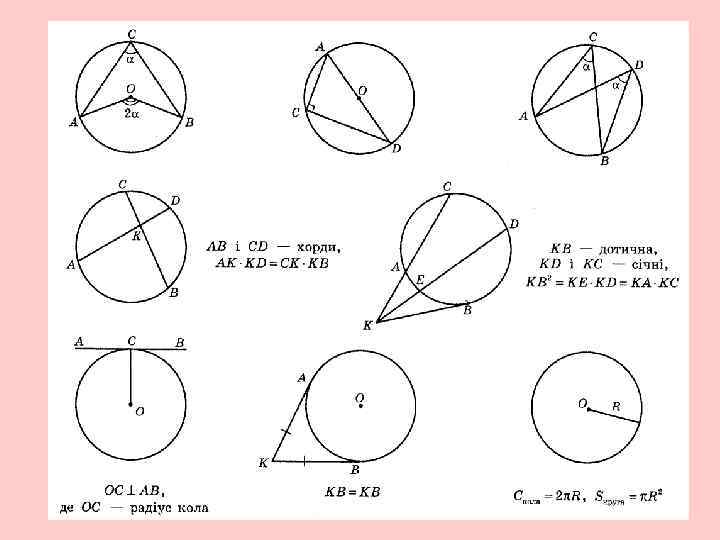
 Скільки градусів містить центральний кут кола, який спирається на дугу, що: 1. дорівнює 46 о; 2. становить кола?
Скільки градусів містить центральний кут кола, який спирається на дугу, що: 1. дорівнює 46 о; 2. становить кола?
 Знайти вписаний кут, якщо відповідний йому центральний кут дорівнює 28 о.
Знайти вписаний кут, якщо відповідний йому центральний кут дорівнює 28 о.
 Вписаний кут А спирається на дугу ВС і дорівнює 56 о. Знайти градусну міру вписаного кута М, який спирається на дугу ВС, якщо точки А і М розташовані: 1. з одного боку від хорди ВС; 2. по різні боки від хорди ВС.
Вписаний кут А спирається на дугу ВС і дорівнює 56 о. Знайти градусну міру вписаного кута М, який спирається на дугу ВС, якщо точки А і М розташовані: 1. з одного боку від хорди ВС; 2. по різні боки від хорди ВС.
 Знайти градусну міру вписаного кута, який спирається на діаметр.
Знайти градусну міру вписаного кута, який спирається на діаметр.
 Хорди АК і СВ перетинаються в точці D, що лежить усередині кола. АD = 5 см, DК = 16 см, DВ = 8 см. Знайти СD.
Хорди АК і СВ перетинаються в точці D, що лежить усередині кола. АD = 5 см, DК = 16 см, DВ = 8 см. Знайти СD.
 Хорди АК і СВ належать прямим, які перетинаються в точці D, що лежить поза колом (точка А належить відрізку DК, точка С належить відрізку DВ). DА = 5 см, АК = 7 см, DВ = 18 см. Знайти DС.
Хорди АК і СВ належать прямим, які перетинаються в точці D, що лежить поза колом (точка А належить відрізку DК, точка С належить відрізку DВ). DА = 5 см, АК = 7 см, DВ = 18 см. Знайти DС.
 З точки К поза колом проведено дотичну КА та січну КВ, яка перетинає коло в точці С. Знайти КА, якщо КС = 6 см, СВ = 9 см.
З точки К поза колом проведено дотичну КА та січну КВ, яка перетинає коло в точці С. Знайти КА, якщо КС = 6 см, СВ = 9 см.
 Діаметр кола дорівнює 10 см. Знайти довжину кола.
Діаметр кола дорівнює 10 см. Знайти довжину кола.
 Площа круга дорівнює 81 см 2. Знайти радіус круга.
Площа круга дорівнює 81 см 2. Знайти радіус круга.
 Знайти площу кругового сектора, що відповідає центральному куту 60 о, якщо радіус круга дорівнює 6 см.
Знайти площу кругового сектора, що відповідає центральному куту 60 о, якщо радіус круга дорівнює 6 см.
 Радіус вписаного кола
Радіус вписаного кола
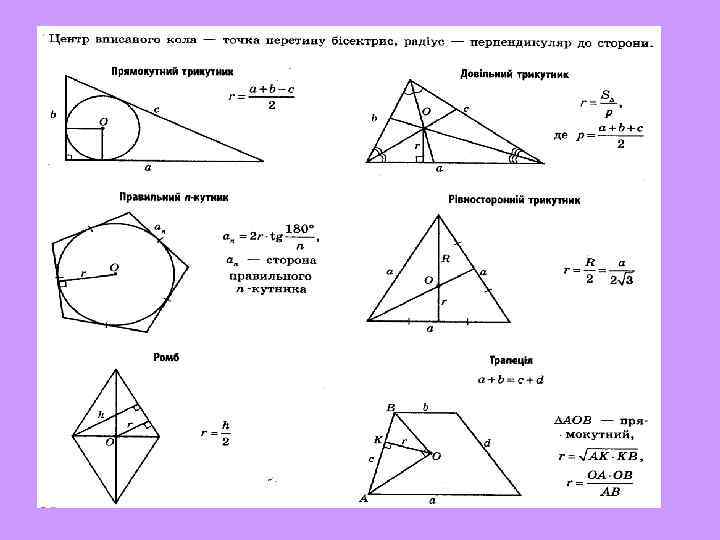
 Катети прямокутного трикутника дорівнюють 5 см і 10 см. Знайти радіус вписаного кола.
Катети прямокутного трикутника дорівнюють 5 см і 10 см. Знайти радіус вписаного кола.
 Сторони трикутника дорівнюють 10 см, 12 см і 8 см. Знайти радіус вписаного кола.
Сторони трикутника дорівнюють 10 см, 12 см і 8 см. Знайти радіус вписаного кола.
 Знайти радіус кола, вписаного в правильний п'ятикутник, сторона якого дорівнює 14 см.
Знайти радіус кола, вписаного в правильний п'ятикутник, сторона якого дорівнює 14 см.
 Знайти радіус кола, вписаного в рівносторонній трикутник, якщо радіус описаного кола 18 см.
Знайти радіус кола, вписаного в рівносторонній трикутник, якщо радіус описаного кола 18 см.
 Сторона ромба дорівнює 24 см, а гострий кут 30 о. Знайти радіус кола, вписаного в ромб.
Сторона ромба дорівнює 24 см, а гострий кут 30 о. Знайти радіус кола, вписаного в ромб.
 Чи можна вписати коло в чотирикутник, сторони якого дорівнюють 12 см, 15 см, 17 см, 8 см?
Чи можна вписати коло в чотирикутник, сторони якого дорівнюють 12 см, 15 см, 17 см, 8 см?
 ABCD – трапеція, у яку вписано коло. Знайти периметр трапеції, основи якої дорівнюють 6 см, 17 см.
ABCD – трапеція, у яку вписано коло. Знайти периметр трапеції, основи якої дорівнюють 6 см, 17 см.
 Коло, вписане в рівнобічну трапецію, дотикається до бічної сторони в точці, яка ділить бічну сторону на відрізки 16 см і 25 см. Знайти: 1. основи трапеції; 2. радіус вписаного кола.
Коло, вписане в рівнобічну трапецію, дотикається до бічної сторони в точці, яка ділить бічну сторону на відрізки 16 см і 25 см. Знайти: 1. основи трапеції; 2. радіус вписаного кола.
 Радіус описаного кола
Радіус описаного кола
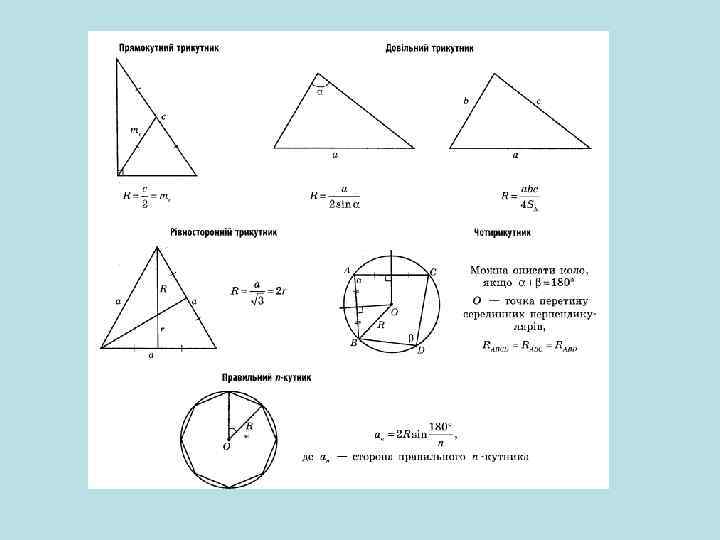
 Знайти радіус кола, описаного навколо прямокутного трикутника, катети якого дорівнюють 6 см і 8 см.
Знайти радіус кола, описаного навколо прямокутного трикутника, катети якого дорівнюють 6 см і 8 см.
 У трикутнику АВС АВ = 8 см, С = 45 о. Знайти радіус описаного кола
У трикутнику АВС АВ = 8 см, С = 45 о. Знайти радіус описаного кола
 Сторони трикутника дорівнюють 5 см, 6 см, 7 см. Знайти радіус описаного кола.
Сторони трикутника дорівнюють 5 см, 6 см, 7 см. Знайти радіус описаного кола.
 Радіус кола, описаного навколо рівностороннього трикутника, дорівнює 15 см. Знайти радіус вписаного кола.
Радіус кола, описаного навколо рівностороннього трикутника, дорівнює 15 см. Знайти радіус вписаного кола.
 Сторона правильного восьмикутника дорівнює 20 см. Знайти радіус описаного кола.
Сторона правильного восьмикутника дорівнює 20 см. Знайти радіус описаного кола.
 Чи можна описати коло навколо чотирикутника АВСD, якщо кут А дорівнює 20 о, а кут С дорівнює 160 о?
Чи можна описати коло навколо чотирикутника АВСD, якщо кут А дорівнює 20 о, а кут С дорівнює 160 о?
 Навколо чотирикутника АВСD описано коло, А = 10 о, В = 100 о. Знайти: 1. кут С; 2. кут D.
Навколо чотирикутника АВСD описано коло, А = 10 о, В = 100 о. Знайти: 1. кут С; 2. кут D.
 Знайти радіус кола, описаного навколо чотирикутника ABCD, якщо його діагональ АС дорівнює 15 см, АВС = 120 о
Знайти радіус кола, описаного навколо чотирикутника ABCD, якщо його діагональ АС дорівнює 15 см, АВС = 120 о
 Декартова система координат. Вектори
Декартова система координат. Вектори

 А (2; -3), В (-5; -4). Знайти: 1. Координати середини відрізка АВ; 2. Довжину відрізка АВ; 3. Рівняння прямої АВ.
А (2; -3), В (-5; -4). Знайти: 1. Координати середини відрізка АВ; 2. Довжину відрізка АВ; 3. Рівняння прямої АВ.
 Записати рівняння прямої, яка нахилена до осі абсцис під кутом 45 о і проходить через точку А (4; -2).
Записати рівняння прямої, яка нахилена до осі абсцис під кутом 45 о і проходить через точку А (4; -2).
 Записати рівняння кола, якщо радіус кола дорівнює 3 см, а координати центра (-2; 5).
Записати рівняння кола, якщо радіус кола дорівнює 3 см, а координати центра (-2; 5).
 АВ – діаметр кола, А (-6; -4), В (2; 0). Знайти: 1. координати центра кола; 2. радіус кола; 3. рівняння кола.
АВ – діаметр кола, А (-6; -4), В (2; 0). Знайти: 1. координати центра кола; 2. радіус кола; 3. рівняння кола.
 А (2; 3), В (3; -3). Знайти: 1. Координати вектора ; 2. Модуль вектора ; 3. Координати вектора.
А (2; 3), В (3; -3). Знайти: 1. Координати вектора ; 2. Модуль вектора ; 3. Координати вектора.
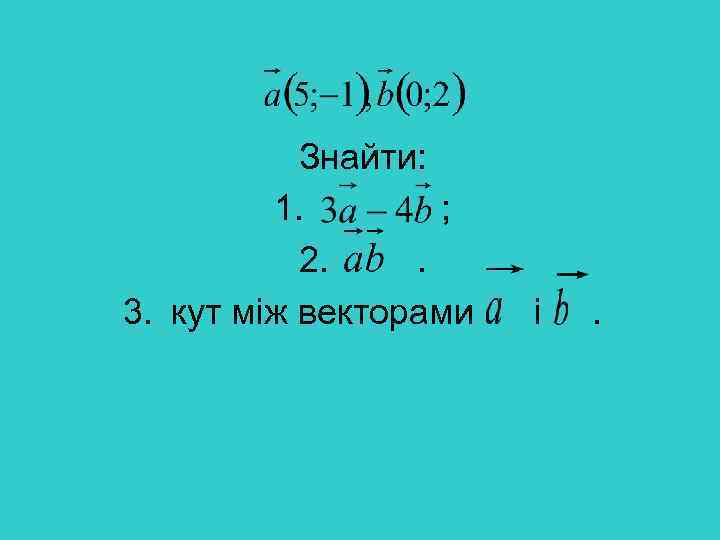 Знайти: 1. ; 2. . 3. кут між векторами і .
Знайти: 1. ; 2. . 3. кут між векторами і .
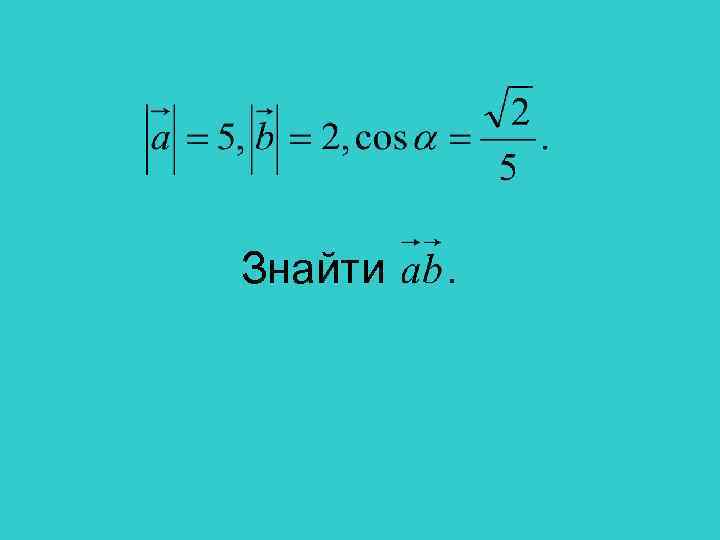 Знайти .
Знайти .
 Знайти.
Знайти.
 Дякую за увагу!
Дякую за увагу!


