Презентация многогранники.pptx
- Количество слайдов: 32
 Тема: Многогранники.
Тема: Многогранники.
 История Правильные многогранники с древних времен привлекали к себе внимание ученых, строителей, архитекторов и многих других. Их поражала красота, совершенство, гармония этих многогранников. Пифагорейцы считали их божественными и использовали в свих философских сочинениях о существе мира.
История Правильные многогранники с древних времен привлекали к себе внимание ученых, строителей, архитекторов и многих других. Их поражала красота, совершенство, гармония этих многогранников. Пифагорейцы считали их божественными и использовали в свих философских сочинениях о существе мира.
 Платон • Подробно описал свойства правильных многогранников, поэтому многогранники называют телами Платона. • Платоновыми телами называют правильные однородные выпуклые многогранники. • Платоновы тела-трехмерный аналог плоских правильных многоугольников. Платон (429 – 348 до н. э)
Платон • Подробно описал свойства правильных многогранников, поэтому многогранники называют телами Платона. • Платоновыми телами называют правильные однородные выпуклые многогранники. • Платоновы тела-трехмерный аналог плоских правильных многоугольников. Платон (429 – 348 до н. э)
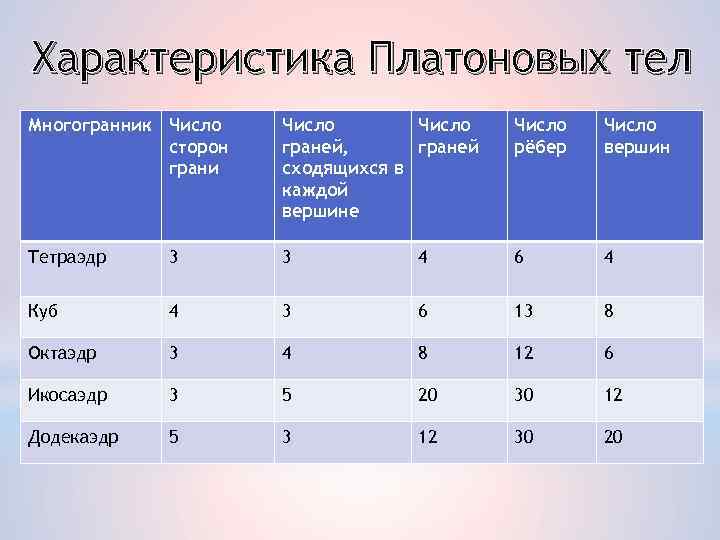 Характеристика Платоновых тел Многогранник Число сторон грани Число граней, граней сходящихся в каждой вершине Число рёбер Число вершин Тетраэдр 3 3 4 6 4 Куб 4 3 6 13 8 Октаэдр 3 4 8 12 6 Икосаэдр 3 5 20 30 12 Додекаэдр 5 3 12 30 20
Характеристика Платоновых тел Многогранник Число сторон грани Число граней, граней сходящихся в каждой вершине Число рёбер Число вершин Тетраэдр 3 3 4 6 4 Куб 4 3 6 13 8 Октаэдр 3 4 8 12 6 Икосаэдр 3 5 20 30 12 Додекаэдр 5 3 12 30 20
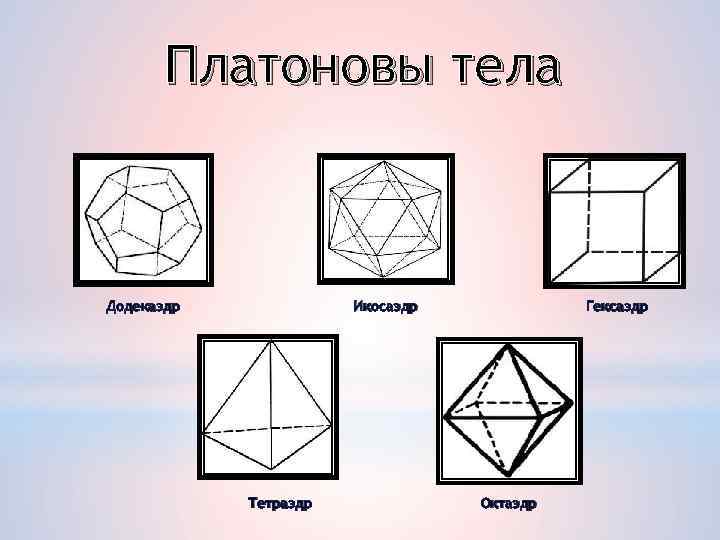 Платоновы тела Додекаэдр Икосаэдр Тетраэдр Гексаэдр Октаэдр
Платоновы тела Додекаэдр Икосаэдр Тетраэдр Гексаэдр Октаэдр
 Леонардо Да Винчи Леноардо Да Винчи- скульптор, архитектор, художники. • Увлекался теорией многогранников и часто изображал их на своих полотнах. • Проиллюстрировал изображениями правильных и полуправильных многогранников книгу своего друга « О Божественной пропорции» Леонардо Да Винчи
Леонардо Да Винчи Леноардо Да Винчи- скульптор, архитектор, художники. • Увлекался теорией многогранников и часто изображал их на своих полотнах. • Проиллюстрировал изображениями правильных и полуправильных многогранников книгу своего друга « О Божественной пропорции» Леонардо Да Винчи
 Ycocedron Abscisus Vacuus. • Ycocedron Abscisus – Усеченный икосаэдр • Термин Vacuus – обозначает тот факт, что грани многогранника изображены «пустыми» -не сплошными.
Ycocedron Abscisus Vacuus. • Ycocedron Abscisus – Усеченный икосаэдр • Термин Vacuus – обозначает тот факт, что грани многогранника изображены «пустыми» -не сплошными.
 Альберт Дюрер • Альберт Дюрер-знаменитый художник эпохи Возрождения. • Увлекался геометрий • В его известной гравюре «Меланхолия» был изображен додекаэдр. • В 1525 году Дюрер написал трактат, в котором представил 5 правильных многогранников, поверхности которых служат хорошими моделями перспективы.
Альберт Дюрер • Альберт Дюрер-знаменитый художник эпохи Возрождения. • Увлекался геометрий • В его известной гравюре «Меланхолия» был изображен додекаэдр. • В 1525 году Дюрер написал трактат, в котором представил 5 правильных многогранников, поверхности которых служат хорошими моделями перспективы.
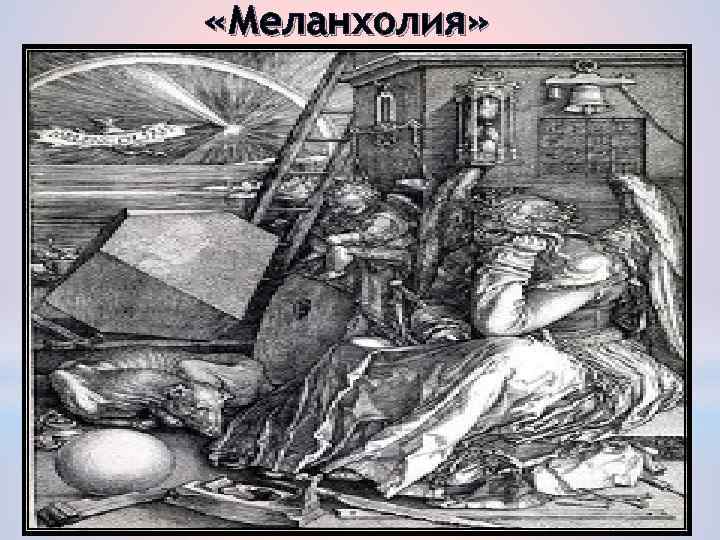 «Меланхолия»
«Меланхолия»
 Космологическая гипотеза Кеплера Иоганн Кеплер (1571 -1630) в своей работе в 1596 году, используя правильные многоугольники, вывел принцип, которому подчиняются формы и размеры орбит планет Солнечной системы. Он пытался связать некоторые свойства Солнечной системы со свойствами правильных многогранников.
Космологическая гипотеза Кеплера Иоганн Кеплер (1571 -1630) в своей работе в 1596 году, используя правильные многоугольники, вывел принцип, которому подчиняются формы и размеры орбит планет Солнечной системы. Он пытался связать некоторые свойства Солнечной системы со свойствами правильных многогранников.
 Многогранники в стереометрии. Стереометрия-раздел геометрии, в котором изучаются свойства фигур в пространстве (пространственных фигур). Слово «стереометрия» состоит из греческих слов «стереос» – телесный, пространственный и «метрео» измеряю. Многогранники могут быть выпуклыми и невыпуклыми. Выпуклый Вогнутый
Многогранники в стереометрии. Стереометрия-раздел геометрии, в котором изучаются свойства фигур в пространстве (пространственных фигур). Слово «стереометрия» состоит из греческих слов «стереос» – телесный, пространственный и «метрео» измеряю. Многогранники могут быть выпуклыми и невыпуклыми. Выпуклый Вогнутый
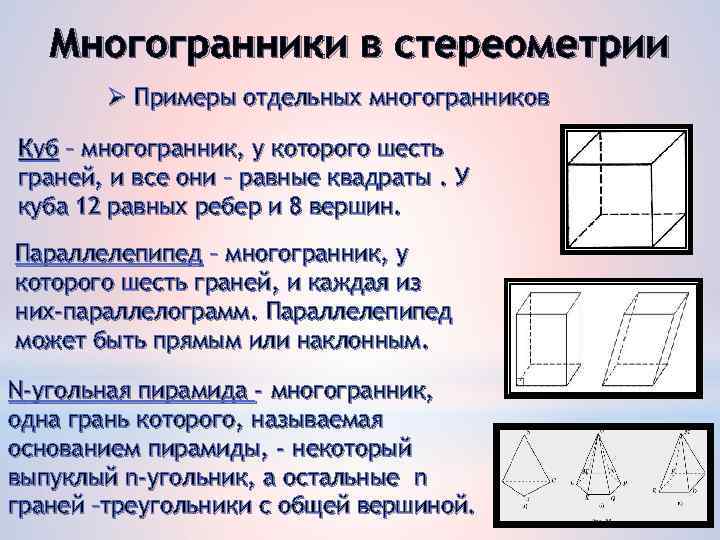 Многогранники в стереометрии Ø Примеры отдельных многогранников Куб – многогранник, у которого шесть граней, и все они – равные квадраты. У куба 12 равных ребер и 8 вершин. Параллелепипед – многогранник, у которого шесть граней, и каждая из них-параллелограмм. Параллелепипед может быть прямым или наклонным. N-угольная пирамида - многогранник, одна грань которого, называемая основанием пирамиды, - некоторый выпуклый n-угольник, а остальные n граней –треугольники с общей вершиной.
Многогранники в стереометрии Ø Примеры отдельных многогранников Куб – многогранник, у которого шесть граней, и все они – равные квадраты. У куба 12 равных ребер и 8 вершин. Параллелепипед – многогранник, у которого шесть граней, и каждая из них-параллелограмм. Параллелепипед может быть прямым или наклонным. N-угольная пирамида - многогранник, одна грань которого, называемая основанием пирамиды, - некоторый выпуклый n-угольник, а остальные n граней –треугольники с общей вершиной.
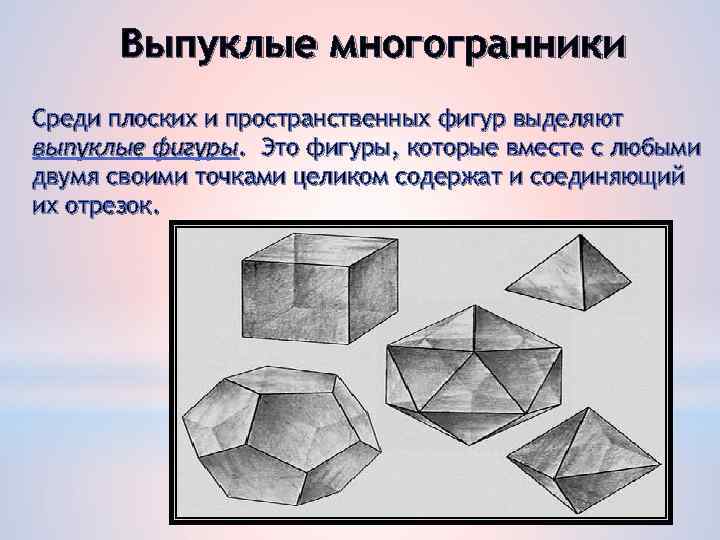 Выпуклые многогранники Среди плоских и пространственных фигур выделяют выпуклые фигуры. Это фигуры, которые вместе с любыми двумя своими точками целиком содержат и соединяющий их отрезок.
Выпуклые многогранники Среди плоских и пространственных фигур выделяют выпуклые фигуры. Это фигуры, которые вместе с любыми двумя своими точками целиком содержат и соединяющий их отрезок.
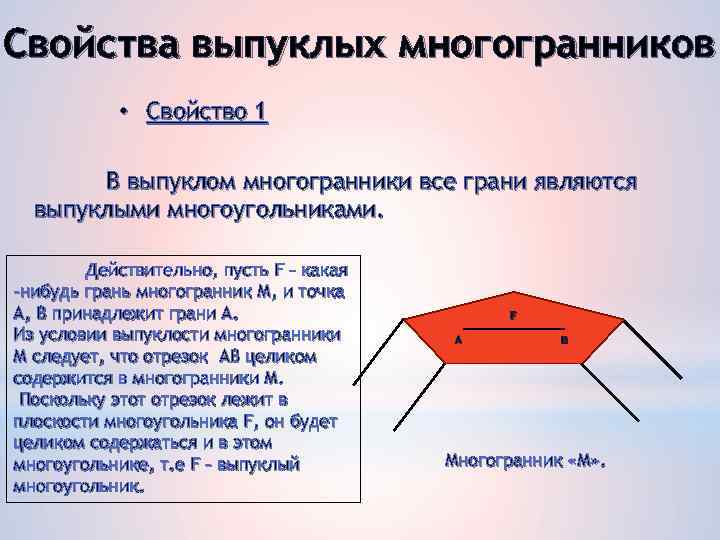 Свойства выпуклых многогранников • Свойство 1 В выпуклом многогранники все грани являются выпуклыми многоугольниками. Действительно, пусть F – какая -нибудь грань многогранник М, и точка А, В принадлежит грани А. Из условии выпуклости многогранники М следует, что отрезок АВ целиком содержится в многогранники М. Поскольку этот отрезок лежит в плоскости многоугольника F, он будет целиком содержаться и в этом многоугольнике, т. е F – выпуклый многоугольник. F А В Многогранник «М» .
Свойства выпуклых многогранников • Свойство 1 В выпуклом многогранники все грани являются выпуклыми многоугольниками. Действительно, пусть F – какая -нибудь грань многогранник М, и точка А, В принадлежит грани А. Из условии выпуклости многогранники М следует, что отрезок АВ целиком содержится в многогранники М. Поскольку этот отрезок лежит в плоскости многоугольника F, он будет целиком содержаться и в этом многоугольнике, т. е F – выпуклый многоугольник. F А В Многогранник «М» .
 Свойства выпуклых многогранников • Свойство 2 Всякий выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника. Пусть М –выпуклый многогранник. Возьмем какую-нибудь внутреннюю точку S многогранника М, т. е такую его точку, которая не принадлежит ни одной грани многогранника М. Соединим точку S с вершинами многогранника М отрезками. Заметим, что в силу выпуклости многогранника М все эти отрезки содержится в М. Рассмотрим пирамиды с вершиной S, основаниями которых являются грани многогранника М. Эти пирамиды целиком содержатся в М и все вместе составляют многогранник M.
Свойства выпуклых многогранников • Свойство 2 Всякий выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника. Пусть М –выпуклый многогранник. Возьмем какую-нибудь внутреннюю точку S многогранника М, т. е такую его точку, которая не принадлежит ни одной грани многогранника М. Соединим точку S с вершинами многогранника М отрезками. Заметим, что в силу выпуклости многогранника М все эти отрезки содержится в М. Рассмотрим пирамиды с вершиной S, основаниями которых являются грани многогранника М. Эти пирамиды целиком содержатся в М и все вместе составляют многогранник M.
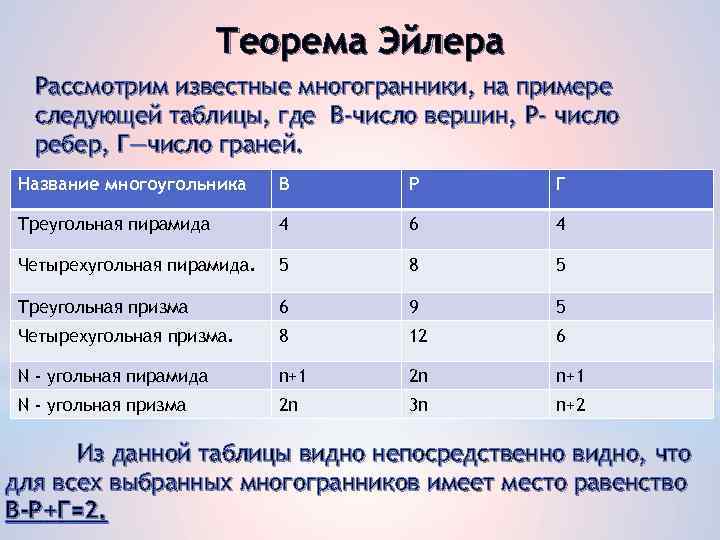 Теорема Эйлера Рассмотрим известные многогранники, на примере следующей таблицы, где В-число вершин, P- число ребер, Г—число граней. Название многоугольника B P Г Треугольная пирамида 4 6 4 Четырехугольная пирамида. 5 8 5 Треугольная призма 6 9 5 Четырехугольная призма. 8 12 6 N - угольная пирамида n+1 2 n n+1 N - угольная призма 2 n 3 n n+2 Из данной таблицы видно непосредственно видно, что для всех выбранных многогранников имеет место равенство В-Р+Г=2.
Теорема Эйлера Рассмотрим известные многогранники, на примере следующей таблицы, где В-число вершин, P- число ребер, Г—число граней. Название многоугольника B P Г Треугольная пирамида 4 6 4 Четырехугольная пирамида. 5 8 5 Треугольная призма 6 9 5 Четырехугольная призма. 8 12 6 N - угольная пирамида n+1 2 n n+1 N - угольная призма 2 n 3 n n+2 Из данной таблицы видно непосредственно видно, что для всех выбранных многогранников имеет место равенство В-Р+Г=2.
 Теорема Эйлера
Теорема Эйлера
 Полуправильные многогранники Убедившись в том, что нельзя построить шестой правильный многогранник, Архимед стал строить многогранники, гранями которых являются правильные, но не одноименные многоугольники, а в каждой вершине, как и у правильных многогранников , сходится одно и то же число рёбер. Так он получил 13 равноугольных полуправильных многоугольников.
Полуправильные многогранники Убедившись в том, что нельзя построить шестой правильный многогранник, Архимед стал строить многогранники, гранями которых являются правильные, но не одноименные многоугольники, а в каждой вершине, как и у правильных многогранников , сходится одно и то же число рёбер. Так он получил 13 равноугольных полуправильных многоугольников.
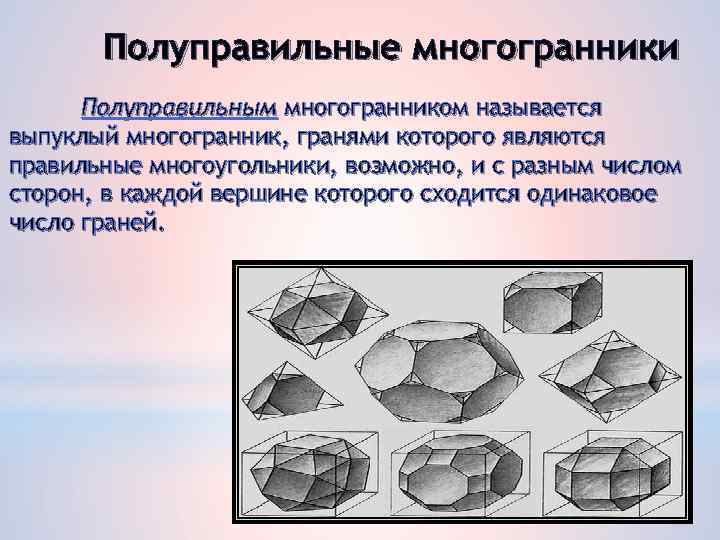 Полуправильные многогранники Полуправильным многогранником называется выпуклый многогранник, гранями которого являются правильные многоугольники, возможно, и с разным числом сторон, в каждой вершине которого сходится одинаковое число граней.
Полуправильные многогранники Полуправильным многогранником называется выпуклый многогранник, гранями которого являются правильные многоугольники, возможно, и с разным числом сторон, в каждой вершине которого сходится одинаковое число граней.
 Усеченный тетраэдр Если срезать углы тетраэдра плоскостями, каждая из которых отсекает третью часть его рёбер, выходящих из одной вершины, то получим усеченный тетраэдр, имеющий восемь граней.
Усеченный тетраэдр Если срезать углы тетраэдра плоскостями, каждая из которых отсекает третью часть его рёбер, выходящих из одной вершины, то получим усеченный тетраэдр, имеющий восемь граней.
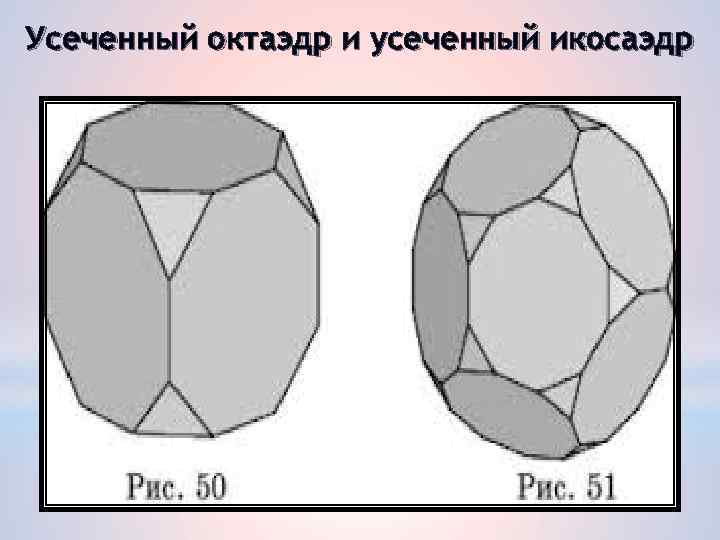 Усеченный октаэдр и усеченный икосаэдр
Усеченный октаэдр и усеченный икосаэдр
 Кубооктаэдр Если провести в кубе отсекающие плоскости через середины ребер, выходящих из одной вершины, то мы получим полуправильный многогранник , который называется кубооктаэдром
Кубооктаэдр Если провести в кубе отсекающие плоскости через середины ребер, выходящих из одной вершины, то мы получим полуправильный многогранник , который называется кубооктаэдром
 Икосододекаэдр Если в додекаэдре отсекающие плоскости провести через середины ребер , выходящих из одной вершины, то получим многогранник, который называется икосододекаэдром.
Икосододекаэдр Если в додекаэдре отсекающие плоскости провести через середины ребер , выходящих из одной вершины, то получим многогранник, который называется икосододекаэдром.
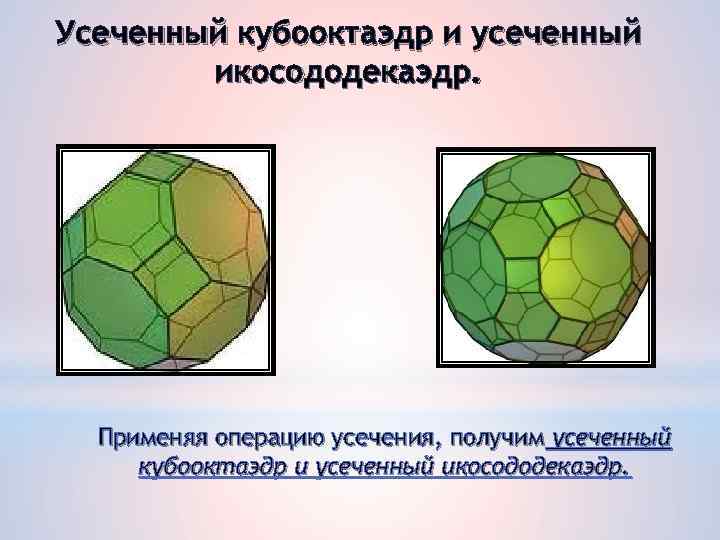 Усеченный кубооктаэдр и усеченный икосододекаэдр. Применяя операцию усечения, получим усеченный кубооктаэдр и усеченный икосододекаэдр.
Усеченный кубооктаэдр и усеченный икосододекаэдр. Применяя операцию усечения, получим усеченный кубооктаэдр и усеченный икосододекаэдр.
 Псевдоархимедовый многогранник Если повернуть верхнюю восьмиугольную чашу ромбокубооктаэдра многогранника на 45 градусов, то получится новый многогранник, который называется псевдоархимедовым.
Псевдоархимедовый многогранник Если повернуть верхнюю восьмиугольную чашу ромбокубооктаэдра многогранника на 45 градусов, то получится новый многогранник, который называется псевдоархимедовым.
 Ромбоикосододекаэдр – состоит из граней икосаэдра, додекаэдра и еще 30 квадратов.
Ромбоикосододекаэдр – состоит из граней икосаэдра, додекаэдра и еще 30 квадратов.
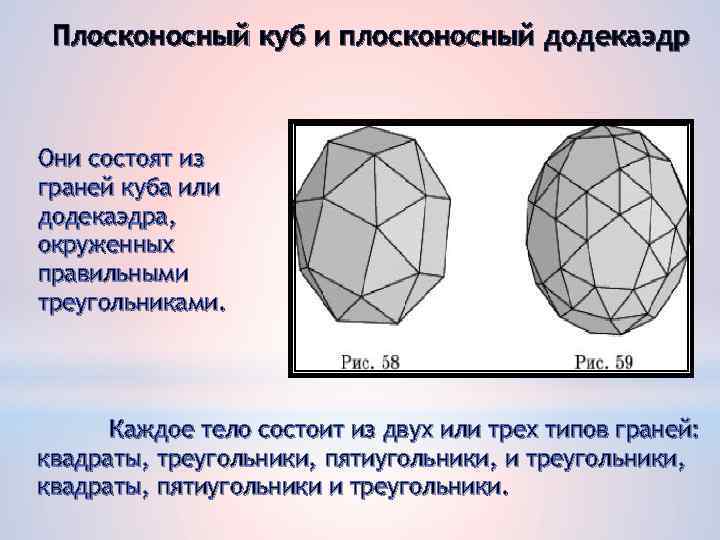 Плосконосный куб и плосконосный додекаэдр Они состоят из граней куба или додекаэдра, окруженных правильными треугольниками. Каждое тело состоит из двух или трех типов граней: квадраты, треугольники, пятиугольники, и треугольники, квадраты, пятиугольники и треугольники.
Плосконосный куб и плосконосный додекаэдр Они состоят из граней куба или додекаэдра, окруженных правильными треугольниками. Каждое тело состоит из двух или трех типов граней: квадраты, треугольники, пятиугольники, и треугольники, квадраты, пятиугольники и треугольники.
 Звездчатые многогранники Правильные звездчатые многогранники получаются из правильных многогранников продолжение граней или ребер Первые два правильных звездчатых многогранника были открыты И. Кеплером( 1571 -1630), а два других почти 200 лет спет построил французский математик и механик Л. Пуансо( 1777 -1859) И. Кеплер Л. Пуансо
Звездчатые многогранники Правильные звездчатые многогранники получаются из правильных многогранников продолжение граней или ребер Первые два правильных звездчатых многогранника были открыты И. Кеплером( 1571 -1630), а два других почти 200 лет спет построил французский математик и механик Л. Пуансо( 1777 -1859) И. Кеплер Л. Пуансо
 Звездчатые многогранники Если рассматривать правильные пятиугольники, то получится большой додекаэдр Если продолжит рёбра додекаэдра, то это приведет к замене каждой грани звездчатым правильным пятиугольником, и в результате возникает малый звездчатый додекаэдр.
Звездчатые многогранники Если рассматривать правильные пятиугольники, то получится большой додекаэдр Если продолжит рёбра додекаэдра, то это приведет к замене каждой грани звездчатым правильным пятиугольником, и в результате возникает малый звездчатый додекаэдр.
 Звездчатые многогранники Если в качестве граней рассматривать звездчатые пятиугольники, то получается большой звездчатый додекаэдр.
Звездчатые многогранники Если в качестве граней рассматривать звездчатые пятиугольники, то получается большой звездчатый додекаэдр.
 Звездчатые многогранники Икосаэдр имеет одну звездчатую форму. При продолжении граней правильного икосаэдра получается большой икосаэдр.
Звездчатые многогранники Икосаэдр имеет одну звездчатую форму. При продолжении граней правильного икосаэдра получается большой икосаэдр.
 Звездчатые многогранники в природе.
Звездчатые многогранники в природе.


