Тема Метрические задачи Цель ознакомиться и научиться решать

Тема: Метрические задачи Цель: ознакомиться и научиться решать различные типы метрических задач Задачи: 1. Понятие метрических задач 2. Определение натуральной величины А) Метод прямоугольного треугольника б) Метод вращения и совмещения в) Метод замены плоскостей проекции 3. Построение касательной и нормали к плоскости и поверхности 4. Построение разверток

Метрические задачи Метрическими называются задачи, в которых необходимо определить значения геометрических величин – длин отрезков, размеры углов расстояние между геометрическими фигурами, площади, объемы, а также задачи на построение геометрических фигур по заданным метрическим характеристикам.

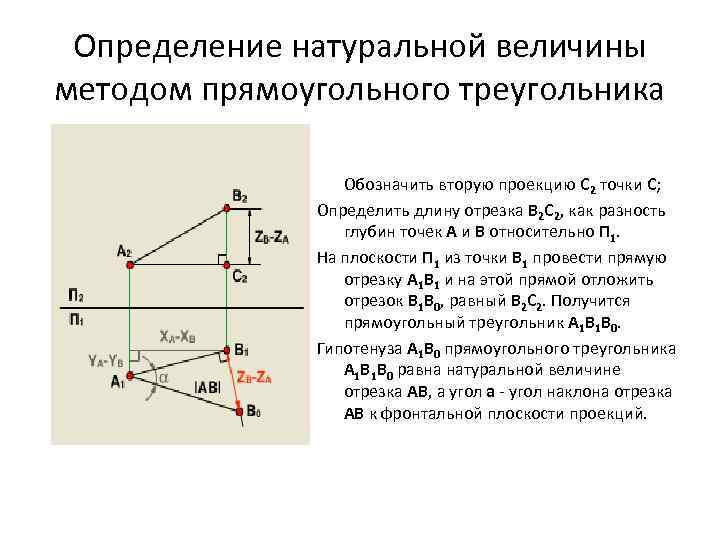Определение натуральной величины методом прямоугольного треугольника Обозначить вторую проекцию С 2 точки С; Определить длину отрезка В 2 С 2, как разность глубин точек А и В относительно П 1. На плоскости П 1 из точки В 1 провести прямую отрезку А 1 В 1 и на этой прямой отложить отрезок В 1 B 0, равный В 2 С 2. Получится прямоугольный треугольник А 1 В 1 B 0. Гипотенуза А 1 B 0 прямоугольного треугольника А 1 В 1 B 0 равна натуральной величине отрезка АВ, а угол a - угол наклона отрезка АВ к фронтальной плоскости проекций.

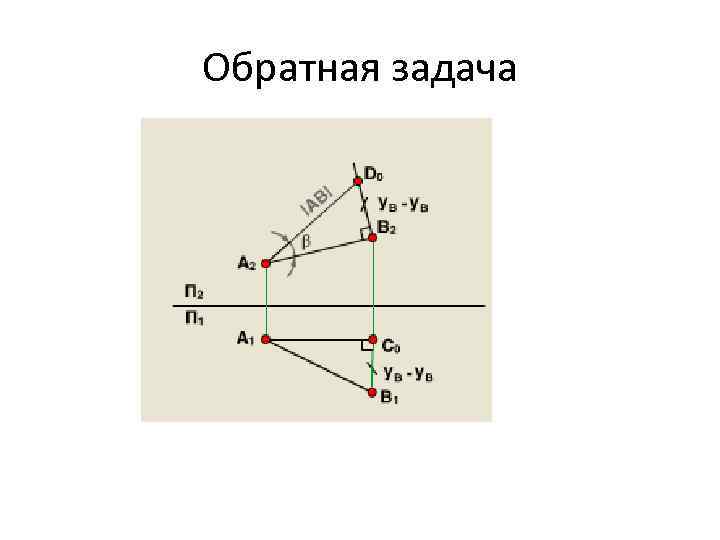Обратная задача

Способы нахождения натуральной величины геометрических образов Решение позиционных и метрических задач становится проще, если геометрические фигуры находятся в частном положении относительно плоскостей проекций. Для того, чтобы геометрические фигуры заняли частное положение, необходимо выполнить преобразование чертежа. Существует несколько способов преобразования ортогонального чертежа: • • • Способ замены плоскостей проекций; Способ дополнительного проецирования; Способ плоскопараллельного движения; Способ вращения вокруг проецирующей прямой; Способ вращения вокруг прямой уровня.

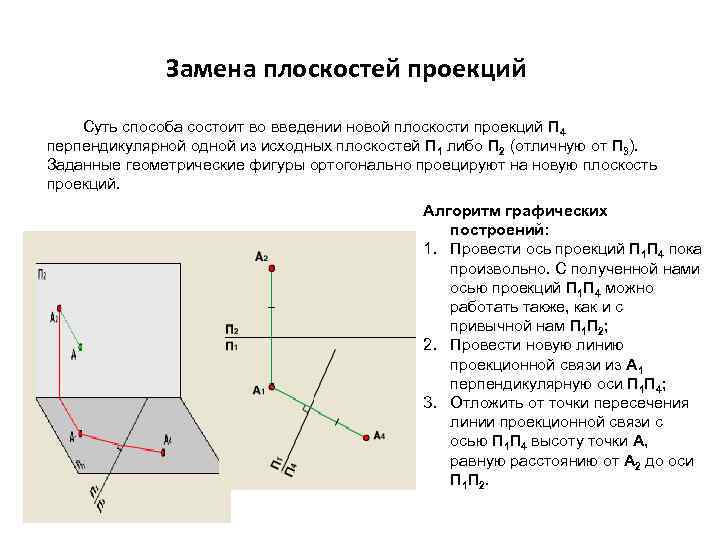Замена плоскостей проекций Суть способа состоит во введении новой плоскости проекций П 4 перпендикулярной одной из исходных плоскостей П 1 либо П 2 (отличную от П 3). Заданные геометрические фигуры ортогонально проецируют на новую плоскость проекций. Алгоритм графических построений: 1. Провести ось проекций П 1 П 4 пока произвольно. С полученной нами осью проекций П 1 П 4 можно работать также, как и с привычной нам П 1 П 2; 2. Провести новую линию проекционной связи из A 1 перпендикулярную оси П 1 П 4; 3. Отложить от точки пересечения линии проекционной связи с осью П 1 П 4 высоту точки A, равную расстоянию от A 2 до оси П 1 П 2.

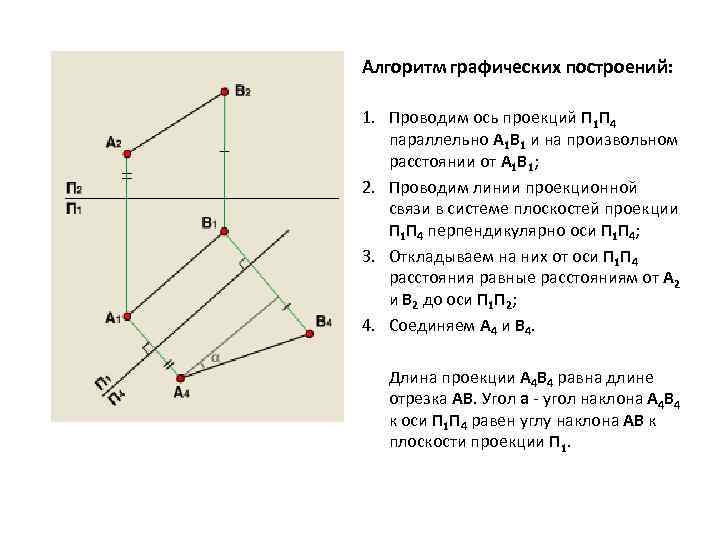Алгоритм графических построений: 1. Проводим ось проекций П 1 П 4 параллельно A 1 B 1 и на произвольном расстоянии от A 1 B 1; 2. Проводим линии проекционной связи в системе плоскостей проекции П 1 П 4 перпендикулярно оси П 1 П 4; 3. Откладываем на них от оси П 1 П 4 расстояния равные расстояниям от А 2 и B 2 до оси П 1 П 2; 4. Соединяем А 4 и B 4. Длина проекции А 4 B 4 равна длине отрезка АВ. Угол a - угол наклона А 4 B 4 к оси П 1 П 4 равен углу наклона АВ к плоскости проекции П 1.

Преобразование прямой общего положения в проецирующую прямую Алгоритм графических построений: 1. Проводим ось проекций П 1 П 4 параллельно A 1 B 1 и на произвольном расстоянии от A 1 B 1; 2. Проводим линии проекционной связи в системе плоскостей проекции П 1 П 4 перпендикулярно оси П 1 П 4; 3. Откладываем на них от оси П 1 П 4 расстояния равные расстояниям от А 2 и B 2 до оси П 1 П 2; 4. Соединяем А 4 и B 4; 5. Проводим ось проекций П 4 П 5 перпендикулярно A 4 B 4 и на произвольном расстоянии от A 4 B 4; 6. Проводим линию проекционной связи в системе плоскостей проекции П 4 П 5 перпендикулярно оси П 4 П 5; 7. Откладываем от оси П 4 П 5 расстояние равное расстоянию от отрезка А 1 B 1 до оси П 1 П 4; 8. Получаем проекцию отрезка AB на плоскость проекций П 5 в виде точки А 5 = B 5.

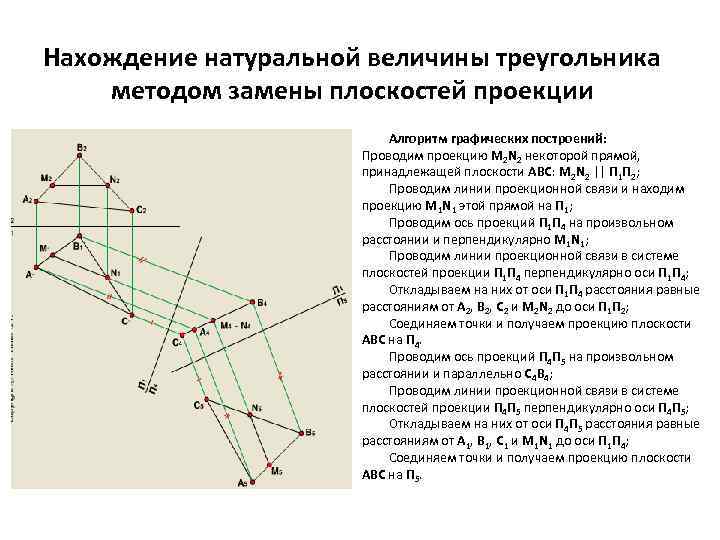Нахождение натуральной величины треугольника методом замены плоскостей проекции Алгоритм графических построений: Проводим проекцию M 2 N 2 некоторой прямой, принадлежащей плоскости АВС: M 2 N 2 || П 1 П 2; Проводим линии проекционной связи и находим проекцию M 1 N 1 этой прямой на П 1; Проводим ось проекций П 1 П 4 на произвольном расстоянии и перпендикулярно M 1 N 1; Проводим линии проекционной связи в системе плоскостей проекции П 1 П 4 перпендикулярно оси П 1 П 4; Откладываем на них от оси П 1 П 4 расстояния равные расстояниям от А 2, B 2, C 2 и M 2 N 2 до оси П 1 П 2; Соединяем точки и получаем проекцию плоскости ABC на П 4. Проводим ось проекций П 4 П 5 на произвольном расстоянии и параллельно C 4 B 4; Проводим линии проекционной связи в системе плоскостей проекции П 4 П 5 перпендикулярно оси П 4 П 5; Откладываем на них от оси П 4 П 5 расстояния равные расстояниям от А 1, B 1, C 1 и M 1 N 1 до оси П 1 П 4; Соединяем точки и получаем проекцию плоскости ABC на П 5.

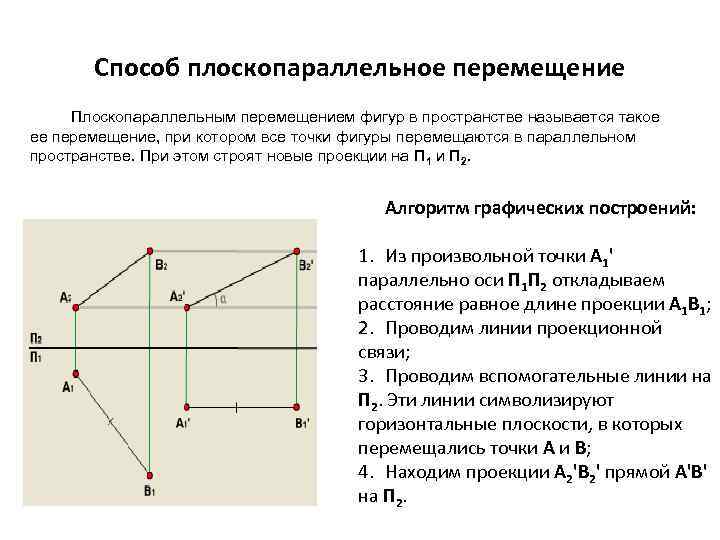Способ плоскопараллельное перемещение Плоскопараллельным перемещением фигур в пространстве называется такое ее перемещение, при котором все точки фигуры перемещаются в параллельном пространстве. При этом строят новые проекции на П 1 и П 2. Алгоритм графических построений: 1. Из произвольной точки A 1' параллельно оси П 1 П 2 откладываем расстояние равное длине проекции А 1 В 1; 2. Проводим линии проекционной связи; 3. Проводим вспомогательные линии на П 2. Эти линии символизируют горизонтальные плоскости, в которых перемещались точки A и B; 4. Находим проекции A 2'B 2' прямой A'B' на П 2.

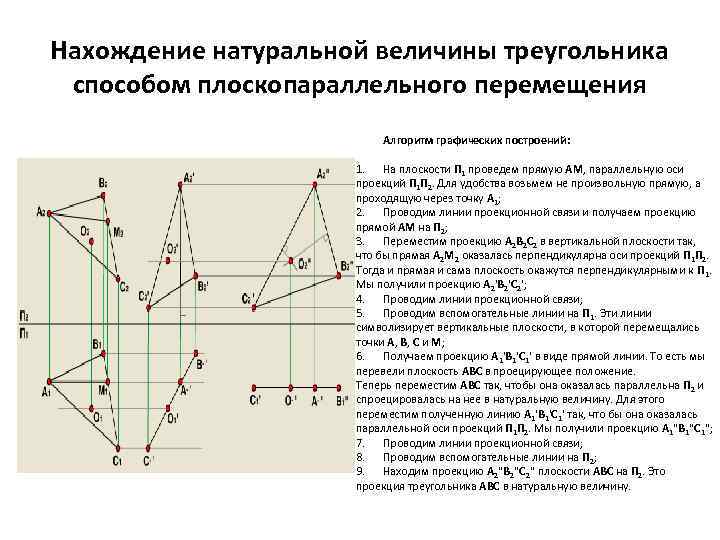Нахождение натуральной величины треугольника способом плоскопараллельного перемещения Алгоритм графических построений: 1. На плоскости П 1 проведем прямую AM, параллельную оси проекций П 1 П 2. Для удобства возьмем не произвольную прямую, а проходящую через точку A 1; 2. Проводим линии проекционной связи и получаем проекцию прямой AM на П 2; 3. Переместим проекцию A 2 B 2 C 2 в вертикальной плоскости так, что бы прямая A 2 M 2 оказалась перпендикулярна оси проекций П 1 П 2. Тогда и прямая и сама плоскость окажутся перпендикулярными к П 1. Мы получили проекцию A 2'B 2'C 2'; 4. Проводим линии проекционной связи; 5. Проводим вспомогательные линии на П 1. Эти линии символизирует вертикальные плоскости, в которой перемещались точки A, B, С и M; 6. Получаем проекцию A 1'B 1'C 1' в виде прямой линии. То есть мы перевели плоскость ABC в проецирующее положение. Теперь переместим ABC так, чтобы она оказалась параллельна П 2 и спроецировалась на нее в натуральную величину. Для этого переместим полученную линию A 1'B 1'C 1' так, что бы она оказалась параллельной оси проекций П 1 П 2. Мы получили проекцию A 1"B 1"C 1"; 7. Проводим линии проекционной связи; 8. Проводим вспомогательные линии на П 2; 9. Находим проекцию A 2"B 2"C 2" плоскости ABC на П 2. Это проекция треугольника ABC в натуральную величину.

Способ вращения вокруг проецирующей прямой Этот способ является частным случаем способа плоскопараллельного перемещения, когда точка фигуры описывает дугу окружности, плоскость которой также параллельна плоскости проекций. Графический алгоритм построения точек в способе вращения вокруг проецирующей прямой отличается лишь тем, что здесь траектория движения точки имеет вид окружности, а не произвольной прямой, как в плоскопараллельном проецировании. Алгоритм графических построений: 1. Проведем ось вращения i через точку B. Ось i перпендикулярна П 2; 2. Повернем отрезок AB до состояния параллельности оси проекций П 1 П 2. Где A 1'B 1' - новая проекция AB; 3. Проводим вспомогательную линию на П 2. Эта линия символизирует горизонтальную плоскость, в которой поворачивалась точка A; 4. Проводим линию связи и находим новую проекцию A 2'B 2' отрезка AB на П 2; 5. A 2'B 2' - натуральная величина отрезка AB.

Нахождение натуральной величины треугольника способом вращения вокруг проецирующей прямой Алгоритм графических построений: 1. Проводим первую ось вращения i; 2. В треугольнике АВС проводим горизонталь C 2 M 2 и находим ее проекцию на П 1; 3. Поворачиваем A 1 B 1 C 1 вокруг оси i до положения, при котором C 1 M 1 будет перпендикулярен оси проекций П 1 П 2; 4. A 1'B 1'C 1' - горизонтальная проекция после первого поворота; 5. Параллельно оси проекций проводим фронтальные проекции дуг, по которым двигаются точки А В С на П 2. На чертеже это вспомогательные линии серого цвета; 6. Из A 1'B 1'C 1' проводим линии проекционной связи до пересечения с соответствующими проекциями дуг. A 2'B 2'C 2' - новая фронтальная проекция АВС после первого поворота. a - искомый угол наклона плоскости АВС к П 1; 7. Проводим ось j через точку В'; 8. Поворачиваем A 2'B 2'C 2' до положения параллельного оси проекций. A 2"B 2"C 2" - фронтальная проекция АВС после второго поворота; 9. Параллельно оси проекций проводим горизонтальные проекции дуг, по которым двигаются точки А В С на П 1. На чертеже это вспомогательные линии серого цвета; 10. Из A 2"B 2"C 2" проводим линии проекционной связи до пересечения с соответствующими проекциями дуг. A 1"B 1"C 1" - новая горизонтальная проекция треугольника АВС в натуральную величину после второго поворота.

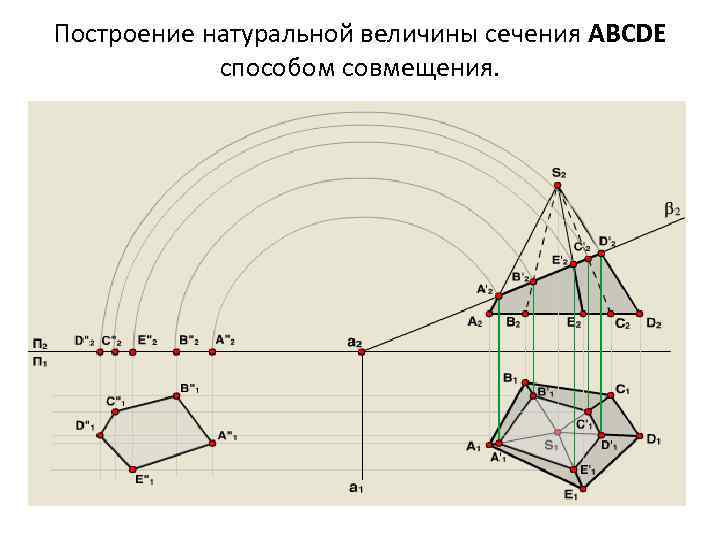Построение натуральной величины сечения ABCDE способом совмещения.

Признак перпендикулярности прямой и плоскости прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. Для задания прямой перпендикулярной плоскости в качестве пересекающихся прямых удобно выбрать линии уровня – фронталь и горизонталь. В этом случае можно воспользоваться свойствами проекций прямого угла. Теорема: Для того, чтобы прямая m была перпендикулярна плоскости s, необходимо и достаточно, чтобы горизонтальная проекция прямой m 1 была горизонтальной проекции горизонтали (m 1 h 1), а фронтальная проекция прямой m 2 – фронтальной проекции фронтали (m 2 f 2). Решение: 1. На ортогональном чертеже строим в плоскости s (ABC) проекции фронтали f (f 1, f 2) и горизонтали h (h 1, h 2). 2. Проводим m 1 h 1 причем D 1 m 1. 3. Проводим m 2 f 2 причем D 2 m 2. Прямая m (m 1, m 2) – искомый перпендикуляр, так как она перпендикулярна двум пересекающимся прямым плоскости s (ABC) = h f.

Касательная и нормаль к поверхности Касательной к поверхности в некоторой ее точке называют прямую, касательную к какой-либо кривой на поверхности, проходящей через данную точку. В данной точке М поверхности Θ можно провести бесчисленное множество касательных прямых ti. Множество касательных ti, проведенных к поверхности в некоторой ее точке М, принадлежит плоскости S, если точка М является регулярной точкой поверхности. Касательной плоскостью к поверхности ее в регулярной точке называют плоскость, содержащую множество касательных, проведенных к всевозможным кривым поверхности, проходящим через эту точку. Касательная плоскость S к поверхности Θ в точке М однозначно определяется двумя касательными t 11 и t 2, проведённым к кривым а и b поверхности Θ, проходящими через точку М. С понятием касательной плоскости тесно связано понятие нормали к поверхности. Нормалью n поверхности Θ в некоторой ее точке М называют прямую, проходящую через эту точку и перпендикулярную касательной плоскости, построенной в этой точке.

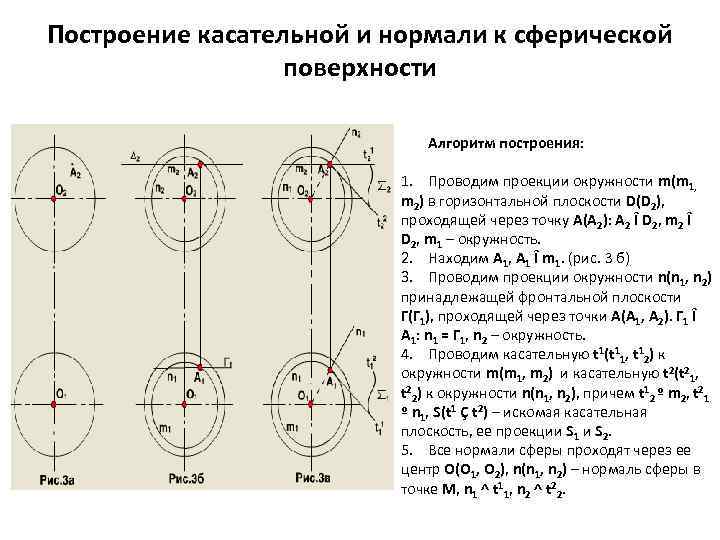Построение касательной и нормали к сферической поверхности Алгоритм построения: 1. Проводим проекции окружности m(m 1, m 2) в горизонтальной плоскости D(D 2), проходящей через точку А(А 2): А 2 Î D 2, m 1 – окружность. 2. Находим А 1, А 1 Î m 1. (рис. 3 б) 3. Проводим проекции окружности n(n 1, n 2) принадлежащей фронтальной плоскости Г(Г 1), проходящей через точки А(А 1, А 2). Г 1 Î А 1: n 1 = Г 1, n 2 – окружность. 4. Проводим касательную t 1(t 11, t 12) к окружности m(m 1, m 2) и касательную t 2(t 21, t 22) к окружности n(n 1, n 2), причем t 12 º m 2, t 21 º n 1, S(t 1 Ç t 2) – искомая касательная плоскость, ее проекции S 1 и S 2. 5. Все нормали сферы проходят через ее центр О(О 1, О 2), n(n 1, n 2) – нормаль сферы в точке М, n 1 ^ t 11, n 2 ^ t 22.

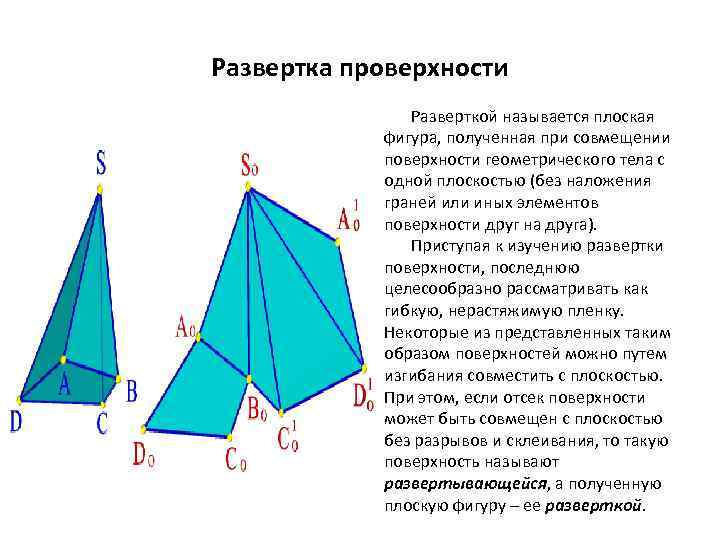Развертка проверхности Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга). Приступая к изучению развертки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру – ее разверткой.

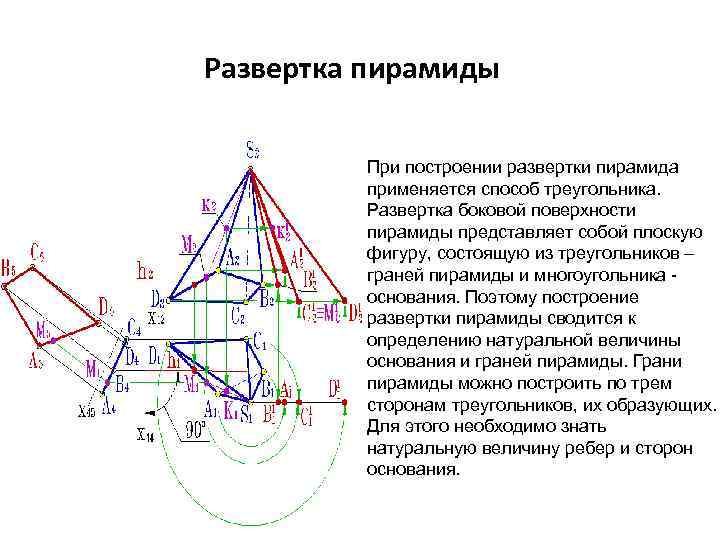Развертка пирамиды При построении развертки пирамида применяется способ треугольника. Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников – граней пирамиды и многоугольника - основания. Поэтому построение развертки пирамиды сводится к определению натуральной величины основания и граней пирамиды. Грани пирамиды можно построить по трем сторонам треугольников, их образующих. Для этого необходимо знать натуральную величину ребер и сторон основания.

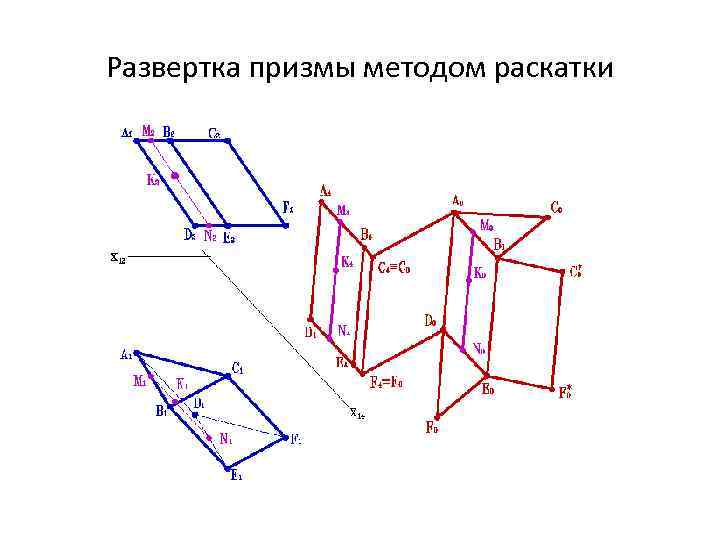Развертка призмы методом раскатки

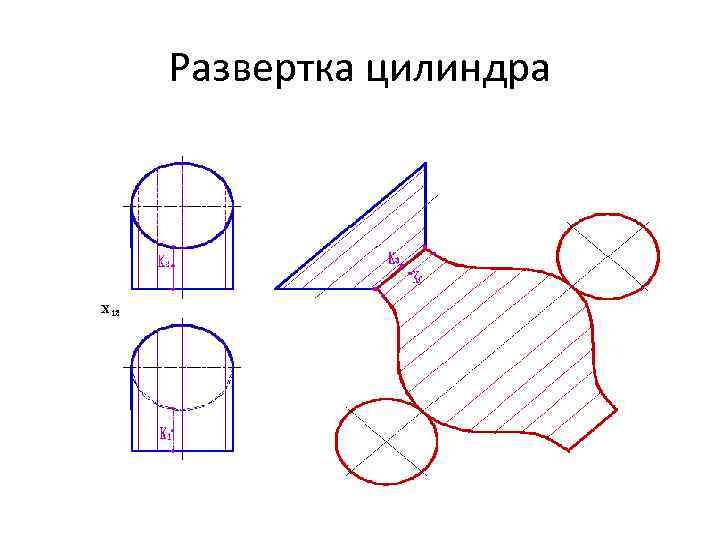Развертка цилиндра

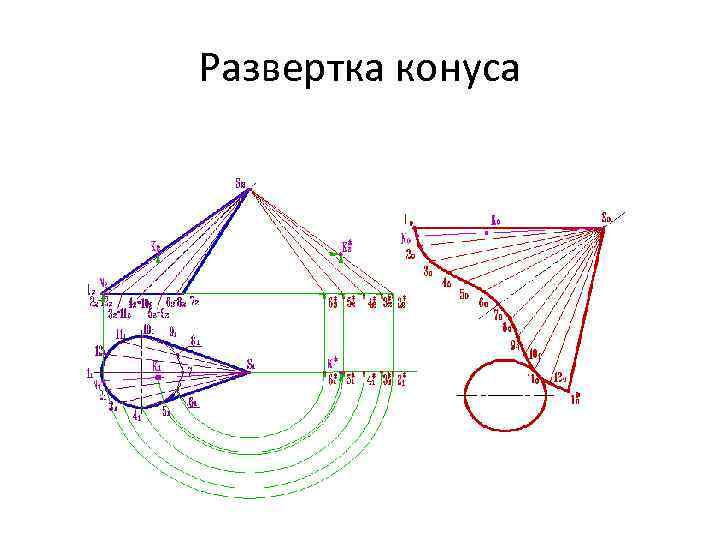Развертка конуса

Домашнее задание Перечислить развертывающиеся и не развертывающиеся поверхности подготовится к текущему тестированию