Л6 Выборочный метод.pptx
- Количество слайдов: 29

Тема МЕТОД ВЫБОРОЧНЫХ НАБЛЮДЕНИЙ План 1. Понятие о выборочном наблюдении и ошибках репрезентативности. 2. Способ формирования выборочных совокупностей. 3. Ошибки выборки. Средняя и предельная ошибка выборки. 4. Определение необходимого объёма выборки

1. Понятие о выборочном наблюдении и ошибках репрезентативности. Наблюдения бывают сплошные и несплошные. . При сплошном обследуются все единицы совокупности, а при несплошном только некоторая часть этих единиц. Эта часть должна быть достаточно массовой, т. к. на её основе строятся статистические показатели, которые затем становятся показателями всей совокупности. Основной вид несплошных – выборочное наблюдение Выборочный метод – это научно-обоснованное и спланированное наблюдение статистической совокупности, необходимое для получения статистических оценок всей совокупности в целом на основе оценок части этой совокупности.

Преимущества метода заключаются в существенной экономии значительного вида следующих ресурсов: § финансовых средств, затрачиваемых на сбор и обработку данных, подготовку и оплату кадров; § материально-технических ресурсов (канцтовары, оргтехника, транспорт); § трудовых ресурсов, привлекаемых к обследованию на всех его этапах; § времени, затраченного как на получение первичной информации, так и на последующую ее обработку.

Реализация выборочного метода базируется на понятиях генеральной и выборочной совокупностей. Совокупность, из которой производится отбор, называется генеральной, а все её показатели – генеральными показателями. Совокупность единиц, отобранных по определённым правилам из генеральной совокупности, называется выборочной совокупностью или выборкой, а показатели – выборочными. Отбор единиц в выборку всегда случаен, значит и выборка случайна. Тогда статистические характеристики выборки также случайны, поэтому они могут отклоняться от истинных характеристик генеральной совокупности. Следовательно, значения выборочных показателей являются только лишь приближёнными оценками генеральных показателей.
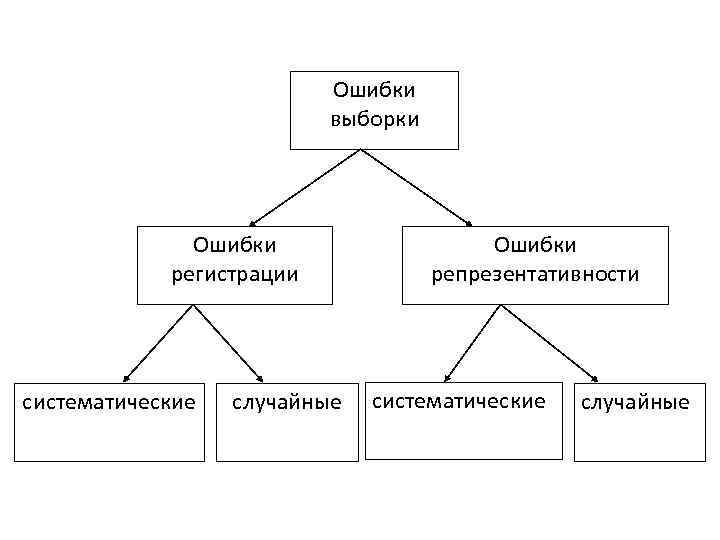
Ошибки выборки Ошибки регистрации систематические случайные Ошибки репрезентативности систематические случайные
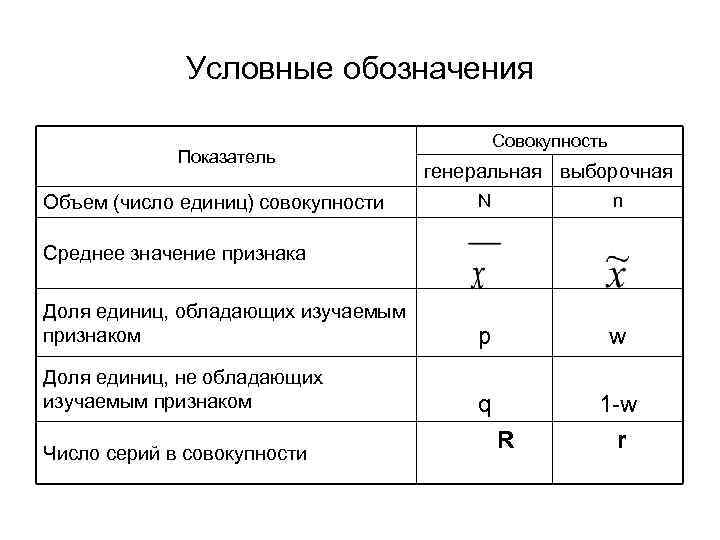
Условные обозначения Показатель Совокупность генеральная выборочная N n Доля единиц, обладающих изучаемым признаком p w Доля единиц, не обладающих изучаемым признаком q 1 -w r Объем (число единиц) совокупности Среднее значение признака Число серий в совокупности R

2. Способ формирования выборных совокупностей К наиболее распространенным на практике видам выборки относятся: • собственно – случайная (простая случайная) выборка; • механическая (систематическая) выборка; • типическая (стратифицированная, расслоенная) выборка; • серийная (гнездовая) выборка.
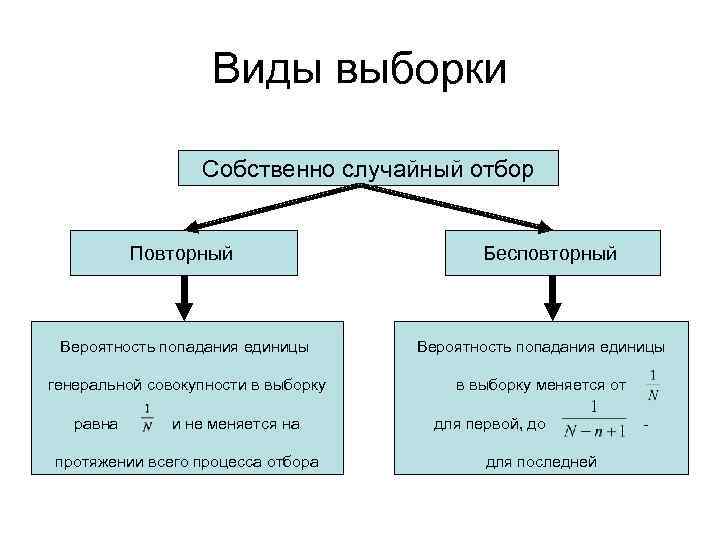
Виды выборки Собственно случайный отбор Собственно-случайный отбор Повторный Бесповторный Вероятность попадания единицы генеральной совокупности в выборку меняется от равна и не меняется на протяжении всего процесса отбора для первой, до для последней -

3. Ошибки выборки. Средняя и предельная ошибки выборки. Применение выборочного метода всегда связанно с измерениями степени достоверности оценок генеральных показателей, полученных на основе выборочных показателей. Достоверность этих оценок зависят от репрезентативности выборки, т. е. от того, насколько полно и правильно предоставлены в выборки статистические свойства генеральной совокупности. Как правило, генеральные и выборочные показатели не совпадают, а отклоняются на некоторую величину ε, которую называют ошибкой выборки или ошибкой репрезентативности.

Параметры выборочной совокупности случайны, следовательно, ошибки выборки также случайны, т. е. различные для различных выборок из одной и той же совокупности. Поэтому принято вычислять среднюю ошибку выборки и предельную. Средняя ошибка выборки – это среднее квадратическое отклонение выборочных средних относительно генеральной средней: где: – выборочная средняя для i-ой выборки; k – число всех возможных выборок данного объема генеральной совокупности.

Величина ошибки зависит от объёма выборки n и от степени вариации значения признаков, а именно, чем больше n и чем меньше вариация значений признака Х, тем меньше средняя ошибка выборки. Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от вида выборки и способа отбора единиц из генеральной совокупности. Предельная ошибка выборки определяет границы, в пределах которых будут находиться характеристики генеральной совокупности. Эти границы задают, так называемый, доверительный интервал генерального показателя. Это случайная область значений, которая с вероятностью Р гарантированно содержит значение генерального показателя. Эту вероятность Р называют доверительной вероятностью или уровнем надёжности. Чаще используют Р= 0. 954, Р= 0. 997, реже Р= 0, 683

В математической статистике доказано, что предельная ошибка выборки Δ кратна средней ошибке µ с коэффициентом кратности t, который зависит от значения доверительной вероятности Р, т. е. для предельной ошибки выборочной средней имеем: Соответствие между коэффициентом t: уровнем Вероятность, Pi 0, 683 0, 866 0, 954 Значение t 1, 0 1, 5 2, 0 надежности Р 0, 988 0, 997 0, 999 2, 5 3, 0 и 3, 5 Например, при t = 2 и Р = 0, 954 можно утверждать, что расхождение выборочной и генеральной средней не превысит двукратной величины средней ошибки.

Предельная ошибка выборки Δх позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы. Для генеральной средней: Для расчётов средних ошибок выборки существуют специальные формулы, которые зависят от вида выборки и способа отбора единиц из генеральной совокупности.

Формулы средней ошибки при собственослучайной и механической выборке Оцениваемый параметр Средняя Доля Повторный отбор Бесповторный отбор
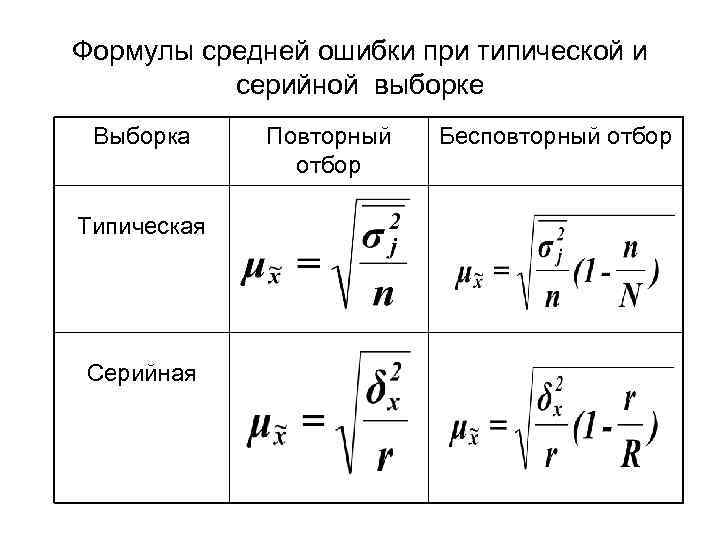
Формулы средней ошибки при типической и серийной выборке Выборка Типическая Серийная Повторный отбор Бесповторный отбор

Пример 1. Для определения среднего срока пользования кредитом в банке была проведена 5% механическая выборка, в которую попали 100 счетов. В результате установлено что, средний срок пользования кредитом составляет 30 дней при среднем квадратическом отклонении в 9 дней. В 10 -ти счетах из 100 срок пользования кредитом превышал 60 дней. Требуется с вероятностью p=0, 954 определить пределы, в которых будут находиться: 1)средний срок пользования кредитом в генеральной совокупности; 2)долю счетов в генеральной совокупности со сроком пользования кредитом более 60 дней. n = 100; N =(100/5)*100=2000; σ = 9; =30

1)средний срок пользования краткосрочным кредитом в генеральной совокупности будет находиться в пределах: Выборка механическая, тогда формулы расчёта для ошибок такие же, как для собственно случайной: 2)Доля краткосрочных кредитов со сроком пользования больше 60 дней в генеральной совокупности будет находиться в пределах:

m=10, n=100

4. Определение необходимого объема выборки При планировании выборочного обследования необходимо знать, каков должен быть объём выборки для того, чтобы обеспечить определённую точность расчётов генеральных параметров, т. е. средней величины и доли. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении, исходя из вероятности, на основе которой можно гарантировать величину устанавливаемой ошибки и на базе способа отбора. Формулы необходимого объема выборки могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки

Для собственно-случайной и механической выборок при повторном отборе из формул: и имеем откуда Для собственно-случайной и механической выборок при бесповторном отборе Пример 2. В районе проживает 2000 семей. Надо провести выборочное обследование методом бесповторного отбора для определения среднего состава семьи. Необходимо определить нужную численность выборки для заданного уровня надёжности Р=0, 954, чтобы ошибка выборки не превышает 1 чел. , при среднем квадратном отклонении 3 чел.

t = 2, σ= 3, N=2000, Δх = 1 Для типической выборки при повторном отборе имеем: Для типической выборки при бесповторном отборе: Пример 3. Проведена 10% бесповторная типическая выборка рабочих предприятия, пропорциональная размерам цехов, по потерям рабочего времени из-за временной нетрудоспособности. Необходимо с вероятностью 0, 954 оценить потери рабочего времени изза временной нетрудоспособности на одного рабочего по предприятию в целом.
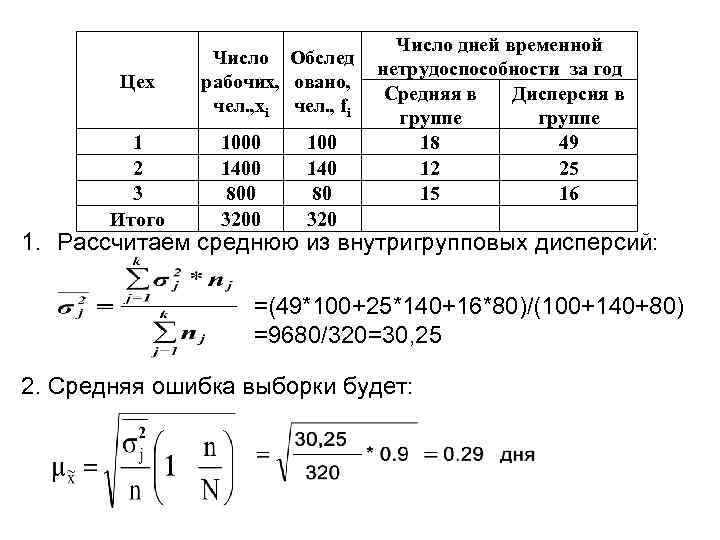
Цех 1 2 3 Итого Число Обслед рабочих, овано, чел. , xi чел. , fi 1000 1400 800 3200 140 80 320 Число дней временной нетрудоспособности за год Средняя в Дисперсия в группе 18 49 12 25 15 16 1. Рассчитаем среднюю из внутригрупповых дисперсий: =(49*100+25*140+16*80)/(100+140+80) =9680/320=30, 25 2. Средняя ошибка выборки будет:

3. Предельная ошибка выборки (t=2): Δ=2*0, 29=0, 58 дня 4. Выборочная средняя = (18*100+12*140+15*80)/(100+140+80)=4680/320 =14, 6 дня 5. Генеральная средняя 14, 6 -0, 58≤ ≤ 14, 6+0, 58 14, 02 дня≤ ≤ 15, 16 дня Вывод: С вероятностью 0, 954 можно утверждать, что среднее число временной нетрудоспособности одного рабочего в целом по предприятию находится в пределах от 14, 02 дней до 15, 16 дней.
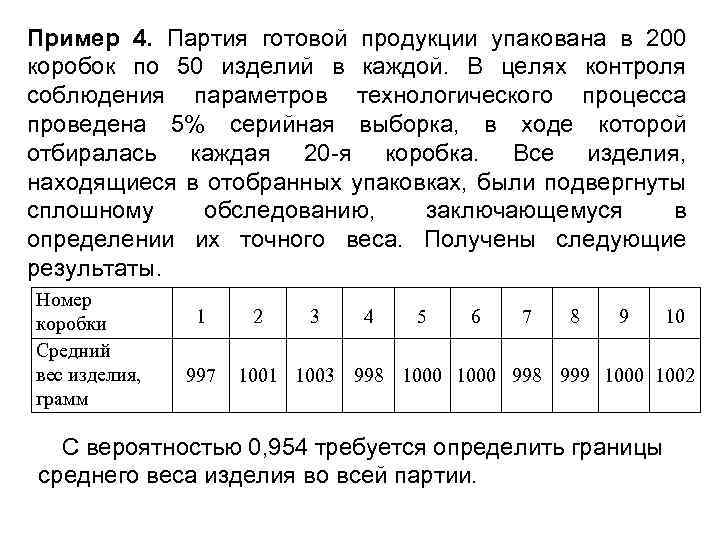
Пример 4. Партия готовой продукции упакована в 200 коробок по 50 изделий в каждой. В целях контроля соблюдения параметров технологического процесса проведена 5% серийная выборка, в ходе которой отбиралась каждая 20 -я коробка. Все изделия, находящиеся в отобранных упаковках, были подвергнуты сплошному обследованию, заключающемуся в определении их точного веса. Получены следующие результаты. Номер коробки Средний вес изделия, грамм 1 997 2 3 4 5 6 7 8 9 10 1001 1003 998 1000 998 999 1000 1002 С вероятностью 0, 954 требуется определить границы среднего веса изделия во всей партии.

1. Определим средний вес изделия по выборочной совокупности: =(997+1001+1003+…+1002)/10=999, 8 г 2. Рассчитаем межгрупповую дисперсию: 3. Средняя ошибка выборки: 4. Предельная ошибка: =2*0, 55=1, 1 г 5. Границы генеральной средней: 999, 8 -1, 1 998, 7 г 999, 8+1, 1 1000, 9 г

Пример 5. С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается провести типическую выборку пропорционально численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников 12000 чел. , в том числе 7000 – мужчин и 5000 – женщин. Известно, что средняя из внутригрупповых дисперсий составляет 1600. Определить необходимый объем выборки при вероятности 0, 997 и ошибке 5 чел. 1. Общая численность: 2. Объем групп: n 1=(550)*7000/12000=319 мужчин n 2=(550)*5000/12000=231 женщин

Расчет необходимого объема выборки При повторном отборе При бесповторном отборе

Формулы для нахождения необходимой численности выборки при собственнослучайном и механическом отборе Оцениваемый параметр Средняя Доля Повторный отбор Бесповторный отбор

Расчет дисперсии в малой выборке т. к. обязательно учитывается соотношение:
Л6 Выборочный метод.pptx