Тема «Математические модели тепловых






















8 Математические модели.ppt
- Количество слайдов: 33
 Тема «Математические модели тепловых процессов в изделиях из стекла» Специализация «Стекло и керамические материалы»
Тема «Математические модели тепловых процессов в изделиях из стекла» Специализация «Стекло и керамические материалы»
 План лекции Л 1– 2 1. Несовершенство упрощенных (интегральных) методик расчета тепловых процессов 2. Математическая модель теплообмена в слое монолитного стекла • Уравнение энергии • Уравнение переноса излучения • Уравнение дивергенции • Краевые условия 3. Математическая модель теплообмена в слое спекающегося стекла • Уравнение энергии • Уравнение диффузии излучения • Уравнение дивергенции • Уравнение спекания • Уравнение кристаллизации • Модели теплопроводности • Краевые условия 4. Программное обеспечение для теплового моделирования конструкций из стекла 5. Примеры расчета
План лекции Л 1– 2 1. Несовершенство упрощенных (интегральных) методик расчета тепловых процессов 2. Математическая модель теплообмена в слое монолитного стекла • Уравнение энергии • Уравнение переноса излучения • Уравнение дивергенции • Краевые условия 3. Математическая модель теплообмена в слое спекающегося стекла • Уравнение энергии • Уравнение диффузии излучения • Уравнение дивергенции • Уравнение спекания • Уравнение кристаллизации • Модели теплопроводности • Краевые условия 4. Программное обеспечение для теплового моделирования конструкций из стекла 5. Примеры расчета
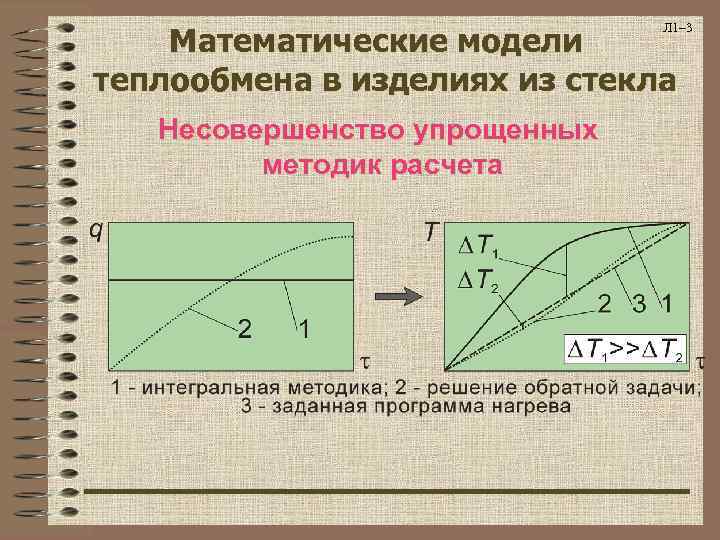
 Л 1– 3 Математические модели теплообмена в изделиях из стекла Несовершенство упрощенных методик расчета
Л 1– 3 Математические модели теплообмена в изделиях из стекла Несовершенство упрощенных методик расчета
 Л 1– 4 Математические модели теплообмена в изделиях из стекла СЛОЙ МОНОЛИТНОГО СТЕКЛА
Л 1– 4 Математические модели теплообмена в изделиях из стекла СЛОЙ МОНОЛИТНОГО СТЕКЛА
 Л 1– 5 Математическая модель радиационно- кондуктивного теплообмена в слое монолитного стекла
Л 1– 5 Математическая модель радиационно- кондуктивного теплообмена в слое монолитного стекла
 Л 1– 6 Математическая модель радиационно- кондуктивного теплообмена в слое монолитного стекла
Л 1– 6 Математическая модель радиационно- кондуктивного теплообмена в слое монолитного стекла
 Л 1– 7 Математическая модель радиационно- кондуктивного теплообмена в слое монолитного стекла
Л 1– 7 Математическая модель радиационно- кондуктивного теплообмена в слое монолитного стекла
 Л 1– 8 Математическая модель радиационно- кондуктивного теплообмена в слое монолитного стекла
Л 1– 8 Математическая модель радиационно- кондуктивного теплообмена в слое монолитного стекла
 Л 1– 9 Математические модели теплообмена в изделиях из стекла СПЕКАНИЕ СТЕКЛА
Л 1– 9 Математические модели теплообмена в изделиях из стекла СПЕКАНИЕ СТЕКЛА
 Л 1– 10 Математическая модель радиационно- кондуктивного теплообмена в слое спекающегося стекла
Л 1– 10 Математическая модель радиационно- кондуктивного теплообмена в слое спекающегося стекла
 Л 1– 11 Математическая модель радиационно- кондуктивного теплообмена в слое спекающегося стекла
Л 1– 11 Математическая модель радиационно- кондуктивного теплообмена в слое спекающегося стекла
 Л 1– 12 Математическая модель радиационно- кондуктивного теплообмена в слое спекающегося стекла
Л 1– 12 Математическая модель радиационно- кондуктивного теплообмена в слое спекающегося стекла
 Л 1– 13 Математическая модель радиационно- кондуктивного теплообмена в слое спекающегося стекла
Л 1– 13 Математическая модель радиационно- кондуктивного теплообмена в слое спекающегося стекла
 Л 1– 14 Математическая модель радиационно- кондуктивного теплообмена в слое спекающегося стекла
Л 1– 14 Математическая модель радиационно- кондуктивного теплообмена в слое спекающегося стекла
 Л 1– 15 Математическая модель радиационно- кондуктивного теплообмена в слое спекающегося стекла
Л 1– 15 Математическая модель радиационно- кондуктивного теплообмена в слое спекающегося стекла
 Л 1– 16 Методы решения 1. Метод конечных разностей 2. Метод итераций 3. Численное интегрирование по методу Гаусса 4. Многогрупповое приближение (для уравнения переноса излучения)
Л 1– 16 Методы решения 1. Метод конечных разностей 2. Метод итераций 3. Численное интегрирование по методу Гаусса 4. Многогрупповое приближение (для уравнения переноса излучения)
 Метод конечных разностей, • Постановка задачи: На для и аппроксимировать первую краевую задачу для линейного уравнения теплопроводности
Метод конечных разностей, • Постановка задачи: На для и аппроксимировать первую краевую задачу для линейного уравнения теплопроводности
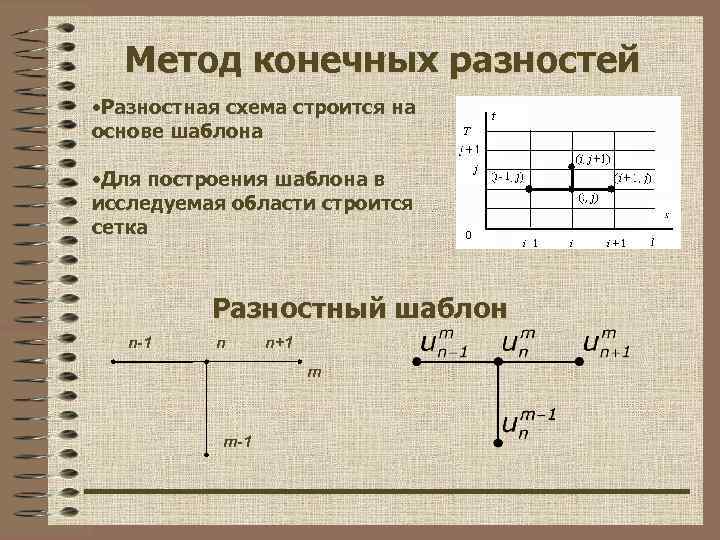
 Метод конечных разностей , • Разностная схема строится на основе шаблона • Для построения шаблона в исследуемая области строится сетка Разностный шаблон n-1 n n+1 m-1
Метод конечных разностей , • Разностная схема строится на основе шаблона • Для построения шаблона в исследуемая области строится сетка Разностный шаблон n-1 n n+1 m-1
 Метод конечных разностей , Составляется разностное уравнение на базе шаблона ; Если ввести обозначение , то разностную схему можно записать в виде
Метод конечных разностей , Составляется разностное уравнение на базе шаблона ; Если ввести обозначение , то разностную схему можно записать в виде
 Метод конечных разностей , и Организация расчета по разностной схеме : ; 1. Составленная разностная схема является неявной. Запишем уравнения для нахождения значений 2. Введем следующие обозначения
Метод конечных разностей , и Организация расчета по разностной схеме : ; 1. Составленная разностная схема является неявной. Запишем уравнения для нахождения значений 2. Введем следующие обозначения
 Метод конечных разностей , и Организация расчета по разностной схеме : ; 3. Получаем систему линейных уравнений 4. Полученную систему уравнений решаем методом прогонки
Метод конечных разностей , и Организация расчета по разностной схеме : ; 3. Получаем систему линейных уравнений 4. Полученную систему уравнений решаем методом прогонки
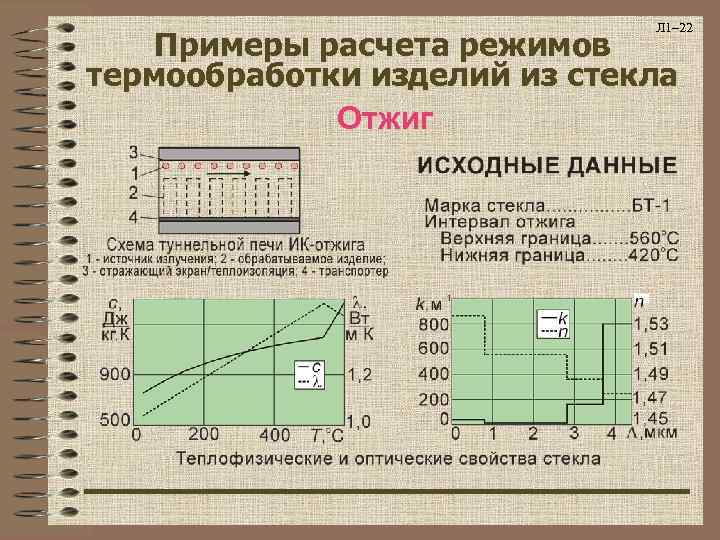
 Л 1– 22 Примеры расчета режимов термообработки изделий из стекла Отжиг
Л 1– 22 Примеры расчета режимов термообработки изделий из стекла Отжиг
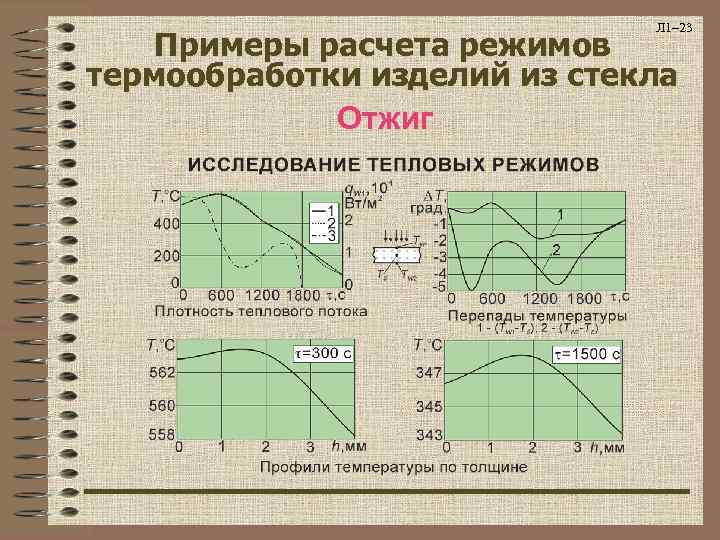
 Л 1– 23 Примеры расчета режимов термообработки изделий из стекла Отжиг
Л 1– 23 Примеры расчета режимов термообработки изделий из стекла Отжиг
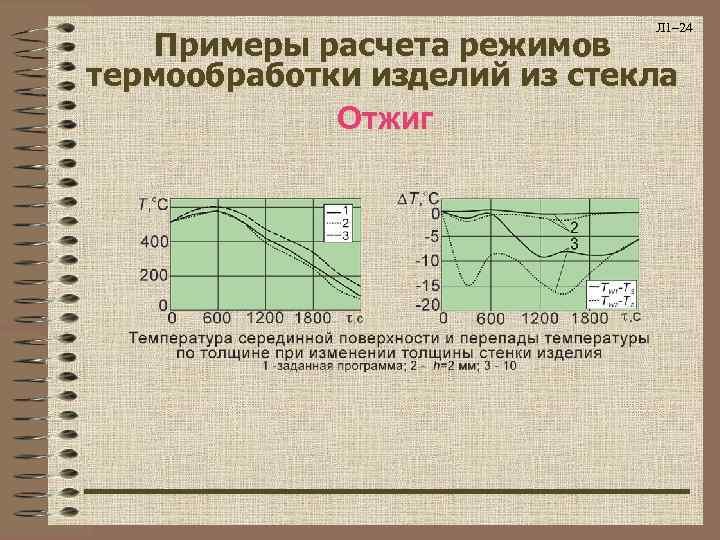
 Л 1– 24 Примеры расчета режимов термообработки изделий из стекла Отжиг
Л 1– 24 Примеры расчета режимов термообработки изделий из стекла Отжиг
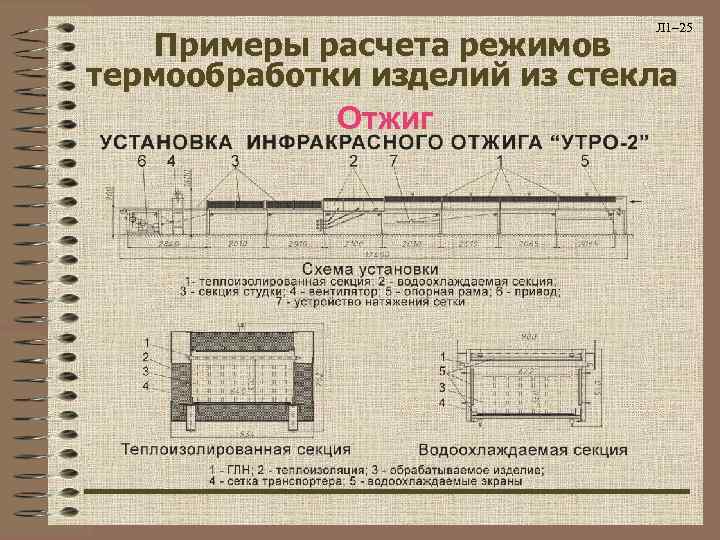
 Л 1– 25 Примеры расчета режимов термообработки изделий из стекла Отжиг
Л 1– 25 Примеры расчета режимов термообработки изделий из стекла Отжиг
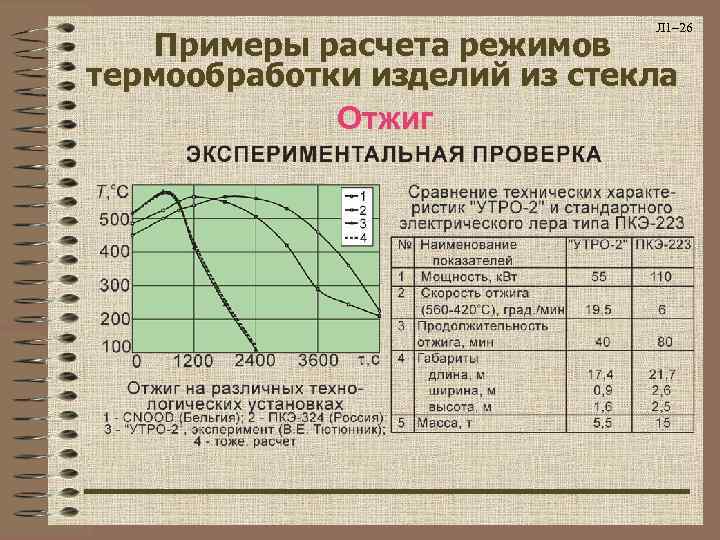
 Л 1– 26 Примеры расчета режимов термообработки изделий из стекла Отжиг
Л 1– 26 Примеры расчета режимов термообработки изделий из стекла Отжиг
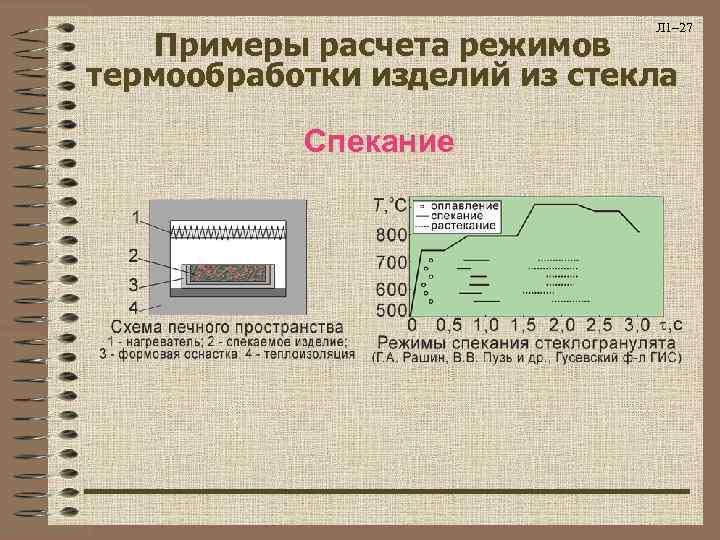
 Л 1– 27 Примеры расчета режимов термообработки изделий из стекла Спекание
Л 1– 27 Примеры расчета режимов термообработки изделий из стекла Спекание
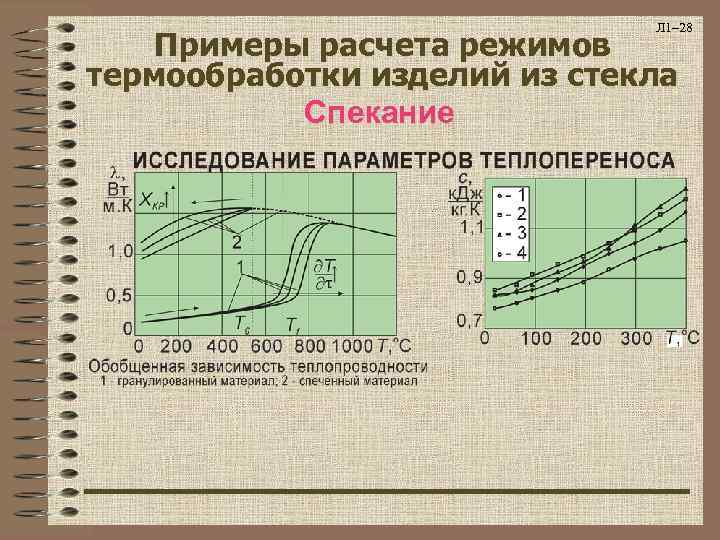
 Л 1– 28 Примеры расчета режимов термообработки изделий из стекла Спекание
Л 1– 28 Примеры расчета режимов термообработки изделий из стекла Спекание
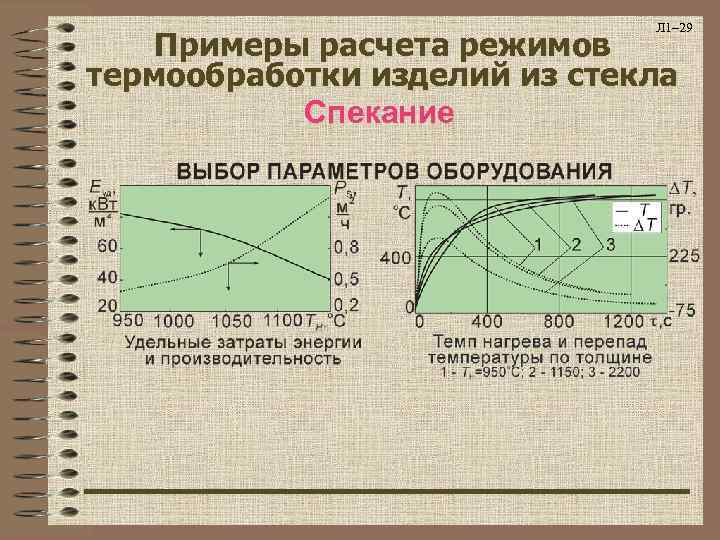
 Л 1– 29 Примеры расчета режимов термообработки изделий из стекла Спекание
Л 1– 29 Примеры расчета режимов термообработки изделий из стекла Спекание
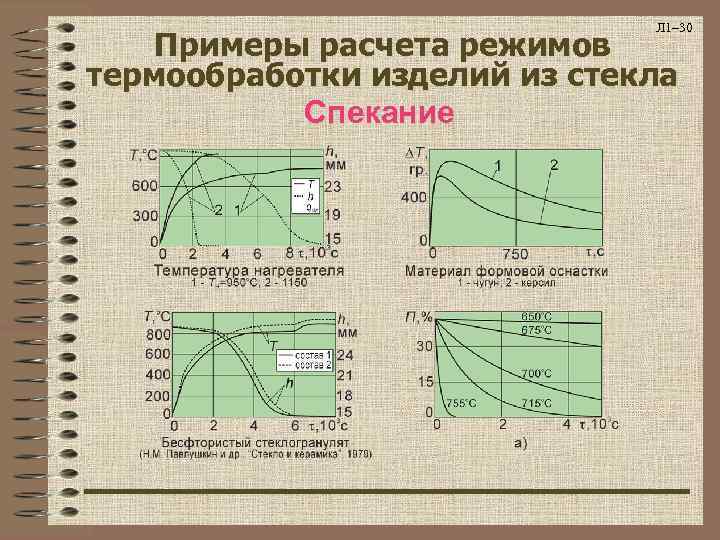
 Л 1– 30 Примеры расчета режимов термообработки изделий из стекла Спекание
Л 1– 30 Примеры расчета режимов термообработки изделий из стекла Спекание
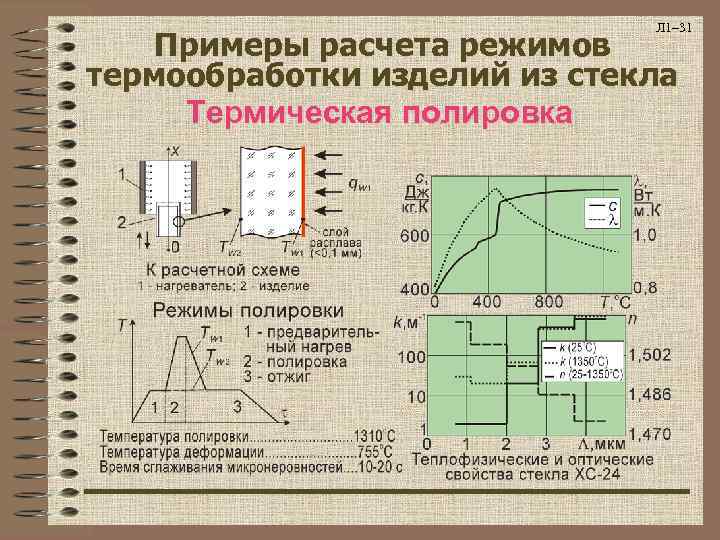
 Л 1– 31 Примеры расчета режимов термообработки изделий из стекла Термическая полировка
Л 1– 31 Примеры расчета режимов термообработки изделий из стекла Термическая полировка
 Примеры расчета режимов Л 1– 32 термообработки изделий из стекла Термическая полировка
Примеры расчета режимов Л 1– 32 термообработки изделий из стекла Термическая полировка
 Л 1– 33 Литература по теме 1. Тихонов А. Н. , Самарский А. А. Уравнения математической физики. -- М. : Наука, 1966. -- 724 с. 2. Калинин Д. Ю. Методические средства проектирования технологических процессов термообработки изделий из стекла. Дисс. канд. техн. наук. М. , 1999.
Л 1– 33 Литература по теме 1. Тихонов А. Н. , Самарский А. А. Уравнения математической физики. -- М. : Наука, 1966. -- 724 с. 2. Калинин Д. Ю. Методические средства проектирования технологических процессов термообработки изделий из стекла. Дисс. канд. техн. наук. М. , 1999.

