Тема лекции Теория вероятностей Содержание лекции 1 Вероятность

Тема лекции «Теория вероятностей» Содержание лекции 1. Вероятность события 2. Теорема сложения вероятностей 3. Теорема умножения вероятностей

Вероятность события В различных областях человеческой деятельности приходится иметь дело с событиями, которые невозможно точно предсказать. Поэтому приходится прогнозировать исход такой деятельности на основе собственного или чужого опыта, либо на основе интуиции, опирающейся на опытные данные.

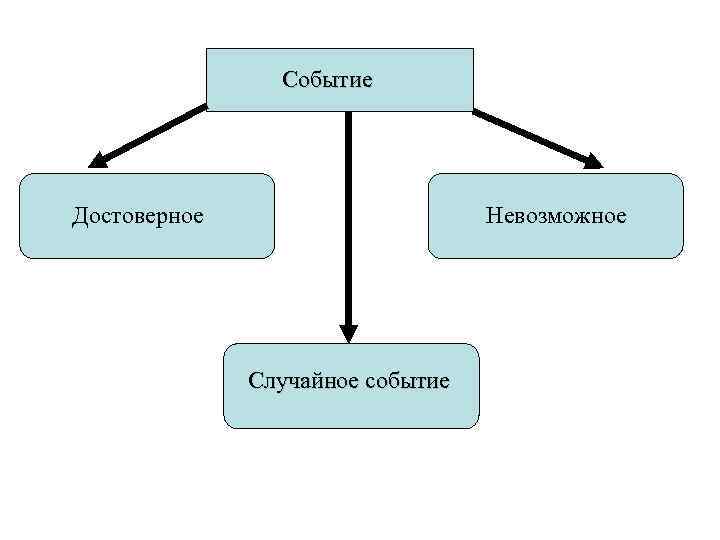Событие Достоверное Невозможное Случайное событие

Определения: Случайным называется событие, которое может произойти или не произойти в результате некоторого испытания Испытание (опыт, эксперимент) – это процесс, включающий определенные условия и приводящий к одному из нескольких возможных исходов. Исходом испытания может быть результат наблюдения или измерения. Единичный, отдельный исход испытания называется элементарным событием

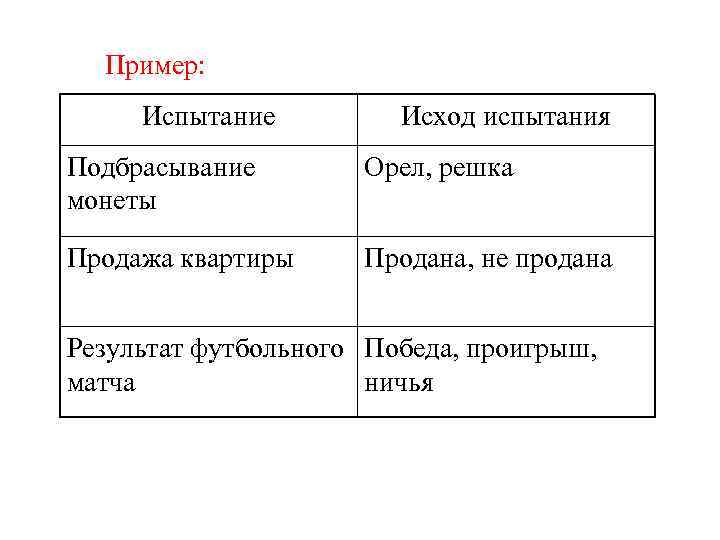Пример: Испытание Исход испытания Подбрасывание монеты Орел, решка Продажа квартиры Продана, не продана Результат футбольного Победа, проигрыш, матча ничья

Определение: Достоверным называется событие, обязательно появляющееся в результате опыта. Достоверные события обозначаются символом Пример: Извлечение из урны, содержащей только белые шары, белого шара.

Определение: Невозможным называется событие, которое не может произойти в результате опыта. Невозможные события обозначаются символом Пример: Извлечение из урны, содержащей только белые шары, черного шара. Достоверные и невозможные события не являются случайными.

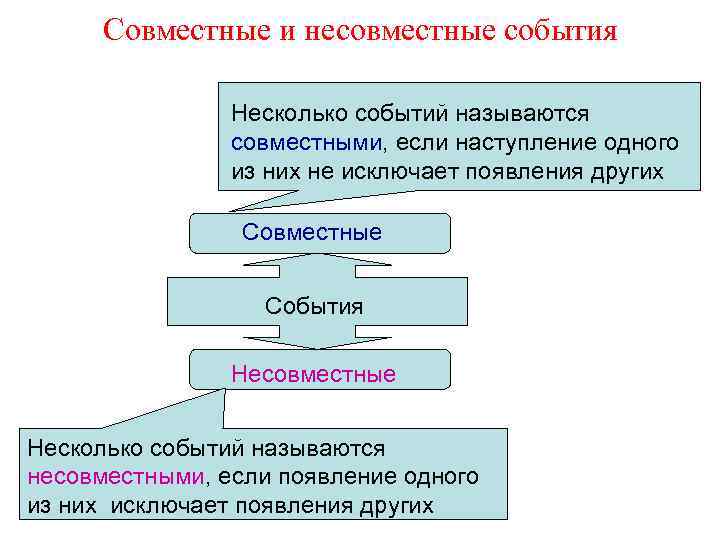Совместные и несовместные события Несколько событий называются совместными, если наступление одного из них не исключает появления других Совместные События Несовместные Несколько событий называются несовместными, если появление одного из них исключает появления других

Пример совместных событий Событие А – в магазин вошел покупатель старше 60 лет Событие В – в магазин вошла женщина События А и В совместны, так как в магазин может войти женщина старше 60 лет

Пример несовместных событий Событие А – выигрыш одной партии в шахматы Событие В – проигрыш одной партии в шахматы Событие С – ничейный исход одной партии в шахматы События А , В и С несовместны

ОПРЕДЕЛЕНИЕ События называются единственно возможными, если в результате испытания хотя бы одно из них произойдет ПРИМЕР Фирма рекламирует свой товар по радио и в газете. Единственно возможные события: - Потребитель услышит о товаре по радио; - Потребитель прочитает о товаре в газете; - Потребитель получит информацию о товаре по радио и в газете; - Потребитель не слышал о товаре по радио и не читал в газете.

Равновозможные события Определение Несколько событий называются равновозможными, если в результате испытания ни одно из них не имеет объективно большую возможность появления, чем другие. Пример При бросании игральной кости появление каждой из ее граней – события равновозможные.

Полная группа событий. Противоположные события Определения События образуют полную группу событий, если хотя бы одно из них обязательно произойдет в опыте. Два единственно возможных события, образующих полную группу, называются противоположными Пример: А – событие А Полная группа событий А А – противоположное событие

Алгебра событий Суммой событий называется событие, состоящее в появлении хотя бы одного из этих событий Произведением событий называется событие, состоящее в одновременном появлении всех этих событий

Вероятность события Вероятность является количественной мерой возможности появления события Классическое определение Вероятностью события А называют отношение числа благоприятствующих элементарных исходов (m ) к общему числу равновозможных элементарных исходов, образующих полную группу (n).

Пример . . . Рассматриваемое событие А – четное число очков на выпавшей грани игральной кости Общее число исходов (число граней) – 6 Число благоприятствующих исходов (грани содержащие 2, 4, 6 очков) – 3

Вероятность события Относительной частотой появления события А называется отношение числа испытаний m 1, при которых событие появилось, к общему числу произведенных испытаний n 1. Статистическое определение Вероятностью события А называется число, относительно которого устанавливается относительная частота W(A) при неограниченном увеличении числа опытов

Статистическое определение вероятности события При очень большом числе испытаний статистическая вероятность приближенно равна классической. В практических задачах за вероятность события принимается относительная частота при достаточно большом числе испытаний.

Свойства вероятности 1. Вероятность достоверного события равна 1. 2. Вероятность невозможного события равна 0. 3. Вероятность случайного события есть положительное число, заключенное между 0 и 1. 4. Сумма вероятностей противоположных событий равна 1.

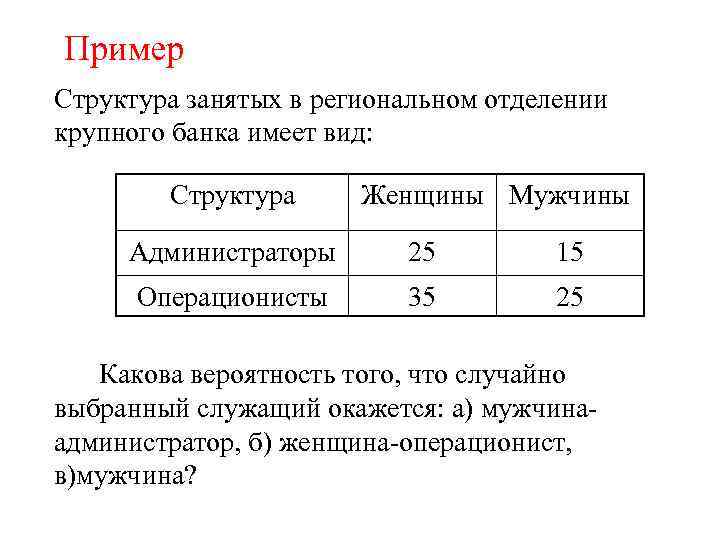Пример Структура занятых в региональном отделении крупного банка имеет вид: Структура Женщины Мужчины Администраторы 25 15 Операционисты 35 25 Какова вероятность того, что случайно выбранный служащий окажется: а) мужчинаадминистратор, б) женщина-операционист, в)мужчина?

Решение а) Событие А – случайно выбранный служащий – мужчина-администратор. Вычислим вероятность события А, используя классическое определение вероятности: Общее число исходов это численность работающих в банке служащих n=100. Число благоприятствующих исходов это численность мужчин-администраторов m=15. Тогда вероятность события А равна:

Решение б) Событие В – случайно выбранный служащий – женщина-операционист. Общее число исходов это численность работающих в банке служащих n=100. Число благоприятствующих исходов это численность женщин-операционисток m=35. Тогда вероятность события в равна:

Решение в) Событие С – случайно выбранный служащий – мужчина. Общее число исходов это численность работающих в банке служащих n=100. Число благоприятствующих исходов это численность мужчин m=40. Тогда вероятность события в равна:

Теорема сложения вероятностей несовместных событий Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий

Условная вероятность Определение Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А Если вероятность события А рассматривается при условии, что произошли два других события В и С, используется условная вероятность относительно произведения событий В и С

Теорема умножения вероятностей Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место Пример: В магазине 35 компьютеров, 5 из них с дефектами. Найти вероятность того, два наугад взятых компьютера без дефектов. Решение: А – первый наугад взятый компьютер без дефекта В - второй наугад взятый компьютер без дефекта, при условии, что первый компьютер без дефекта

Независимые и зависимые события Определение События А и В называются независимыми, если при наступлении события А вероятность события В не меняется. Для независимых событий События А и В называются зависимыми, если вероятность каждого из них зависит от того произошло или нет другое событие.

Теорема сложения вероятностей совместных событий Вероятность суммы двух совместных событий А и В равна сумме вероятностей этих событий без вероятности их совместного наступления

Вероятность появления хотя бы одного события Если события независимы в совокупности, тогда вероятность появления события А, состоящего в появлении хотя бы одного из событий равна:

Пример Студент пришел на экзамен, выучив 15 вопросов из 25. Экзаменатор задал студенту 3 вопроса. Какова вероятность того, что студент ответит на все 3 вопроса? Решение: Событие А – студент знает все 3 вопросазаключается в совместном наступлении событий: - студент знает 1 -й вопрос; - студент знает 2 -й вопрос; - студент знает 3 -й вопрос. События , , - зависимые

Решение Вычислим вероятности событий Тогда вероятность того, что студент ответит на все 3 вопроса, равна:

Тема «Основные формулы для вычисления вероятностей событий» Содержание 1. Формула полной вероятности 2. Формула Байеса 3. Формула Бернулли 4. Формула Пуассона

Формула полной вероятности Пусть событие В может произойти только с одним из несовместных событий , называемых гипотезами. Событие В можно рассматривать как

Формула полной вероятности По теореме сложения вероятностей: Используя теорему умножения вероятностей получим формулу полной вероятности:

Пример: Эксперт полагает, что вероятность роста стоимости акций компании в следующем году будет 0. 75, если экономика страны будет на подъеме, и 0. 3, если экономика не будет успешно развиваться. По его мнению, вероятность экономического подъема в следующем году- 0. 8. Оцените вероятность того, что акции компании поднимутся в цене в следующем году.

Решение: Событие В- акции компании поднимутся в цене в следующем году. Событие В может произойти вместе с одной из гипотез: - экономика страны на подъеме - экономика не будет успешно развиваться По условию известны вероятности гипотез и условные вероятности события В

Решение: Для решения задачи применяем формулу полной вероятности:

Формула Байеса Пусть событие В происходит с одним из n несовместных событий Эти события образуют полную группу. Формула Байеса позволяет найти вероятность события , если известно, что событие В произошло:

Формула Бернулли Проводится n независимых испытаний. Необходимо определить вероятность того, что в m испытаниях наступит событие А. Вероятность наступления события А в каждом испытании – р. По формуле Бернулли определяется - вероятность того, что в n испытаниях событие А произойдет m раз

Формула Пуассона Используется при большом числе испытаний n и малой вероятности р.

Тема «Дискретные случайные величины» Содержание 1. Виды случайных величин 2. Распределение дискретной случайной величины 3. Математическое ожидание и его свойства 4. Дисперсия и ее свойства 5. Распределение Бернулли и Пуассона

Виды случайных величин Определения: Величина называется случайной, если в результате опыта она может принять любое заранее неизвестное значение. Случайные величины делятся на дискретные и непрерывные. Величина называется дискретной, если она может принимать определенные, фиксированные значения. Величина называется непрерывной, если она может принимать значения, сколь угодно мало отличающиеся друг от друга. Обозначение случайной величины: X, Y….

Распределение дискретной случайной величины Дискретная случайная величина X может принимать значения с вероятностями Определение: Соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения дискретной случайной величины

Распределение дискретной случайной величины Дискретная случайная величина X может быть задана функцией распределения Определение: Функцией распределения случайной величины X называется функция F(x), выражающая вероятность того, что X примет значение, меньшее чем x.

Основные свойства функции распределения 1. Функция распределения – неубывающая функция своего аргумента 2. На минус бесконечности функция распределения равна нулю 3. На плюс бесконечности функция распределения равна единице

Распределение дискретной случайной величины

Математическое ожидание и его свойства Одной из важных числовых характеристик случайной величины X является математическое ожидание: М(Х) – среднее ожидаемое значение случайной величины Свойства: 1. 2. 3. , если Х, У-любые 4. , если Х, У -независимы

Дисперсия и ее свойства Дисперсией случайной величины X называется математическое ожидание квадрата разности (Х-М(Х)): Понятие дисперсии вводят для оценки степени рассеяния значения случайной величины около ее среднего значения М(Х). Свойства: 1. 2. 3. , если Х, У- независимы

Среднее квадратическое отклонение определяется как квадратный корень из дисперсии: Размерность величин совпадает с размерностью самой случайной величины Х Свойства: 1. 2. 3. Формула для вычисления дисперсии: , если Х, У- независимы

Распределение Бернулли Проводится n независимых испытаний. Вероятность наступления события А в каждом испытании – , а вероятность не наступления По формуле Бернулли определяется - вероятность того, что в n испытаниях событие А произойдет m раз. Определение: Биномиальным называют закон распределения величины Х – числа появлений события в n независимых испытаниях, в каждом из которых вероятность наступления события равна , а вероятности возможных значений X=1, 2, 3……m, ……n вычисляются по формуле Бернулли

Распределение Бернулли Число успехов Х 0 1 … Вероятность Числовые характеристики биномиального распределения: n

Распределение Пуассона Если число испытаний n велико, а вероятность р мала, используется формула Пуассона Закон распределения Пуассона Число успехов Х Вероятность 0 1 … n

Тема «Непрерывные случайные величины» 1. 2. 3. 4. 5. Содержание Функция и плотность распределения вероятностей. Математическое ожидание и дисперсия. Равномерное распределение Экспоненциальное распределение Нормальное распределение. Функция Лапласа

Функция распределения вероятностей Для характеристики непрерывной случайной величины используется функция распределения вероятностей, выражающая вероятность того, что случайная величина X примет значение, меньшее чем x.

Плотность распределения Функция называется плотностью распределения непрерывной случайной величины Х Основные свойства плотности распределения 1. 2.

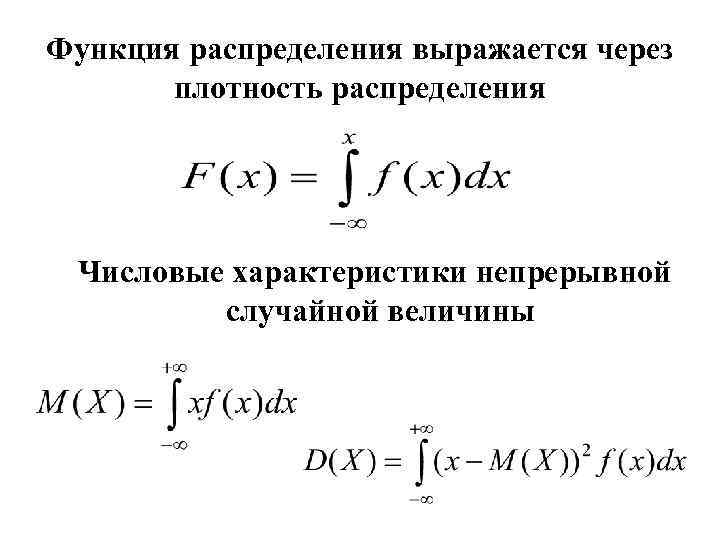Функция распределения выражается через плотность распределения Числовые характеристики непрерывной случайной величины

Экспоненциальное распределение Определение Экспоненциальным (показательным) распределением непрерывной случайной величины Х называется такое распределение, которое описывается следующим выражением для плотности вероятности:

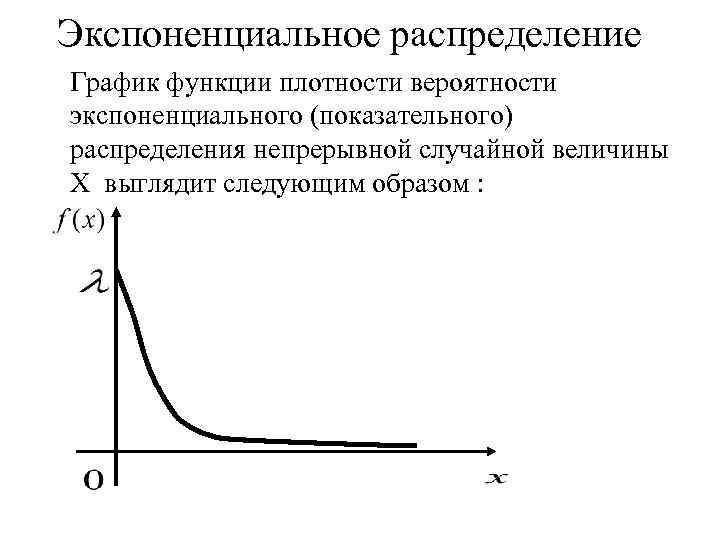Экспоненциальное распределение График функции плотности вероятности экспоненциального (показательного) распределения непрерывной случайной величины Х выглядит следующим образом :

Экспоненциальное распределение Функция распределения имеет вид:

Числовые характеристики экспоненциального распределения Математическое ожидание: Дисперсия:

Нормальное распределение Определение Нормальным распределением непрерывной случайной величины Х называется такое распределение, плотность вероятности которого описывается функцией : - закон Гаусса

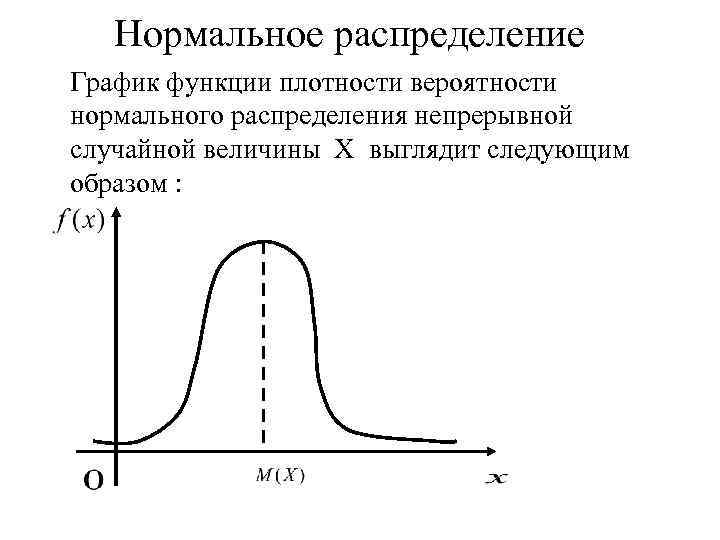Нормальное распределение График функции плотности вероятности нормального распределения непрерывной случайной величины Х выглядит следующим образом :

Нормированное нормальное распределение Определение Если параметры нормального распределения непрерывной случайной величины Х то получаем распределение называемое нормированным нормальным распределением, плотность вероятности которого описывается функцией :

Вероятность попадания в заданный интервал Для случайной величина распределенной по нормальному закону Где - функция Лапласа

Свойства функции Лапласа 1. 2. 3. Функция Лапласа табулирована

Правило трех сигм С вероятностью 0, 9973 случайная величина Х, распределенная по нормальному закону удовлетворяет неравенству: Если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает