ТЕМА ЛЕКЦИИ: J ПР ОД ОЛ Ж ЕН И Е
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Определение: Случайной величиной называют величину, которая в результате испытания примет какое-либо одно возможное значение, но заранее не известно, какое именно. Пример. Диаметр изготавливаемой на токарном станке детали – случайная величина, т. к. возможны отклонения из-за возникающих погрешностей ввиду температурных изменений, силы трения, биений, неоднородности материала и т. д. . Таким образом диаметр принадлежит некоторому промежутку (c, d).
ТИПЫ СЛУЧАЙНЫХ ВЕЛИЧИН Определение: Непрерывной случайной величиной (НСВ) называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Множество возможных значений непрерывной случайной величины бесконечно и несчетно. Определение: Дискретной случайной величиной (ДСВ) называют такую случайную величину, которая может принимать отдельные, изолированные значения из множества возможных. Множество значений дискретной случайной величины либо конечное, либо бесконечное, но счетное.
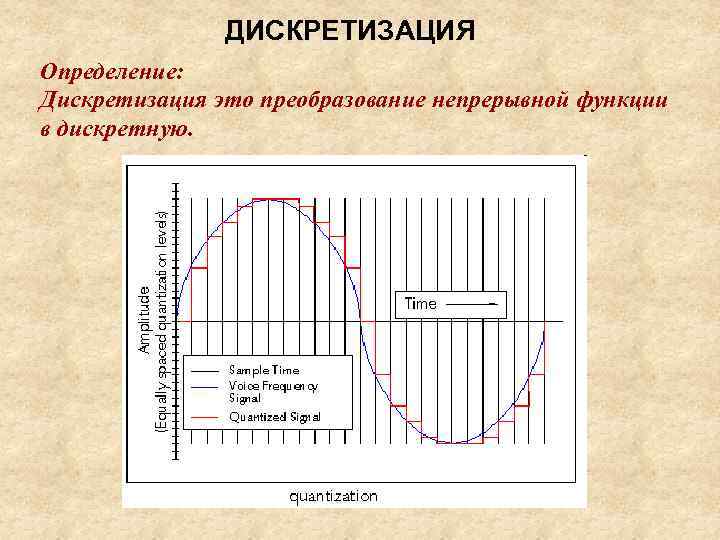ДИСКРЕТИЗАЦИЯ Определение: Дискретизация это преобразование непрерывной функции в дискретную.
ПОНЯТИЕ РАСПРЕДЕЛЕНИЯ Определение: Распределением случайной величины называют зависимость между возможным значением данной случайной величины и вероятностью принятия этого значения. Виды распределений: • Ряд распределения. • Функция распределения.
РЯД РАСПРЕДЕЛЕНИЯ При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая - их вероятности: x 1 x 2 x 3 … xn p 1 p 2 p 3 … pn Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события Х=х1, Х=х2, …, Х=хn – образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице.
ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ (что за ерунда? ? ? ) Если случайная величина является непрерывной, то зависимость между возможным значением данной величины и ее вероятностью является функцией распределения.
ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ (а вот это мы где-то видели? )
Считая, что для каждого малого участка допустимых значений случайной величины X вероятность попадания на него значения рассматриваемой случайной величины пропорциональна длине этого участка, можно охарактеризовать случайную величину X, указав вероятность p(x)dx того, что x < X < x + dx. р(х) – вероятность, которая приходится на единицу длины рассматриваемого участка. Определение: Функцию р(х) называют плотностью распределения вероятностей или дифференциальной функцией распределения.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ Определение: Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения равна:
Центральная предельная теорема Чебышева: Если случайная величина подвержена воздействию бесконечного числа бесконечно малых случайных факторов, то она имеет нормальное распределение. Нормальный закон распределения является предельным законом, к которому приближаются другие законы распределения при часто встречающихся аналогичных условиях. Если предоставляется возможность рассматривать некоторую случайную величину, как сумму достаточно большого числа других случайных величин, то данная случайная величина обычно подчиняется нормальному закону распределения.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ В ПРИРОДЕ Распределение частоты попадания в мишень в зависимости от удаления от центра.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ Определение: Математическим ожиданием М(Х) дискретной случайной величины называется сумма произведений возможных значений на вероятности принятия этих значений. n Выражается формулой: Свойство 1. Мат. ожидание суммы случайных величин равно сумме их мат. ожиданий: Свойство 2. Математическое ожидание произведения независимых случайных величин Х и Y равно произведению математических ожиданий этих вел. M(XY)=M(X)·M(Y).
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ Определение: Математическое ожиданием М(Х) называется средняя величина возможных значений случайных величин, взвешенных по их вероятности. Выражается формулой: b M(X)= a
ДИСПЕРСИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Определение: Дисперсия дискретной случайной величины – это есть среднее арифметическое из квадратов отклонений от математического ожидания. D(X)= /n
ДИСПЕРСИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Определение: Дисперсией непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называется определенный интеграл b D(X)= a D(X)= σ2(X) σ(X)= σ(X) – среднеквадратичное отклонение случайной величины Х.
Стандартное (среднеквадратичное) отклонение D(X)= σ2(X) σ(X)=
ЛИТЕРАТУРА http: //igriki. narod. ru/norm_zak_raspr 1. htm http: //chemstat. com. ru/node/8 http: //www. tspu. tula. ru/res/math/mop/lections/lection_2. htm http: //apollyon 1986. narod. ru/docs/TVi. MS/NP/lekziitv/lekziya 8. htm http: //apollyon 1986. narod. ru/docs/TVi. MS/NP/lekziitv/lekziya 9. htm http: //www. realcoding. net/teach/SPSS/Glava%205/Index 4. html http: //www. tech-e. ru/2008_6_28. php http: //www. mathematics. ru/courses/algebra/content/chapter 4/section 3/paragraph 5/theory. html http: //www. toehelp. ru/theory/ter_ver/3_5/