Скачать презентацию Тема лекции 1 Классы динамических моделей 2 Скачать презентацию Тема лекции 1 Классы динамических моделей 2

Лекция 13 - Эконометрик.pptx

  • Количество слайдов: 40

Тема лекции: Тема лекции:

1. Классы динамических моделей 2. Модели с распределёнными лагами 3. Пример 4. Оценка параметров 1. Классы динамических моделей 2. Модели с распределёнными лагами 3. Пример 4. Оценка параметров моделей с распределенными лагами 5. Полиномиально распределённые лаги Алмон 6. Пример модели с распределёнными лагами

1. Классы динамических моделей В моделях временных рядов зависимая переменная yt может быть связана 1. Классы динамических моделей В моделях временных рядов зависимая переменная yt может быть связана не только со значениями объясняемых переменных х в момент времени t, но и с их значениями в предыдущие моменты времени. Так , например, потребление товаров длительного пользования зачастую зависит не только от доходов текущего, но и предыдущего.

1. Классы динамических моделей Модели регрессии по временным рядам с лаговыми переменными принято называть 1. Классы динамических моделей Модели регрессии по временным рядам с лаговыми переменными принято называть динамическими моделями. Их можно подразделить на три класса: 1. модели с лаговыми объясняющими переменными, или, иначе, модели с распределенными лагами: yt = a + boxt + b 1 xt-1 + … +bk xt-k + Ɛt ; 2. модели с лаговыми зависимыми переменными – модели авторегрессии: yt = a + bxt + c 1 yt-1 + … +ck yt-k + Ɛt ; 3. модели с лаговыми зависимыми и независимыми переменными, т. е. авторегрессионные модели с распределенными лагами: yt = a + b 1 yt -1 + …+ bk yt-k + coxt + c 1 xt-1 + … +ck xt-k + Ɛt ;

1. Классы динамических моделей Центральным вопросом при построении моделей с лаговыми переменными является выбор 1. Классы динамических моделей Центральным вопросом при построении моделей с лаговыми переменными является выбор величины лага и числа лаговых переменных. Теоретически трудно определить величину лага. Определенную помощь может оказать взаимная корреляционная функция: рассчитывается множество коэффициентов корреляции между уровнями временных рядов (yt ) и (xt ), сдвинутыми относительно друга на последовательно увеличивающиеся интервалы времени. Величина лага определяется по максимальному значению коэффициента корреляции.

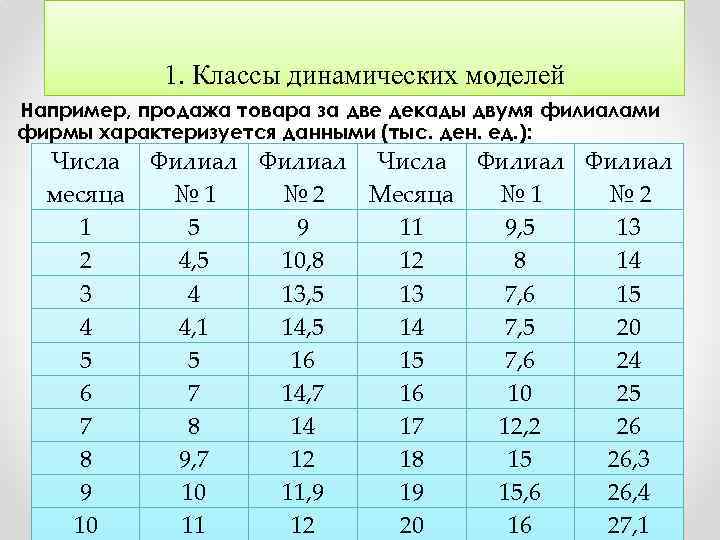1. Классы динамических моделей Например, продажа товара за две декады двумя филиалами фирмы характеризуется 1. Классы динамических моделей Например, продажа товара за две декады двумя филиалами фирмы характеризуется данными (тыс. ден. ед. ): Числа месяца 1 2 3 4 5 6 7 8 9 10 Филиал Числа Филиал № 1 № 2 Месяца № 1 № 2 5 9 11 9, 5 13 4, 5 10, 8 12 8 14 4 13, 5 13 7, 6 15 4, 1 14, 5 14 7, 5 20 5 16 15 7, 6 24 7 14, 7 16 10 25 8 14 17 12, 2 26 9, 7 12 18 15 26, 3 10 11, 9 19 15, 6 26, 4 11 12 20 16 27, 1

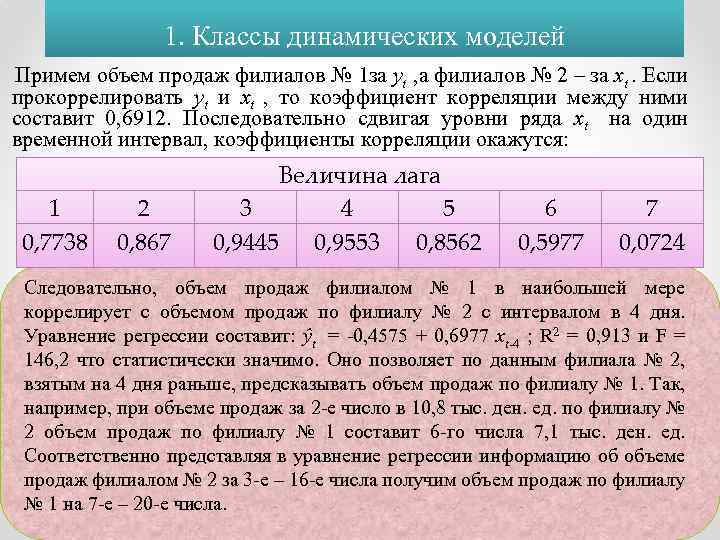1. Классы динамических моделей Примем объем продаж филиалов № 1 за yt , а 1. Классы динамических моделей Примем объем продаж филиалов № 1 за yt , а филиалов № 2 – за xt. Если прокоррелировать yt и xt , то коэффициент корреляции между ними составит 0, 6912. Последовательно сдвигая уровни ряда xt на один временной интервал, коэффициенты корреляции окажутся: 1 0, 7738 2 0, 867 Величина лага 3 4 5 0, 9445 0, 9553 0, 8562 6 0, 5977 7 0, 0724 Следовательно, объем продаж филиалом № 1 в наибольшей мере коррелирует с объемом продаж по филиалу № 2 с интервалом в 4 дня. Уравнение регрессии составит: ŷt = -0, 4575 + 0, 6977 xt-4 ; R 2 = 0, 913 и F = 146, 2 что статистически значимо. Оно позволяет по данным филиала № 2, взятым на 4 дня раньше, предсказывать объем продаж по филиалу № 1. Так, например, при объеме продаж за 2 -е число в 10, 8 тыс. ден. ед. по филиалу № 2 объем продаж по филиалу № 1 составит 6 -го числа 7, 1 тыс. ден. ед. Соответственно представляя в уравнение регрессии информацию об объеме продаж филиалом № 2 за 3 -е – 16 -е числа получим объем продаж по филиалу № 1 на 7 -е – 20 -е числа.

1. Классы динамических моделей Выбор величины лага и количества лагов проводится обычно экспериментально: строятся 1. Классы динамических моделей Выбор величины лага и количества лагов проводится обычно экспериментально: строятся модели с разным числом лагов и их величиной и изучается значимость коэффициентов регрессии при лаговых переменных; останавливаются на модели, для которой все коэффициенты регрессии при лаговых переменных будут статистически значимыми по t-критерию Стьюдента.

1. Классы динамических моделей Построение моделей с лаговыми переменными имеет свою специфику. Дело не 1. Классы динамических моделей Построение моделей с лаговыми переменными имеет свою специфику. Дело не только в выборе величины лага и их числа. Во многих случаях оценка параметров моделей с лаговыми переменными не может быть проведена с помощью традиционного МНК ввиду нарушения ряда его предпосылок и требует специальных методов оценивания. При наличии двух и более лаговых переменных возникает проблема мультиколлинеарности факторов, ибо, как правило, xt , xt-1, xt-2, . . . xt-k или yt-1, yt-2, …yt-k связаны между собой, особенно при наличии тенденции в рядах динамики. Это снижает точность оценок коэффициентов при лаговых переменных и требует видоизменять приемы оценивания.

2. Модели с распределёнными лагами Модели с распределенными лагами бывают двух типов: 1. с 2. Модели с распределёнными лагами Модели с распределенными лагами бывают двух типов: 1. с конечным числом лагов: yt = a + boxt + b 1 xt-1 + … +bk xt-k + Ɛt ; 2. с бесконечным числом лагов: yt = a + boxt + b 1 xt-1 + b 2 xt-2 + … + Ɛt ; Практическое применение чаще имеют модели с конечным числом лагов, т. е. модели, в которых число лагов экспериментально определено.

2. Модели с распределёнными лагами Предположим рассматривается модель, в которой k = 4, т. 2. Модели с распределёнными лагами Предположим рассматривается модель, в которой k = 4, т. е. ŷt = a + boxt + b 1 xt-1 + b 2 xt-2 + b 3 xt-3 + b 4 xt-4. Данная модель означает, что изменение во времени t объясняющей переменной x будет влиять на значение результативного признака y в течение 4 следующих моментов времени. Коэффициент bo называют краткосрочным мультипликатором, так как он характеризует среднее изменение результата у при изменении xt на 1 единицу своего измерения в фиксированный момент времени t. В момент времени t + 1 воздействие объясняющей переменной х на результат у составит (bo + b 1 ) единиц, а в момент времени t + 2 общее изменение у составит (bo + b 1 + b 2 ) единиц.

2. Модели с распределёнными лагами Любую сумму коэффициентов j , где (h < k) 2. Модели с распределёнными лагами Любую сумму коэффициентов j , где (h < k) называют промежуточным мультипликатором, а сумму всех коэффициентов регрессии j - долгосрочным мультипликатором, который характеризует общее изменение у через k интервалов времени под воздействием изменения х в момент t на 1 единицу. При k = 4 долгосрочный мультипликатор составит bo + b 1 + b 2 + b 3 + b 4. Он характеризует общее среднее изменение у через 4 временных интервала при увеличении х в момент времени t на 1 единицу, а промежуточные мультипликаторы: bo + b 1 - изменение у в момент времени t + 1; bo + b 1 + b 2 - изменение у в момент времени t + 2; bo + b 1 + b 2 + b 3 - изменение у в момент времени t + 3.

2. Модели с распределёнными лагами Если все коэффициенты регрессии имеют одинаковые знаки, т. е. 2. Модели с распределёнными лагами Если все коэффициенты регрессии имеют одинаковые знаки, т. е. характеризуются однонаправленным изменением у в исследуемые k моментов времени, то можно определять относительные коэффициенты модели βj , т. е. βj = bj / ∑ bj , где 0 < βj < 1, а ∑ βj = 1. Иными словами, βj характеризует долю общего изменения у в момент времени t + j.

3. Пример Предположим, что регрессия основных производственных фондов (y- млн руб. ) в зависимости 3. Пример Предположим, что регрессия основных производственных фондов (y- млн руб. ) в зависимости от размера инвестиций (x- млн руб. ) характеризуется уравнением ŷt = 0, 8+0, 7 xt+1, 0 xt-1+1, 5 xt-2+0, 6 xt-3+0, 2 xt-4, где t- года.

Анализ уравнения показывает, что рост инвестиций на 1 млн руб. в текущем периоде приводит Анализ уравнения показывает, что рост инвестиций на 1 млн руб. в текущем периоде приводит к росту основных производственных фондов: в том же периоде на 0, 7 млн руб. (краткосрочный мультипликатор); через 1 год на 0, 7+1 = 1, 7 млн руб. ; через 2 года на 0, 7+1+1, 5 = 3, 2 млн руб. ; через 3 года на 3, 8 млн руб. (промежуточный, как и предыдущие два, мультипликатор); через 4 года на 4 млн руб. (долгосрочный мультипликатор).

Относительные коэффициенты модели составят: β 0 = 0, 7/4 = 0, 175; β 1 Относительные коэффициенты модели составят: β 0 = 0, 7/4 = 0, 175; β 1 = 1/4 = 0, 25; β 2 = 1, 5/4 = 0, 375; β 3 = 0, 6/4 = 0, 15; β 4 = 0, 2/4 = 0, 05. Следовательно, в текущем году реализуется 17, 5% воздействия увеличения инвестиций на рост основных производственных фондов, а через год – еще 25%. Через 2 года – еще 37, 5%, через 3 года – еще 15% и через 4 года – еще 5%.

4. Оценка параметров моделей с распределенными лагами Модель с конечным числом лагов при правильной 4. Оценка параметров моделей с распределенными лагами Модель с конечным числом лагов при правильной ее спецификации может быть оценена обычным МНК. В этом случае в уравнении: yt = a + boxt + b 1 xt-1 + b 2 xt-2 + … + bk xt-k + Ɛt переменные xt, xt-1, …, xt-k рассматриваются как объясняющие переменные обычной множественной регрессии.

Вместе с тем применение МНК к моделям с конечным числом лагов может быть реально Вместе с тем применение МНК к моделям с конечным числом лагов может быть реально затруднено ввиду следующих причин: 1. при наличии тенденции переменные xt, xt-1, …, xt-k тесно связаны между собой, что вызывает мультиколлинеарность факторов, которая может привести к неинтерпретируемым знакам y коэффициентов регрессии и к снижению их точности; 2. возможна автокорреляция остатков, так как МНК применяется к временным рядам с тенденцией.

Поэтому нередко для оценки параметров модели с распределяемым конечным числом лагов используются специальные методы Поэтому нередко для оценки параметров модели с распределяемым конечным числом лагов используются специальные методы преобразования, как и для модели с бесконечным числом лагов. Разработаны разные методы оценивания параметров моделей с распределенными лагами, которые учитывают характер распределения коэффициентов регрессии при лаговых объясняющих переменных. Иными словами, методы оценивания параметров модели с распределенными лагами основаны на изучении структуры лага. Так, предполагая полиномиальное распределение лаговых коэффициентов, используется метод Алмон, а при гипотезе геометрической прогрессии для лаговых коэффициентов применяется преобразование Койка.

5. Полиномиально распределённые лаги Алмон В 1965 г. Ширли Алмон предложила способ оценки параметров 5. Полиномиально распределённые лаги Алмон В 1965 г. Ширли Алмон предложила способ оценки параметров модели с распределёнными лагами на основе гипотезы, что лаговые коэффициенты регрессии аппроксимируют полиномом соответствующей степени от величины лага.

Предположим, что bj имеет распределение в виде параболы второй степени, т. е. bj = Предположим, что bj имеет распределение в виде параболы второй степени, т. е. bj = co + c 1 j + c 2 j 2 Тогда каждый из коэффициентов можно представить как: • bo= co ; • b 1= co+ c 1 + c 2 ; • b 2 = co+ 2 c 1 + 4 c 2 ; • b 3 = co+ 3 c 1 + 9 c 2 ; • …………………; • bk = co+ kc 1 + k 2 c 2.

Подставим эти соотношения для bj в модель с распределёнными лагами: yt = a + Подставим эти соотношения для bj в модель с распределёнными лагами: yt = a + co xt + (co+ c 1 + c 2) xt-1 + (co+ 2 c 1 + 4 c 2) xt-2 + + (co+ 3 c 1 + 9 c 2) xt-3 + … + (co+ kc 1 + k 2 c 2) xt-k + Ɛt Перегруппируем слагаемые с одинаковыми значениями с : yt = a + co (xt + xt-1 + xt-2 + … + xt-k) + c 1 (xt-1 + 2 xt-2 + 3 xt-3 + + … + k xt-k) + c 2 (xt-2 + 4 xt-3 + 9 xt-4 + … + k 2 xt-k) + Ɛt

Будем рассматривать слагаемые в скобках при co, c 1 и c 2 как новые Будем рассматривать слагаемые в скобках при co, c 1 и c 2 как новые переменные z, т. е. модель c распределёнными лагами примет вид: yt = a + cozo + c 1 z 1 + c 2 z 2 + Ɛt , где zo, z 1 и z 2 определяются как •

Оценка параметров при преобразовании переменных z даётся традиционным МНК. При этом случайные отклонения Ɛt Оценка параметров при преобразовании переменных z даётся традиционным МНК. При этом случайные отклонения Ɛt удовлетворяют предпосылкам МНК. Далее на основе параметров co , c 1 и c 2 переходим к оценке параметров bj , используя выражения коэффициентов через коэффициенты полинома: bj = co+ c 1 j + c 2 j 2 В общем виде при степени полинома m модель регрессии с распределёнными лагами составит yt = a + co(xt + xt-1 + xt-2 + … + xt-k) + c 1 (xt-1 + 2 xt-2 + 3 xt-3 + … + k xt-k) + c 2 (xt-2 + 4 xt-3 + 9 xt-4 + … + k 2 xt-k) + … + cm (xt-1 + 2 m xt-2 + 3 m xt-3 + … + km xt-k) + Ɛt или иначе: yt = a + co zo + c 1 z 1 + c 2 z 2 + … + cm zm + Ɛt

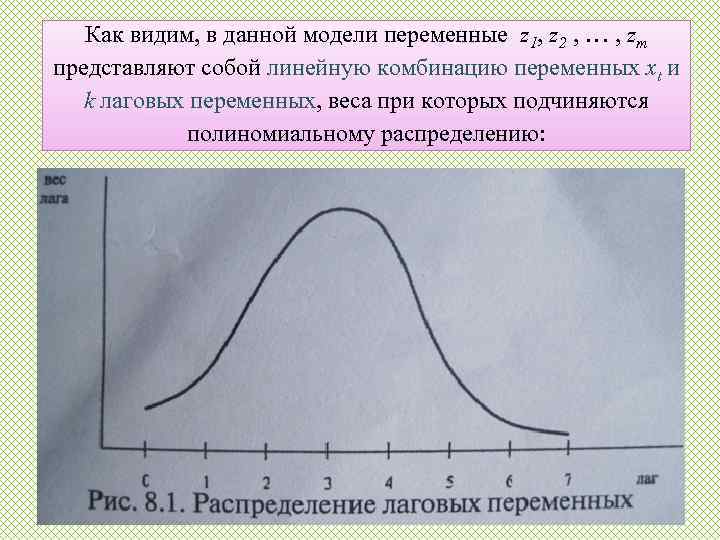Как видим, в данной модели переменные z 1, z 2 , … , zm Как видим, в данной модели переменные z 1, z 2 , … , zm представляют собой линейную комбинацию переменных xt и k лаговых переменных, веса при которых подчиняются полиномиальному распределению:

В матричном виде можно записать, что b=Hc , где 1 0 0 … … В матричном виде можно записать, что b=Hc , где 1 0 0 … … … 0 1 1 1 … … … 1 Н= 1 2 4 … … … 2 m 1 3 9 … … … 3 m … … ……… 1 k k 2 … … … km c - вектор коэффициентов при переменных z. - матрица весов при лаговых коэффициентах bj

Тогда модель в целом виде принимает вид y = XHc + Ɛ = Zc Тогда модель в целом виде принимает вид y = XHc + Ɛ = Zc + Ɛ Стандартная ошибка коэффициентов регрессии при лаговых переменных определяется как Далее через t -критерий Стьюдента оценивается значимость коэффициентов bj. Качество модели оценивается через коэффициент детерминации R 2 для уравнения регрессии yt от преобразованных переменных z, т. е. по модели y = Zc + Ɛ

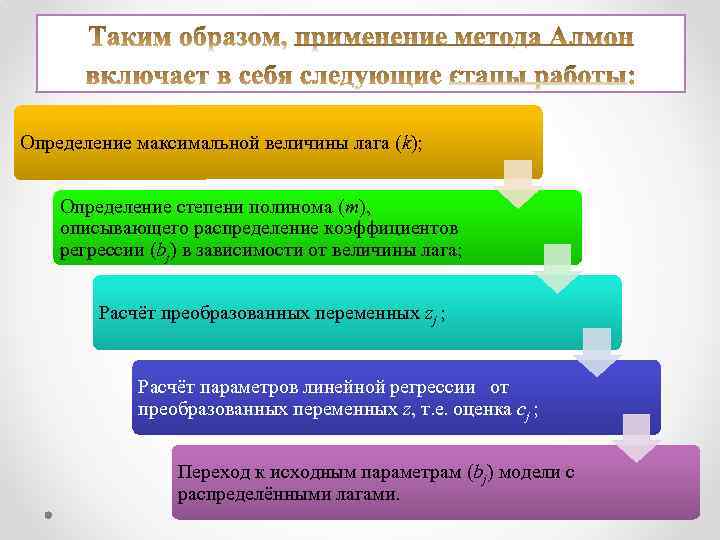Определение максимальной величины лага (k); Определение степени полинома (m), описывающего распределение коэффициентов регрессии (bj) Определение максимальной величины лага (k); Определение степени полинома (m), описывающего распределение коэффициентов регрессии (bj) в зависимости от величины лага; Расчёт преобразованных переменных zj ; Расчёт параметров линейной регрессии от преобразованных переменных z, т. е. оценка cj ; Переход к исходным параметрам (bj) модели с распределёнными лагами.

6. Пример модели с распределёнными лагами 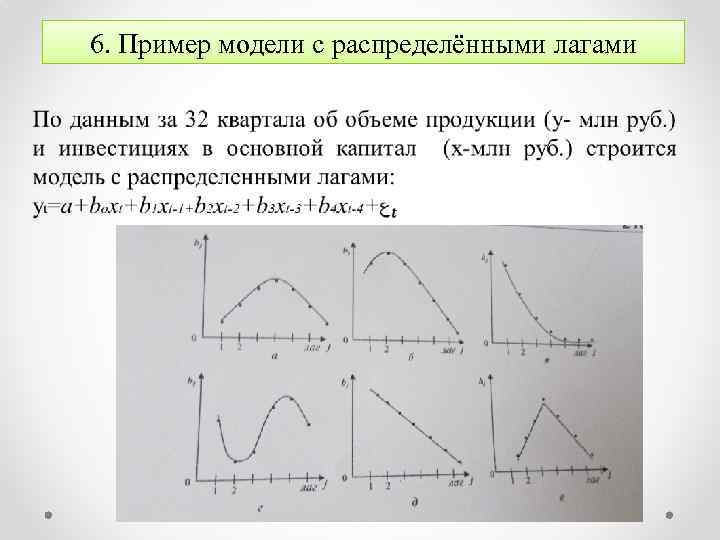• 6. Пример модели с распределёнными лагами •

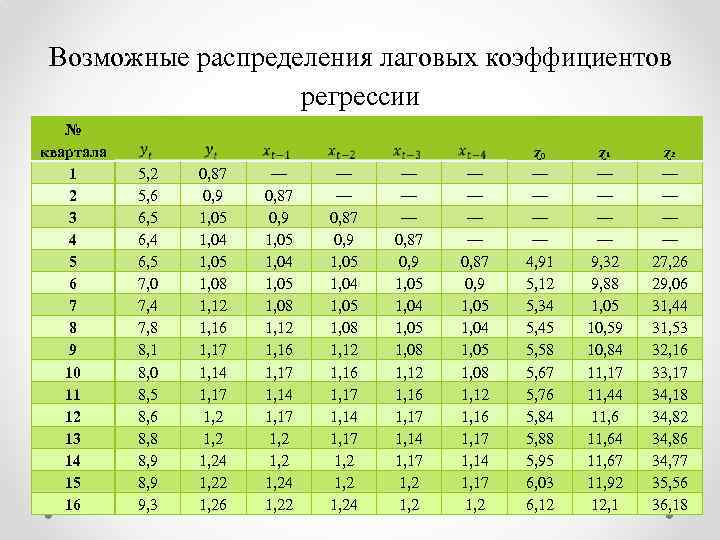Возможные распределения лаговых коэффициентов регрессии № квартала 1 2 3 4 5 6 7 Возможные распределения лаговых коэффициентов регрессии № квартала 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 5, 2 5, 6 6, 5 6, 4 6, 5 7, 0 7, 4 7, 8 8, 1 8, 0 8, 5 8, 6 8, 8 8, 9 9, 3 0, 87 0, 9 1, 05 1, 04 1, 05 1, 08 1, 12 1, 16 1, 17 1, 14 1, 17 1, 24 1, 22 1, 26 — 0, 87 0, 9 1, 05 1, 04 1, 05 1, 08 1, 12 1, 16 1, 17 1, 14 1, 17 1, 24 1, 22 — — 0, 87 0, 9 1, 05 1, 04 1, 05 1, 08 1, 12 1, 16 1, 17 1, 14 1, 17 1, 24 — — — 0, 87 0, 9 1, 05 1, 04 1, 05 1, 08 1, 12 1, 16 1, 17 1, 14 1, 17 1, 2 ɀₒ — — 4, 91 5, 12 5, 34 5, 45 5, 58 5, 67 5, 76 5, 84 5, 88 5, 95 6, 03 6, 12 ɀ₁ — — 9, 32 9, 88 1, 05 10, 59 10, 84 11, 17 11, 44 11, 64 11, 67 11, 92 12, 1 ɀ₂ — — 27, 26 29, 06 31, 44 31, 53 32, 16 33, 17 34, 18 34, 82 34, 86 34, 77 35, 56 36, 18

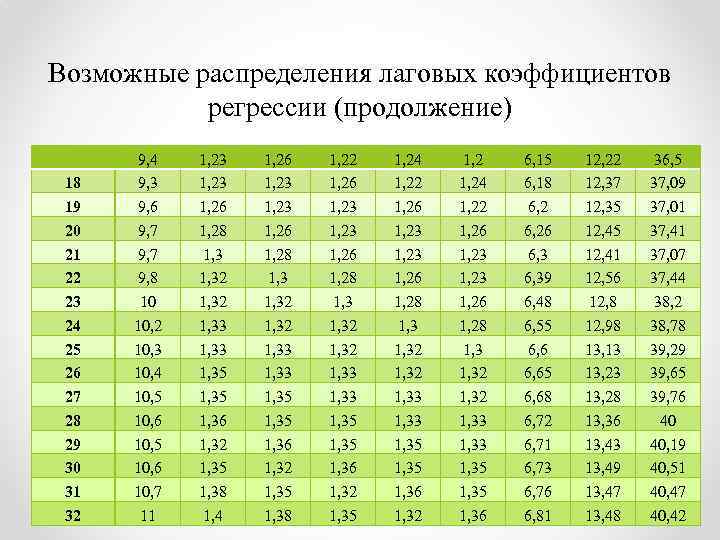Возможные распределения лаговых коэффициентов регрессии (продолжение) 18 19 20 21 22 23 24 25 Возможные распределения лаговых коэффициентов регрессии (продолжение) 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 9, 4 9, 3 9, 6 9, 7 9, 8 10 10, 2 10, 3 10, 4 10, 5 10, 6 10, 7 11 1, 23 1, 26 1, 28 1, 32 1, 33 1, 35 1, 36 1, 32 1, 35 1, 38 1, 4 1, 26 1, 23 1, 26 1, 28 1, 32 1, 33 1, 35 1, 36 1, 32 1, 35 1, 38 1, 22 1, 26 1, 23 1, 26 1, 28 1, 32 1, 33 1, 35 1, 36 1, 32 1, 35 1, 24 1, 22 1, 26 1, 23 1, 26 1, 28 1, 32 1, 33 1, 35 1, 36 1, 32 1, 24 1, 22 1, 26 1, 23 1, 26 1, 28 1, 32 1, 33 1, 35 1, 36 6, 15 6, 18 6, 26 6, 39 6, 48 6, 55 6, 65 6, 68 6, 72 6, 71 6, 73 6, 76 6, 81 12, 22 12, 37 12, 35 12, 41 12, 56 12, 8 12, 98 13, 13 13, 28 13, 36 13, 43 13, 49 13, 47 13, 48 36, 5 37, 09 37, 01 37, 41 37, 07 37, 44 38, 2 38, 78 39, 29 39, 65 39, 76 40 40, 19 40, 51 40, 47 40, 42

bₒ=cₒ b₁=cₒ+c₁+c₂ b₂=cₒ+2 c₁+4 c₂ b₃=cₒ+3 c₁+9 c₂ b₄=cₒ+4 c₁+16 c₂ Соответственно модель bₒ=cₒ b₁=cₒ+c₁+c₂ b₂=cₒ+2 c₁+4 c₂ b₃=cₒ+3 c₁+9 c₂ b₄=cₒ+4 c₁+16 c₂ Соответственно модель с распределенными лагами примет вид: yt= a+cₒ ɀₒ+c₁ ɀ₁+c₂ ɀ₂+ ﻉ t

Расчет преобразованных переменных ɀj представлен в таблице, где: • • ɀₒ=хt+xt-1+xt-2+xt-3+xt-4 • ɀ₁= xt-1+2 Расчет преобразованных переменных ɀj представлен в таблице, где: • • ɀₒ=хt+xt-1+xt-2+xt-3+xt-4 • ɀ₁= xt-1+2 xt-2+3 xt-3+4 xt-4 • ɀ₂= xt-1+4 xt-2+9 xt-3+16 xt-4 уt=-4, 7115+3, 7713ɀₒ 2, 2668ɀ₁+0, 5065ɀ₂+ ﻉ t t -15, 0 5, 8 -2, 6 2, 6

Найдем коэффициенты регрессии исходной модели, т. е. bj, используя выражения bj через коэффициенты cₒ, Найдем коэффициенты регрессии исходной модели, т. е. bj, используя выражения bj через коэффициенты cₒ, c₁ и c₂ •

• •

• •

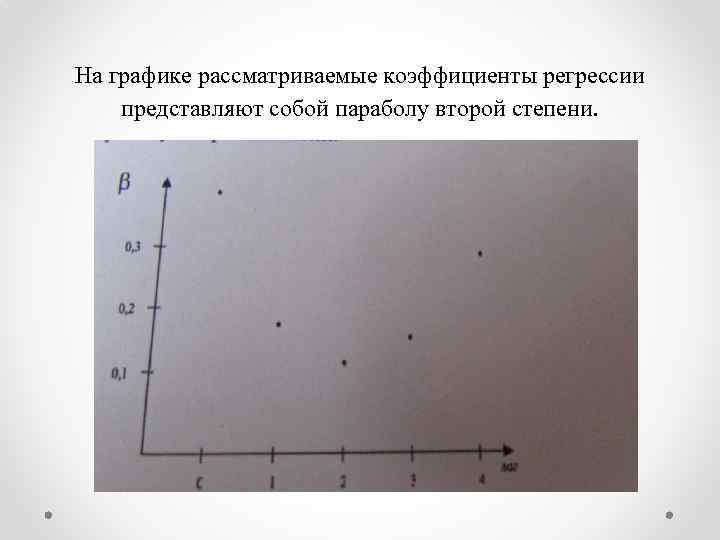На графике рассматриваемые коэффициенты регрессии представляют собой параболу второй степени. На графике рассматриваемые коэффициенты регрессии представляют собой параболу второй степени.

Если к исходным данным нашего примера применить традиционный МНК, то результаты окажутся следующими: • Если к исходным данным нашего примера применить традиционный МНК, то результаты окажутся следующими: •