ТЕМА КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ План 1 Виды

ТЕМА. КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ План 1. Виды и формы связей. Понятие о корреляционной связи. 2. Корреляционный метод анализа взаимосвязи. 3. Регрессионный метод анализа взаимосвязи. Построение однофакторной модели связи. 4. Проверка адекватности регрессионной модели. 5. Непараметрические методы.

1. Виды и формы связей. Понятие о корреляционной связи. Важнейшей задачей статистики является исследование существующих связей между явлениями. В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями. Причинно-следственные отношения – это такая связь явлений и процессов, когда изменение одного из них (причины) ведет к изменению другого (следствия). Социально-экономические явления представляют собой результат одновременного воздействия большого числа причин. Поэтому при проведении статистического исследования необходимо выявить факторы (признаки), которые оказывают основное влияние на вариацию изучаемых явлений и процессов.

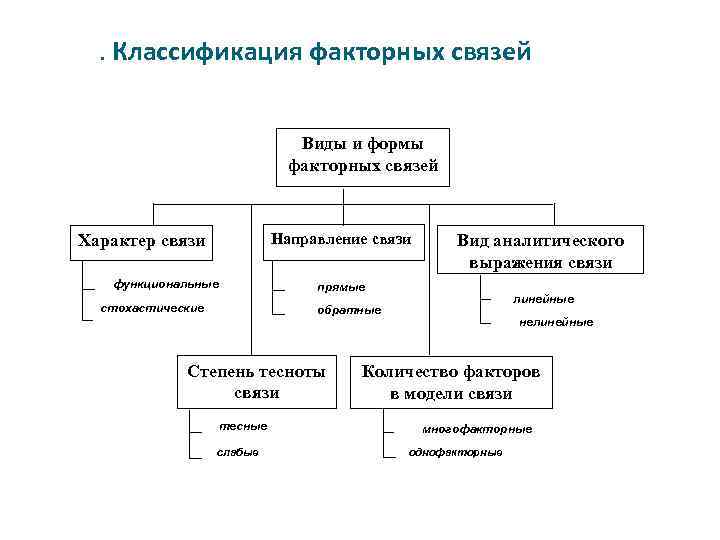. Классификация факторных связей Виды и формы факторных связей Направление связи Характер связи функциональные Вид аналитического выражения связи прямые стохастические линейные обратные Степень тесноты связи тесные слабые нелинейные Количество факторов в модели связи многофакторные однофакторные

Функциональные связи Связь результативного признака Y с факторным признаком X называется функциональной, если каждому возможному значению xi признака X соответствует одно (или несколько) однозначно определенных значений yi признака Y. Математической моделью однофакторной функциональной связи служит уравнение yi=f(xi). В случае зависимости признака Y от нескольких факторных признаков X 1, X 2, … , Xm модель связи имеет вид:

Особенность функциональной связи Характерная особенность функциональной связи состоит в том, что проявляется в каждом отдельном случае наблюдения и для каждой единицы исследуемой совокупности. При этом известен полный перечень всех факторов, влияющих на результативный признак Y, а также точный механизм их влияния, выраженный формулой функции f(х). Ввиду этого функциональные связи характеризуются как полные, жесткие, детерминированные, строго определенные.

Стохастические связи В области социально-экономических явлений факторные связи редко носят жестко детерминированный характер. Это объясняется тем, что наряду с существенными факторами, оказывающими основное, главное влияние на величину результативного признака, на него воздействуют и многие другие, в том числе случайные факторы, причем механизм влияния всех факторов в совокупности точно определить невозможно. Расходы семьи на продукты питания во многом зависят от семейных доходов, но нельзя сказать, что с ростом дохода X на определенную величину ∆х расходы семьи на питание Y изменятся на строго определенную величину ∆y, поскольку на Y влияют и многие другие факторы - размер и состав семьи, цены на продукты питания, насыщенность рынка товарами, потребительские привычки семьи и т. д.

Одному и тому же доходу xi будут соответствовать различные по величине расходы на питание yi 1, yi 2, … , yik, причем появление каждого конкретного значения yi носит случайный характер. Связи, учитывающие случайный характер зависимости признаков, относят к числу стохастических (вероятностных). Стохастическая связь признаков – это связь, при которой одному и тому же значению хi фактора X (случайному или неслучайному) могут соответствовать различные случайные значения yi 1, yi 2, … , yik результативного признака Y:

Возможность появления для одного и того же значения хi различных результативных значений yi 1, yi 2, … , yik обусловлено тем, что на признак Y, помимо учтенного фактора Х, одновременно воздействуют многие другие неучтенные факторы, а также случайные факторы, которые в каждом конкретном наблюдении могут менять и силу, и направление своего воздействия. Ввиду всех этих обстоятельств значения результативного признака Y, отвечающие факторному значению хi, оказываются подверженными случайному разбросу yi 1, yi 2, … , yik, причем появление того или иного значения yi (в силу его случайного характера) не может быть определено точно, а лишь предсказано с некоторой вероятностью.

Математическая модель однофакторной стохастической связи имеет вид уравнения где xi, yi – значения факторного и результативного признаков соответственно, - функция, определяющая ту часть значения признака yi, которая формируется под воздействием учтенного в модели фактора X; - часть значения признака yi, которая возникает вследствие действия неучтенных или случайных факторов, а также возможных ошибок измерения признаков Х, Y. Если в модели учитывается зависимость признака Y от ряда факторов, то модель имеет вид

Особенность стохастической связи Характерной особенностью стохастических связей является то, что они обнаруживаются не в каждом отдельном случае наблюдения, как при функциональных связях, а лишь при достаточно большом числе наблюдений. При стохастических связях не известен ни полный перечень факторных признаков, ни точное правило их взаимодействия с результативным признаком Y, поэтому эти связи характеризуются как неполные, нежесткие, случайные, недетерминированные, неопределенные.

Неполнота корреляционных связей -подмножество факторов, степень влияния которых попадает в поле зрения исследования -подмножество факторов, влияние которых на результат остается неучтенным

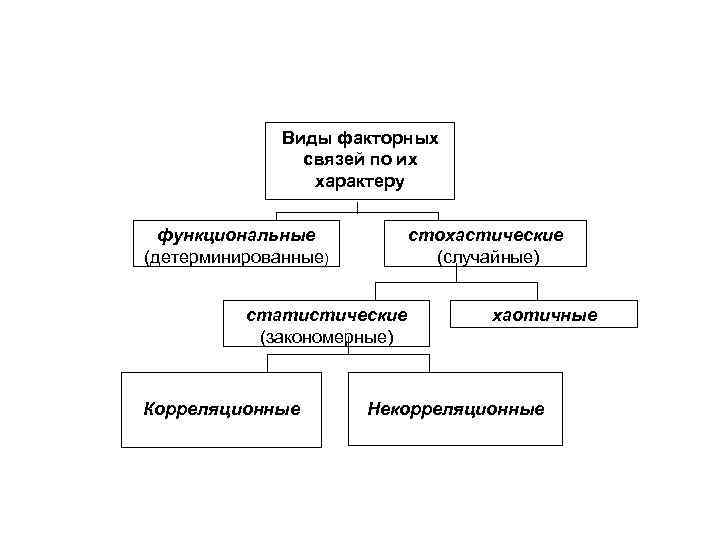Классификация факторных связей по их характеру Виды факторных связей по их характеру функциональные (детерминированные) стохастические (случайные) статистические (закономерные) Корреляционные хаотичные Некорреляционные

Корреляционные связи, их свойства и формы выражения Стохастическую связь между случайными значениями признаков X и Y называют статистической, если с изменением значений хi фактора Х закономерным образом изменяется какой-либо из обобщающих статистических показателей распределения yi 1 , yi 2, … , yi признака Y. Если при изменении xi имеет место закономерное изменение средних арифметических значений распределения признака Y, то статистическая связь называется корреляционной.

Теснота корреляционной связи характеризует степень ее приближения к функциональной связи. В зависимости от направления изменения результативного признака различаются прямые и обратные связи. Если результативный признак Y изменяется в том же направлении, что и факторный признак Х, то связь прямая. Если же результативный признак меняется в противоположном направлении, то связь обратная. По количеству факторов, действующих на результативный признак, различают связи однофакторные и многофакторные. Если исследуется связь между одним признаком-фактором Х и результативным признаком Y, то говорят об однофакторной связи и парной корреляции Если же изучается воздействие на Y нескольких факторных признаков X 1, X 2, … , Xm, то связь называют многофакторной, а корреляцию множественной.

2. Корреляционный метод анализа взаимосвязи Корреляционный метод анализа - решаются две основные задачи. 1. Установление факта наличия корреляционной связи. 2. Измерение тесноты корреляционной связи по фактическим, т. е. эмпирическим данным. Для решения первой задачи - установления наличия корреляционной связи, используется ряд методов: • приведения параллельных рядов; • графический; • корреляционных таблиц: • аналитических группировок.

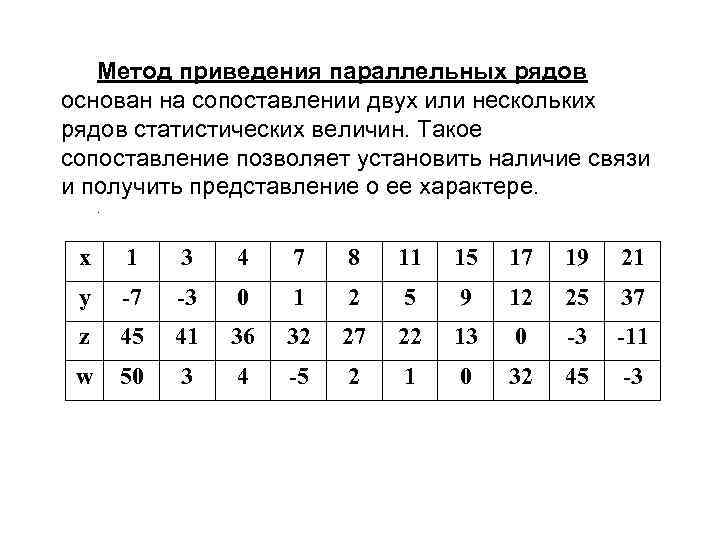Метод приведения параллельных рядов основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере. . x 1 3 4 7 8 11 15 17 19 21 y -7 -3 0 1 2 5 9 12 25 37 z 45 41 36 32 27 22 13 0 -3 -11 w 50 3 4 -5 2 1 0 32 45 -3

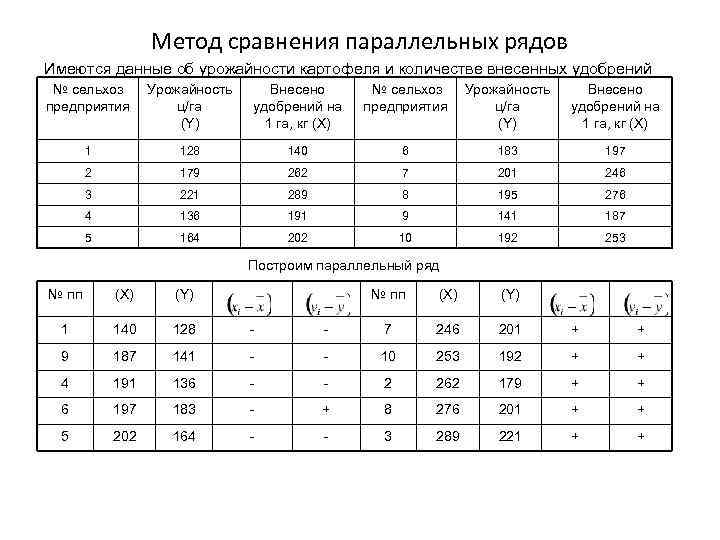Метод сравнения параллельных рядов Имеются данные об урожайности картофеля и количестве внесенных удобрений № сельхоз предприятия Урожайность ц/га (Y) Внесено удобрений на 1 га, кг (Х) 1 128 140 6 183 197 2 179 262 7 201 246 3 221 289 8 195 276 4 136 191 9 141 187 5 164 202 10 192 253 Построим параллельный ряд № пп (Х) (Y) 1 140 128 - - 7 246 201 + + 9 187 141 - - 10 253 192 + + 4 191 136 - - 2 262 179 + + 6 197 183 - + 8 276 201 + + 5 202 164 - - 3 289 221 + +

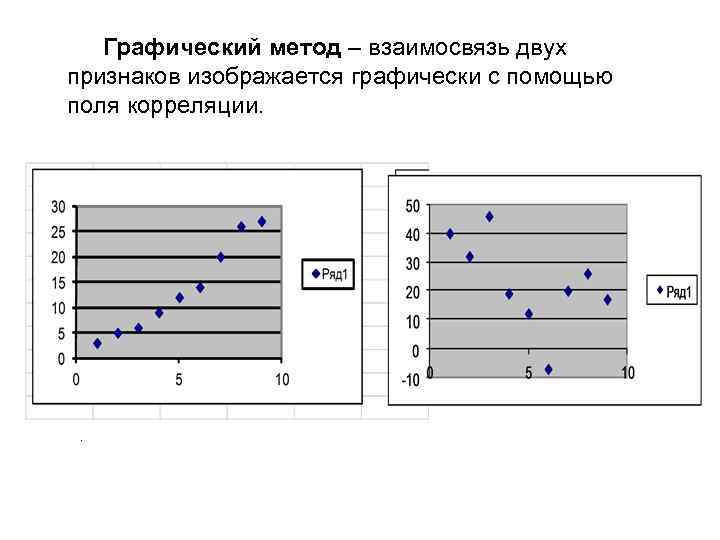Графический метод – взаимосвязь двух признаков изображается графически с помощью поля корреляции. .

Метод корреляционных таблиц. Корреляционная таблица – это специальная комбинационная таблица, в которой представлена группировка по двум взаимосвязанным признакам: факторному и результативному. В корреляционной таблице строки соответствуют группировке факторных значений х , i столбцы – группировке результативных значений yi. На пересечении j-ой строки и k-ого столбца указывается численность единиц совокупности, факторные значения которых принадлежат j-му интервалу группировки признака Х, а результативные - k-му интервалу группировки признака Y. Концентрация частот около диагоналей матрицы данных свидетельствует о наличии корреляционной связи между признаками.

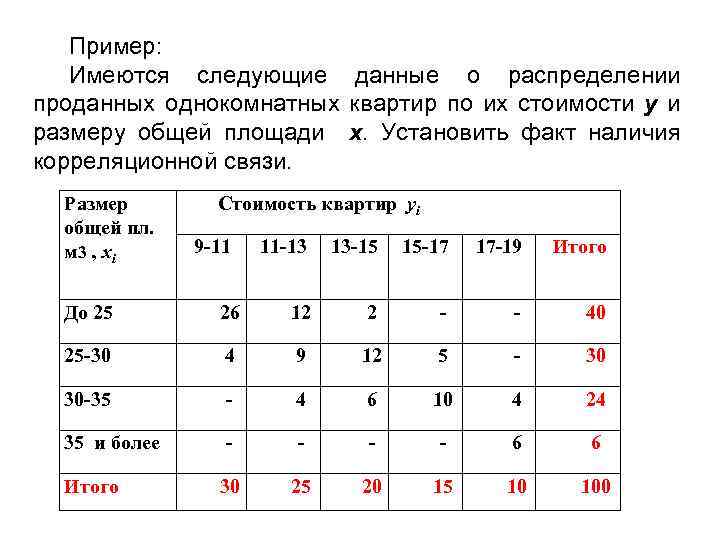Пример: Имеются следующие данные о распределении проданных однокомнатных квартир по их стоимости у и размеру общей площади х. Установить факт наличия корреляционной связи. Размер общей пл. м 3 , xi Стоимость квартир уi 9 -11 11 -13 13 -15 15 -17 17 -19 Итого До 25 26 12 2 - - 40 25 -30 4 9 12 5 - 30 30 -35 - 4 6 10 4 24 35 и более - - 6 6 30 25 20 15 10 100 Итого

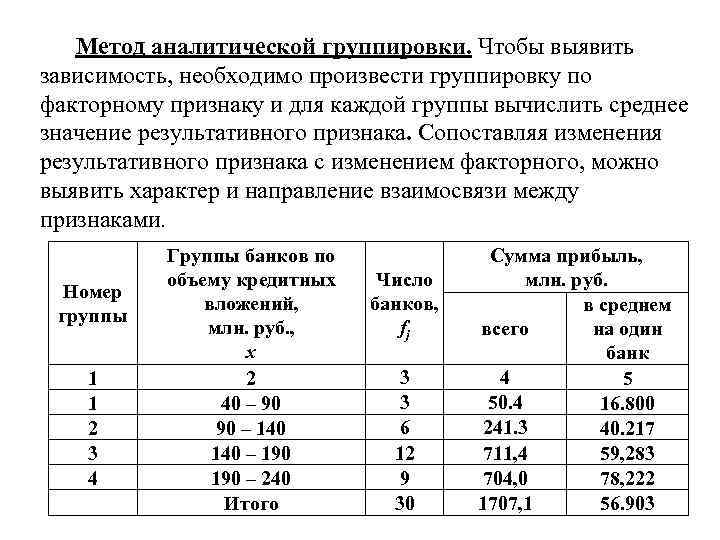Метод аналитической группировки. Чтобы выявить зависимость, необходимо произвести группировку по факторному признаку и для каждой группы вычислить среднее значение результативного признака. Сопоставляя изменения результативного признака с изменением факторного, можно выявить характер и направление взаимосвязи между признаками. Номер группы 1 1 2 3 4 Группы банков по объему кредитных вложений, млн. руб. , х 2 40 – 90 90 – 140 – 190 – 240 Итого Число банков, fj 3 3 6 12 9 30 Сумма прибыль, млн. руб. в среднем всего на один банк 4 5 50. 4 16. 800 241. 3 40. 217 711, 4 59, 283 704, 0 78, 222 1707, 1 56. 903

Для решения второй задачи корреляционного метода анализа – измерения тесноты связи используются специальные коэффициенты, которые выражают тесноту связи количественными величинами: 1. - эмпирический коэффициент детерминации (причинности), определяющий силу связи, т. е. оценивающий, насколько вариация результативного признака Y объясняется вариацией фактора Х. 2. - эмпирическое корреляционное отношение, выступающее как универсальный показатель тесноты связи при любой форме связи (как линейной, так и нелинейной);

3. r - линейный коэффициент корреляции, измеряющий тесноту связи в предположении линейности взаимосвязи признаков Х и Y; где σx и σy – среднеквадратическое отклонение факторного и результативного признаков

4. R 2 - индекс детерминации (называемый также теоретическим коэффициентом детерминации и обозначаемый ), показывающий, какая часть общей вариации расчетных (теоретических) значений признака Y объясняется вариацией фактора X; 5. R – индекс корреляции (называемый также теоретическим корреляционным отношением и обозначаемый ), оценивающий степень тесноты связи между факторными значениями xi и расчетными результативными значениями

3. Регрессионный метод анализа взаимосвязи. Построение однофакторной модели связи Метод регрессионного анализа заключается в определении аналитического выражения связи. Уравнение регрессии, или статистическая модель связи социально-экономических явлений, выражается функцией -для однофакторной модели - для многофакторной модели. Одной из проблем построения уравнений регрессии является определение числа факторных признаков, которые включаются в модель. Их число должно быть оптимальным.

Типы функций, используемых для построения уравнения регрессии - прямая - парабола 2 -го порядка - гипербола - показательная функция и др.

Параметры уравнения регрессии а 0, а 1, а 2, … находят методом наименьших квадратов. Сущность метода заключается в нахождении параметров а 0, а 1, а 2, …, при которых минимизируется сумма квадратов отклонений фактических значений результативного признака от теоретических, полученных по выбранному уравнению регрессии: Для линейной зависимости Рассматривая S как функцию параметров а 0 и а 1, найдем частные производные по а 0 и а 1 и результат приравняем нулю, так как ищем min.

В линейном уравнении регрессии параметр а 1 – называется коэффициентом регрессии. Он показывает на сколько измениться в среднем значение результирующего признака Y при увеличении факторного признака Х на единицу собственного измерения. А параметр а 0 показывает усредненное влияние на результирующий признак всех неучтенных факторов.

Парная линейная регрессия Система нормальных уравнений Для несгруппированных данных Для сгруппированных данных Если оба уравнения разделить на n, система примет вид: отсюда или с применение линейного коэффициента корреляции Тогда уравнение связи примет вид:

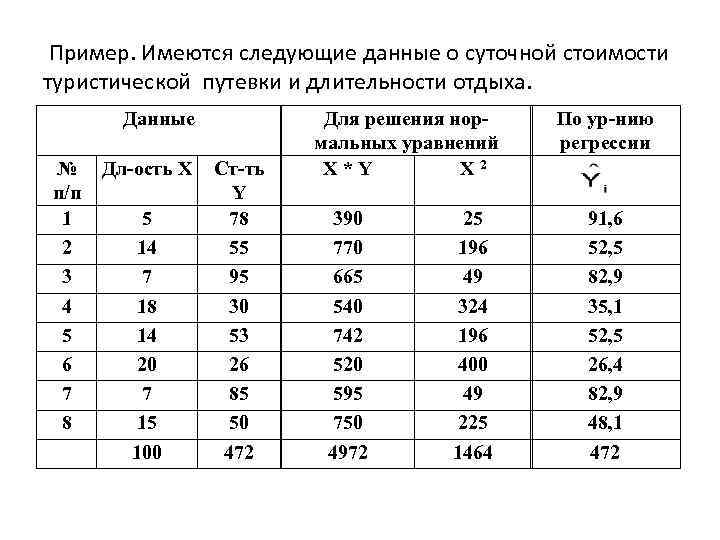Пример. Имеются следующие данные о суточной стоимости туристической путевки и длительности отдыха. Данные № п/п 1 2 3 4 5 6 7 8 Дл-ость Х 5 14 7 18 14 20 7 15 100 Ст-ть Y 78 55 95 30 53 26 85 50 472 Для решения нормальных уравнений X * Y X 2 390 770 665 540 742 520 595 750 4972 25 196 49 324 196 400 49 225 1464 По ур-нию регрессии 91, 6 52, 5 82, 9 35, 1 52, 5 26, 4 82, 9 48, 1 472

Система нормальных уравнений для данного примера в случае линейной связи имеет вид: Коэффициент эластичности показывает среднее изменение результативного признака при изменении факторного признака на 1%.

4. Проверка адекватности регрессионной модели – это проверка соответствия модели фактическим статистическим данным. Корреляционный и регрессионный анализ обычно проводится для небольшой по объему совокупности. Поэтому показатели регрессии и корреляции могут быть искажены действием случайных факторов. Чтобы проверить насколько эти показатели характерны для всей генеральной совокупности, необходимо проверить адекватность построенных статистических моделей.

1) Проверка значимости каждого коэффициента регрессии. Для этого осуществляется проверка каждого коэффициента регрессии. на. Для простой линейной регрессии проверка осуществляется с помощью t–критерия Стьюдента. При этом вычисляют фактические значения t–критерия: где n - объем выборки; - среднее квадратическое отклонение результативного признака yi от выравненных значений ; - среднее квадратическое отклонение факторного признака от общей средней.

2) Определение практической пригодности построенной регрессионной модели. Практическую пригодность построенной модели можно охарактеризовать по величине линейного коэффициента корреляции r: - близость к единице свидетельствует о хорошей аппроксимации исходных (фактических) данных с помощью построенной линейной функции связи; - близость к нулю означает, что связь между фактическими данными Х и Y нельзя аппроксимировать как построенной, так и любой другой линейной моделью. Пригодность построенной регрессионной модели для практического использования можно оценить и по величине индекса детерминации R 2, показывающего, какая часть общей вариации признака Y объясняется в построенной модели вариацией фактора X.

5. Непараметрические методы a b a+b c d c+d a+c b+d Применительно к этой таблице с частотами a, b, c, d коэффициент ассоциации: -1 ≤ k ≤ 1 Чем ближе |k| к 1, тем сильнее связаны между собой изучаемые признаки. При |k|>0, 3 – наличие связи.

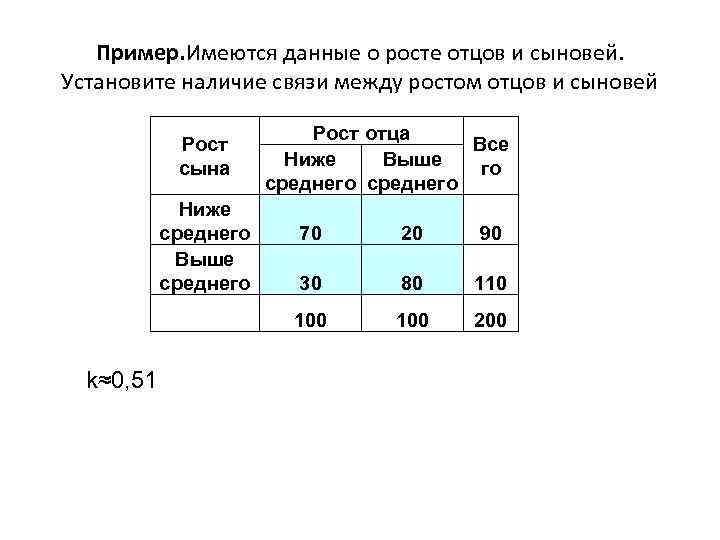Пример. Имеются данные о росте отцов и сыновей. Установите наличие связи между ростом отцов и сыновей Рост сына Ниже среднего Выше среднего k≈0, 51 Рост отца Все Ниже Выше го среднего 70 20 90 30 80 110 100 200

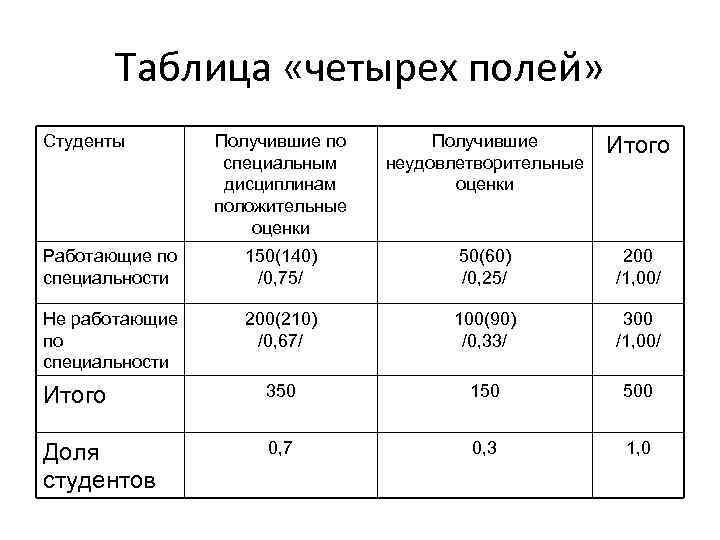Таблица «четырех полей» Студенты Получившие по специальным дисциплинам положительные оценки Получившие неудовлетворительные оценки Итого Работающие по специальности 150(140) /0, 75/ 50(60) /0, 25/ 200 /1, 00/ Не работающие по специальности 200(210) /0, 67/ 100(90) /0, 33/ 300 /1, 00/ Итого 350 150 500 Доля студентов 0, 7 0, 3 1, 0

Показатели тесноты связи атрибутивных признаков а b a+b c d c+d a+c b+d a+b+c+d Коэффициент ассоциации Коэффициент контингенции