Тема исследования Исследование проблемы решения квадратных уравнений Автор

Тема исследования Исследование проблемы решения квадратных уравнений Автор: Рыбалка Иван Руководитель: Васильченко В. Д. МКОУ Бутурлиновская СОШ № 7

расширение и углубление знаний по решению квадратных уравнений Для достижения цели я поставил перед собой следующие задачи 1. Изучить литературу по выбранной теме; 2. Изучить историю возникновения и решения квадратных уравнений; 3. Изучить способы решения квадратных уравнений разного вида

1)Изучить историю развития квадратного уравнения. 2)Рассмотреть какие способы решений уравнений есть 3)Выбор оптимальных способов для себя

О квадратных уравнениях до ал. Хорезми Потребности жизни, главным образом земледелия и астрономии, ставили ученых древности перед необходимостью уметь решать уравнения как квадратные, так и более высоких степеней. Решение некоторых видов численных квадратных уравнений было известно еще вавилонянам примерно за полторы тысячи лет до нашей эры. В более поздние времена греки, а за ними индийцы научились решать графически некоторые виды квадратных уравнений. Однако общих методов для всех видов квадратных уравнений у них не было

Находки древности Методы решения квадратных уравнений были известны ещё в давние времена. Их умели решать вавилоняне ( около 2 тыс. лет до н. э. ). Об этом свидетельствуют найденные клинописные тексты задач с решениями в виде уравнений. Также они излагались в вавилонских рукописях царя Хаммурапи.

Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших до наших дней выводов этой формулы принадлежит индийскому математику Брахмагупте (около 598 г. ). Вот одна из задач знаменитого индийского математика XII в Бхаскары: «Обезьянок резвых стая Всласть поевши, развлекалась, Их в квадрате часть восьмая На поляне забавлялась. А двенадцать по лианам… Стали прыгать, повисая… Сколько ж было обезьянок, Ты скажи мне, в этой стае? »

Находки древности Задача Диофанта Найти два числа, зная, что их сумма равна 20, а произведение – 96» Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, т. к. если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10+х, другое же меньше, т. е. 10 х. Разность между ними 2 х. Отсюда уравнение(10+х)(10 х)=96 или же 100 -х 2=96 , х2 -4=0 Отсюда х=2. Одно из искомых чисел равно 12, другое 8. Решение х=-2 для Диофанта не существует, т. к. греческая математика знала только положительные числа.

Находки древности Квадратные уравнения в Европе XIII-XVII вв. Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абака» , написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Книга способствовала распространению алгебраических знаний в Италии, в Германии, Франции и др. странах Европы.

Общий вид квадратного уравнения

Общий вид квадратного уравнения B -четное

Неполные квадратные уравнения

Квадратное уравнение имеет всегда два корня! корни могут быть иногда равными, иногда мнимыми! Имеет место запись, например : х=2; х=2

Теорема Виета Знаменитый французский учёный Франсуа Виет(1540 -1603) Сумма корней приведенного квадратного уравнения х2+ рх + q = 0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену, т. е. х1 + х2 = - р, х 1 · х2 = q. Теорема, обратная теореме Виета. Если р, q, x 1, x 2 таковы, что х1 + х2 = - р, х1 · х2 = q, то х1 и х2 – корни уравнения х2+ рх + q = 0

Решение уравнений способом «переброски» . Рассмотрим квадратное уравнение ах2 + bх + с = 0, где а ≠ 0. Умножая обе его части на а, получаем уравнениеа 2 х2 + аbх + ас = 0. Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у2 + by + ас = 0, равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = у1/а и х1 = у2/а. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски» . Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат. • Пример. Решим уравнение 2 х2 – 11 х + 15 = 0. Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим у2 – 11 у + 30 = 0. Согласно теореме Виета у1 = 5 х1 = 5/2 x 1 = 2, 5 у2 = 6 x 2 = 6/2 x 2 = 3.

Свойства коэффициентов квадратного уравнения. ах2 + bх + с = 0, где а ≠ 0. 1) Если, а+ b + с = 0 (т. е. сумма коэффициентов равна нулю), то х1 = 1, х2 = с/а. Пример. Решим уравнение 132 х2 – 247 х + 115 = 0. Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то х1 = 1, х2 = c/a = 115/132. Ответ: 1; 115/132. 2)Если a + c=b , то х1 =-1, х2 = -с/а Решим уравнение 2 х2 + 3 х +1= 0 2 - 3+1=0, значит х1= - 1, х2 = -1/2 Ответ: х1=-1, х2 =-1/2

Графическое решение квадратного уравнения Если в уравнении х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = px - q. Построим графики зависимости у = х2 и у = - px - q. График первой зависимости - парабола, проходящая через начало координат. График второй зависимости - прямая (рис. 1). Возможны следующие случаи: - прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения; - прямая и парабола могут касаться (одна общая точка), т. е. уравнение имеет одно решение; - прямая и парабола не имеют общих точек, т. е. квадратное уравнение не имеет корней.

Разложение левой части уравнения на множители. х2 - 2 х - 8 = 0. Разложим левую часть на множители: х2 - 2 х - 8 = х2 - 4 х +2 х -8 = х(х -4 ) + 2(х -4) = (х + 2)(х -42). (х + 2)(х -4)=0. Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = -2, а также при х = 4. Это означает, что число - 2 и 4 являются корнями уравнения х2 - 2 х - 8 = 0.

Метод выделения полного квадрата.

Решение квадратных уравнений с помощью циркуля и линейки.

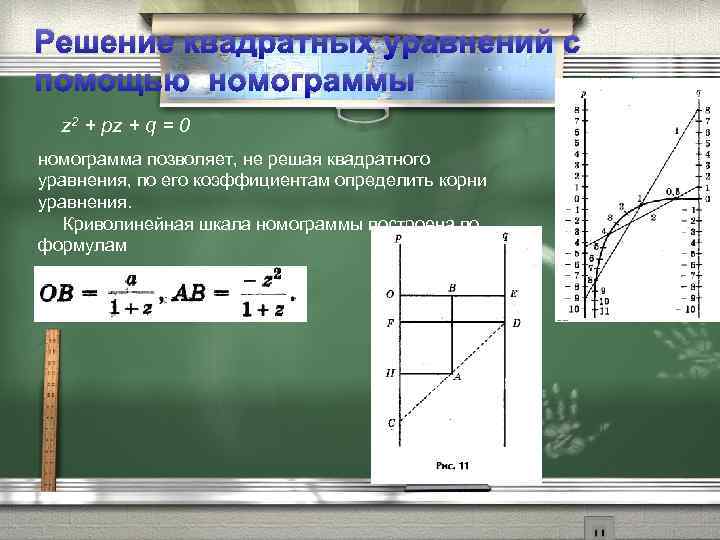
Решение квадратных уравнений с помощью номограммы z 2 + pz + q = 0 номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения. Криволинейная шкала номограммы построена по формулам

Геометрический способ решения квадратных уравнений «Квадрат и десять корней равны 39» х2 + 10 х = 39. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2, 5, следовательно, площадь каждого равна 2, 5 х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2, 5, а площадь 6, 25. Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников (4 • 2, 5 х = 10 х ) и четырех пристроенных квадратов (6, 25 • 4 = 25), т. е. S = х2 + 10 х + 25. Заменяя х2 + 10 х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т. е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим

Способ решения квадратных уравнений по теореме Безу При делении P(х) на х - в остатке может получиться лишь некоторое число r (если r = 0, то деление выполняется без остатка): P(x) = (x - ) Q (x) + r. х²-4 х+3=0 Р 2(х)= х²-4 х+3 α; ± 1, ± 3. α =1, 1 -4+3=0 Разделим р(х) на (х-1) (х²-4 х+3)/(х-1)=х-3 х²-4 х+3=(х-1)(х-3)=0 Х-1=0; или х-3=0, ; . х=1, х=3 Ответ: х1=2, х2=3

При выполнении работы были замечено: Способы которыми буду пользоваться: 1. 2. 3. 4. 5. Теорема Виета По дискриминанту Свойства коэффициентов(2) Метод «переброски» Графический способ Способы интересные, но занимают много времени и не всегда удобны. 1. 2. 3. 4. 5. С помощью номограммы Линейки и циркуля Выделение полного квадрата Разложение левой части на множители По т. Безу Преклоняюсь перед учеными которые открыли эти способы и дали науке толчок для развития в теме «Решение квадратных уравнений»

квадратные уравнения играют огромную роль в развитии математики. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза. Эти знания могут пригодиться нам на протяжении всей жизни. Так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должно заинтересовать увлекающихся математикой учеников.

1)Математика. Алгебра. Функции. Анализ данных. 8 класс: Учебник для общеобразовательных учреждений / Г. В. Дорофеев и др. – М. : Дрофа, 2004 2)Гусев В. А. , Мордкович А. Г. Математика: Справочные материалы: Книга для учащихся. – М. : Просвещение, 1988 3)Глейзер Г. И. , История математики в школе. – М. : просвещение, 1982 4)Брадис В. М. Четырехзначные математические таблицы для среденй школы. – м. , просвещение, 1990 5)Окунев А. К. , Квадратичные функции, уравнения и неравенства. Пособие для учителя. – М. : Просвещение, 1972 6)Пресман А. А. Решение квадратного уравнения с помощью циркуля и линейки. М. , Квант, № 4/72. С. 34. 7)Дидактические материалы по алгебре. 1)www. textreferat. com 2)www. portfolio. ru