Тема Исследование функции с помощью производной Точки экстремума

Тема: Исследование функции с помощью производной. Точки экстремума функции и их отыскание. § 35, п. 2, стр. 174.

Исследование функции на монотонность и точки экстремума. Стр. 179 Алгоритм 1. 2. 3. 4. 1. f΄(х)= 2. Стационарные точки: …f΄(х)=0 3. Отметить точки на числовой прямой, определить знаки производной на промежутках. 4. по теореме 1, 2, 3 определить возрастание и убывание функции.

Задание: 1. Найти угловой коэффициент касательной к=? ; 2. Составить уравнение касательной к графику функции в точке а. 3. Исследовать на монотонность и точки экстремума. 1) у=4 х³+4, а=5

Задание: 1. Найти угловой коэффициент касательной к=? ; 2. Составить уравнение касательной к графику функции в точке а. 3. Исследовать на монотонность и точки экстремума. 2) у=2 х²+12 х-1, а=2 3) у=-4 х³-12 х+3, а=-1 4) у=-х³-2 х+5, а=-3 5) у=х²-х+3, а=0

2) у=2 х²+12 х-1, Решение. а=2

2) у=2 х²+12 х-1, Решение. а=2

3) у=-4 х³-12 х+3, Решение. а=-1

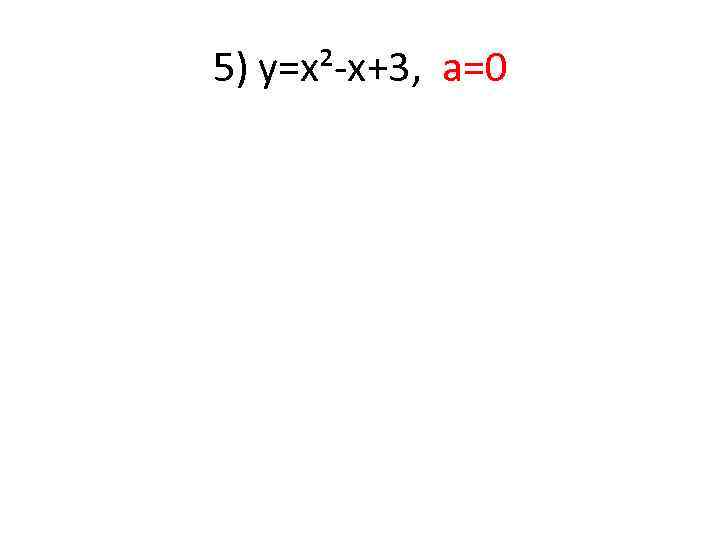5) у=х²-х+3, а=0

Эталон ответа: 1) 2) 3) 4) 5) к=300, к=20, к=-24, к=-11, к=-1, у=300 х-996 у=-9+20 х у=-5 -24 х у=-49 -29 х у=6 -х

Домашнее задание.