Тема Алгоритмы и структуры данных продолжение Лекция 28

Тема Алгоритмы и структуры данных (продолжение) Лекция 28. 10. 13 г. 1

Структура данных «пирамида» (binary heap - «двоичная куча» ) Пирамида — это структура данных, представляющая собой объект-массив, который можно рассматривать как «почти полное бинарное дерево» . Каждый узел этого дерева соответствует определенному элементу массива. На всех уровнях, кроме, может быть, последнего, дерево полностью заполнено (заполненный уровень — это такой, который содержит максимально возможное количество узлов). Последний (нижний) уровень заполняется слева направо до тех пор, пока в массиве не закончатся элементы. 0 1 3 7 2 2 14 4 8 8 4 16 9 7 5 9 10 16 14 10 8 6 7 9 3 2 4 1 3 1 Будем называть элементы массива с индексами i*2+1 и i*2+2 потомками элемента с индексом i, а элемент i будет называться предком этих элементов. Несложно заметить, что потомки двух разных элементов не пересекаются, и каждый элемент, кроме нулевого, является чьим-либо потомком. Лекция 28. 10. 13 г. 2

Структура данных «пирамида» Различают два вида пирамид: неубывающие (максимальные) и невозрастающие (минимальные). В пирамидах обоих видов значения, расположенные в узлах, удовлетворяют основному свойству пирамиды: • для неубывающих пирамид: «каждый элемент не меньше своих потомков» ; • для невозрастающих пирамид: «каждый элемент не больше своих потомков» . Следствием этого основного свойства пирамиды является утверждение: • для неубывающих пирамид: «максимальный элемент находится в корне дерева (занимает первое место в массиве)» ; • для невозрастающих пирамид: «минимальный элемент находится в корне дерева (занимает первое место в массиве)» . В дальнейшем для определенности под «пирамидой» будем подразумевать максимальную пирамиду. Лекция 28. 10. 13 г. 3

Реализация пирамиды с помощью вектора Как будет указано далее, пирамида является динамической структурой данных, поэтому её целесообразно реализовывать на базе ранее сконструированной структуры данных «вектор» , а не на базе обычного массива. Заметим, что в отличие от стека и очереди, пирамида не требует никаких дополнительных элементов, кроме тех, что есть у вектора, поэтому структура данных «пирамида» (Heap) является просто оболочкой над структурой данных Vector: typedef struct Heap {Vector v; } Heap; В этих условиях функция инициализации пирамиды – init_h будет тривиальной: void init_h(Heap *hp) { init(&hp->v); } Функция получения максимального элемента Heap_Maximum также тривиальна, т. к. максимальный элемент всегда находится в начале массива: int Heap_Maximum(Heap *hp, double *z) { if(hp->v. sz == 0) return 0; // если пирамида пуста *z = hp->v. elem[0]; return 1; } Лекция 28. 10. 13 г. 4

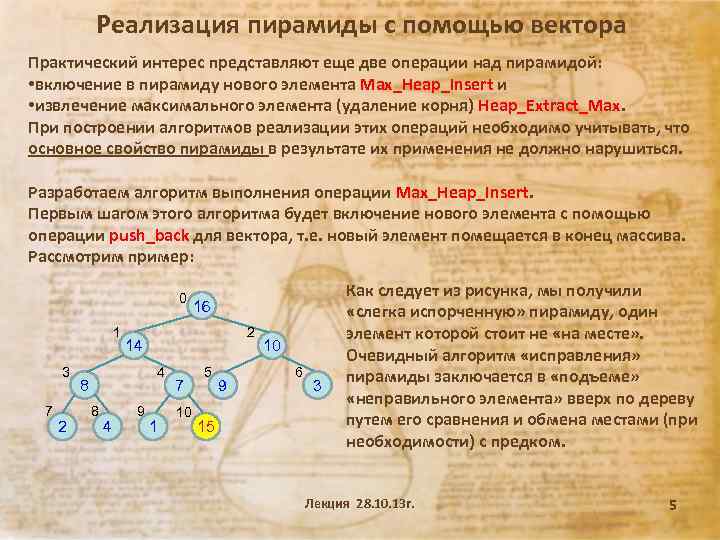Реализация пирамиды с помощью вектора Практический интерес представляют еще две операции над пирамидой: • включение в пирамиду нового элемента Max_Heap_Insert и • извлечение максимального элемента (удаление корня) Heap_Extract_Max. При построении алгоритмов реализации этих операций необходимо учитывать, что основное свойство пирамиды в результате их применения не должно нарушиться. Разработаем алгоритм выполнения операции Max_Heap_Insert. Первым шагом этого алгоритма будет включение нового элемента с помощью операции push_back для вектора, т. е. новый элемент помещается в конец массива. Рассмотрим пример: 0 1 3 7 2 2 14 4 8 8 4 16 9 1 7 10 5 15 9 10 6 3 Как следует из рисунка, мы получили «слегка испорченную» пирамиду, один элемент которой стоит не «на месте» . Очевидный алгоритм «исправления» пирамиды заключается в «подъеме» «неправильного элемента» вверх по дереву путем его сравнения и обмена местами (при необходимости) с предком. Лекция 28. 10. 13 г. 5

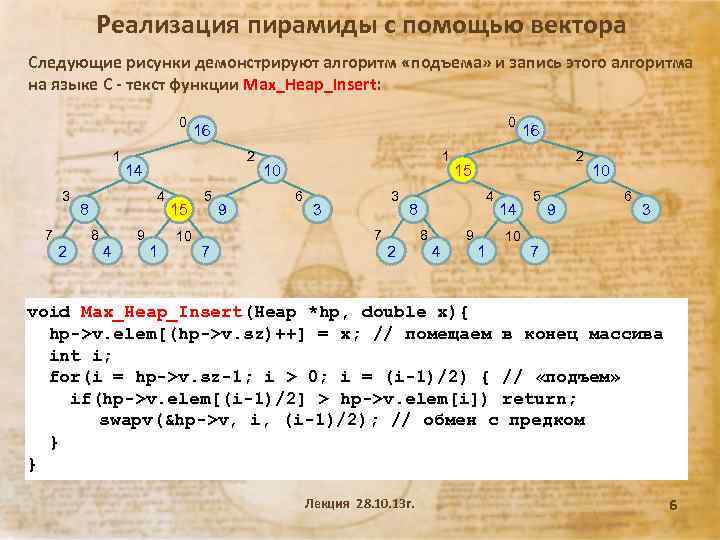Реализация пирамиды с помощью вектора Следующие рисунки демонстрируют алгоритм «подъема» и запись этого алгоритма на языке С - текст функции Max_Heap_Insert: 0 1 3 7 2 2 14 4 8 8 4 0 16 9 1 15 10 5 7 9 1 10 6 3 3 7 2 2 15 4 8 8 4 16 9 1 14 10 5 9 10 6 3 7 void Max_Heap_Insert(Heap *hp, double x){ hp->v. elem[(hp->v. sz)++] = x; // помещаем в конец массива int i; for(i = hp->v. sz-1; i > 0; i = (i-1)/2) { // «подъем» if(hp->v. elem[(i-1)/2] > hp->v. elem[i]) return; swapv(&hp->v, i, (i-1)/2); // обмен с предком } } Лекция 28. 10. 13 г. 6

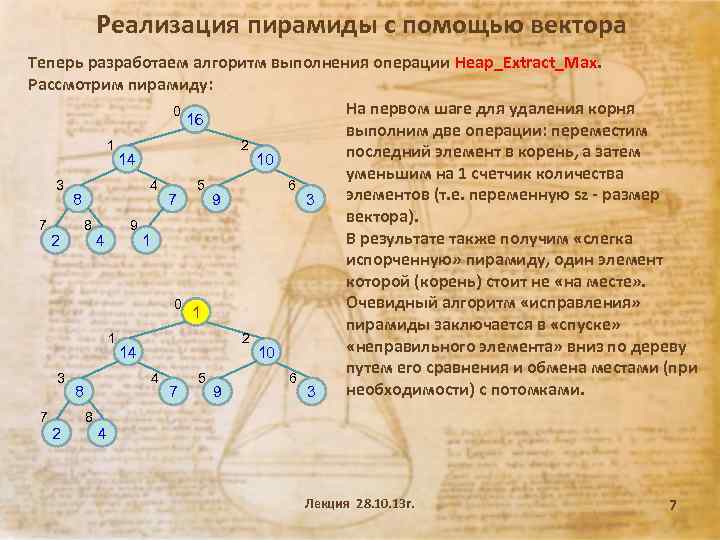Реализация пирамиды с помощью вектора Теперь разработаем алгоритм выполнения операции Heap_Extract_Max. Рассмотрим пирамиду: На первом шаге для удаления корня 0 16 выполним две операции: переместим 1 2 последний элемент в корень, а затем 14 10 уменьшим на 1 счетчик количества 3 4 5 6 элементов (т. е. переменную sz - размер 8 7 9 3 вектора). 7 8 9 В результате также получим «слегка 1 2 4 испорченную» пирамиду, один элемент которой (корень) стоит не «на месте» . Очевидный алгоритм «исправления» 0 1 пирамиды заключается в «спуске» 1 2 «неправильного элемента» вниз по дереву 14 10 путем его сравнения и обмена местами (при 3 4 5 6 необходимости) с потомками. 8 7 9 3 7 2 8 4 Лекция 28. 10. 13 г. 7

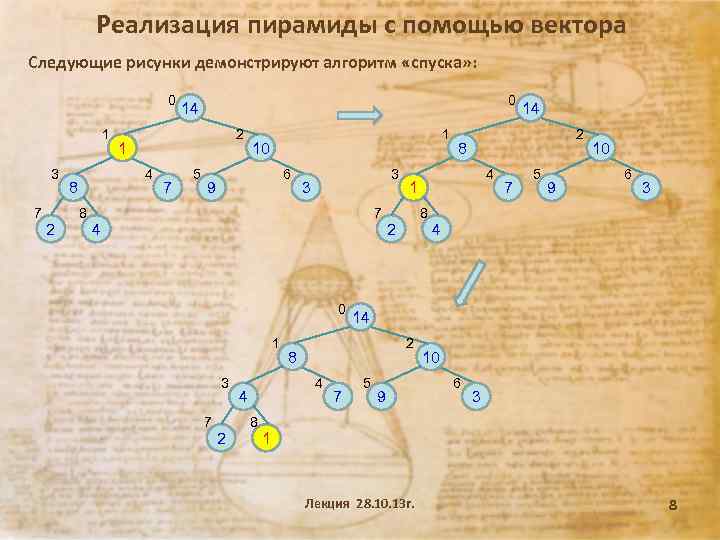Реализация пирамиды с помощью вектора Следующие рисунки демонстрируют алгоритм «спуска» : 0 1 3 7 2 2 1 4 8 8 0 14 7 5 1 10 6 9 3 3 7 4 0 1 3 7 2 4 8 1 2 2 7 8 7 5 9 10 6 3 4 14 8 4 2 4 8 14 5 9 10 6 3 1 Лекция 28. 10. 13 г. 8

Реализация пирамиды с помощью вектора Ниже приведён текст вспомогательной функции Max_Heapify, которая реализует алгоритм спуска «неправильного» элемента пирамиды с индексом i при условии, что левое и правое поддерево узла i обладают основным свойством пирамиды. void Max_Heapify(Heap *hp, int i) { int l, r, largest; l = i*2+1; r = l+1; // индексы потомков слева и справа if ((l < hp->v. sz) && (hp->v. elem[l] > hp->v. elem[i])) largest = l; else largest = i; if ((r < hp->v. sz) && (hp->v. elem[r] > hp->v. elem[largest])) largest = r; if (largest != i) { // если один из потомков больше узла i swapv(&hp->v, i, largest); // меняем местами Max_Heapify(hp, largest); // рекурсивный вызов } } Лекция 28. 10. 13 г. 9

Реализация пирамиды с помощью вектора С использованием функции Max_Heapify текст функции удаления вершины пирамиды Heap_Extract_Max будет выглядеть так: int Heap_Extract_Max(Heap *hp, double *z) { if(hp->v. sz == 0) return 0; // если пирамида пуста - выход *z = hp->v. elem[0]; hp->v. elem[0] = hp->v. elem[--(hp->v. sz)]; Max_Heapify(hp, 0); // спуск элемента, находящегося в корне return 1; } Лекция 28. 10. 13 г. 10

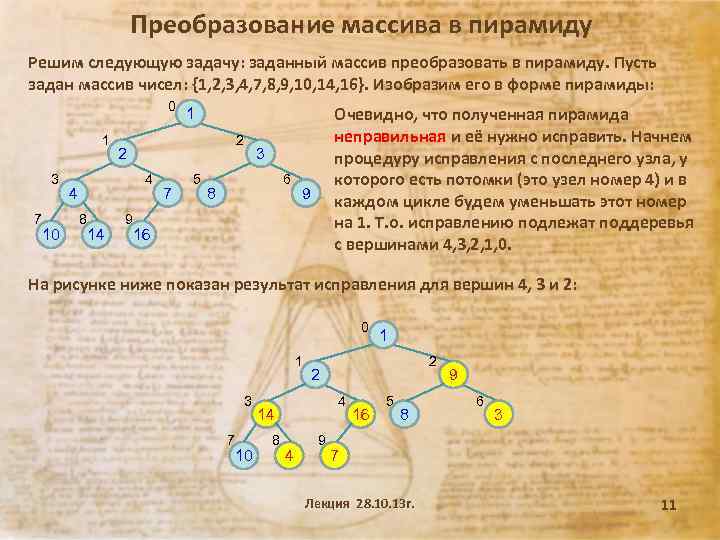Преобразование массива в пирамиду Решим следующую задачу: заданный массив преобразовать в пирамиду. Пусть задан массив чисел: {1, 2, 3, 4, 7, 8, 9, 10, 14, 16}. Изобразим его в форме пирамиды: 0 1 3 7 10 2 2 4 4 8 14 7 Очевидно, что полученная пирамида неправильная и её нужно исправить. Начнем процедуру исправления с последнего узла, у которого есть потомки (это узел номер 4) и в каждом цикле будем уменьшать этот номер на 1. Т. о. исправлению подлежат поддеревья с вершинами 4, 3, 2, 1, 0. 1 5 3 6 8 9 9 16 На рисунке ниже показан результат исправления для вершин 4, 3 и 2: 0 1 3 7 10 2 2 4 14 8 4 1 9 16 5 8 9 6 3 7 Лекция 28. 10. 13 г. 11

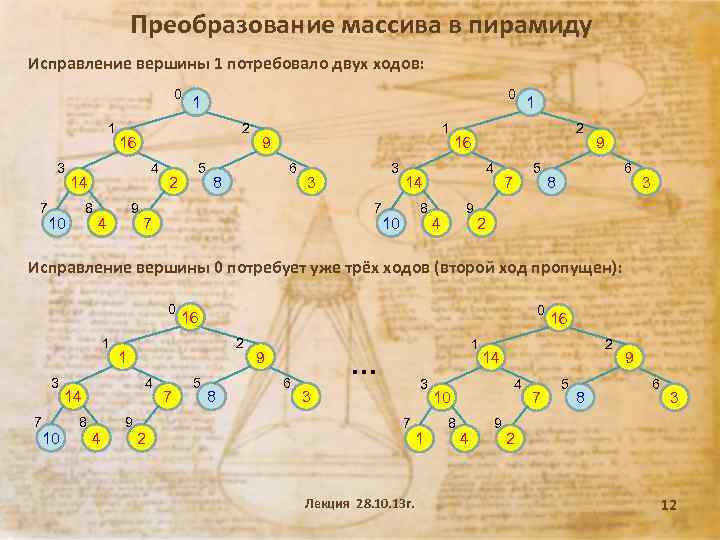Преобразование массива в пирамиду Исправление вершины 1 потребовало двух ходов: 0 1 3 7 2 16 4 14 8 10 0 1 9 4 2 5 1 9 6 8 3 3 7 7 2 16 4 14 8 10 1 9 4 5 7 9 6 8 3 2 Исправление вершины 0 потребует уже трёх ходов (второй ход пропущен): 0 1 3 7 10 2 1 4 14 8 4 0 16 9 2 7 5 8 9 6 1 … 3 3 7 1 Лекция 28. 10. 13 г. 2 14 4 10 8 4 16 9 7 5 8 9 6 3 2 12

Преобразование массива в пирамиду Описанный выше алгоритм представлен ниже в виде функции Build_Max_Heap: void Build_Max_Heap(Heap *hp) { int i; for(i=(hp->v. sz-1)/2; i >= 0; i--) Max_Heapify(hp, i); } Лекция 28. 10. 13 г. 13

Структура данных «пирамида» Теперь можно приступить к конструированию модульной структуры приложения, использующего абстракцию «пирамида» . Прежде всего, сформируем интерфейс, в который поместим описание структуры Heap, а также описания клиентских функций для работы с пирамидами: init_h, Heap_Maximum, Max_Heap_Insert, Max_Heapify, Heap_Extract_Max и Build_Max_Heap. Как отмечалось ранее, интерфейс помещается в заголовочный файл, который назовем Heap. h : // Heap. h typedef struct Heap {Vector v; } Heap; void init_h(Heap*); int Heap_Maximum(Heap*, double*); void Max_Heap_Insert(Heap*, double); void Max_Heapify(Heap*, int); int Heap_Extract_Max(Heap*, double*); void Build_Max_Heap(Heap*); Реализация всех функций, как интерфейсных, так и вспомогательных, размещается в одном файле Heap. c (не приводится). Лекция 28. 10. 13 г. 14

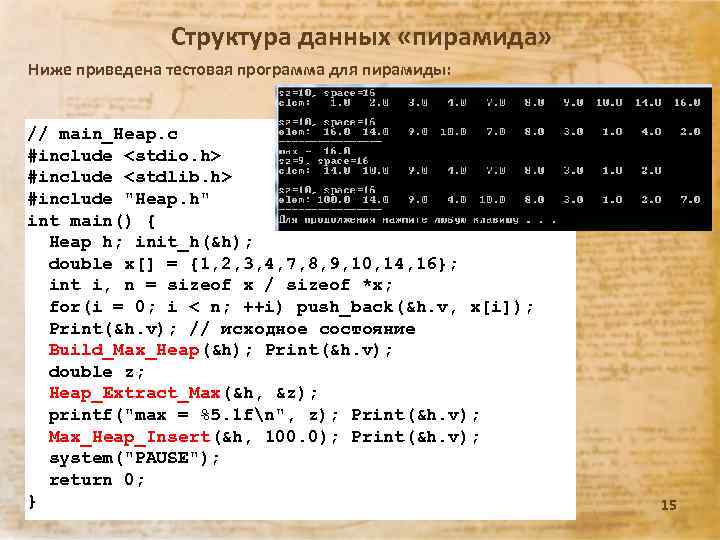Структура данных «пирамида» Ниже приведена тестовая программа для пирамиды: // main_Heap. c #include #include #include "Heap. h" int main() { Heap h; init_h(&h); double x[] = {1, 2, 3, 4, 7, 8, 9, 10, 14, 16}; int i, n = sizeof x / sizeof *x; for(i = 0; i < n; ++i) push_back(&h. v, x[i]); Print(&h. v); // исходное состояние Build_Max_Heap(&h); Print(&h. v); double z; Heap_Extract_Max(&h, &z); printf("max = %5. 1 fn", z); Print(&h. v); Max_Heap_Insert(&h, 100. 0); Print(&h. v); system("PAUSE"); return 0; } Лекция 28. 10. 13 г. 15

Структура данных «очередь с приоритетом» (priority queue) Пирамида является очень эффективным средством для реализации очереди с приоритетом – особого вида очереди, в которой в «голове очереди» всегда расположен элемент с максимальным значением ключа (т. е. имеющий максимальный приоритет). Именно этот элемент и будет первым извлекаться из очереди и направляться на обслуживание. Одна из областей применения очередей с приоритетом— планирование заданий на компьютере, который совместно используется несколькими пользователями. Очередь позволяет следить за заданиями, которые подлежат выполнению, и за их приоритетами. Если задание прервано или завершило свою работу, из очереди с помощью операции Heap_Extract_Max выбирается следующее задание с наибольшим приоритетом. В очередь в любое время можно добавить новое задание, воспользовавшись операцией Max_Heap_Insert. Лекция 28. 10. 13 г. 16