Тема 9 Динамические структуры данных Часть 2

Тема 9. Динамические структуры данных Часть 2 © С. В. Кухта, 2010

2 7. Списки © С. В. Кухта, 2010

3 Динамические структуры данных могут быть организованы Ø линейно, Ø в виде дерева Ø и в виде сети (графа). © С. В. Кухта, 2010

4 Динамические структуры данных Линейная динамическая структура представляет собой изменяемую последовательность элементов. Частными случаями таких структур являются: Ø стеки, в которых разрешено добавлять элементы только в конец и удалять только последние элементы; Ø очереди, в которых добавление элементов осуществляется в конец, а удаление – из начала; Ø деки, которые допускают добавление и удаление элементов и с начала, и с конца. © С. В. Кухта, 2010

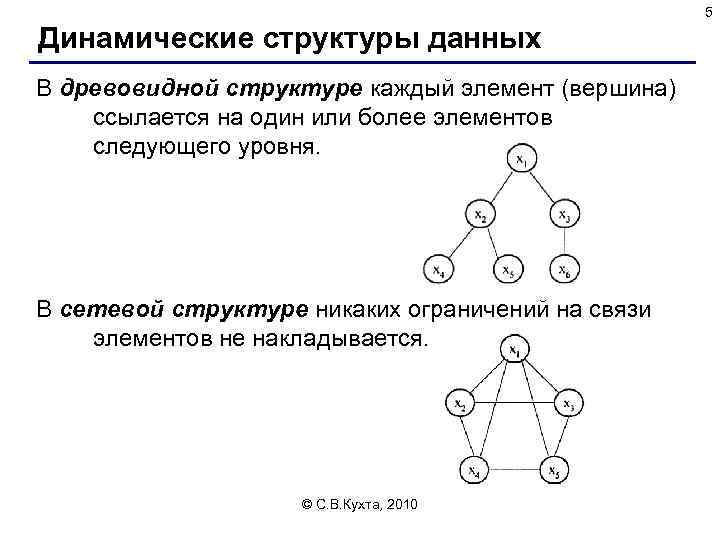5 Динамические структуры данных В древовидной структуре каждый элемент (вершина) ссылается на один или более элементов следующего уровня. В сетевой структуре никаких ограничений на связи элементов не накладывается. © С. В. Кухта, 2010

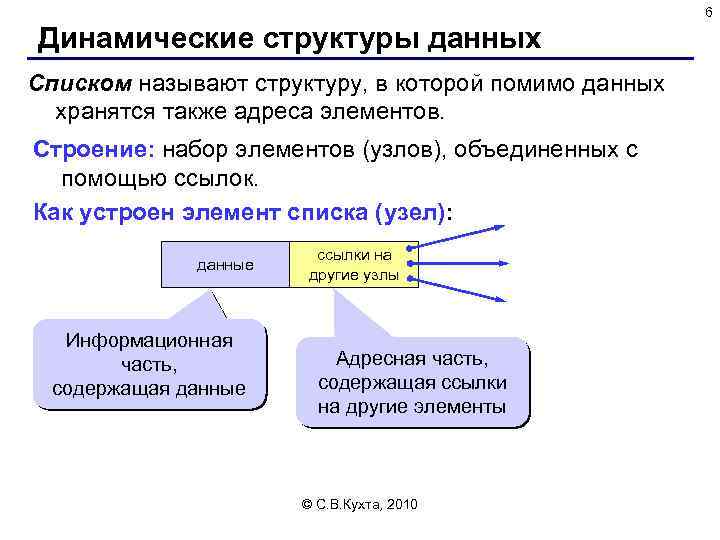6 Динамические структуры данных Списком называют структуру, в которой помимо данных хранятся также адреса элементов. Строение: набор элементов (узлов), объединенных с помощью ссылок. Как устроен элемент списка (узел): данные Информационная часть, содержащая данные ссылки на другие узлы Адресная часть, содержащая ссылки на другие элементы © С. В. Кухта, 2010

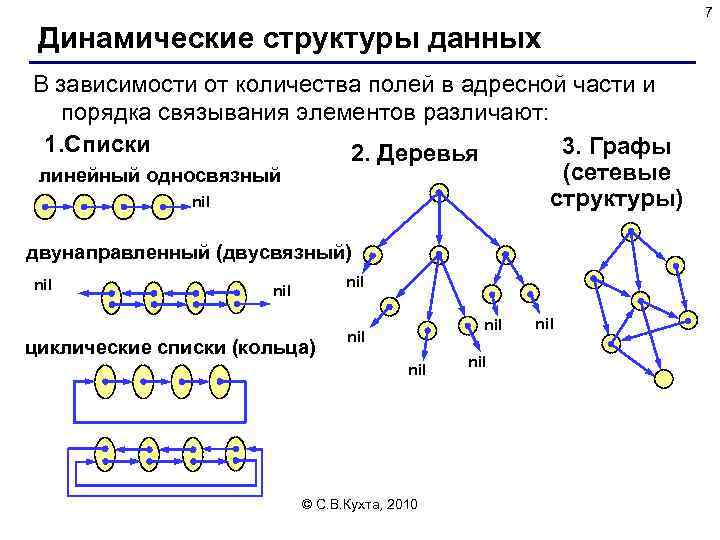7 Динамические структуры данных В зависимости от количества полей в адресной части и порядка связывания элементов различают: 1. Списки 3. Графы 2. Деревья (сетевые линейный односвязный структуры) nil двунаправленный (двусвязный) nil nil циклические списки (кольца) nil nil © С. В. Кухта, 2010 nil

8 Когда нужны списки? Задача (алфавитно-частотный словарь). В файле записан текст. Нужно записать в другой файл в столбик все слова, встречающиеся в тексте, в алфавитном порядке, и количество повторений для каждого слова. Проблемы: 1) количество слов заранее неизвестно (статический массив); 2) количество слов определяется только в конце работы (динамический массив). Решение – список. Алгоритм: 1) создать список; 2) если слова в файле закончились, то стоп. 3) прочитать слово и искать его в списке; 4) если слово найдено – увеличить счетчик повторений, иначе добавить слово в список; 5) перейти к шагу 2. © С. В. Кухта, 2010

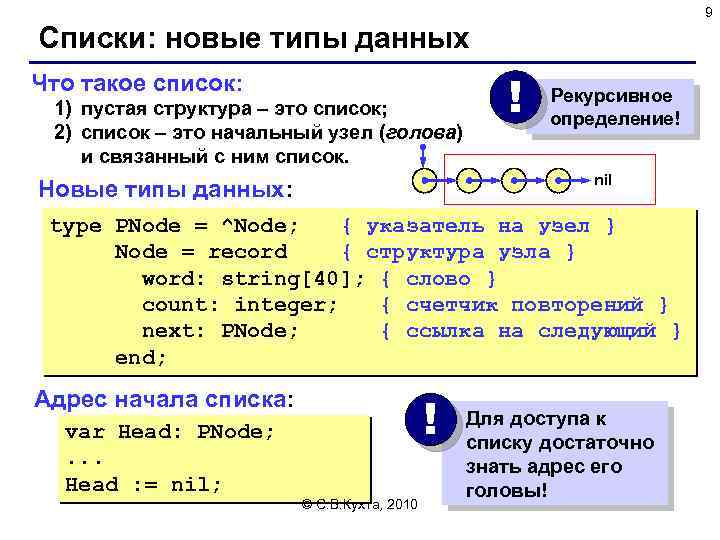9 Списки: новые типы данных Что такое список: 1) пустая структура – это список; 2) список – это начальный узел (голова) и связанный с ним список. ! Рекурсивное определение! nil Новые типы данных: type PNode = ^Node; { указатель на узел } Node = record { структура узла } word: string[40]; { слово } count: integer; { счетчик повторений } next: PNode; { ссылка на следующий } end; Адрес начала списка: var Head: PNode; . . . Head : = nil; ! © С. В. Кухта, 2010 Для доступа к списку достаточно знать адрес его головы!

10 Что нужно уметь делать со списком? 1. Создать новый узел. 2. Добавить узел: а) в начало списка; б) в конец списка; в) после заданного узла; г) до заданного узла. 3. Искать нужный узел в списке. 4. Удалить узел. © С. В. Кухта, 2010

11 Создание узла Функция Create. Node (создать узел): вход: новое слово, прочитанное из файла; выход: адрес нового узла, созданного в памяти. новое слово возвращает адрес созданного узла function Create. Node(New. Word: string): PNode; var New. Node: PNode; begin New(New. Node); New. Node^. word : = New. Word; New. Node^. count : = 1; Если память New. Node^. next : = nil; выделить не Create. Node : = New. Node; удалось? end; © С. В. Кухта, 2010 ?

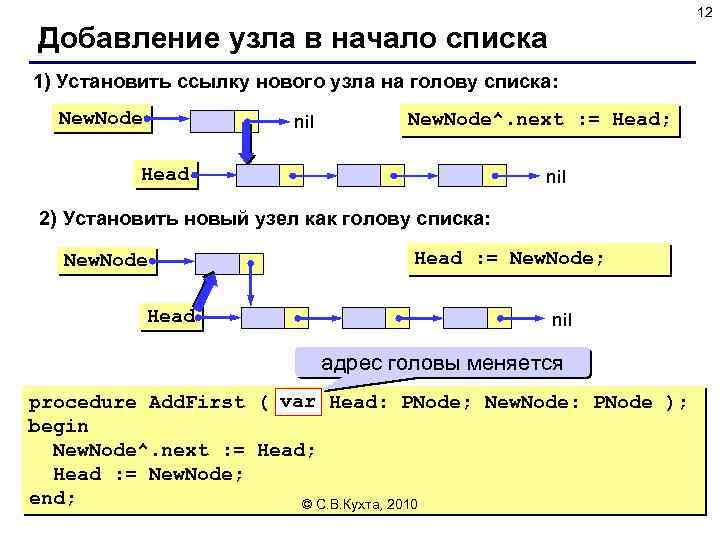12 Добавление узла в начало списка 1) Установить ссылку нового узла на голову списка: New. Node nil New. Node^. next : = Head; Head nil 2) Установить новый узел как голову списка: New. Node Head : = New. Node; nil адрес головы меняется procedure Add. First ( var Head: PNode; New. Node: PNode ); begin New. Node^. next : = Head; Head : = New. Node; end; © С. В. Кухта, 2010

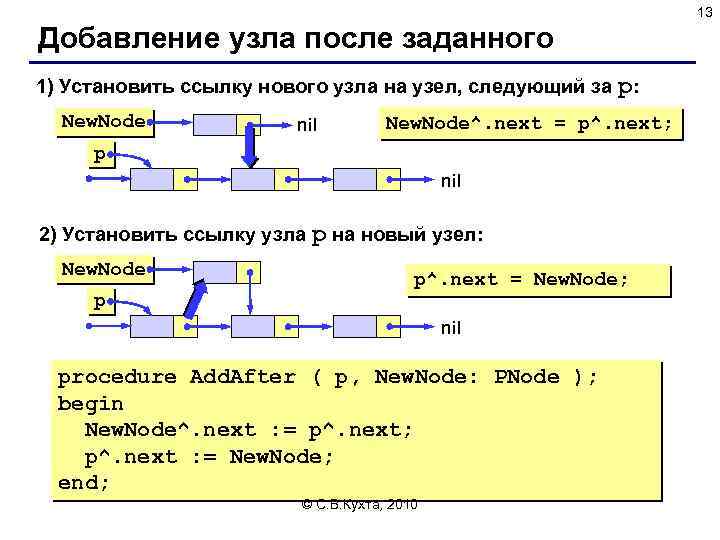13 Добавление узла после заданного 1) Установить ссылку нового узла на узел, следующий за p: New. Node nil New. Node^. next = p^. next; p nil 2) Установить ссылку узла p на новый узел: New. Node p p^. next = New. Node; nil procedure Add. After ( p, New. Node: PNode ); begin New. Node^. next : = p^. next; p^. next : = New. Node; end; © С. В. Кухта, 2010

14 Проход по списку Задача: сделать что-нибудь хорошее с каждым элементом списка. q Head nil Алгоритм: 1) установить вспомогательный указатель q на голову списка; 2) если указатель q равен nil (дошли до конца списка), то стоп; 3) выполнить действие над узлом с адресом q ; 4) перейти к следующему узлу, q^. next. var q: PNode; . . . q : = Head; // начали с головы while q <> nil do begin // пока не дошли до конца. . . // делаем что-то хорошее с q q : = q^. next; // переходим к следующему © С. В. Кухта, 2010 end;

15 Добавление узла в конец списка Задача: добавить новый узел в конец списка. Алгоритм: 1) найти последний узел q, такой что q^. next равен nil; 2) добавить узел после узла с адресом q (процедура Add. After). Особый случай: добавление в пустой список. procedure Add. Last ( var Head: PNode; New. Node: PNode ); var q: PNode; особый случай – добавление в begin пустой список if Head = nil then Add. First ( Head, New. Node ) else begin ищем последний узел q : = Head; while q^. next <> nil do q : = q^. next; добавить узел Add. After ( q, New. Node ); после узла q end; © С. В. Кухта, 2010 end;

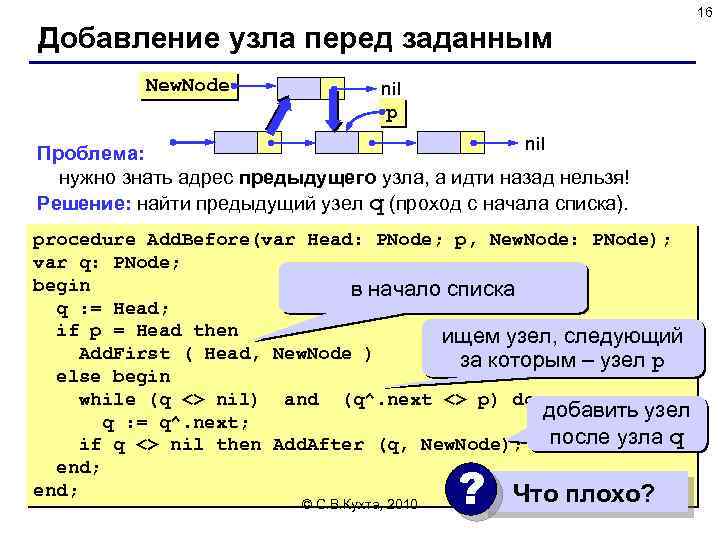16 Добавление узла перед заданным New. Node nil p nil Проблема: нужно знать адрес предыдущего узла, а идти назад нельзя! Решение: найти предыдущий узел q (проход с начала списка). procedure Add. Before(var Head: PNode; p, New. Node: PNode); var q: PNode; begin в начало списка q : = Head; if p = Head then ищем узел, следующий Add. First ( Head, New. Node ) за которым – узел p else begin while (q <> nil) and (q^. next <> p) do добавить узел q : = q^. next; if q <> nil then Add. After (q, New. Node); после узла q end; Что плохо? © С. В. Кухта, 2010 ?

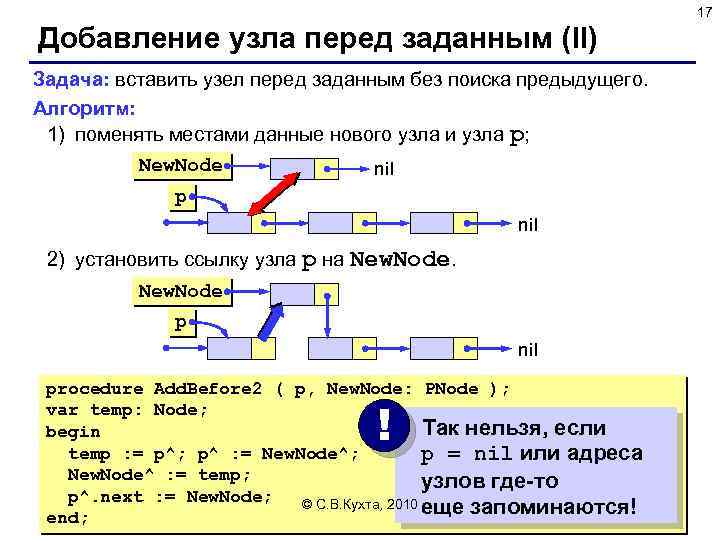17 Добавление узла перед заданным (II) Задача: вставить узел перед заданным без поиска предыдущего. Алгоритм: 1) поменять местами данные нового узла и узла p; New. Node nil p nil 2) установить ссылку узла p на New. Node p nil procedure Add. Before 2 ( p, New. Node: PNode ); var temp: Node; Так нельзя, если begin temp : = p^; p^ : = New. Node^; p = nil или адреса New. Node^ : = temp; узлов где-то p^. next : = New. Node; © С. В. Кухта, 2010 еще запоминаются! end; !

18 Поиск слова в списке Задача: найти в списке заданное слово или определить, что его нет. Функция Find: вход: слово (символьная строка); выход: адрес узла, содержащего это слово или nil. Алгоритм: проход по списку. ищем это слово результат – адрес узла или nil (нет такого) function Find(Head: PNode; New. Word: string): PNode; var q: PNode; begin q : = Head; while (q <> nil) and (New. Word <> q^. word) do q : = q^. next; Find : = q; пока не дошли до конца списка end; © С. В. Кухта, 2010 и слово не равно заданному

19 Куда вставить новое слово? Задача: найти узел, перед которым нужно вставить, заданное слово, так чтобы в списке сохранился алфавитный порядок слов. Функция Find. Place: вход: слово (символьная строка); выход: адрес узла, перед которым нужно вставить это слово или nil, если слово нужно вставить в конец списка. function Find. Place(Head: PNode; New. Word: string): PNode; var q: PNode; begin q : = Head; while (q <> nil) and (New. Word > q^. word) do q : = q^. next; Find. Place : = q; end; слово New. Word стоит по алфавиту перед q^. word © С. В. Кухта, 2010

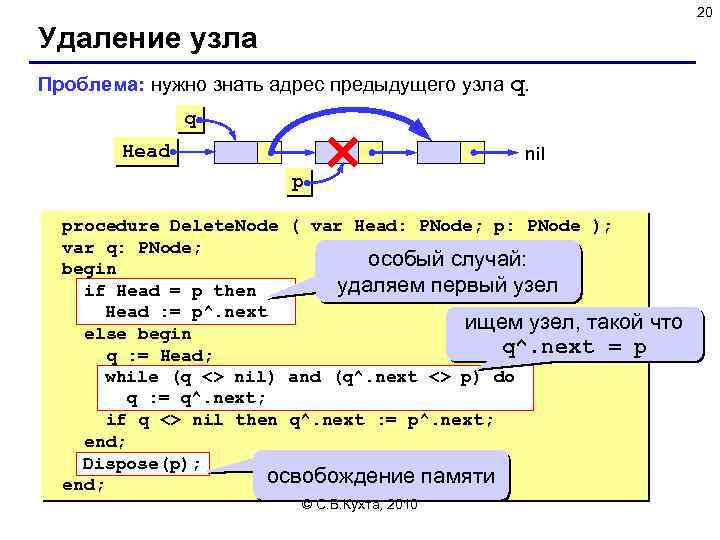20 Удаление узла Проблема: нужно знать адрес предыдущего узла q. q Head nil p procedure Delete. Node ( var Head: PNode; p: PNode ); var q: PNode; особый случай: begin удаляем первый узел if Head = p then Head : = p^. next ищем узел, такой что else begin q^. next = p q : = Head; while (q <> nil) and (q^. next <> p) do q : = q^. next; if q <> nil then q^. next : = p^. next; end; Dispose(p); освобождение памяти end; © С. В. Кухта, 2010

21 Алфавитно-частотный словарь Алгоритм: 1) открыть файл на чтение; var F: Text; . . . Assign(F, 'input. dat'); Reset ( F ); 2) 3) 4) 5) прочитать очередное слово (как? ) если файл закончился, то перейти к шагу 7; если слово найдено, увеличить счетчик (поле count); если слова нет в списке, то • создать новый узел, заполнить поля (Create. Node); • найти узел, перед которым нужно вставить слово (Find. Place); • добавить узел (Add. Before); 6) перейти к шагу 2; 7) закрыть файл Close ( F ); © С. В. Кухта, 2010 8) вывести список слов, используя проход по списку.

22 Как прочитать одно слово из файла? Алгоритм: 1) пропускаем все спецсимволы и пробелы (с кодами <= 32) 2) читаем все символы до первого пробела или спецсимвола function Get. Word ( F: Text ) : string; var c: char; begin Result : = ''; { пустая строка } c : = ' '; { пробел – чтобы войти в цикл } { пропускаем спецсимволы и пробелы } while not eof(f) and (c <= ' ') do read(F, c); { читаем слово } while not eof(f) and (c > ' ') do begin Result : = Result + c; read(F, c); end; Можно поменять местами Get. Word: = Result; © строчки в цикле? С. В. Кухта, 2010 end; ?

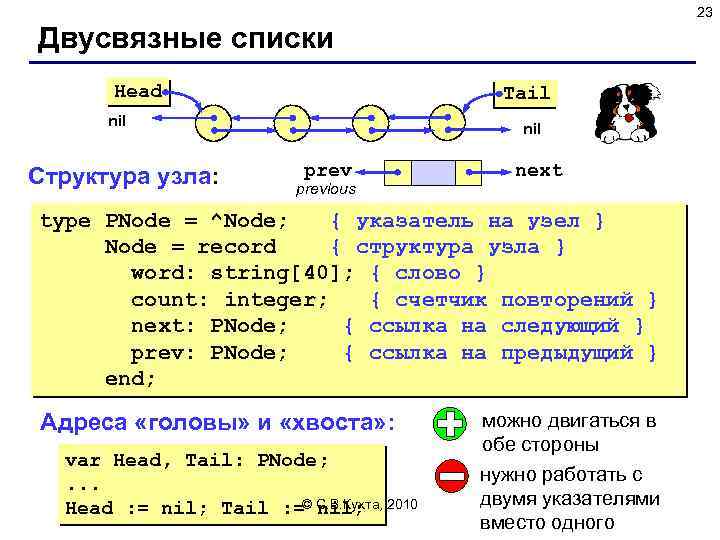23 Двусвязные списки Head Tail nil Структура узла: nil previous next type PNode = ^Node; { указатель на узел } Node = record { структура узла } word: string[40]; { слово } count: integer; { счетчик повторений } next: PNode; { ссылка на следующий } prev: PNode; { ссылка на предыдущий } end; Адреса «головы» и «хвоста» : var Head, Tail: PNode; . . . Head : = nil; Tail : =© С. В. Кухта, 2010 nil; можно двигаться в обе стороны нужно работать с двумя указателями вместо одного

24 Задания « 4» : «Собрать» из этих функций программу для построения алфавитно-частотного словаря. В конце файла вывести общее количество разных слов (количество элементов списка). « 6» : То же самое, но использовать двусвязные списки. « 8» : То же самое, что и на « 6» , но вывести список слов в порядке убывания частоты, то есть, сначала те слова, которые встречаются чаще всего. © С. В. Кухта, 2010

25 Характеристика списков Доступ Добраться к произвольному элементу можно лишь за O(n) операций. Быстрый доступ возможен лишь к 1 -му и последнему элементу списка. Удаление и вставка элементов Удаление элемента из середины списка требует O(n) операций. Но удалять элементы из начала (и конца для двунаправленных списков) списка можно за с операций (с – не зависит от длины списка). Аналогичные свойства выполняются и для вставки элемента. © С. В. Кухта, 2010

26 Характеристика списков Поиск Найти элемент можно лишь за O(n) операций независимо от того, является ли список отсортированным или нет. При этом для всех операций списки не требуют наличия непрерывного сегмента памяти, и операции, которые требуют просмотра всего списка, например, слияние двух списков, выполняются с той же скоростью, что и аналогичные операции над массивами. Несмотря на то, что скорость вставки элементов в список линейна относительно длины списка, но величина константы значительно ниже чем при вставке элемента в массив. © С. В. Кухта, 2010

27 Характеристика списков Фактически, преимущества массивов перед списками – скорость доступа к произвольному элементу и быстрый поиск в отсортированном массиве. © С. В. Кухта, 2010

28 Пример 1 Разработать программу, которая строит список, сортированный по возрастанию элементов, из целых чисел, вводимых с клавиатуры. Количество чисел не известно, но отлично от нуля. Конец ввода – по комбинации CTRL-Z (конец файла на устройстве ввода). Список сортирован, соответственно, добавляя элемент, необходимо сохранить закон сортировки: ü элемент должен вставляться перед первым элементом, который больше, чем добавляемый. В зависимости от конкретных данных он может вставляться в Ø начало, Ø середину Ø и конец списка. © С. В. Кухта, 2010

29 Пример 1 Туре tpel=^element; {тип «указатель на элемент» } element=record num: mteger; {число} p: tpel; {указатель на следующий элемент} end; Var first, {указатель списка - адрес первого элемента списка} n, f, q: tpel; {вспомогательные указатели} . . . © С. В. Кухта, 2010

30 Пример 1. . . new(first); {запрашиваем память под первый элемент} Read. Ln(first^. num); {заносим число в информ. поле} first^. p : =nil; while not EOF do begin new(q); {создаем элемент} Read. Ln(q^. num); {заносим значение} if q^. num

31 Пример 1 else begin {иначе вставляем в середину или конец} n: =first; {указатель на текущий элемент} f: =first; {указатель на предыдущий элемент} flag: =false; {"элемент не вставлен"} {цикл поиска места вставки} while (n^. p<>nil) and (not flag) do begin n: =n^. p; {переходим к следующему элементу} if q^. num

32 Пример 1 if not flag then {если элемент не вставлен, то} begin {вставляем последнего} q^. p: =nil; end; f^. p: =q; © С. В. Кухта, 2010

33 Пример 2 Разработать программу, которая удаляет из списка все элементы меньше заданного значения k. Удаляемые значения могут располагаться в списке на любом месте, следовательно, возможны четыре варианта удаления элемента, которые сводятся к двум случаям: Ø удаление единственного элемента и удаление записей из начала списка – удаление из начала списка; Ø удаление средних и последнего элементов – удаление не из начала списка. Для разделения этих двух случаев введем специальный признак «удаление из начала» , который в начале установим равным true, а затем, как только в списке будет оставлен хотя бы один элемент – изменим на © С. В. Кухта, 2010 false.

34 Пример 2 Туре tpel=^element; {тип «указатель на элемент» } element=record num: mteger; {число} p: tpel; {указатель на следующий элемент} end; Var first, {указатель списка - адрес первого элемента списка} n, f, q: tpel; {вспомогательные указатели} . . . © С. В. Кухта, 2010

35 Пример 2 n: =first; nft: =true; {признак «удаление из начала списка» } repeat if n^. num

36 Пример 2 else begin {оставляем элемент в списке} f: =n; {устанавливаем адрес предыдущего элемента} n: =n^. р; {переходим к следующему элементу} nft: =not nft { «удаление не из начала списка» } end; until n=nil; {до завершения списка}. . . © С. В. Кухта, 2010

37 Пример 3 Иногда кольцевая структура списка помогает упростить программный код. В качестве примера разберем игру в считалочку. Игра заключается в следующем: ü Несколько участников становятся в круг, затем называется целое число n. После этого каждый n-ый из участников вылетает. ü После вылета участника отсчет начинается со следующего игрока. ü Победителем считается тот, кто последний останется в списке. © С. В. Кухта, 2010

38 Пример 3 Например, если играют 7 участников (см. рисунок), n=3 и начальный элемент равен 1, то вылетать они будут в таком порядке: 3, 6, 2, 7, 5, 1. © С. В. Кухта, 2010

39 Пример 3 Type ZKnoten = ^Knoten; Knoten = record z: integer; Next: ZKnoten; end; Zykl. Liste = record Head: ZKnoten; {Head - начало} end; {Возвращает true, если пустой} function Is. Free(var L: Zykl. Liste): boolean; begin Is. Free: =L. Head=nil; end; © С. В. Кухта, 2010

40 Пример 3 {Добавляет узел, в котором будет записано число zahl} procedure Add. Knoten(var Zliste: Zykl. Liste; zahl: integer); Var zeig: ZKnoten; begin New(zeig); zeig^. z: =zahl; if Is. Free(ZListe)=true then begin zeig^. Next: =zeig; {один элемент указываtт на себя же} ZListe. Head: =zeig; exit; end; zeig^. Next: =Zliste. Head^. Next; Zliste. Head^. Next: =zeig; end; © С. В. Кухта, 2010

41 Пример 3 {Печать списка} procedure Print. List(var ZListe: Zykl. Liste); Var zeig: ZKnoten; Begin if Is. Free(ZListe)=true then exit; zeig: =ZListe. Head^. Next; repeat write (zeig^. z, ' '); zeig: =zeig^. Next; until zeig=ZListe. Head^. Next; end; © С. В. Кухта, 2010

42 Пример 3 {Освобождает память, занятую списком} procedure Tod(var ZListe: Zykl. Liste); Var zeig: ZKnoten; begin if ZListe. Head=ZListe. Head^. Next then begin {Если в списке один элемент} dispose(ZListe. Head); ZListe. Head: =nil; exit ; end; repeat {Сохраняем следующий за началом} zeig: =ZListe. Head^. Next; {Удаляем из списка} ZListe. Head^. Next: =zeig^. Next; dispose(zeig); until ZListe. Head^. Next=ZListe. Head; © С. В. Кухта, 2010 dispose(ZListe. Head); ZListe. Head: =nil;

43 Пример 3 {Считалочка, в которой выбывает каждый s-й} procedure Spiel(var LZ: Zykl. Liste; s: integer); Var zeig: ZKnoten; lauf: ZKnoten; i, q: integer; begin zeig: =LZ. Head; q: =0; writeln('!!! Считалочка !!!'); © С. В. Кухта, 2010

44 Пример 3 while zeig<>zeig^. Next do begin {Пока не остался один элемент в списке} for i: =1 to s-1 do {Пробегаем s-1 человек} zeig: =zeig^. Next; lauf: =zeig^. Next; {Запоминаем того, кто д. вылететь} {выбрасываем его из списка} zeig^. Next: =zeig^. Next; inc(q); writeln(q, '-ым выбыл ', lauf^. z); dispose(lauf); {удаляем из памяти того, кто выбыл} end; writeln('остался ', zeig^. z); {Пишем, кто же остался} LZ. Head: =zeig; {того, кто остался делаем началом} © С. В. Кухта, 2010 end;

45 Пример 3 Var ZL: Zykl. Liste; i: integer; begin writeln('Доступная память в начале работы программы ', Mem. Avail); for i: =7 downto 1 do Add. Knoten(ZL, i); Print. List(ZL); writeln('Доступная память после выделения памяти под список ', Mem. Avail); Spiel(ZL, 3); Tod(ZL); writeln('Доступная память после выхода из программы ', Mem. Avail); readln; © С. В. Кухта, 2010 end.

46 8. Стеки © С. В. Кухта, 2010

47 Стек – это линейная структура данных, в которой добавление и удаление элементов возможно только с одного конца (вершины стека). Stack (Stapel) = кипа, куча, стопка (англ. ) LIFO = Last In – First Out «Кто последним вошел, тот первым вышел» . Операции со стеком: 1) добавить элемент на вершину (Push = втолкнуть); 2) снять элемент с вершины (Pop = вылететь со звуком). © С. В. Кухта, 2010

48 Стек используется в тех случаях, когда вам надо хранить некоторое количество элементов, а доступ вам нужен лишь к тому, который вы добавили в стек последним. ü Например, если надо было проверить правильность расстановки нескольких видов скобок в строке. ü Алгоритм (без стека) может быть сведен к тому, что как только мы нашли закрывающую скобку, надо проверить, не совпадает ли она с последней свободной открывающей скобкой. © С. В. Кухта, 2010

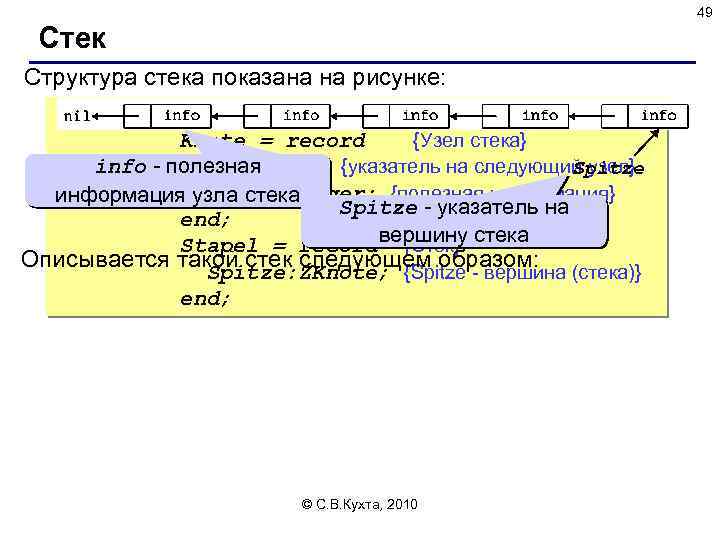49 Стек Структура стека показана на рисунке: Type ZKnote =^Knote; Knote = record {Узел стека} Next: ZKnote; {указатель на следующий узел} info - полезная Spitze infо: integer; {полезная информация} информация узла стека Spitze - указатель на end; Stapel = record вершину стека {Стек} Описывается такой стек следующем образом: (стека)} Spitze: ZKnote; {Spitze - вершина end; © С. В. Кухта, 2010

50 Пример 1 Кроме базовых операций стека – добавления элемента в стек и вытягивания элемента из него, напишем подпрограмму, которая будет печатать содержимое стека. Для того чтобы уничтожить стек из памяти, просто уничтожить его вершину недостаточно, т. к. вся остальная часть стека (кроме вершины) будет занимать место в динамической памяти, хотя получить к ней доступ в программе будет нельзя. Поэтому надо написать специальную процедуру (Tod – смерть), которая будет полностью уничтожать содержимое стека из динамической памяти (для этого надо уничтожать по очереди каждый элемент, начиная с вершины стека). © С. В. Кухта, 2010

51 Пример 1 Type ZKnote =^Knote; Knote = record {Узел стека} Next: ZKnote; {указатель на следующий узел} infо: integer; {полезная информация} end; Stapel = record {Стек} Spitze: ZKnote; {Spitze - вершина (стека)} end; {добавление элемента в стек} procedure Add(var S: Stapel; x: integer); Var z: ZKnote; begin new(z); {создаем новый узел} z^. next: =S. Spitze; {он будет находиться перед вершиной} z^. info: =х; S. Spitze: =z; © С. В. Кухта, 2010 {Делаем z вершиной стека}

52 Пример 1 {Возвращает true, если стек пуст} function Is. Free(var S: Stapel) : boolean; begin Is. Free: = S. Spitze=nil; end; {Возвращает число из вершины стека и затем уничтожает вершину} function Gib(var S: Stapel): integer; Var z: ZKnote; begin if Is. Free(S)=true then begin Gib: =-1; exit; end; {если стек пуст, возвращаем -1} z: =S. Spitze^. Next; {запоминаем следующий узел} Gib: =S. Spitze^. Info; {вытаскиваем инф-цию из вершины} © С. В. Кухта, 2010 dispose(S. Spitze); {уничтожаем вершину}

53 Пример 1 {Печать элементов стека (начиная с головы стека)} procedure Print(var S: Stapel); Var z: ZKnote; begin z: =S. Spitze; while z<>nil do begin write(z^. info, ' '); z: =z^. Next; {переходим к след. элементу стека} end; © С. В. Кухта, 2010

54 Пример 1 {Уничтожает стек} procedure Tod(var S: Stapel); Var z: ZKnote; begin while S. Spitze<>nil do begin z: =S. Spitze; S. Spitze: =S. Spitze^. Next; dispose(z); end; © С. В. Кухта, 2010

55 Пример 1 Var S: stapel; i, x: integer; Begin s. Spitze: =nil; writeln('Mem. Avail ', Mem. Avail); {Сколько памяти доступно в начале программы} for i: =l to 10 do {добавляем элемены в стек} Add(S, i); write('Наш стек: '); Print(S); writeln('Извлекаем 5 элементов из стека'); for i: =1 to 5 do write(Gib(S), ' ' ); writeln('Что осталось от стека '); Print(S); writeln; Tod(S); {уничтожаем стек из динамической памяти} © С. В. Кухта, 2010 writeln('Mem. Avail ', Mem. Avail); {Проверяем, вся

56 Пример 2 Задача: вводится символьная строка, в которой записано выражение со скобками трех типов: [], {} и (). Определить, верно ли расставлены скобки (не обращая внимания на остальные символы). Примеры: [()]{} ][ [({)]} Упрощенная задача: то же самое, но с одним видом скобок. Решение: счетчик вложенности скобок. Последовательность правильная, если в конце счетчик равен нулю и проходе не разу не становился отрицательным. ( ( ) ) ( ) 1 2 1 0 ? ( ( ) ) ) ( 1 2 1 0 -1 0 Можно ли решить исходную задачу так же, но с тремя счетчиками? © С. В. Кухта, 2010 ( ( ) ) ( 1 2 1 0 1 [ ( { ) ] } (: 0 1 0 [: 0 1 0 {: 0 1 0

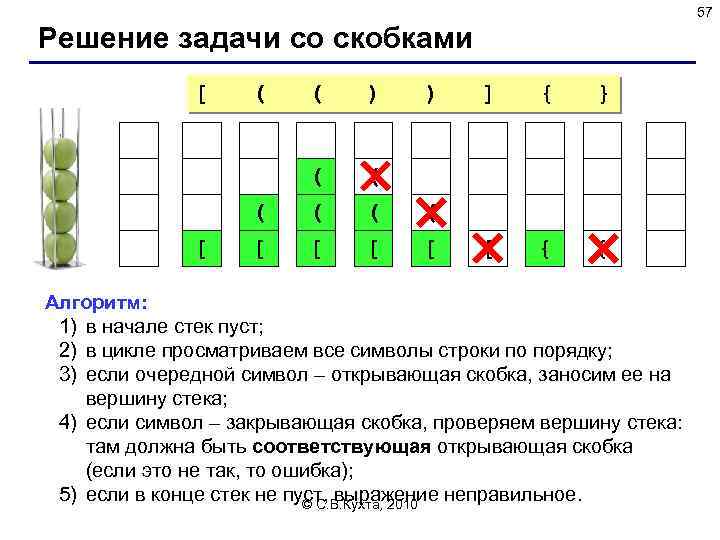57 Решение задачи со скобками [ [ ( ( [ ( ) ) ( ( [ ( [ [ ] { } [ { { Алгоритм: 1) в начале стек пуст; 2) в цикле просматриваем все символы строки по порядку; 3) если очередной символ – открывающая скобка, заносим ее на вершину стека; 4) если символ – закрывающая скобка, проверяем вершину стека: там должна быть соответствующая открывающая скобка (если это не так, то ошибка); 5) если в конце стек не пуст, выражение неправильное. © С. В. Кухта, 2010

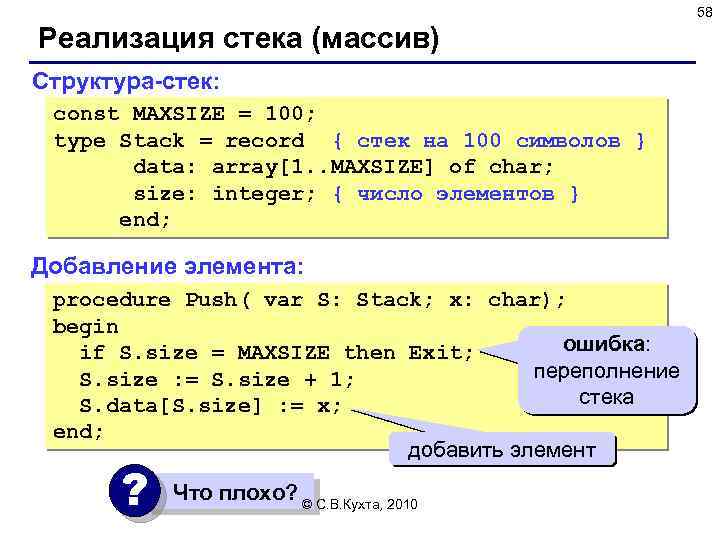58 Реализация стека (массив) Структура-стек: const MAXSIZE = 100; type Stack = record { стек на 100 символов } data: array[1. . MAXSIZE] of char; size: integer; { число элементов } end; Добавление элемента: procedure Push( var S: Stack; x: char); begin ошибка: if S. size = MAXSIZE then Exit; переполнение S. size : = S. size + 1; стека S. data[S. size] : = x; end; добавить элемент ? Что плохо? © С. В. Кухта, 2010

59 Реализация стека (массив) Снятие элемента с вершины: function Pop ( var S: Stack ): char; begin if S. size = 0 then begin ошибка: Pop : = char(255); стек пуст Exit; end; Pop : = S. data[S. size]; S. size : = S. size - 1; end; Пустой или нет? function is. Empty ( S: Stack ): Boolean; begin is. Empty : = (S. size = 0); end; © С. В. Кухта, 2010

60 Программа var br 1, br 2, expr: string; i, k: integer; upper: char; { то, что сняли со стека } error: Boolean; { признак ошибки } S: Stack; открывающие скобки begin br 1 : = '([{'; br 2 : = ')]}'; закрывающие скобки S. size : = 0; error : = False; writeln('Введите выражение со скобками'); readln(expr); . . . { здесь будет основной цикл обработки } if not error and is. Empty(S) then writeln('Выражение правильное. ') else writeln('Выражение неправильное. ') end. © С. В. Кухта, 2010

61 Обработка строки (основной цикл) цикл по всем символам for i: =1 to length(expr) строки expr do begin цикл по всем видам скобок for k: =1 to 3 do begin if expr[i] = br 1[k] then begin { откр. скобка } Push(S, expr[i]); { втолкнуть в стек} break; end; if expr[i] = br 2[k] then begin { закр. скобка } upper : = Pop(S); { снять символ со стека } error : = upper <> br 1[k]; ошибка: стек пуст break; или не та скобка end; if error then break; была ошибка: дальше нет © С. В. Кухта, 2010 смысла проверять end;

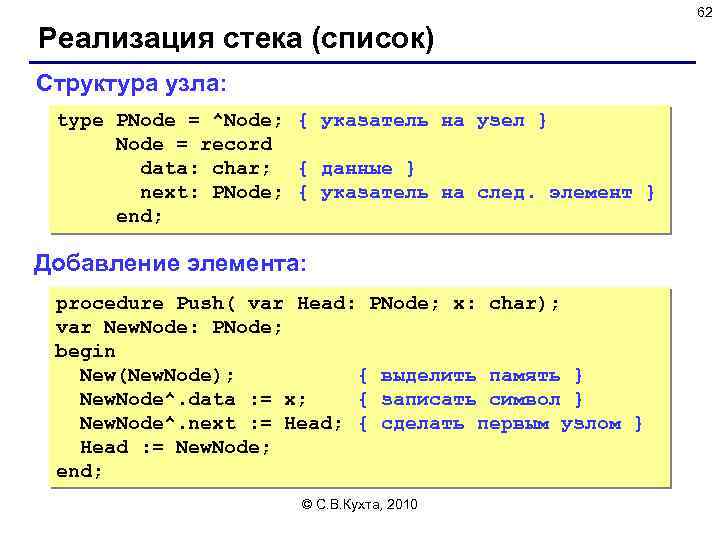62 Реализация стека (список) Структура узла: type PNode = ^Node; { указатель на узел } Node = record data: char; { данные } next: PNode; { указатель на след. элемент } end; Добавление элемента: procedure Push( var Head: PNode; x: char); var New. Node: PNode; begin New(New. Node); { выделить память } New. Node^. data : = x; { записать символ } New. Node^. next : = Head; { сделать первым узлом } Head : = New. Node; end; © С. В. Кухта, 2010

63 Реализация стека (список) Снятие элемента с вершины: function Pop ( var Head: PNode ): char; var q: PNode; begin if Head = nil then begin { стек пуст } Pop : = char(255); { неиспользуемый символ } Exit; end; Pop : = Head^. data; { взять верхний символ } { запомнить вершину } q : = Head; Head : = Head^. next; { удалить вершину из стека } { удалить из памяти } Dispose(q); end; ? Можно ли переставлять операторы? © С. В. Кухта, 2010

64 Реализация стека (список) Пустой или нет? function is. Empty ( S: Stack ): Boolean; begin is. Empty : = (S = nil); end; Изменения в основной программе: var S: Stack; . . . S. size : = 0; ! var S: PNode; S : = nil; Больше ничего не меняется! © С. В. Кухта, 2010

65 Вычисление арифметических выражений Как вычислять автоматически: (a + b) / (c + d – 1) Инфиксная запись (знак операции между операндами) необходимы скобки! Префиксная запись (знак операции до операндов) польская нотация, / + a b - c + - 1 a + c d 1 + d Jan Łukasiewicz (1920) скобки не нужны, можно однозначно вычислить! Постфиксная запись (знак операции после операндов) a b + c d + - 1 / + b c + d 1 - обратная польская нотация, © С. В. Кухта, 2010 F. L. Bauer and E. W. Dijkstra

66 Запишите в постфиксной форме (32*6 -5)*(2*3+4)/(3+7*2) (2*4+3*5)*(2*3+18/3*2)*(12 -3) (4 -2*3)*(3 -12/3/4)*(24 -3*12) © С. В. Кухта, 2010

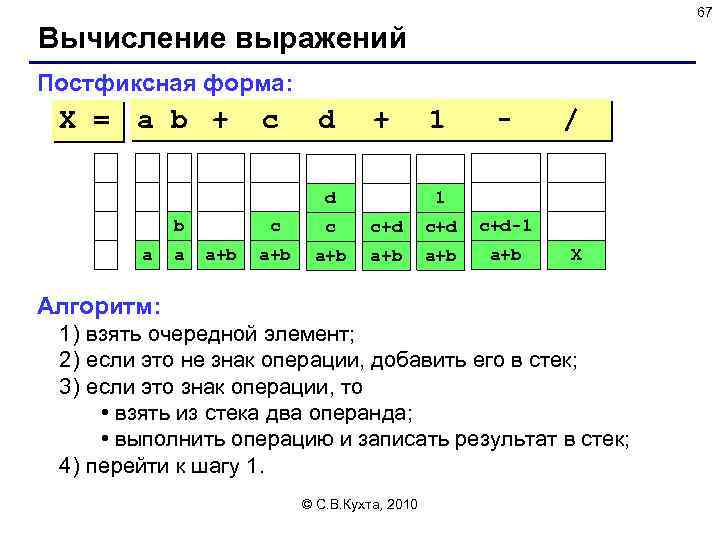67 Вычисление выражений Постфиксная форма: X = a b + c d + d b a a 1 - 1 c a+b / c c+d c+d-1 a+b a+b a+b X Алгоритм: 1) взять очередной элемент; 2) если это не знак операции, добавить его в стек; 3) если это знак операции, то • взять из стека два операнда; • выполнить операцию и записать результат в стек; 4) перейти к шагу 1. © С. В. Кухта, 2010

68 Системный стек (Windows – 1 Мб) Используется для 1) размещения локальных переменных; 2) хранения адресов возврата (по которым переходит программа после выполнения функции или процедуры); 3) передачи параметров в функции и процедуры; 4) временного хранения данных (в программах на языке Ассмеблер). Переполнение стека (stack overflow): 1) слишком много локальных переменных (выход – использовать динамические массивы); 2) очень много рекурсивных вызовов функций и процедур (выход – переделать алгоритм так, чтобы уменьшить глубину рекурсии или отказаться от нее вообще). © С. В. Кухта, 2010

69 9. Очереди © С. В. Кухта, 2010

70 Очередь 6 5 4 3 2 1 Очередь – это линейная структура данных, в которой добавление элементов возможно только с одного конца (конца очереди), а удаление элементов – только с другого конца (начала очереди). FIFO = First In – First Out «Кто первым вошел, тот первым вышел» . Операции с очередью: 1) добавить элемент в конец очереди (Push. Tail = втолкнуть в конец); 2) удалить элемент с начала очереди (Pop). © С. В. Кухта, 2010

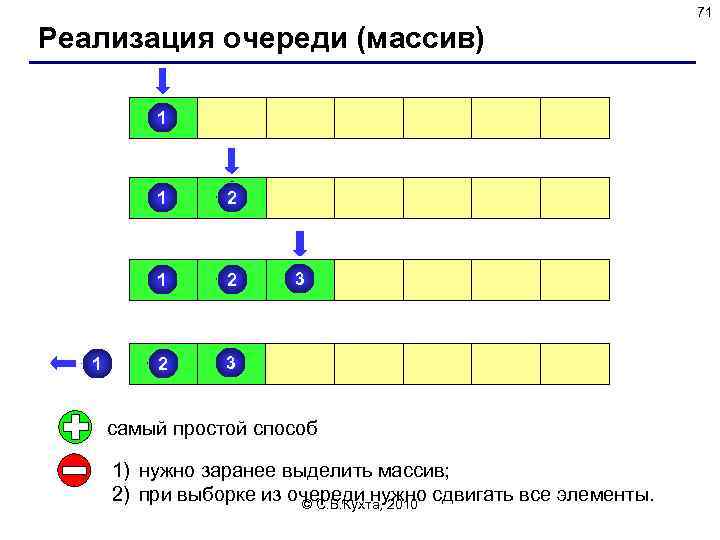71 Реализация очереди (массив) 1 1 2 2 2 3 3 самый простой способ 1) нужно заранее выделить массив; 2) при выборке из очереди нужно сдвигать все элементы. © С. В. Кухта, 2010

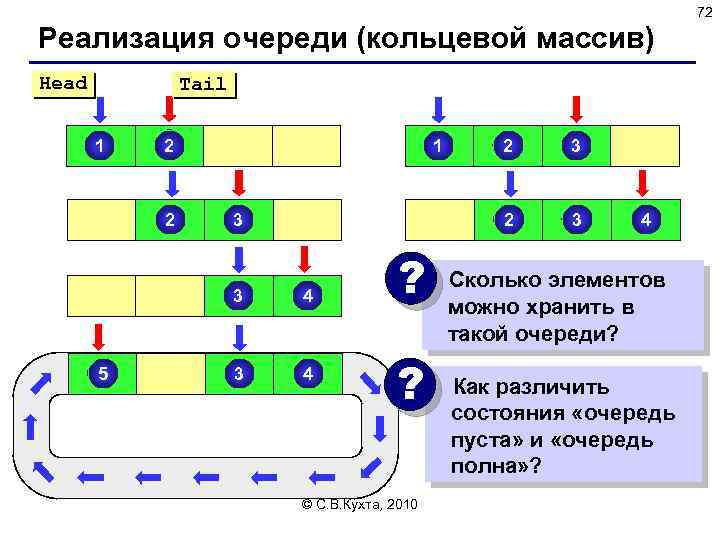72 Реализация очереди (кольцевой массив) Head Tail 1 2 2 3 3 5 4 3 4 ? ? © С. В. Кухта, 2010 2 3 2 1 3 4 Сколько элементов можно хранить в такой очереди? Как различить состояния «очередь пуста» и «очередь полна» ?

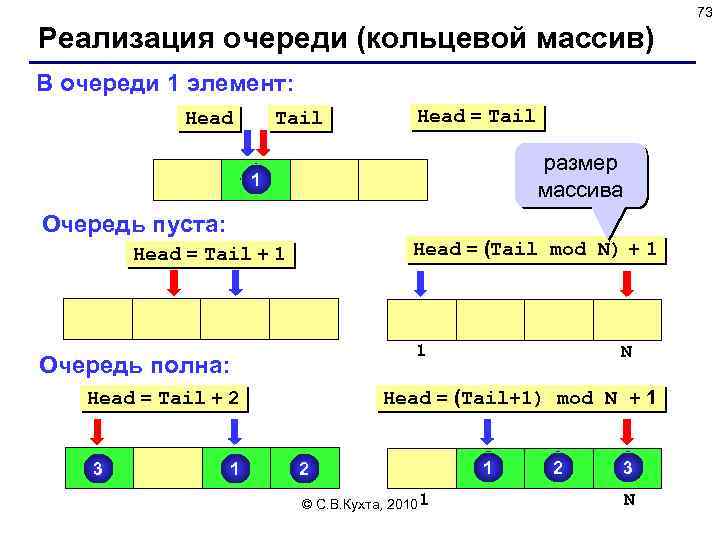73 Реализация очереди (кольцевой массив) В очереди 1 элемент: Head Tail Head = Tail размер массива 1 Очередь пуста: Head = (Tail mod N) + 1 Head = Tail + 1 1 Очередь полна: Head = (Tail+1) mod N + 1 Head = Tail + 2 3 1 N 2 © С. В. Кухта, 20101 1 2 3 N

74 Реализация очереди (кольцевой массив) Структура данных: type Queue = record data: array[1. . MAXSIZE] of integer; head, tail: integer; end; Добавление в очередь: procedure Push. Tail( var Q: Queue; x: integer); begin замкнуть в кольцо if Q. head = (Q. tail+1) mod MAXSIZE + 1 then Exit; { очередь полна, не добавить } Q. tail : = Q. tail mod MAXSIZE + 1; Q. data[Q. tail] : = x; end; © С. В. Кухта, 2010

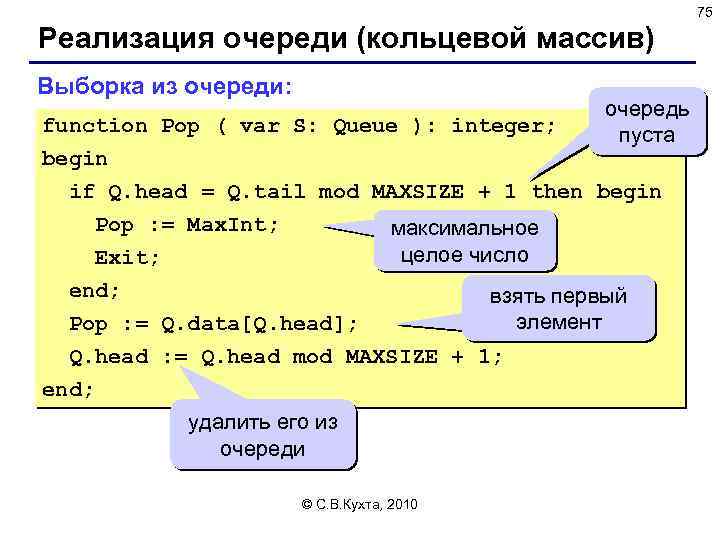75 Реализация очереди (кольцевой массив) Выборка из очереди: очередь пуста function Pop ( var S: Queue ): integer; begin if Q. head = Q. tail mod MAXSIZE + 1 then begin Pop : = Max. Int; максимальное целое число Exit; end; взять первый элемент Pop : = Q. data[Q. head]; Q. head : = Q. head mod MAXSIZE + 1; end; удалить его из очереди © С. В. Кухта, 2010

76 Реализация очереди (списки) Структура узла: type PNode = ^Node; Node = record data: integer; next: PNode; end; Тип данных «очередь» : type Queue = record head, tail: PNode; end; © С. В. Кухта, 2010

77 Реализация очереди (списки) Добавление элемента: procedure Push. Tail( var Q: Queue; x: integer ); var New. Node: PNode; создаем begin новый узел New(New. Node); если в списке уже New. Node^. data : = x; что-то было, New. Node^. next : = nil; добавляем в конец if Q. tail <> nil then Q. tail^. next : = New. Node; Q. tail : = New. Node; { новый узел – в конец} if Q. head = nil then Q. head : = Q. tail; end; если в списке © С. В. Кухта, ничего не было, … 2010

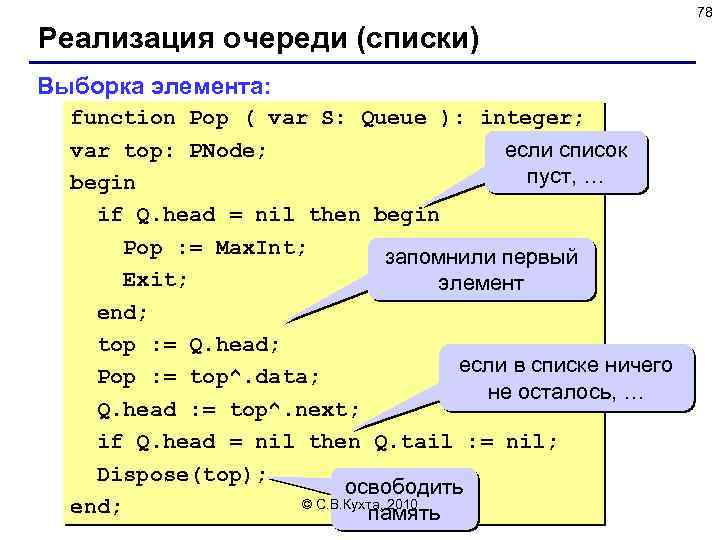78 Реализация очереди (списки) Выборка элемента: function Pop ( var S: Queue ): integer; var top: PNode; если список пуст, … begin if Q. head = nil then begin Pop : = Max. Int; запомнили первый Exit; элемент end; top : = Q. head; если в списке ничего Pop : = top^. data; не осталось, … Q. head : = top^. next; if Q. head = nil then Q. tail : = nil; Dispose(top); освободить © С. В. Кухта, 2010 end; память

79 10. Дек © С. В. Кухта, 2010

80 Дек (deque = double ended queue, очередь с двумя концами) – это линейная структура данных, в которой добавление и удаление элементов возможно с обоих концов. 6 4 2 1 3 5 Операции с деком: 1) добавление элемента в начало (Push); 2) удаление элемента с начала (Pop); 3) добавление элемента в конец (Push. Tail); 4) удаление элемента с конца (Pop. Tail). Реализация: 1) кольцевой массив; 2) двусвязный список. © С. В. Кухта, 2010

81 Задания « 4» : В файле input. dat находится список чисел (или слов). Переписать его в файл output. dat в обратном порядке. « 8» : Составить программу, которая вычисляет значение арифметического выражения, записанного в постфиксной форме, с помощью стека. Выражение правильное, допускаются только однозначные числа и знаки +, -, *, /. « 8» : То же самое, что и на « 8» , но допускаются многозначные числа. © С. В. Кухта, 2010

82 11. Деревья © С. В. Кухта, 2010

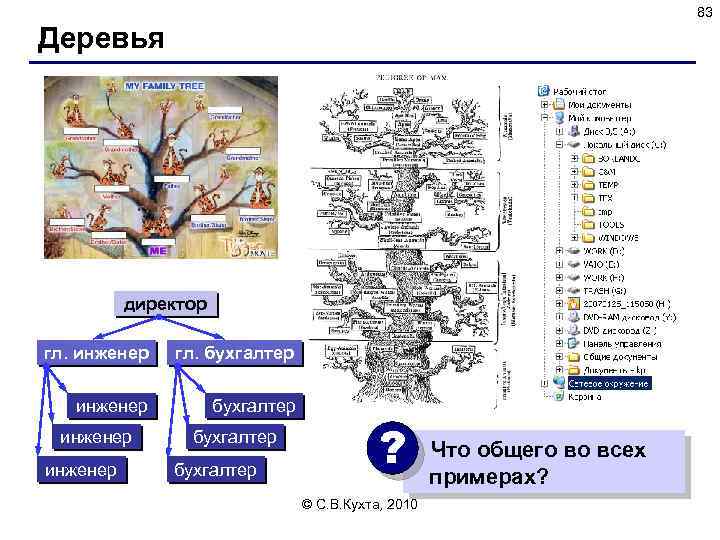83 Деревья директор гл. инженер гл. бухгалтер инженер бухгалтер ? © С. В. Кухта, 2010 Что общего во всех примерах?

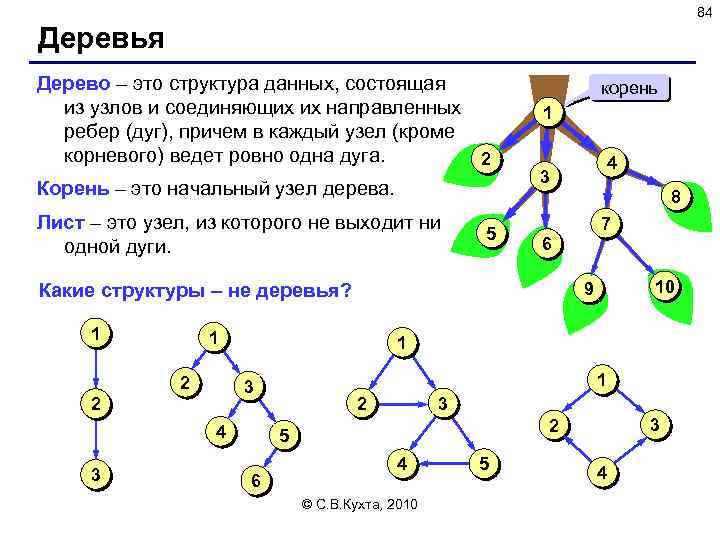84 Деревья Дерево – это структура данных, состоящая из узлов и соединяющих их направленных ребер (дуг), причем в каждый узел (кроме корневого) ведет ровно одна дуга. 2 Корень – это начальный узел дерева. Лист – это узел, из которого не выходит ни одной дуги. 5 корень 1 6 1 4 3 1 3 2 10 9 1 2 8 7 Какие структуры – не деревья? 1 4 3 2 3 6 3 2 5 4 © С. В. Кухта, 2010 5 4

85 Деревья ! С помощью деревьев изображаются отношения подчиненности (иерархия, «старший – младший» , «родитель – ребенок» ). Предок узла x – это узел, из которого существует путь по стрелкам в узел x. Потомок узла x – это узел, в который существует путь по стрелкам из узла x. Родитель узла x – это узел, из которого существует дуга непосредственно в узел x. 1 2 3 4 5 6 Сын узла x – это узел, в который существует дуга непосредственно из узла x. Брат узла x (sibling) – это узел, у которого тот же родитель, что и у узла x. Высота дерева – это наибольшее расстояние от корня до листа © С. В. Кухта, 2010 (количество дуг).

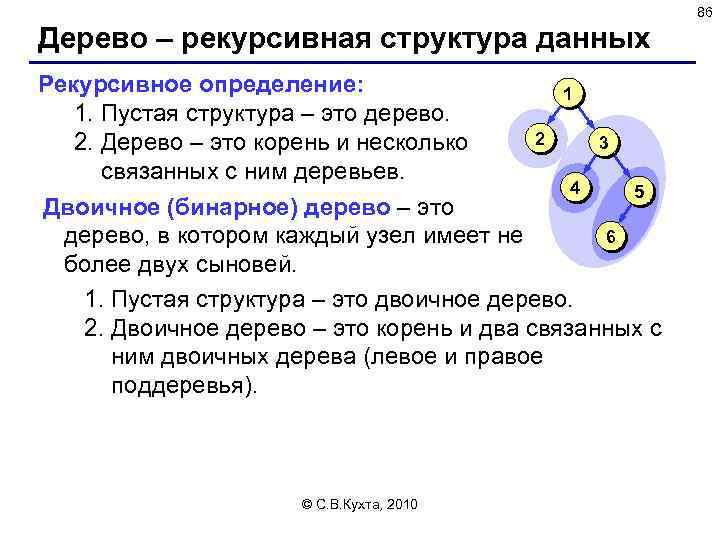86 Дерево – рекурсивная структура данных Рекурсивное определение: 1 1. Пустая структура – это дерево. 2 3 2. Дерево – это корень и несколько связанных с ним деревьев. 4 5 Двоичное (бинарное) дерево – это 6 дерево, в котором каждый узел имеет не более двух сыновей. 1. Пустая структура – это двоичное дерево. 2. Двоичное дерево – это корень и два связанных с ним двоичных дерева (левое и правое поддеревья). © С. В. Кухта, 2010

87 Двоичные деревья Применение: 1) поиск данных в специально построенных деревьях (базы данных); 2) сортировка данных; 3) вычисление арифметических выражений; 4) кодирование (метод Хаффмана). Структура узла: type PNode = ^Node; { указатель на узел } Node = record data: integer; { полезные данные } left, right: PNode; { ссылки на левого и правого сыновей } end; © С. В. Кухта, 2010

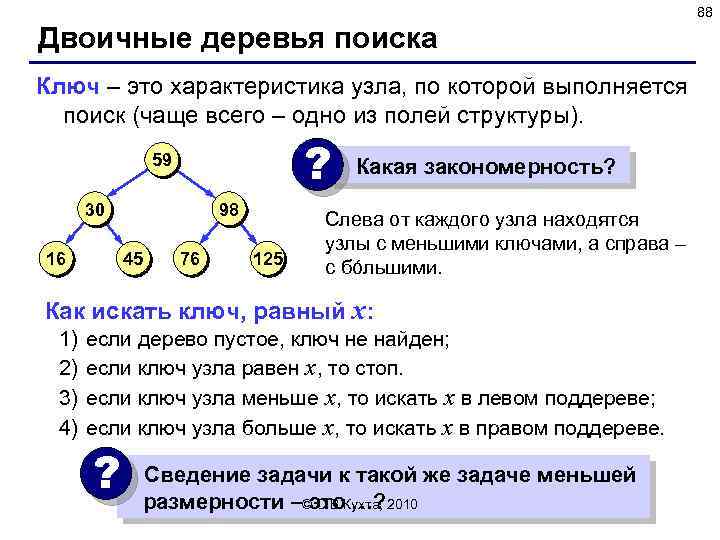88 Двоичные деревья поиска Ключ – это характеристика узла, по которой выполняется поиск (чаще всего – одно из полей структуры). ? 59 30 16 98 45 76 125 Какая закономерность? Слева от каждого узла находятся узлы с меньшими ключами, а справа – с бóльшими. Как искать ключ, равный x: 1) 2) 3) 4) если дерево пустое, ключ не найден; если ключ узла равен x, то стоп. если ключ узла меньше x, то искать x в левом поддереве; если ключ узла больше x, то искать x в правом поддереве. ? Сведение задачи к такой же задаче меньшей С. В. Кухта, размерности –©это …? 2010

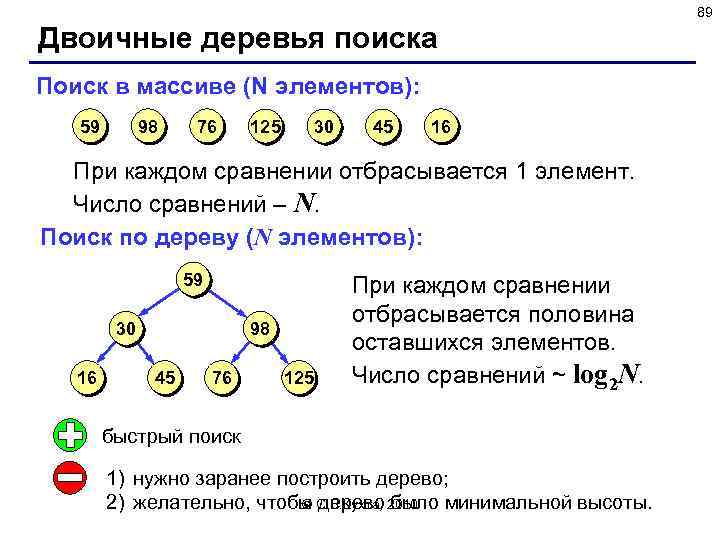89 Двоичные деревья поиска Поиск в массиве (N элементов): 59 98 76 125 30 45 16 При каждом сравнении отбрасывается 1 элемент. Число сравнений – N. Поиск по дереву (N элементов): 59 30 16 98 45 76 125 При каждом сравнении отбрасывается половина оставшихся элементов. Число сравнений ~ log 2 N. быстрый поиск 1) нужно заранее построить дерево; © дерево было 2) желательно, чтобы С. В. Кухта, 2010 минимальной высоты.

90 Реализация алгоритма поиска { Функция Search – поиск по дереву Вход: Tree - адрес корня, x - что ищем Выход: адрес узла или nil (не нашли) } function Search(Tree: PNode; x: integer): PNode; begin дерево пустое: if Tree = nil then begin ключ не нашли… Search : = nil; Exit; end; нашли, if x = Tree^. data then возвращаем Search : = Tree искать в адрес корня else левом поддереве if x < Tree^. data then Search : = Search(Tree^. left, x) else Search : = Search(Tree^. right, x); © С. В. Кухта, 2010 end; искать в правом поддереве

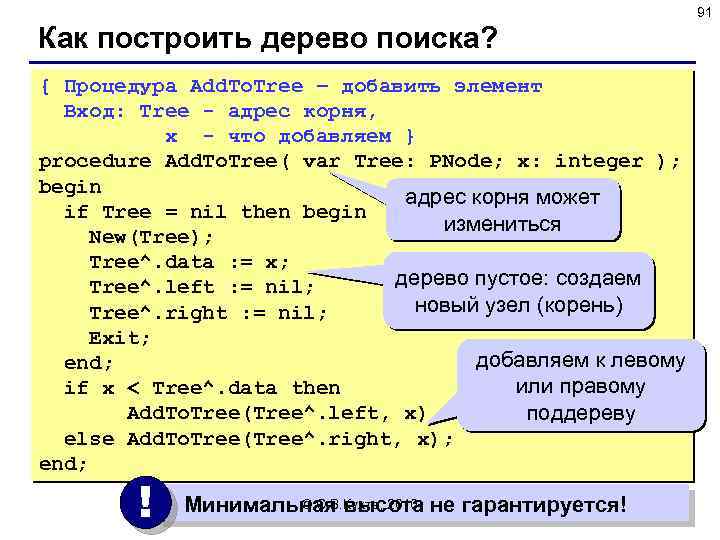91 Как построить дерево поиска? { Процедура Add. To. Tree – добавить элемент Вход: Tree - адрес корня, x - что добавляем } procedure Add. To. Tree( var Tree: PNode; x: integer ); begin адрес корня может if Tree = nil then begin измениться New(Tree); Tree^. data : = x; дерево пустое: создаем Tree^. left : = nil; новый узел (корень) Tree^. right : = nil; Exit; добавляем к левому end; или правому if x < Tree^. data then Add. To. Tree(Tree^. left, x) поддереву else Add. To. Tree(Tree^. right, x); end; ! © С. В. Кухта, 2010 Минимальная высота не гарантируется!

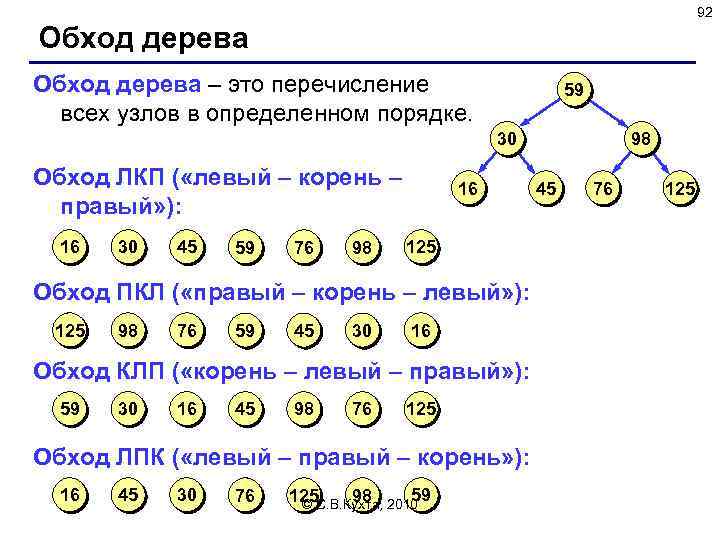92 Обход дерева – это перечисление всех узлов в определенном порядке. 59 30 Обход ЛКП ( «левый – корень – правый» ): 16 30 45 59 76 98 16 125 Обход ПКЛ ( «правый – корень – левый» ): 125 98 76 59 45 30 16 Обход КЛП ( «корень – левый – правый» ): 59 30 16 45 98 76 125 Обход ЛПК ( «левый – правый – корень» ): 16 45 30 76 59 125 С. В. Кухта, 2010 98 © 98 45 76 125

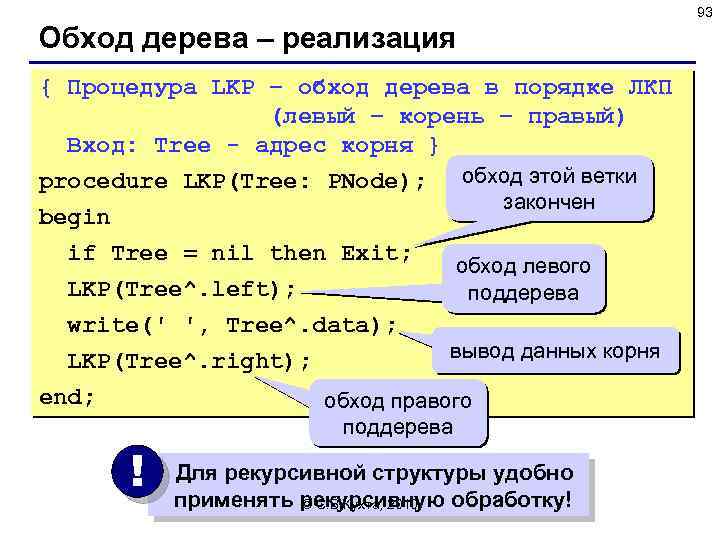93 Обход дерева – реализация { Процедура LKP – обход дерева в порядке ЛКП (левый – корень – правый) Вход: Tree - адрес корня } procedure LKP(Tree: PNode); обход этой ветки закончен begin if Tree = nil then Exit; обход левого LKP(Tree^. left); поддерева write(' ', Tree^. data); LKP(Tree^. right); end; ! вывод данных корня обход правого поддерева Для рекурсивной структуры удобно применять рекурсивную обработку! © С. В. Кухта, 2010

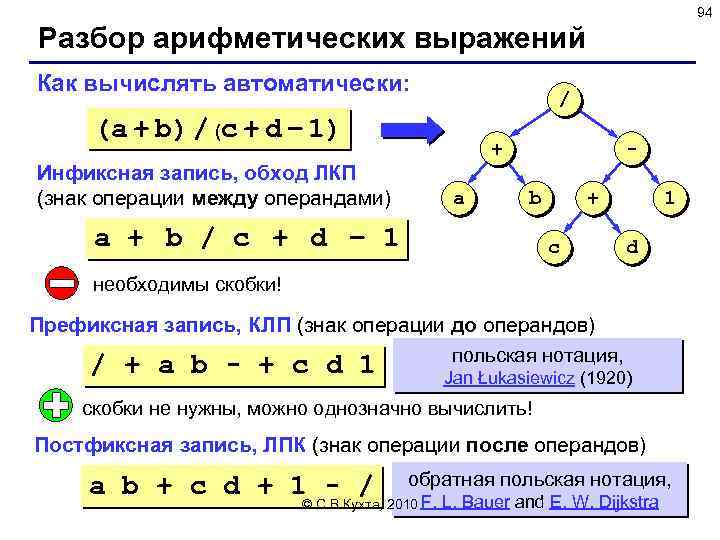94 Разбор арифметических выражений Как вычислять автоматически: / (a + b) / (c + d – 1) + Инфиксная запись, обход ЛКП (знак операции между операндами) a b a + b / c + d – 1 + c 1 d необходимы скобки! Префиксная запись, КЛП (знак операции до операндов) польская нотация, / + a b - + c d 1 Jan Łukasiewicz (1920) скобки не нужны, можно однозначно вычислить! Постфиксная запись, ЛПК (знак операции после операндов) a b + c d + 1 - / обратная польская нотация, © С. В. Кухта, 2010 F. L. Bauer and E. W. Dijkstra

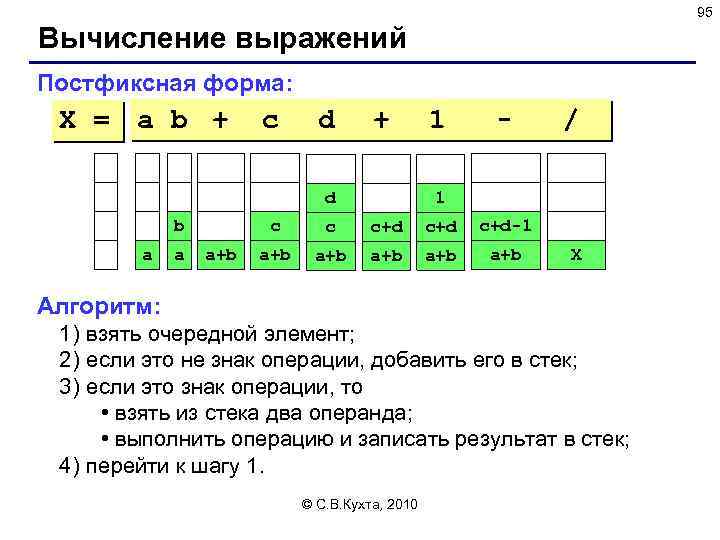95 Вычисление выражений Постфиксная форма: X = a b + c d + d b a a 1 - 1 c a+b / c c+d c+d-1 a+b a+b a+b X Алгоритм: 1) взять очередной элемент; 2) если это не знак операции, добавить его в стек; 3) если это знак операции, то • взять из стека два операнда; • выполнить операцию и записать результат в стек; 4) перейти к шагу 1. © С. В. Кухта, 2010

96 Вычисление выражений Задача: в символьной строке записано правильное арифметическое выражение, которое может содержать только однозначные числа и знаки операций +-*. Вычислить это выражение. Алгоритм: 1) ввести строку; 2) построить дерево; 3) вычислить выражение по дереву. Ограничения: 1) 2) 3) 4) ошибки не обрабатываем; многозначные числа не разрешены; дробные числа не разрешены; скобки не разрешены. © С. В. Кухта, 2010

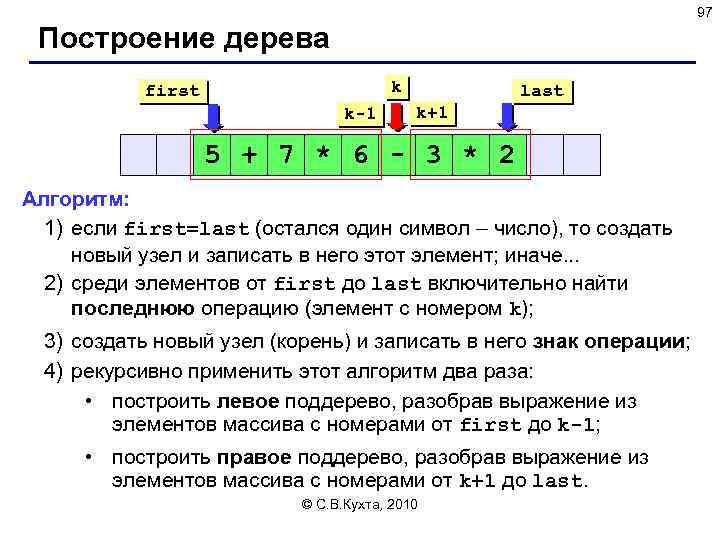97 Построение дерева k first k-1 last k+1 5 + 7 * 6 - 3 * 2 Алгоритм: 1) если first=last (остался один символ – число), то создать новый узел и записать в него этот элемент; иначе. . . 2) среди элементов от first до last включительно найти последнюю операцию (элемент с номером k); 3) создать новый узел (корень) и записать в него знак операции; 4) рекурсивно применить этот алгоритм два раза: • построить левое поддерево, разобрав выражение из элементов массива с номерами от first до k-1; • построить правое поддерево, разобрав выражение из элементов массива с номерами от k+1 до last. © С. В. Кухта, 2010

98 Как найти последнюю операцию? 5 + 7 * 6 - 3 * 2 Порядок выполнения операций • умножение и деление; • сложение и вычитание. Приоритет (старшинство) – число, определяющее последовательность выполнения операций: раньше выполняются операции с большим приоритетом: • умножение и деление (приоритет 2); • сложение и вычитание (приоритет 1). ! Нужно искать последнюю операцию с наименьшим приоритетом! © С. В. Кухта, 2010

99 Приоритет операции { Функция Priority – приоритет операции Вход: символ операции Выход: приоритет или 100, если не операция } function Priority ( c: char ): integer; begin сложение и case ( c ) of вычитание: '+', '-': Priority : = 1; приоритет 1 '*', '/': Priority : = 2; else Priority : = 100; умножение и деление: end; приоритет 2 end; это вообще не операция © С. В. Кухта, 2010

100 Номер последней операции { Функция Last. Operation – номер последней операции Вход: строка, номера первого и последнего символов рассматриваемой части Выход: номер символа - последней операции } function Last. Operation ( Expr: string; first, last: integer): integer; var Min. Prt, i, k, prt: integer; проверяем все begin Min. Prt : = 100; символы for i: =first to last do begin prt : = Priority ( Expr[i] ); if prt <= Min. Prt then begin нашли операцию с Min. Prt : = prt; минимальным k : = i; приоритетом end; вернуть номер Last. Operation : = k; символа end; © С. В. Кухта, 2010

101 Построение дерева Структура узла type PNode = ^Node; Node = record data: char; left, right: PNode; end; Создание узла для числа (без потомков) function Number. Node(c: char): PNode; begin один символ, New(Number. Node); число Number. Node^. data : = c; Number. Node^. left : = nil; возвращает адрес Number. Node^. right : = nil; созданного узла end; © С. В. Кухта, 2010

102 Построение дерева { Функция Make. Tree – построение дерева Вход: строка, номера первого и последнего символов рассматриваемой части Выход: адрес построенного дерева } function Make. Tree ( Expr: string; first, last: integer): PNode; var k: integer; осталось begin только число if first = last then begin Make. Tree : = Number. Node ( Expr[first] ); Exit; end; k : = Last. Operation ( Expr, first, last ); New(Make. Tree); новый узел: операция Make. Tree^. data : = Expr[k]; Make. Tree^. left : = Make. Tree ( Expr, first, k-1 ); Make. Tree^. right : = Make. Tree ( Expr, k+1, last ); end; © С. В. Кухта, 2010

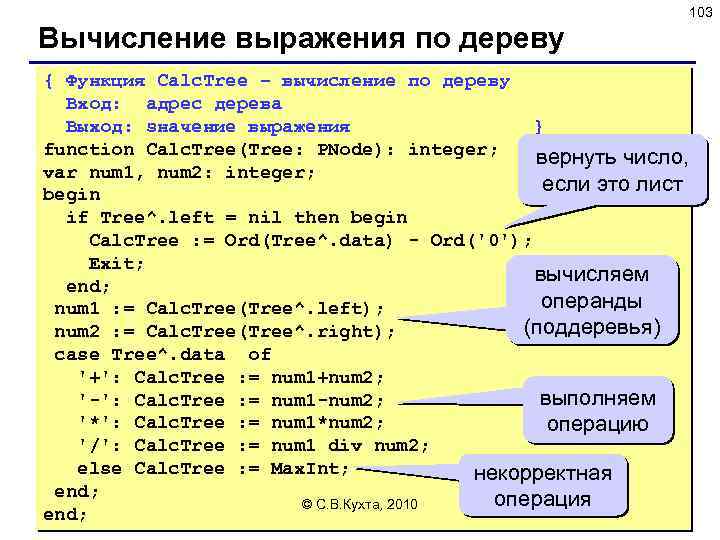103 Вычисление выражения по дереву { Функция Calc. Tree – вычисление по дереву Вход: адрес дерева Выход: значение выражения } function Calc. Tree(Tree: PNode): integer; вернуть число, var num 1, num 2: integer; если это лист begin if Tree^. left = nil then begin Calc. Tree : = Ord(Tree^. data) - Ord('0'); Exit; вычисляем end; операнды num 1 : = Calc. Tree(Tree^. left); (поддеревья) num 2 : = Calc. Tree(Tree^. right); case Tree^. data of '+': Calc. Tree : = num 1+num 2; выполняем '-': Calc. Tree : = num 1 -num 2; '*': Calc. Tree : = num 1*num 2; операцию '/': Calc. Tree : = num 1 div num 2; else Calc. Tree : = Max. Int; некорректная end; операция © С. В. Кухта, 2010 end;

104 Основная программа { Ввод и вычисление выражения с помощью дерева } program qq; var Tree: PNode; Expr: string; { процедуры и функции } begin write('Введите выражение > '); readln( Expr ); Tree : = Make. Tree( Expr, 1, Length(Expr) ); writeln(' = ', Calc. Tree(Tree) ); end. © С. В. Кухта, 2010

105 Дерево игры Задача. Перед двумя игроками лежат две кучки камней, в первой из которых 3, а во второй – 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16. Кто выигрывает при безошибочной игре – игрок, делающий первый ход, или игрок, делающий второй ход? Как должен ходить выигрывающий игрок? © С. В. Кухта, 2010

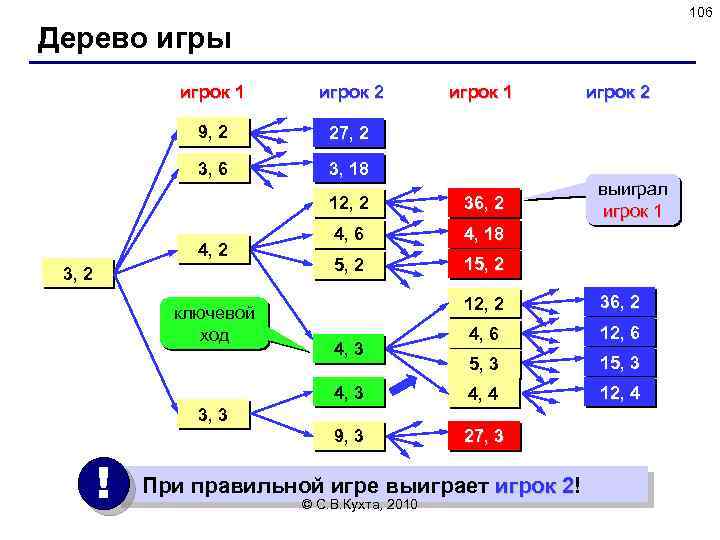106 Дерево игры игрок 1 игрок 2 9, 2 27, 2 3, 6 игрок 1 3, 18 12, 2 4, 2 36, 2 4, 6 выиграл игрок 1 4, 18 5, 2 игрок 2 15, 2 12, 2 36, 2 4, 6 12, 6 5, 3 15, 3 4, 4 12, 4 9, 3 ключевой ход 27, 3 4, 3 3, 3 ! При правильной игре выиграет игрок 2! 2 © С. В. Кухта, 2010

107 Задания « 8» : «Собрать» программу для вычисления правильного арифметического выражения, включающего только однозначные числа и знаки операций +, -, * , /. « 10» : То же самое, но допускаются также многозначные числа и скобки. « 10» : То же самое, но с обработкой ошибок (должно выводиться сообщение). © С. В. Кухта, 2010

108 13. Графы © С. В. Кухта, 2010

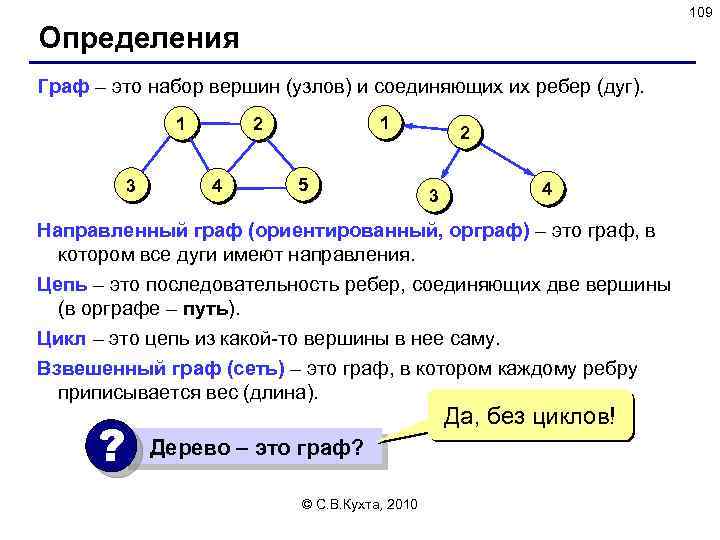109 Определения Граф – это набор вершин (узлов) и соединяющих их ребер (дуг). 1 3 1 2 4 5 2 3 4 Направленный граф (ориентированный, орграф) – это граф, в котором все дуги имеют направления. Цепь – это последовательность ребер, соединяющих две вершины (в орграфе – путь). Цикл – это цепь из какой-то вершины в нее саму. Взвешенный граф (сеть) – это граф, в котором каждому ребру приписывается вес (длина). ? Да, без циклов! Дерево – это граф? © С. В. Кухта, 2010

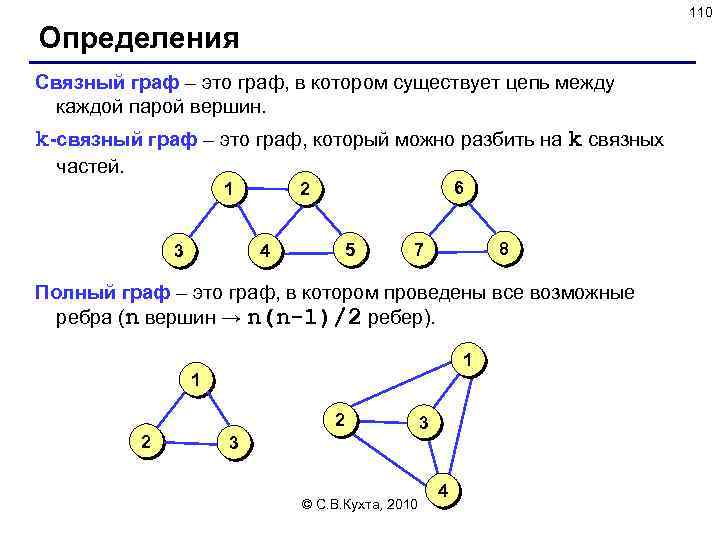110 Определения Связный граф – это граф, в котором существует цепь между каждой парой вершин. k-cвязный граф – это граф, который можно разбить на k связных частей. 1 3 6 2 5 4 8 7 Полный граф – это граф, в котором проведены все возможные ребра (n вершин → n(n-1)/2 ребер). 1 1 2 2 3 3 © С. В. Кухта, 2010 4

111 Описание графа Матрица смежности – это матрица, элемент M[i][j] которой равен 1, если существует ребро из вершины i в вершину j, и равен 0, если такого ребра нет. Список смежности 3 2 4 5 1 1 1 0 1 2 3 4 1 0 0 1 1 2 1 4 5 3 1 0 0 3 1 1 1 0 0 1 4 1 2 5 5 0 1 0 5 2 4 2 3 4 5 0 1 1 1 0 1 2 3 2 1 0 1 Симметрия! 5 1 ! 5 4 4 4 3 3 1 2 2 2 1 1 0 0 0 1 1 2 4 5 3 0 0 0 3 4 0 0 1 4 5© С. В. Кухта, 0 0 2010 0 5 5 4

112 Матрица и список смежности 1 1 2 2 3 4 5 1 2 1 3 3 4 5 4 2 4 5 3 1 5 1 2 2 3 4 5 1 2 5 3 4 1 2 3 3 4 4 5 5 © С. В. Кухта, 2010

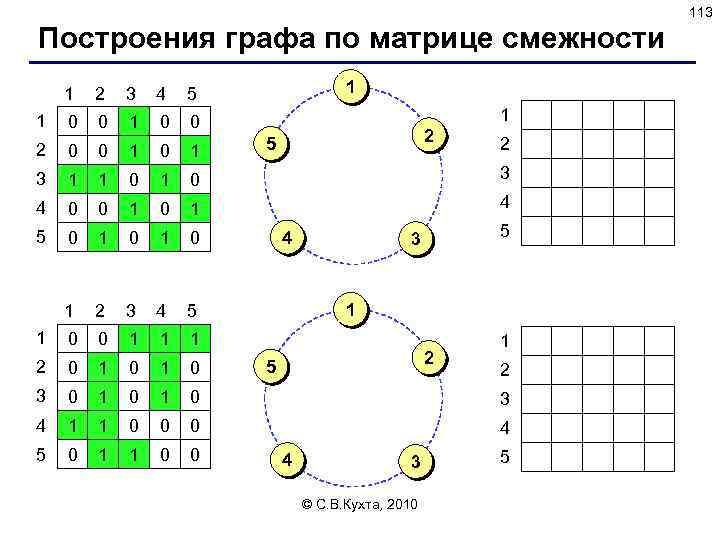113 Построения графа по матрице смежности 1 1 2 3 4 0 0 1 5 0 1 2 5 2 2 0 0 1 3 1 1 0 3 4 0 0 1 4 5 0 1 0 1 2 3 4 5 1 0 0 1 1 1 2 0 1 0 1 0 3 4 1 1 0 0 0 4 5 0 1 1 0 0 4 5 3 1 2 5 4 3 © С. В. Кухта, 2010 1 2 5

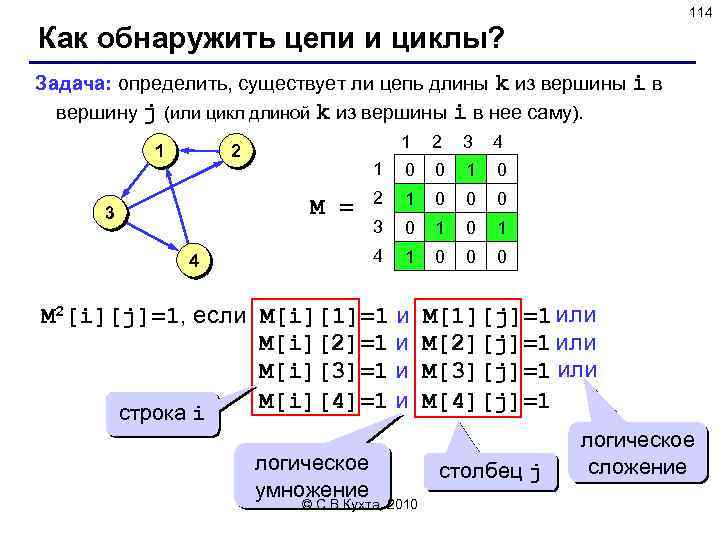114 Как обнаружить цепи и циклы? Задача: определить, существует ли цепь длины k из вершины i в вершину j (или цикл длиной k из вершины i в нее саму). 1 1 4 3 4 0 0 1 0 2 1 0 0 0 3 0 1 4 M = 3 2 1 0 0 0 M 2[i][j]=1, если M[i][1]=1 и M[i][2]=1 и M[i][3]=1 и M[i][4]=1 и строка i логическое умножение © С. В. Кухта, 2010 M[1][j]=1 или M[2][j]=1 или M[3][j]=1 или M[4][j]=1 столбец j логическое сложение

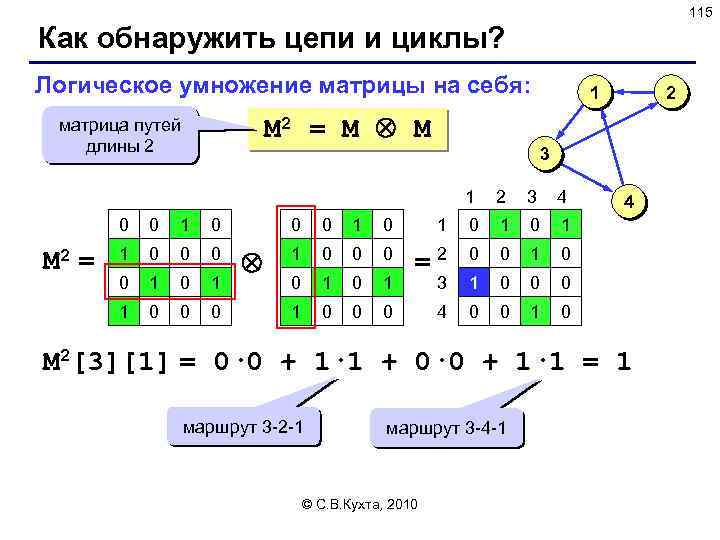115 Как обнаружить цепи и циклы? Логическое умножение матрицы на себя: M 2 = M M матрица путей длины 2 1 3 1 2 3 4 0 0 1 0 1 0 1 0 0 0 0 0 1 0 1 0 1 =2 3 1 0 0 0 4 0 0 1 4 1 1 M 2 = 2 0 M 2[3][1] = 0· 0 + 1· 1 + 0· 0 + 1· 1 = 1 маршрут 3 -2 -1 маршрут 3 -4 -1 © С. В. Кухта, 2010

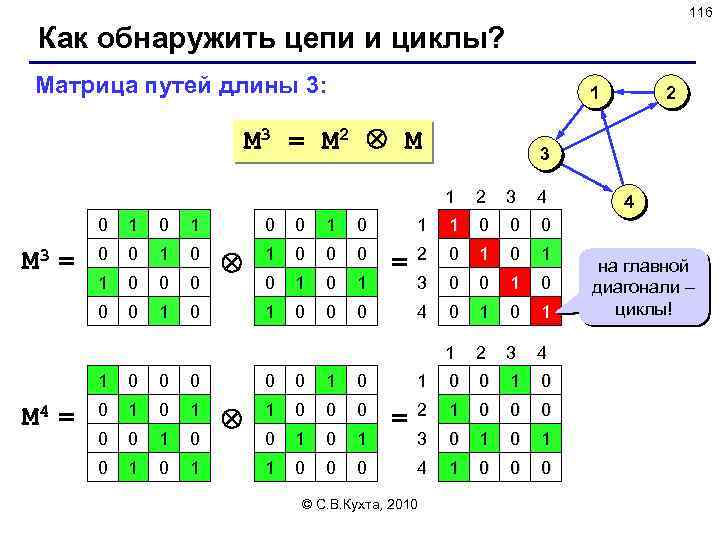116 Как обнаружить цепи и циклы? Матрица путей длины 3: 1 M 3 = M 2 M 3 1 0 0 1 0 1 0 0 1 M 4 = 0 0 0 1 0 1 1 0 0 0 1 0 1 0 1 1 0 0 0 = 1 0 0 0 2 0 1 3 0 0 1 0 1 2 3 4 1 0 4 4 0 = 3 1 0 0 M 3 = 1 2 1 0 2 0 0 1 0 2 1 0 0 0 3 0 1 4 1 0 0 0 © С. В. Кухта, 2010 4 на главной диагонали – циклы!

117 Весовая матрица – это матрица, элемент W[i, j] которой равен весу ребра из вершины i в вершину j (если оно есть), или равен ∞, если такого ребра нет. 7 1 3 5 3 2 3 8 4 4 7 1 5 6 1 2 3 4 1 0 7 3 5 ∞ 2 7 0 ∞ 4 3 8 4 5 3 5 2 4 5 6 1 2 3 4 5 1 0 7 3 5 ∞ 8 2 ∞ 0 ∞ 4 8 3 ∞ 0 ∞ ∞ 3 3 ∞ 0 ∞ ∞ 4 5 4 ∞ 0 6 4 5 ∞ ∞ 0 5 ∞ 8 ∞ 6 0 5 ∞ 8 ∞ ∞ 0 © С. В. Кухта, 2010 6

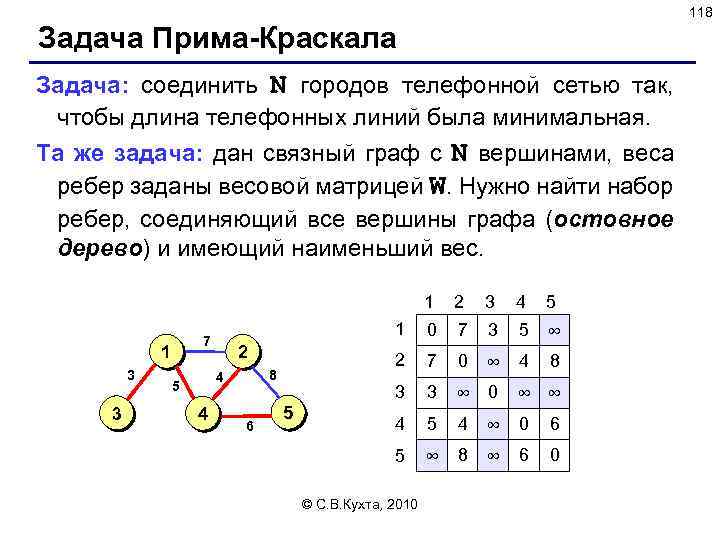118 Задача Прима-Краскала Задача: соединить N городов телефонной сетью так, чтобы длина телефонных линий была минимальная. Та же задача: дан связный граф с N вершинами, веса ребер заданы весовой матрицей W. Нужно найти набор ребер, соединяющий все вершины графа (остовное дерево) и имеющий наименьший вес. 1 1 3 3 4 6 5 5 0 7 3 5 ∞ 7 0 ∞ 4 8 3 8 4 5 4 2 2 3 1 7 2 3 ∞ 0 ∞ ∞ 4 5 4 ∞ 0 6 5 ∞ 8 ∞ 6 0 © С. В. Кухта, 2010

119 Жадный алгоритм – это многошаговый алгоритм, в котором на каждом шаге принимается решение, лучшее в данный момент. ! В целом может получиться не оптимальное решение (последовательность шагов)! Шаг в задаче Прима-Краскала – это выбор еще невыбранного ребра и добавление его к решению. 7 1 3 3 8 4 5 4 ! 2 6 5 В задаче Прима-Краскала жадный алгоритм дает оптимальное решение! © С. В. Кухта, 2010

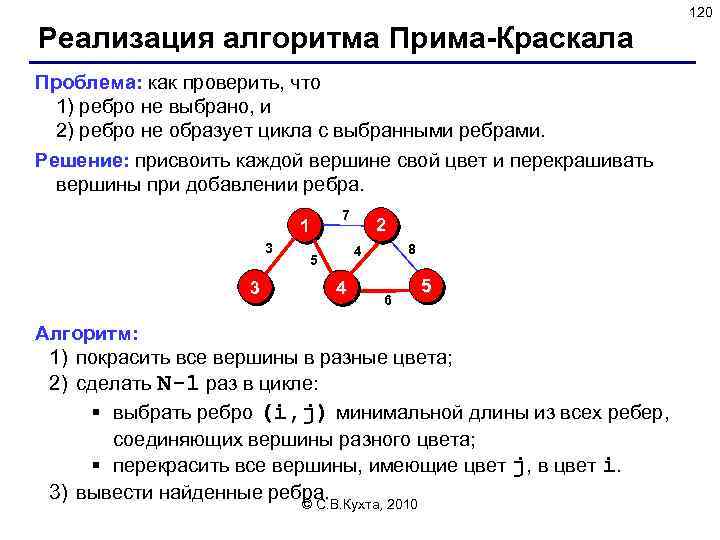120 Реализация алгоритма Прима-Краскала Проблема: как проверить, что 1) ребро не выбрано, и 2) ребро не образует цикла с выбранными ребрами. Решение: присвоить каждой вершине свой цвет и перекрашивать вершины при добавлении ребра. 1 3 3 7 2 8 4 5 4 6 5 Алгоритм: 1) покрасить все вершины в разные цвета; 2) сделать N-1 раз в цикле: § выбрать ребро (i, j) минимальной длины из всех ребер, соединяющих вершины разного цвета; § перекрасить все вершины, имеющие цвет j, в цвет i. 3) вывести найденные ребра. © С. В. Кухта, 2010

121 Реализация алгоритма Прима-Краскала Структура «ребро» : type rebro = record i, j: integer; { номера вершин } end; Основная программа: весовая матрица const N = 5; цвета var W: array[1. . N, 1. . N] of integer; вершин Color: array[1. . N] of integer; i, j, k, min, col_i, col_j: integer; Reb: array[1. . N-1] of rebro; begin. . . { здесь надо ввести матрицу W } for i: =1 to N do { раскрасить в разные цвета } Color[i] : = i; . . . { основной алгоритм – заполнение массива Reb }. . . { вывести найденные ребра (массив Reb)} end. © С. В. Кухта, 2010

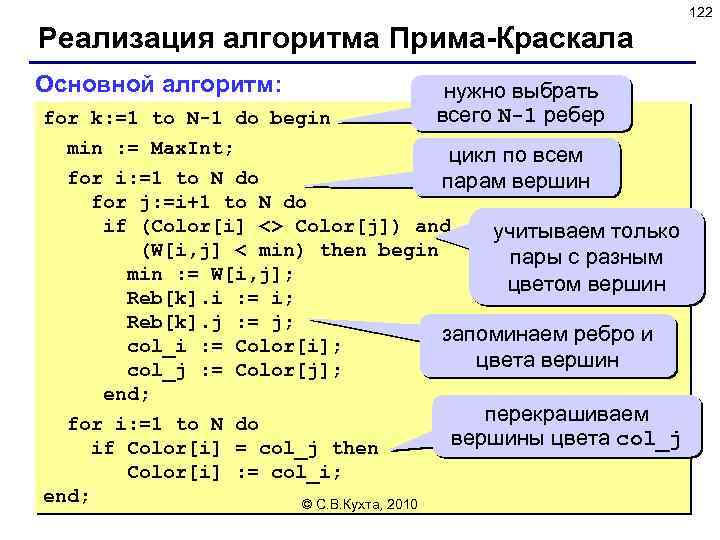122 Реализация алгоритма Прима-Краскала Основной алгоритм: нужно выбрать всего N-1 ребер for k: =1 to N-1 do begin min : = Max. Int; цикл по всем for i: =1 to N do парам вершин for j: =i+1 to N do if (Color[i] <> Color[j]) and учитываем только (W[i, j] < min) then begin пары с разным min : = W[i, j]; цветом вершин Reb[k]. i : = i; Reb[k]. j : = j; запоминаем ребро и col_i : = Color[i]; цвета вершин col_j : = Color[j]; end; перекрашиваем for i: =1 to N do вершины цвета col_j if Color[i] = col_j then Color[i] : = col_i; end; © С. В. Кухта, 2010

123 Сложность алгоритма Основной цикл: for k: =1 to N-1 do begin. . . for i: =1 to N do for j: =i+1 to N do. . . три вложенных цикла, в каждом число шагов <=N end; Количество операций: O(N 3) растет не быстрее, чем N 3 Требуемая память: var W: array[1. . N, 1. . N] of integer; Color: array[1. . N] of integer; Reb: array[1. . N-1] of rebro; © С. В. Кухта, 2010 O(N 2)

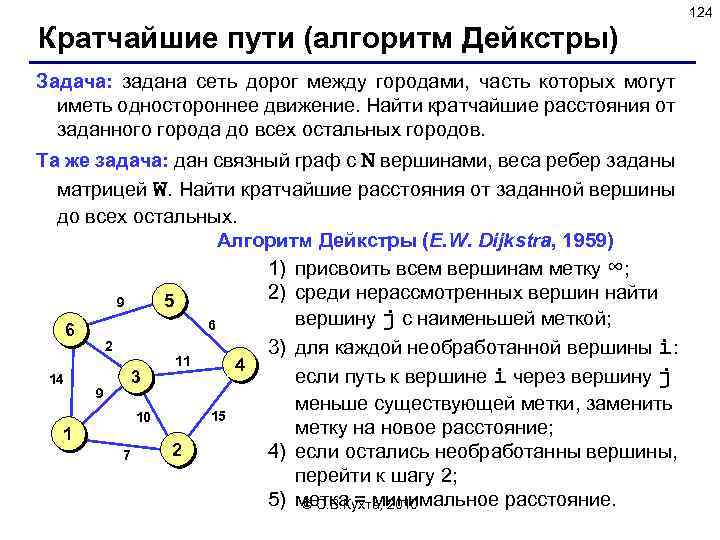124 Кратчайшие пути (алгоритм Дейкстры) Задача: задана сеть дорог между городами, часть которых могут иметь одностороннее движение. Найти кратчайшие расстояния от заданного города до всех остальных городов. Та же задача: дан связный граф с N вершинами, веса ребер заданы матрицей W. Найти кратчайшие расстояния от заданной вершины до всех остальных. Алгоритм Дейкстры (E. W. Dijkstra, 1959) 1) присвоить всем вершинам метку ∞; 2) среди нерассмотренных вершин найти 9 5 вершину j с наименьшей меткой; 6 6 2 3) для каждой необработанной вершины i: 11 4 если путь к вершине i через вершину j 3 14 9 меньше существующей метки, заменить 15 10 метку на новое расстояние; 1 2 4) если остались необработанны вершины, 7 перейти к шагу 2; 5) метка = минимальное расстояние. © С. В. Кухта, 2010

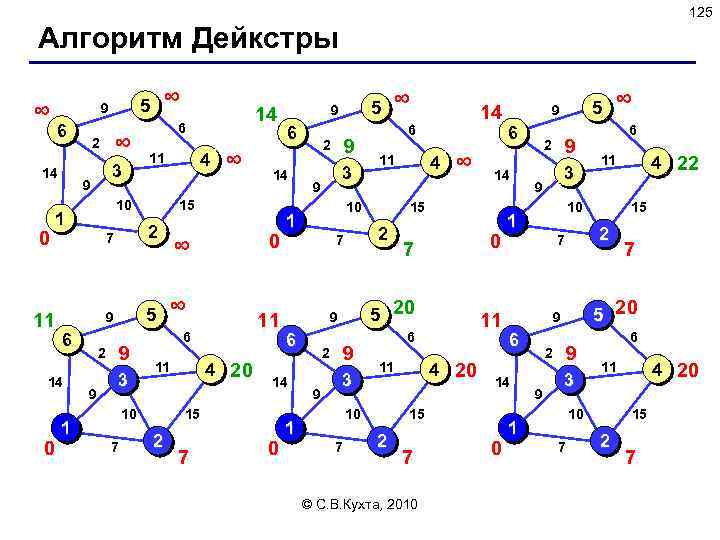125 Алгоритм Дейкстры ∞ 6 14 0 ∞ 3 9 2 5 9 3 7 ∞ 11 4 20 11 2 7 6 0 9 2 3 9 ∞ 15 9 3 7 0 11 6 7 2 7 © С. В. Кухта, 2010 6 0 9 2 3 9 ∞ 6 15 2 7 2 9 7 5 20 9 6 4 22 11 10 1 14 15 10 1 4 20 11 5 9 14 5 20 9 2 4 11 2 7 6 14 6 10 1 14 15 5 9 14 0 ∞ 6 10 1 ∞ 15 9 14 4 11 7 6 14 6 10 1 11 0 2 ∞ 5 9 9 3 6 15 10 1 7 4 20 11 2 7

126 Реализация алгоритма Дейкстры Массивы: 1) массив a, такой что a[i]=1, если вершина уже рассмотрена, и a[i]=0, если нет. 2) массив b, такой что b[i] – длина текущего кратчайшего пути из заданной вершины x в вершину i; 3) массив c, такой что c[i] – номер вершины, из которой нужно идти в вершину i в текущем кратчайшем пути. Инициализация: 1) заполнить массив a нулями (вершины не обработаны); 2) записать в b[i] значение W[x][i]; 3) заполнить массив c значением x; 4) записать a[x]=1. 14 6 14 0 5 9 2 9 9 3 7 1 6 4 11 15 10 1 ∞ 2 7 ∞ 2 3 4 5 6 a 1 0 0 0 b 0 7 9 ∞ ∞ 14 c 0 0 0 © С. В. Кухта, 2010

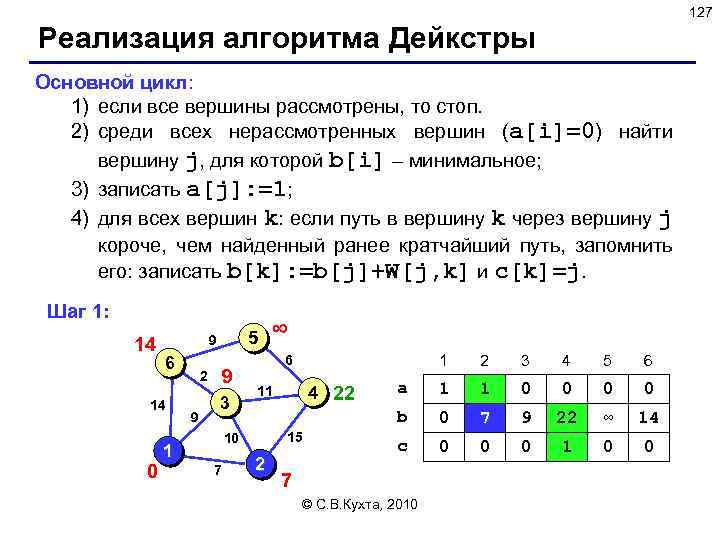127 Реализация алгоритма Дейкстры Основной цикл: 1) если все вершины рассмотрены, то стоп. 2) среди всех нерассмотренных вершин (a[i]=0) найти вершину j, для которой b[i] – минимальное; 3) записать a[j]: =1; 4) для всех вершин k: если путь в вершину k через вершину j короче, чем найденный ранее кратчайший путь, запомнить его: записать b[k]: =b[j]+W[j, k] и c[k]=j. Шаг 1: 14 6 14 0 5 9 2 9 9 3 7 1 2 3 4 5 6 a 1 1 0 0 b 0 7 9 22 ∞ 14 c 0 0 0 1 0 0 6 4 22 11 15 10 1 ∞ 2 7 © С. В. Кухта, 2010

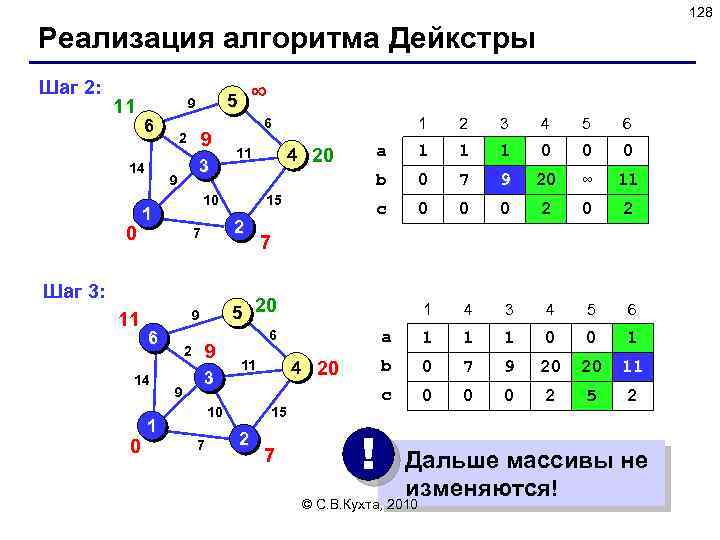128 Реализация алгоритма Дейкстры Шаг 2: 11 6 14 0 9 2 3 9 1 14 0 9 3 4 5 6 1 1 1 0 0 0 b 0 7 9 20 ∞ 11 c 0 0 0 2 1 4 3 4 5 6 a 1 1 1 0 0 1 b 0 7 9 20 20 11 c 15 2 9 2 2 a 4 20 11 7 6 1 0 0 0 2 5 2 6 10 5 20 Шаг 3: 11 ∞ 5 9 9 3 6 7 4 20 11 15 10 1 7 2 7 ! Дальше массивы не изменяются! © С. В. Кухта, 2010

129 Как вывести маршрут? Результат работа алгоритма Дейкстры: 1 2 3 4 5 6 a 1 1 1 b 0 7 9 20 20 11 c 0 0 0 2 5 2 длины путей Маршрут из вершины 0 в вершину 4: 4 5 2 0 Вывод маршрута в вершину i (использование массива c): 1) установить z: =i; 2) пока c[i]<>x присвоить z: =c[z] и вывести z. Сложность алгоритма Дейкстры: два вложенных цикла по N шагов O(N 2) © С. В. Кухта, 2010

130 Алгоритм Флойда-Уоршелла Задача: задана сеть дорог между городами, часть которых могут иметь одностороннее движение. Найти все кратчайшие расстояния, от каждого города до всех остальных городов. for k: =1 to N for i: = 1 to N for j: = 1 to N if W[i, j] > W[i, k] + W[k, j] then W[i, j] : = W[i, k] + W[k, j]; k W[i, k] i W[i, j] ! W[k, j] j Если из вершины i в вершину j короче ехать через вершину k, мы едем через вершину k! Нет информации о маршруте, только кратчайшие расстояния! © С. В. Кухта, 2010

131 Алгоритм Флойда-Уоршелла Версия с запоминанием маршрута: for i: = 1 to N i–ая строка строится так for j : = 1 to N же, как массив c в c[i, j] : = i; алгоритме Дейкстры . . . for k: =1 to N for i: = 1 to N for j: = 1 to N if W[i, j] > W[i, k] + W[k, j] then begin W[i, j] : = W[i, k] + W[k, j]; c[i, j] : = c[k, j]; end; ? в конце цикла c[i, j] – Какова сложность предпоследняя вершина в алгоритма? кратчайшем маршруте из O(N 3) вершины i в вершину j© С. В. Кухта, 2010

132 Задача коммивояжера. Коммивояжер (бродячий торговец) должен выйти из первого города и, посетив по разу в неизвестном порядке города 2, 3, . . . N, вернуться обратно в первый город. В каком порядке надо обходить города, чтобы замкнутый путь (тур) коммивояжера был кратчайшим? ! Это NP-полная задача, которая строго решается только перебором вариантов (пока)! Точные методы: большое время счета для 1) простой перебор; больших N 2) метод ветвей и границ; O(N!) 3) метод Литтла; 4) … Приближенные методы: не гарантируется 1) метод случайных перестановок (Matlab); оптимальное 2) генетические алгоритмы; решение 3) метод муравьиных колоний; © С. В. Кухта, 2010 4) …

133 Другие классические задачи Задача на минимум суммы. Имеется N населенных пунктов, в каждом из которых живет pi школьников (i=1, . . . , N). Надо разместить школу в одном из них так, чтобы общее расстояние, проходимое всеми учениками по дороге в школу, было минимальным. Задача о наибольшем потоке. Есть система труб, которые имеют соединения в N узлах. Один узел S является источником, еще один – стоком T. Известны пропускные способности каждой трубы. Надо найти наибольший поток от источника к стоку. Задача о наибольшем паросочетании. Есть M мужчин и N женщин. Каждый мужчина указывает несколько (от 0 до N) женщин, на которых он согласен жениться. Каждая женщина указывает несколько мужчин (от 0 до M), за которых она согласна выйти замуж. Требуется заключить наибольшее количество моногамных браков. © С. В. Кухта, 2010