8_ukr.ppt
- Количество слайдов: 39

Тема 8 ЖАДІБНІ АЛГОРИТМИ, ТЕОРЕТИЧНІ ОСНОВИ, ЗАСТОСУВАННЯ Дайте мені таблеток від жадібності й побільше, побільше. . . ( Народний фольклор )

8. 1 Вступ • У теорії алгоритмів відіграють важливу роль жадібні алгоритми. Вони прості для розуміння й реалізації, працюють порівняно швидко, відомо багато різноманітних завдань, які можна вирішити за допомогою таких алгоритмів. Однак не завжди можна довести можливість застосовності жадібного алгоритму для знаходження точного рішення багатьох завдань.

8. 1 Вступ • Жадібний алгоритм (greedy algorithm) - метод рішення оптимізаційних задач, заснований на тому, що процес прийняття рішення можна розбити на елементарні кроки, на кожному з яких приймається окреме рішення. Рішення, прийняте на кожному кроці, повинно бути оптимальним тільки на поточному кроці й повинно прийматися без обліку попередніх або наступних рішень.

8. 1 Вступ • Алгоритми, призначені для рішення задач оптимізації, звичайно являють собою послідовність кроків, на кожному з яких надається деяка множина виборів. Визначення найкращого вибору, керуючись засадами динамічного програмування, у багатьох задач оптимізації нагадує стрілянину з гармати по горобцях; інакше кажучи, для цих завдань краще підходять більше прості й ефективні алгоритми. У жадібному алгоритмі завжди робиться вибір, що здається найкращим у цей момент - тобто виробляється локально оптимальний вибір у надії, що він приведе до оптимального рішення глобального завдання. Жадібні алгоритми не завжди приводять до оптимального рішення, але в багатьох завданнях вони дають потрібний результат. Жадібний алгоритм має достатню міць і добре підходить для широкого класу завдань. Алгоритми пошуку мінімальних остовних дерев являють класичний приклад застосування жадібного методу.

8. 1 Вступ • Ознаки того, що задачу можливо вирішити за допомогою жадібного алгоритму: 1 задачу можна розбити на підзадачі; • 2 величини, розглянуті в задачі, можна дробити так само на підзадачі; • 3 сума оптимальних рішень для двох підзадач дасть оптимальне рішення для всього завдання. • Приклад 8. 1 Пасажирський ліфт не може підняти більше W кг. У ліфт намагаються влізти H чоловіків, причому кожного з них відома вага: W 1, W 2. . . WH. Визначити яка максимальна кількість людей зможе виїхати на ліфті за один раз. • Рішення. Очевидно, що елементарної підзадачою є поміщення в ліфт однієї людини. Якщо є декілька кандидатів в ліфт, то оптимальним вибором буде людина з найменшою вагою, тому що при цьому залишається найбільший запас по вантажопідйомності. Тому, для рішення завдання, відсортуємо людей по їхній вазі й будемо, починаючи із самої найлегшої, поміщати їх у ліфт, поки це ще можна зробити.

8. 1 Вступ • Приклад 8. 2 Завдання про вибір заявок • Дано n заявок на проведення занять у деякій аудиторії. У кожній заявці зазначені початок і кінець заняття (si і fi для i-й заявки). Два різних заняття не можуть перекриватися за часом. Заявки з номерами i і j сумісні, якщо інтервали [si, fi) і [sj, fj) не перетинаються (тобто fi ≤ sj або fj ≤ si). Завдання про вибір заявок полягає в тому, щоб набрати максимальна кількість заявок. • Рішення. Приведемо жадібний алгоритм, що вирішує дане завдання. При цьому думаємо, що заявки впорядковані в порядку зростання часу закінчення.

8. 1 Вступ • Рішення. Приведемо жадібний алгоритм, що вирішує дане завдання. При цьому думаємо, що заявки впорядковані в порядку зростання часу закінчення. • Activity-Selector(s, f) • 1 n ← length[s] • 2 A ← {а 1} • 3 i ← 1 • 4 for m ← 2 to n • 5 do if sm ≥ fj • 6 then A ← A {аm} • 7 i ← m • 8 return A

8. 1 Вступ • • • Recursive_Activity_Selektor (S, f, i, n) 1 m←i+1 2 while m≤n і sm<fi 3 do m ←m+1 4 if m≤n 5 them return {am} Recursive_Activity_Selektor (S, f, i, n) • 6 else return Ǿ

8. 1 Вступ

8. 1 Вступ • Процедура працює в такий спосіб. Змінна i індексує саме останнє додавання до множини A, що відповідає процесу ai у рекурсивній версії. • У рядках 2– 3 вибирається процес a 1, ініціалізуєься множиною A, що містить тільки цей процес, а змінної i привласнюється індекс цього процесу. У циклі for у рядках 4 – 7 відбувається пошук процесу завдання Si, n+1, що кінчається раніше інших. У цьому циклі по черзі розглядається кожний процес aj який додається до множини A, якщо він сумісний з усіма раніше обраними процесами; цей процес кінчається раніше інших у завданні Si, n+1. Щоб довідатися, чи сполучимо процес aj із процесами, які вже втримуються в множині A, досить перевірити (рядок 5), що його початковий момент sj наступає не раніше моменту fi закінчення останнього з доданих у множину A процесів. Якщо процес aj задовольняє сформульованим вище умовам, то в рядках 6– 7 він додається в множину A і змінної i привласнюється значення j. • Алгоритм працює за O(nlog 2 n+n), тобто сортування плюс вибірка. На кожному кроці вибирається найкраще рішення.

8. 1 Вступ • Теорема 8. 1 Алгоритм Activity-Selector(s, f) дає набір з найбільшої можливої кількості спільних заявок. Доказ. Помітимо, що всі заявки відсортовані по зростанню часу закінчення. Заявка номер 1, мабуть, входить в оптимум (якщо ні, те замінимо саму ранню заявку в оптимумі на неї, від цього гірше не стане). Викинувши всі заявки, не спільні з першої, одержимо вихідне завдання з меншою кількістю заявок. Міркуючи по індукції, аналогічним образом приходимо до оптимального рішення.

8. 2 Застосовність жадібного алгоритму • У загальному випадку не можна сказати, чи можна одержати оптимальне рішення за допомогою жадібного алгоритму стосовно до конкретного завдання. Але є дві особливості, характерні для завдань, які вирішуються за допомогою жадібних алгоритмів: принцип жадібного вибору й властивість оптимальності для підзадач.

8. 2 Застосовність жадібного алгоритму • А Принцип жадібного вибору • Говорять, що до завдання оптимізації застосуємо принцип жадібного вибору, якщо послідовність локально оптимальних виборів дає глобально оптимальне рішення. У цьому складається головна відмінність жадібних алгоритмів від динамічного програмування: у другому прораховуються відразу наслідки всіх варіантів. Щоб довести, що жадібний алгоритм дає оптимум, потрібно спробувати провести доказ, аналогічний доказу алгоритму завдання про вибір заявок. Спочатку ми показуємо, що жадібний вибір на першому кроці не закриває шлях до оптимального рішення: для будь-якого рішення є інше, погоджене з жадібним вибором і не гірше першого. Потім ми показуємо, що підзадача, що виникла після жадібного вибору на першому кроці, аналогічна вихідної. По індукції буде випливати, що така послідовність жадібних виборів дає оптимальне рішення.

8. 2 Застосовність жадібного алгоритму • Б Оптимальність для підзадач • Ця властивість говорить про те, що оптимальне рішення всього завдання містить у собі оптимальні рішення підзадач. Наприклад, у завданні про вибір заявок можна помітити, що якщо A - оптимальний набір заявок, що містить заявку номер 1, то A′ = A {1} — оптимальний набір заявок для меншої множини заявок S′, що складається з тих заявок, для яких si ≥ f 1.

8. 2 Застосовність жадібного алгоритму • Жадібний алгоритм або динамічне програмування? • Розходження між динамічним програмуванням і жадібним алгоритмом можна проілюструвати на прикладі завдання про рюкзак, а точніше, на її дискретному й безперервному формулюванні. Далі ми покажемо, що безперервне завдання вирішується жадібним методом, дискретна ж вимагає більше тонкого, динамічного рішення.

8. 2 Застосовність жадібного алгоритму • Приклад 8. 3 Дискретне завдання про рюкзак. Злодій пробрався на склад, на якому зберігається n речей. Кожна річ коштує vi доларів і важить wi кілограм. Злодій хоче віднести товару на максимальну суму, однак він не може підняти більше W кілограм (всі числа цілі). Що він повинен покласти в рюкзак? • Приклад 8. 4 Безперервне завдання про рюкзак. Тепер злодій уміє дробити товари й укладати в рюкзак тільки їхньої частини, а не обов'язково цілком. Звичайно в дискретному завданні мова йде про золоті злитки різної проби, а в безперервної - про золотий пісок.

8. 2 Застосовність жадібного алгоритму

8. 2 Застосовність жадібного алгоритму • Рішення. Маючи порожній рюкзак вантажопідйомністю 50 кг, у випадку безперервного завдання розраховуємо питому вартість речей, потім беремо по максимуму найдорожчої речі, потім другий за вартістю й т. д. доти, поки останню річ не прийде розділити. У випадку ж дискретного завдання, користуючись тими ж міркуваннями, ми покладемо спочатку першу річ, однак тепер нам набагато вигідніше укласти рюкзак «під зав'язку» не найдорожчими (розраховуючи на кілограм) предметами, як показано на малюнку. Так ми заробимо $220 замість одержуваних по алгоритму $160.

8. 3 Коди Хаффмена • Коди Хаффмена (Huffman codes) широко використовуються при стиску інформації. Ці коди можна побудувати за допомогою жадібного алгоритму, що був запропонований Хаффменом. • Коди Хаффмана (Huffman codes) - широко розповсюджений і дуже ефективний метод стиску даних, що, залежно від характеристик цих даних, звичайно дозволяє заощадити від 20% до 90% обсягу. Ми розглядаємо дані, що представляють собою послідовність символів. У жадібному алгоритмі Хаффмана використовується таблиця, що містить частоти появи тих або інших символів. За допомогою цієї таблиці визначається оптимальне подання кожного символу у вигляді бінарного рядка. Припустимо, що є файл даних, що складає з 100 000 символів, що потрібно стиснути. Символи в цьому файлі зустрічаються із частотою, представленої в табл. 8. 1. Таким чином, усього файл містить шість різних символів, а, наприклад, символ a зустрічається в ньому 45 000 разів.

8. 3 Коди Хаффмена

8. 3 Коди Хаффмена • Існує безліч способів представити подібний файл даних. Розглянемо завдання по розробці бінарного коду символів (binary character code; або для стислості просто коду), у якому кожний символ представляється унікальним бінарним рядком. Якщо використовується код фіксованої довжини, або рівномірний код ( xed-length code), то для подання шести символів знадобиться 3 битка: a = 000, b = 001, . . . , f = 101. При використанні такого методу для кодування всього файлу знадобиться 300 000 битов. Чи можна домогтися • кращих результатів?

8. 3 Коди Хаффмена • За допомогою коду змінної довжини, або нерівномірного коду (variablelength code), вдається одержати значно кращі результати, чим за допомогою коду фіксованої довжини. Це досягається за рахунок того, що часто, що зустрічаються символам, зіставляються короткі кодові слова, а рідко зустрічається - довгі. Такий код представлений в останньому рядку табл. 8. 1. У ньому символ a представлений 1 -бітовим рядком 0, а символ f — 4 -бітовим рядком 1100. Для подання файлу за допомогою цього коду буде потрібно (45 · 1 + 13 · 3 + 12 · 3 + 16 · 3 + 9 · 4 + 5 4) · 1000 = 224 000 битов. • Завдяки цьому додатково заощаджується 25% обсягу.

8. 3 Коди Хаффмена • Далі ми розглядаємо тільки коди, у яких із двох послідовностей бітів, що представляють різні символи, жодна не є префіксом іншої — префіксні коди. Можна показати (хоча тут ми не станемо цього робити), що оптимальний стиск даних, якого можна досягти за допомогою кодів, завжди досяжно при використанні префіксного коду, тому розгляд одних лише префіксних кодів не приводить до втрати спільності. • Для будь-якого бінарного коду символів кодування тексту - дуже простий процес: треба просто з'єднати кодові слова, що представляють кожний символ у файлі. Наприклад, у кодуванні за допомогою префіксного коду змінної довжини, представленого в табл. 8. 1, трисимвольний файл abc має вигляд 0 · 101 · 100 = 0101100, де символом “·” позначена операція конкатенації.

8. 3 Коди Хаффмена • Перевага префіксним кодам віддається через те, що вони спрощують декодування. Оскільки ніяке кодове слово не виступає в ролі префікса іншого, кодове слово, з якого починається закодований файл, визначається однозначно. Початкове кодове слово легко ідентифікувати, перетворити його у вихідний символ і продовжити декодування частини, що залишилася, закодованого файлу. У розглянутому прикладі рядок 001011101 однозначно розкладається на підстроки 0 · 101 · 1101, що декодується як aabe.

8. 3 Коди Хаффмена • Для спрощення процесу декодування потрібне зручне подання префіксного коду, щоб кодове слово можна було легко ідентифікувати. Одним з таких подань є бінарне дерево, листами якого є кодуємі символи. Бінарне кодове слово, що представляє символ, інтерпретується як шлях від кореня до цього символу. У такій інтерпретації 0 означає “перейти до лівого дочірнього вузла”, а 1 — “перейти до правого дочірнього вузла”. На мал. 8. 1 показані такі дерева для двох кодів, узятих з нашого приклада. Кожний аркуш на малюнку позначений відповідної йому символом і частотою появи, а внутрішній вузол — сумою частот листів його піддерева. У частині а малюнка наведене дерево, що відповідає коду фіксованої довжини, де a = 000, . . . , f = 101. У частині б показане дерево, що відповідає оптимальному префіксному коду a = 0, b = 101, . . . , f = 1100. Помітимо, що зображені на малюнку дерева не є бінарними деревами пошуку, оскільки листи в них не обов'язково розташовані в порядку сортування, а внутрішні вузли не містять ключів символів.
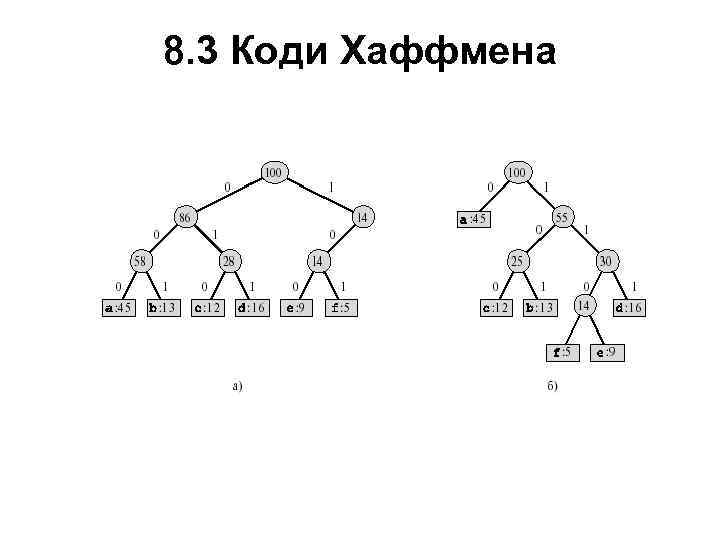
8. 3 Коди Хаффмена

8. 3 Коди Хаффмена • Оптимальний код файлу завжди може бути представлений повним бінарним деревом, у якому в кожного вузла (крім листів) є по двох дочірніх вузла. • Код фіксованої довжини, представлений у розглянутому прикладі, не є оптимальним, оскільки відповідне йому дерево, зображене на мал. 8. 1 а, — неповне бінарне дерево: деякі слова коду починаються з 10. . . , але жодне з них не починається з 11. . Оскільки в нашім обговоренні ми можемо обмежитися тільки повними бінарними деревами, можна затверджувати, що якщо C — алфавіт, з якого витягають кодуємі символи, і всі частоти, з якими зустрічаються символи, позитивні, то дерево, що представляє оптимальний префіксний код, містить рівно |C| листів, по одному для кожного символу з множини C, і рівно |C| - 1 внутрішніх вузлів.

8. 3 Коди Хаффмена • Досить легко знайти кількість бітів, необхідну для кодування файлу, якщо ми знаємо дерево T, що відповідає префіксному коду. Нехай f[c] позначає число входжень символу c з алфавіту C у файл, d(c) - глибину відповідного аркуша в дереві (довжину послідовності бітів, що кодує c). Одержуємо, що для кодування файлу необхідно бітів. • Назвемо це число вартістю дерева T.

8. 3 Коди Хаффмена • Побудова коду Хаффмена • Приведемо жадібний алгоритм Хаффмена, що будує оптимальний префіксний код — код Хаффмена. При цьому припускаємо, що для будь-якого символу c C задана його частота f[c]. В алгоритмі будується дерево T, що відповідає оптимальному коду, причому побудова йде у висхідному напрямку. Процес побудови починається з множини, що складає з |C| листів, після чого послідовно виконується |C| - 1 операцій “злиття”, у результаті яких утвориться кінцеве дерево. Для ідентифікації двох найменш що часто зустрічаються об'єктів, що підлягають злиттю, використовується черга із пріоритетами Q, ключами в якій є частоти f. У результаті злиття двох об'єктів утвориться новий об'єкт, частота появи якого є сумою частот об'єднаних об'єктів:

8. 3 Коди Хаффмена • • • Huffman(C) 1 n ← |C| 2 Q ← C 3 for i ← 1 to n – 1 4 do z ← Allocate-Node() 5 x ← left[z] ← Extract-Min(Q) 6 y ← right[z] ← Extract-Min(Q) 7 f[z] ← f[x] + f[y] 8 Insert(Q, z) 9 return Extract-Min(Q)

8. 3 Коди Хаффмена • Для розглянутого раніше прикладу алгоритм Хаффмана виводить результат, наведений на мал. 8. 2. На кожному етапі показана черга, елементи якої розсортовані в порядку зростання їхніх частот. На кожному кроці роботи алгоритму поєднуються два об'єкти (дерева) з найнижчими частотами. Листи зображені у вигляді прямокутників, у кожному з яких зазначена буква й відповідна їй частота. Внутрішні вузли представлені колами, що містять суму частот дочірніх вузлів. Ребро, що з'єднує внутрішній вузол з лівим дочірнім вузлом, має мітку 0, а ребро, що з'єднує його із правим дочірнім вузлом, — мітку 1. Слово для букви утвориться послідовністю міток на ребрах, що з'єднують корінь із листком, що представляє цю букву. Оскільки дана множина містить шість букв, розмір вихідної черги дорівнює 6 (частина а малюнка), а для побудови дерева потрібно п'ять злиттів. Проміжні етапи зображені в частинах б-д. Кінцеве дерево (мал. 8. 2 е) представляє оптимальний префіксний код. Як уже говорилося, слово коду для букви - це послідовність міток на шляху від кореня до листка із цією
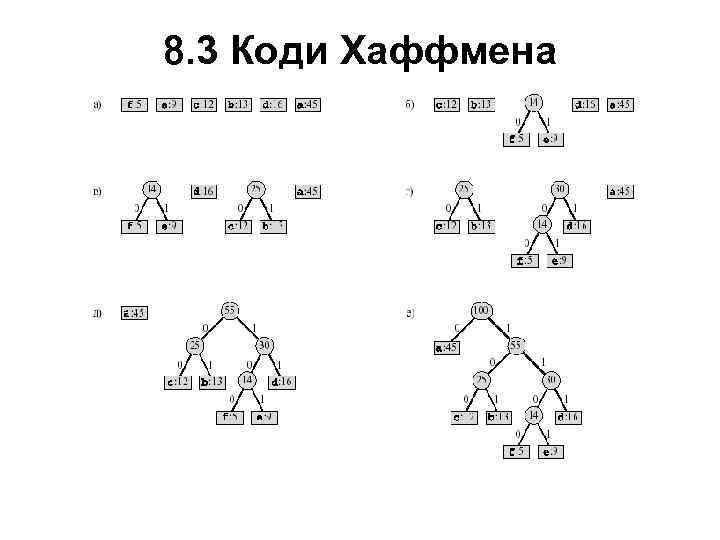
8. 3 Коди Хаффмена

8. 3 Коди Хаффмена • У рядку 2 ініціалізується черга із пріоритетами Q, що складається з елементів множини C. Цикл for у рядках 3– 8 по черзі витягає по двох вузла, x і y, які характеризуються в черзі найменшими частотами, і заміняє їх у черзі новим вузлом z, що представляє об'єднання згаданих вище елементів. Частота появи z обчислюється в рядку 7 як сума частот x і y. Вузол x є лівим дочірнім вузлом z, а y — його правим дочірнім вузлом. (Цей порядок є довільним; перестановка лівих і правого дочірніх вузлів • приводить до створення іншого коду з тією же вартістю. ) Після n - 1 об'єднань у черзі залишається один вузол — корінь дерева кодів, що вертається в рядку 9.

8. 3 Коди Хаффмена • Алгоритм будує оптимальне дерево префіксних кодів. Для цього в циклі виконується вибірка із черги двох вершин x і y з найменьшими частотами (f[x] і f[y] відповідно), які заміняються на одну вершину z із частотою f[x] + f[y] і дітьми x і y. • Алгоритм працює за O(nlog 2 n) для алфавіту з n символів. Уважаючи що, черга Q реалізована у вигляді двійкової купи, ми можемо виконати ініціалізацію Q за O(n), а кожну операцію над купою за O(log 2 n). • Правильність алгоритму Хаффмена • Доведемо, що для завдання про оптимальний префіксний код виконується принцип жадібного вибору й властивість оптимальності для підзадач. Приведемо лему, що показує, що виконано принцип жадібного вибору.

8. 3 Коди Хаффмена • Лема 8. 1 Нехай в алфавіті C будь-який символ c C має частоту f[c]. Нехай x, y C — два символи з найменшими частотами. Тоді для C є оптимальний префиксный код, у якому послідовності битов, що кодують x і y, мають однакову довжину й розрізняються тільки в останньому біті. • Лема 8. 2 Вартості відповідних один одному дерев T і T′ (при описаній відповідності) відрізняються на величину f[x] + f[y].

8. 3 Коди Хаффмена • Теорема 8. 2 Жадібний алгоритм Хаффмена будує оптимальний префіксний код. • Доказ. Оптимальні кодові дерева можна шукати серед таких, у яких два найбільш рідкі символи (x і y) є братами (по лемі 1). Їм відповідають дерева для алфавіту З′, у якому x і y злиті в z. Якщо вважати, що f[z] = f[x] + f[y], то по лемі 2 нам залишається знайти оптимальне кодове дерево для алфавіту C′, а потім додати до вершини z двох дітей, позначених символами x і y.

8. 4 Теоретичні основи жадібних алгоритмів • Розглянемо теоретичну основу жадібних алгоритмів - теорію матроїдів. За допомогою неї можна досить часто встановити можливість застосовності жадібного алгоритму. Як потім з'ясується, для цього необхідно, щоб досліджувана множина була матроїдом. • Всі розглянуті графи неорієнтовані. Графовий матроїд графа G будемо позначати M(G). Векторний матроїд матриці A будемо позначати M[A]. • Що є матроїд?

8. 4 Теоретичні основи жадібних алгоритмів • Розглянемо наступну матрицю. • Визначимо множину E як можину, що складається з {1, 2, 3, 4, 5, 6, 7} — номерів стовпців матриці, а множину I як множину, що складається з підмножин E, таких, що вектори, обумовлені ними, є лінійно незалежними над полем дійсних чисел R. Задамося питанням — якими властивостями володіє побудована множина I? 1 0 0 0 0 1 1 1 0 0 0 1 1 0

• • • Множина I непорожня. Навіть якщо вихідна множина E була порожньою — E = Ø, те I буде складатися з одного елемента — множини, що містить порожню I = {{Ø}}. Будь-яка підмножина будь-якого елемента множини I також буде елементом цієї множини. Це властивість зрозуміла - якщо деякий набір векторів лінійно незалежний над полем, те лінійно незалежним буде також будь-який його піднабір. Також у множини I є ще одна важлива й досить нетривіальна властивість. Якщо X, Y I, причому |X| = |Y| + 1, тоді існує елемент x X − Y такий, що Y {x} I. На даний момент воно може здатися трохи дивним і неочевидним. Небагато пізніше картина проясниться.
8_ukr.ppt