Тема 8 Спинтроника Спиновые явления в квантовых точках

Тема 8. Спинтроника Спиновые явления в квантовых точках

Спин George Uhlenbeck 1925 г. Samuel Goudsmit Предложили существование у электрона собственного механического момента и связанного с ним магнитного момента. Несколькими годами раньше идею спина пытались озвучить Артур Комптон и Ральф Крониг, однако не встретив сочувствия авторитетов того времени (В. Паули, Х. Крамерс, В. Гейзенберг) идея была отвергнута.

Гипотеза спина объяснила ряд ключевых экспериментальных фактов. 1. Дублетная структура спектральных линий, названная тонкой структурой. 2. Эксперименты Штерна-Герлаха (1922), по – расщепление пучка атомов серебра после прохождения через неоднородное магнитное поле на два пучка. 3. Расщепление спектральных линий в магнитном поле – эффект Зеемана. Эти эксперименты были объяснены только после введения гипотезы спина собственного углового момента и собственного магнитного момента электрона. Классически, электронный магнитный момент мог бы возникнуть при вращении электрона вокруг собственной оси.

• В физике полупроводников до 1990 -х годов спиновые явления рассматривались, в основном, в рамках статистики Ферми – Дирака или для описания энергетической структуры атомо-подобных образований, таких как экситоны большого радиуса или носители заряда, локализованные возле атомов примесей и дефектов. • Это было связно в первую очередь с тем, что полупроводниковые приборы от первого транзистора до самой современной микросхемы построены, как правило, на принципе переноса электрического заряда.

Первые эксперименты в полупроводниках: 1968 (Si) Georges Lampel – Ecole Polytechnique Paris 1970 -e и 1980 -e ФТИ им. Иоффе – Ленинград Обнаружение оптической ориентации в полупроводниках G. Lampel (1968), Парсонс (1970), Б. П. Захарченя с сотр. (1971), теория – М. И. Дьяконов, В. И. Перель (1971). G. Lampel А. Н. Титков Б. П. Захарченя М. И. Дьяконов, М. Е. Левинштейн, В. И. Перель

Спинтроника Область деятельности, направленная на изучение возможности управлением спиновой степенью свободы в твердых телах Цель: изучение взаимодействия спина носителя заряда с окружающей средой, для создания на основе полученного знания электронных приборов. Основные области исследования: спиновый транспорт, оптическая ориентация спина, спиновая релаксация.

Спинтроника Основные проблемы, стоящие перед исследователями: 1. Поиск эффективных способов поляризации спина системы 2. Определение времени, в течение которого система помнит спиновую поляризацию. Управление этим временем, посредством приложения внешних полей. 3. Детектирование системы спинового состояния

Инжекция спин-поляризованных электронов Идея создания неравновесной спиновой поляризации в полупроводнике при пропускании тока через ферромагнитный контакт предложена Ароновым и Пикусом. А. Г. Аронов, Г. Е. Пикус, 1976, ФТП, 10, 1177 Впервые экспериментально спиновая инжекция была реализована Альварадо и Рено. L L = (D s )1/2 S. F. Alvarado and P. Renaud. Phys. Rev. Lett 68 1387 -1390 (1992)

Инжекция спин-поляризованных электронов Albert Fert Peter Grünberg Нобелевская премия по физике 2007 года присуждена за открытие гигантского магнитосопротивления.

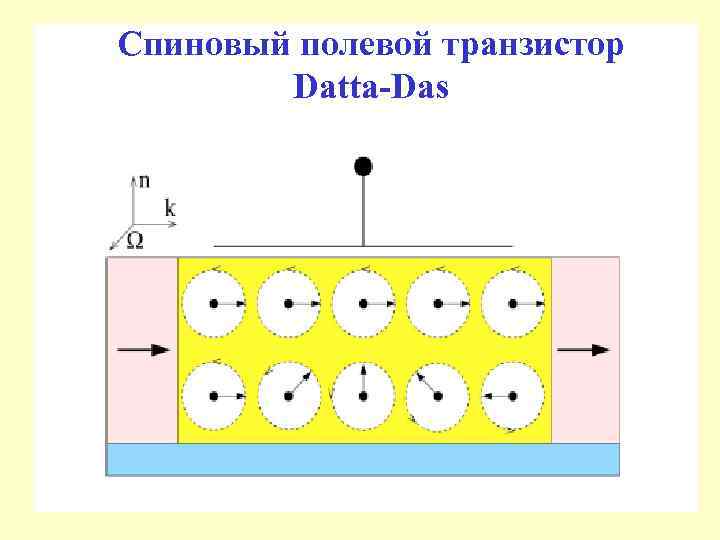Спиновый полевой транзистор Datta-Das

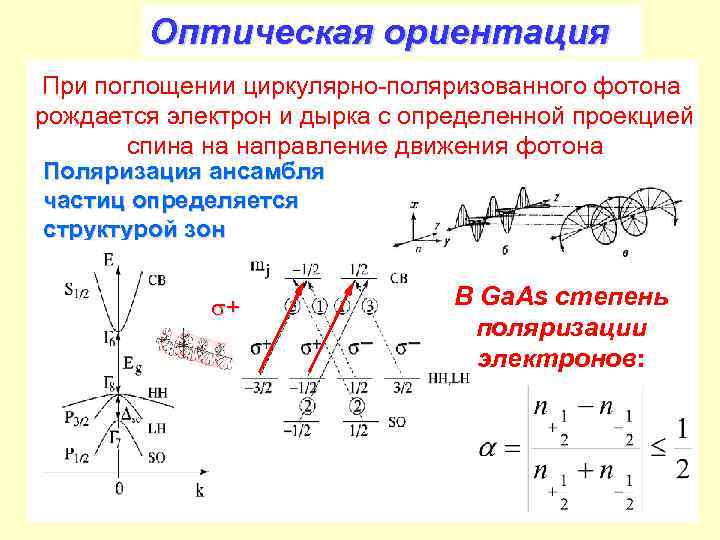Оптическая ориентация При поглощении циркулярно-поляризованного фотона рождается электрон и дырка с определенной проекцией спина на направление движения фотона Поляризация ансамбля частиц определяется структурой зон + В Ga. As степень поляризации электронов:

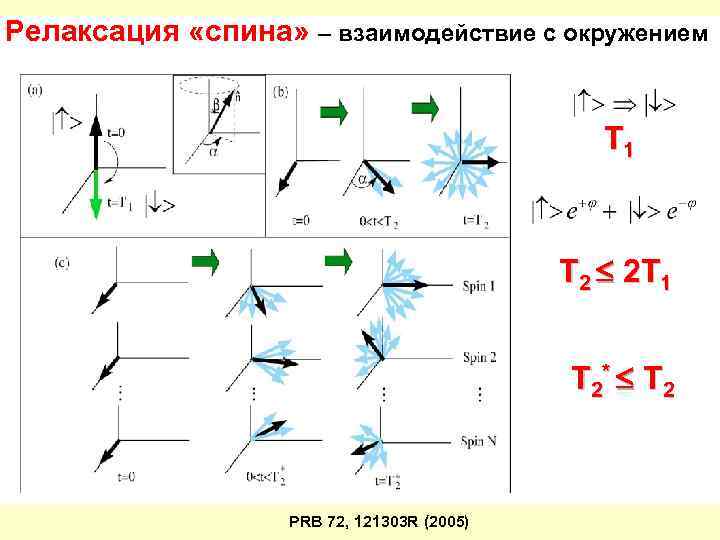Релаксация «спина» – взаимодействие с окружением T 1 T 2 2 T 1 T 2* T 2 PRB 72, 121303 R (2005)

Внешние воздействия на спин могут быть описаны как результат влияния флуктуирующего во времени магнитного поля – реального или эффективного Эффективное магнитное поле может возникать в результате магнитных взаимодействий. (1) Диполь-дипольное взаимодействие магнитных моментов пары электронов. Для электронов расположенных в соседних узлах кристаллической решетки энергия этого взаимодействия порядка 1 К. (2) Спин-орбитальное взаимодействие. Для электрона, движущегося в электрическом поле (стационарном или изменяющимся ) E со скорость v возникает эффективное магнитное поле H=[(v/c)x. E].

(3) Обменное взаимодействие. Кулоновское взаимодействие + принцип Паули. Ответственно за поляризацию спинов электронов в ферромагнетиках. (4) Сверхтонкое взаимодействие со спинами ядер. 100% поляризация спинов ядер в Ga. As может привести к появлению магнитного поля в несколько Тесла!!!. Поляризовать ядерные спины очень просто!!! (5) Отсутствие центра инверсии, например, в некоторых кристаллах A 3 -B 5 приводит к появлению H(K).

Релаксация поляризации спина Основные механизмы спиновой релаксации в п/п Эллиота-Яфета изменение проекции спина при рассеянии на примеси или фононе в эффективном магнитном поле спинорбитального взаимодействия Бира-Аронова-Пикуса изменение проекции спина при рассеянии на дырке в результате обменного взаимодействия Дьяконова - Переля изменение проекции спина в промежутке между двумя последовательными рассеяния Сверхтонкое взаимодействие релаксация спина электрона в магнитном поле, создаваемом спинами ядер.

Релаксация поляризации спина Механизм Эллиота-Яфета A – безразмерная константа Wg – ширина запрещенной зоны h= /( + Wg), – спин-орбитальное расщепление p – время релаксации импульса

Релаксация поляризации спина Механизм Дьяконова - Переля Прецессия спина вокруг магнитного поля, с частотой L величина поля зависит от направления движения электрона Если p L>>1 то s =1/ L Если p L<<1 то за время t, (t/ p) малых поворотов на случайный угол i. i 2 =( p L)2 s = 2 p < i 2> = (t/ p) ( p L)2 = 1

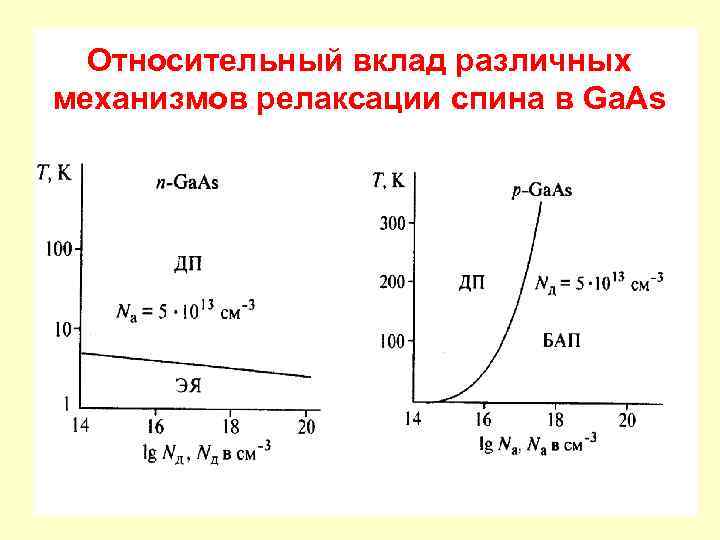Относительный вклад различных механизмов релаксации спина в Ga. As

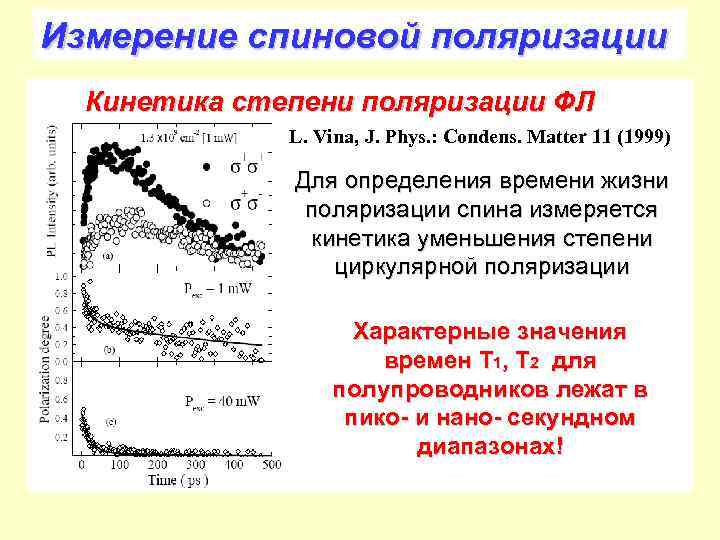Измерение спиновой поляризации Кинетика степени поляризации ФЛ L. Vina, J. Phys. : Condens. Matter 11 (1999) Для определения времени жизни поляризации спина измеряется кинетика уменьшения степени циркулярной поляризации Характерные значения времен T 1, T 2 для полупроводников лежат в пико- и нано- секундном диапазонах!

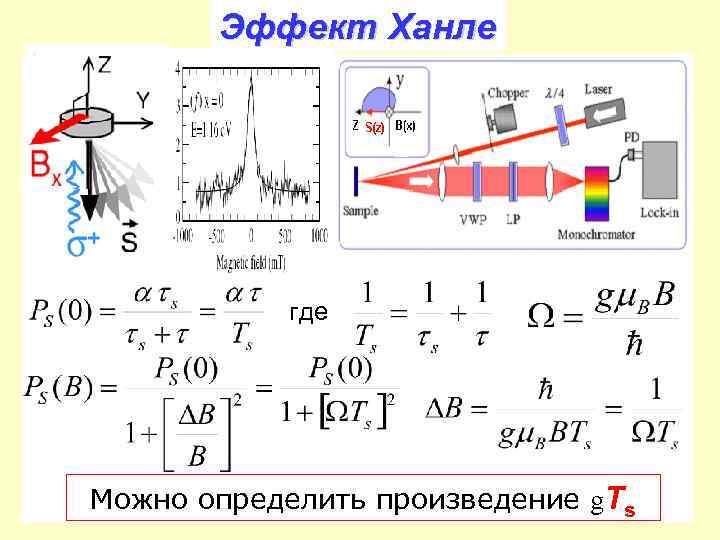Эффект Ханле где Можно определить произведение g. Ts

Перспектива использования спина носителя заряда или экситона, локализованного в квантовой точке, в качестве единицы информации, кубита (qbit), породила «взрывообразный» взрывообразный интерес к изучению спиновой ориентации и спиновой релаксации в структурах с квантовыми точками bit: |+>; |- > два состояния qbit : |+>; |- >; a |+ > + b |- > a 2+b 2=1 два состояния + когерентная суперпозиция состояний

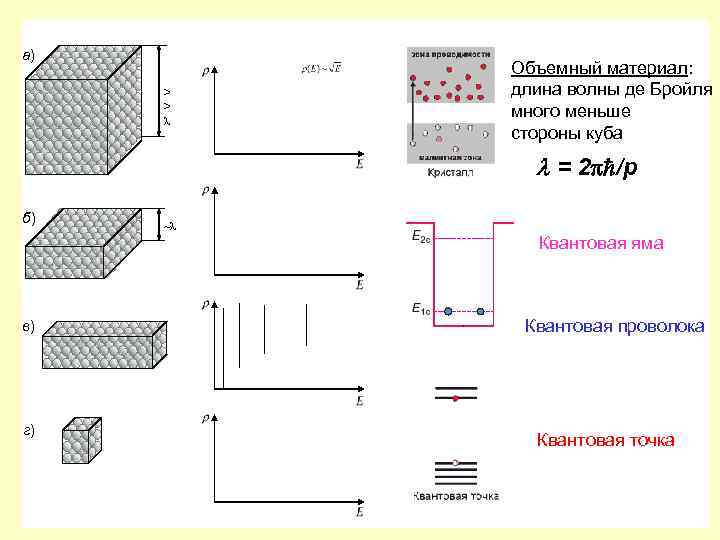а) > > λ Объемный материал: длина волны де Бройля много меньше стороны куба = 2 /p б) ~λ Квантовая яма в) г) Квантовая проволока Квантовая точка

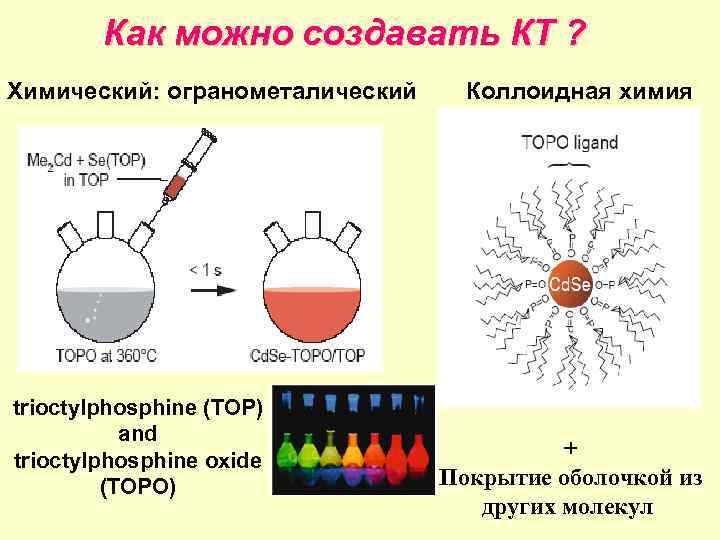Как можно создавать КТ ? Химический: огранометалический trioctylphosphine (TOP) and trioctylphosphine oxide (TOPO) Коллоидная химия + Покрытие оболочкой из других молекул

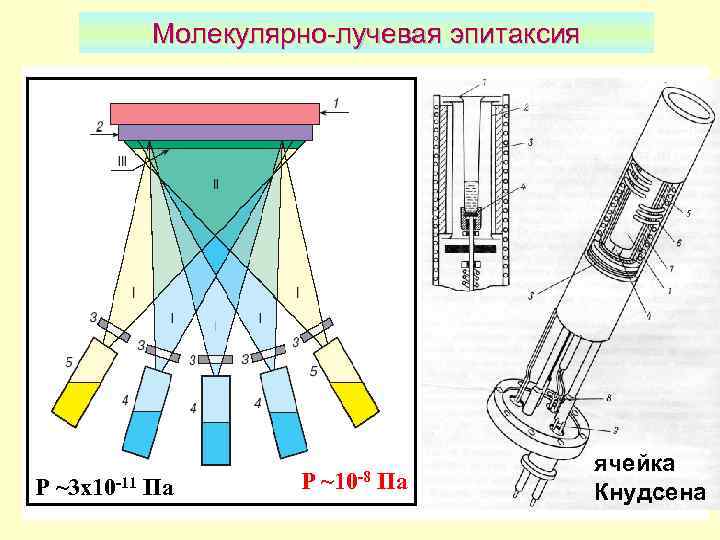Молекулярно-лучевая эпитаксия 1 - держатель с нагревателем 2 - подложка 3 – заслонки 4, 5 – эффузионные ячейки I – поток молекул II – область "полезного" роста III – растущая пленка P ~3 x 10 -11 Па P ~10 -8 Па ячейка Кнудсена

Как можно создавать КТ ? Возможные механизмы роста при гетероэпитаксии • Большая поверхностная энергия подложки – формирование “смачивающего слоя“ Frank van der Merwe • Большая поверхностная осаждаемого материала – подложка не смачивается, островковый рост Volmer-Weber • Большая упругая энергия пленки – образование трехмерных островков Stranski-Krastanow

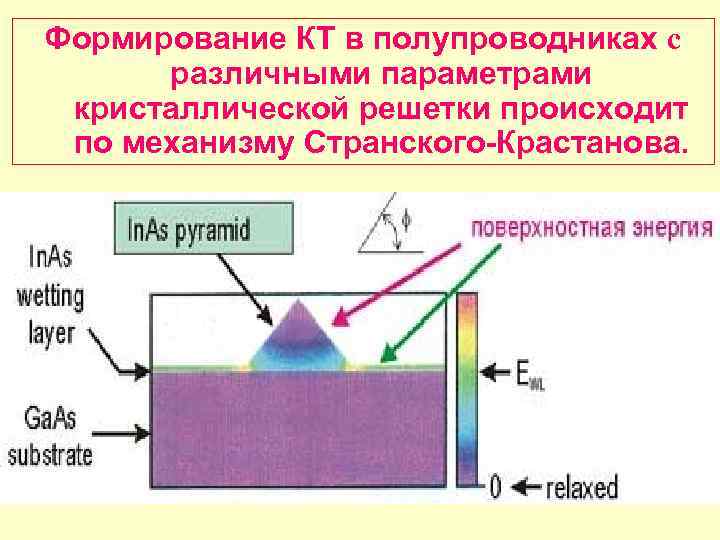Формирование КТ в полупроводниках c различными параметрами кристаллической решетки происходит по механизму Странского-Крастанова.

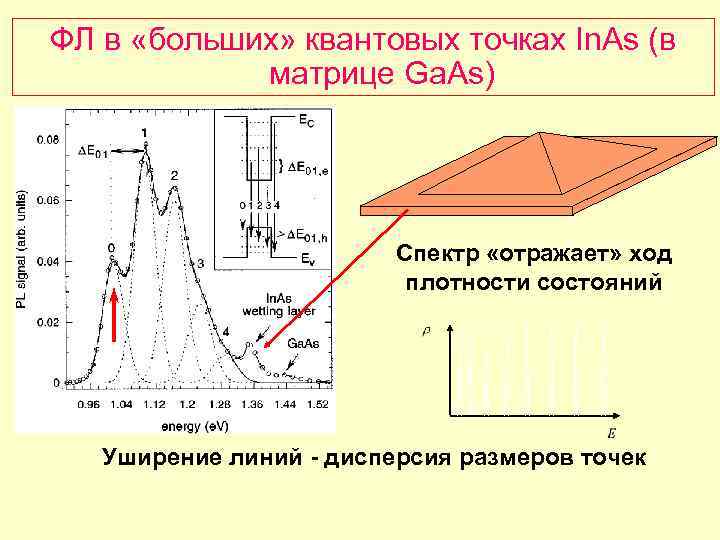ФЛ в «больших» квантовых точках In. As (в матрице Ga. As) Спектр «отражает» ход плотности состояний Уширение линий - дисперсия размеров точек

Чем отличаются КТ от объемных ПП ? Теоретиками было показано, что дискретная структура энергетических уровней КТ приводит к подавлению механизмов, определяющих переворот спина электронов в зоне проводимости, таких как механизмы Эллиота-Яфета и Дьяконова–Переля. основным механизмом становится: релаксации спина сверхтонкое взаимодействие Ожидалось значительное замедление времени спиновой релаксации в КТ

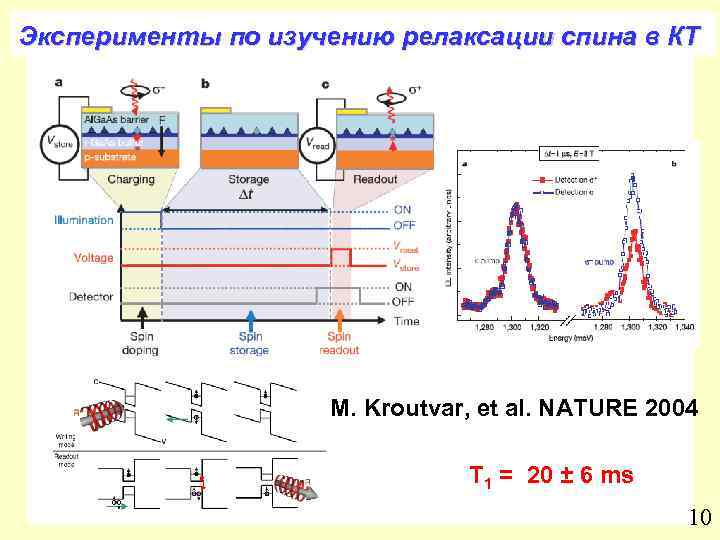Эксперименты по изучению релаксации спина в КТ M. Kroutvar, et al. NATURE 2004 T 1 = 20 ± 6 ms 10

Тонкая структура экситонных уровней Объемный материал H. Fu, Lin-Wang, Alex Zunger Phys. Rev. B 59, 5568 (1999).

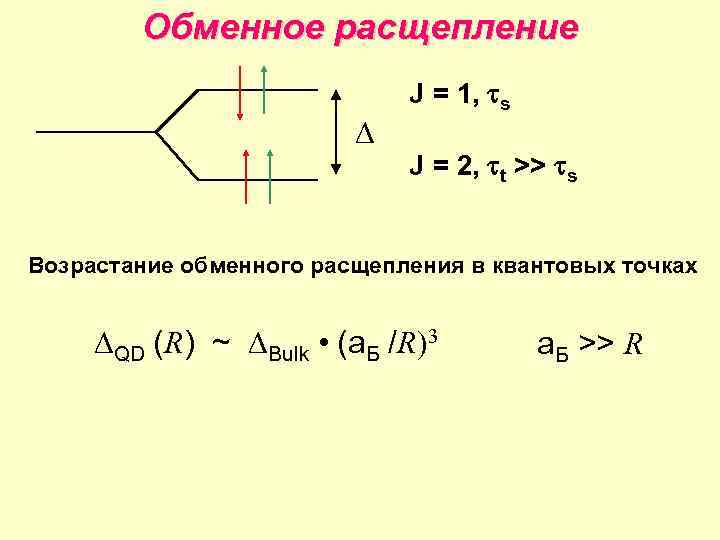Обменное расщепление J = 1, s J = 2, t >> s Возрастание обменного расщепления в квантовых точках QD (R) ~ Bulk • (a. Б /R)3 a. Б >> R

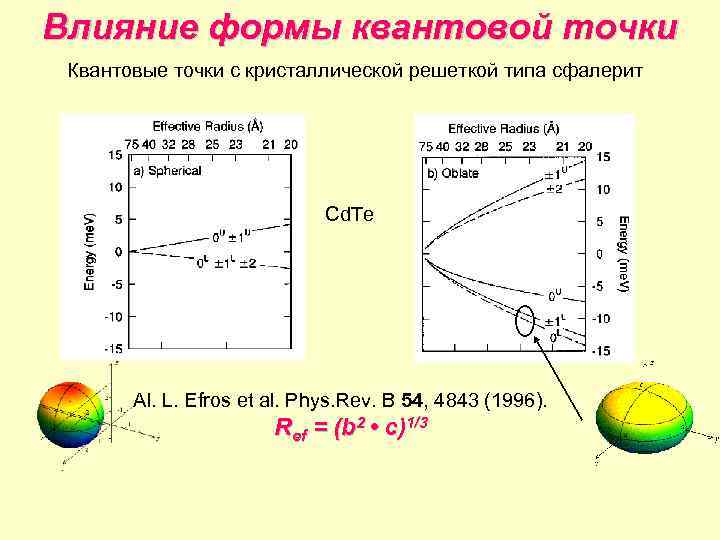Влияние формы квантовой точки Квантовые точки с кристаллической решеткой типа сфалерит Cd. Te Al. L. Efros et al. Phys. Rev. B 54, 4843 (1996). Ref = (b 2 • c)1/3

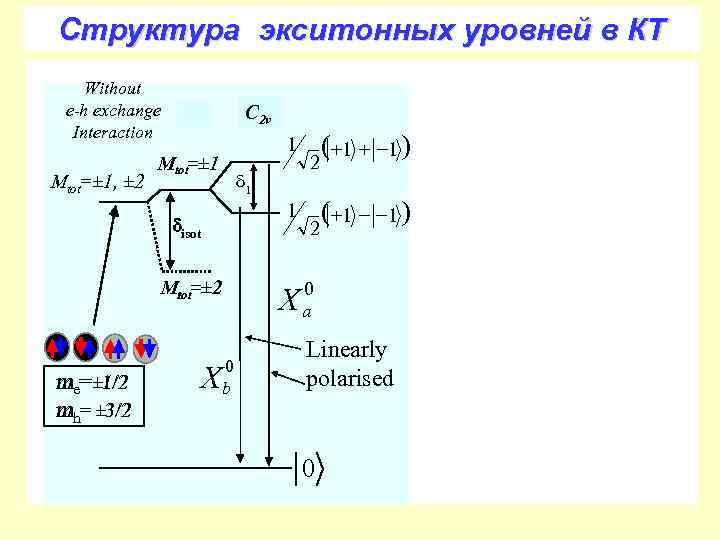Cтруктура экситонных уровней в КТ Without e-h exchange Interaction Mtot=± 1, ± 2 C 2 v

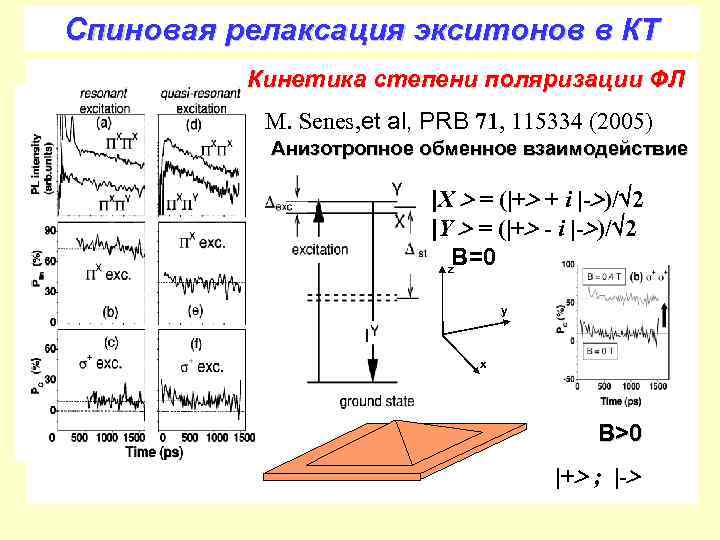Cпиновая релаксация экситонов в КТ Кинетика степени поляризации ФЛ M. Senes, et al, PRВ 71, 115334 (2005) Анизотропное обменное взаимодействие |X = (|+ + i |- )/ 2 |Y = (|+ - i |- )/ 2 B=0 z y x B>0 |+ ; |-

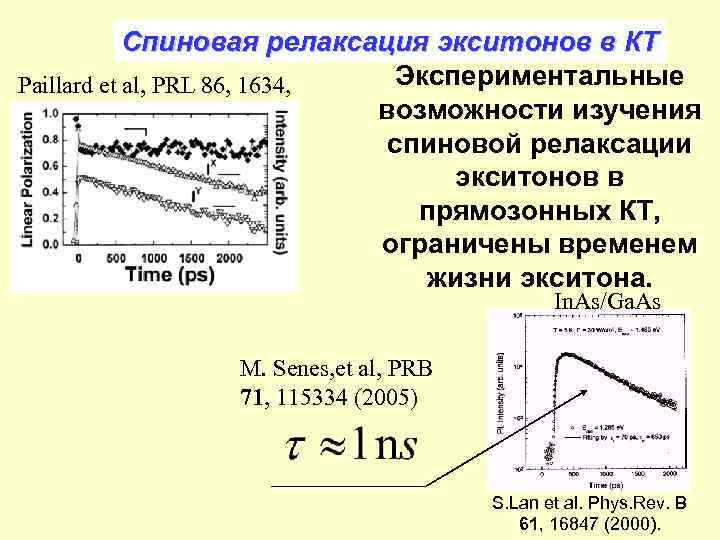Спиновая релаксация экситонов в КТ Экспериментальные Paillard et al, PRL 86, 1634, возможности изучения 2001 спиновой релаксации экситонов в прямозонных КТ, ограничены временем жизни экситона. In. As/Ga. As M. Senes, et al, PRВ 71, 115334 (2005) S. Lan et al. Phys. Rev. B 61, 16847 (2000).

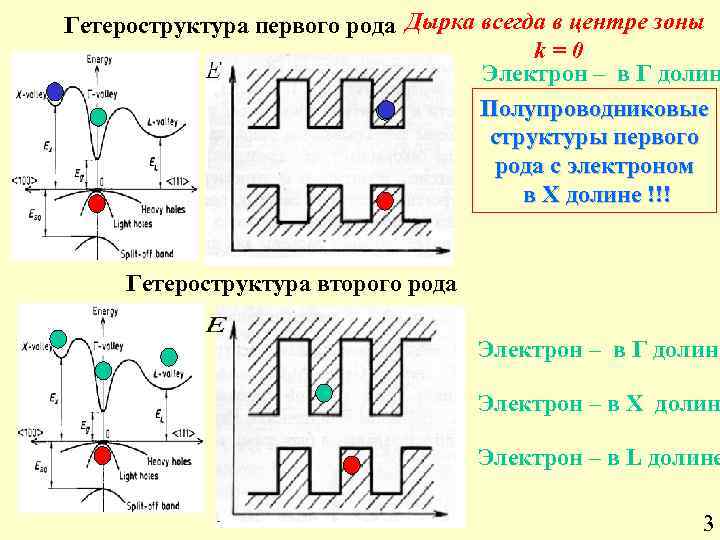Гетероструктура первого рода Дырка всегда в центре зоны k=0 Электрон – в Г долин Полупроводниковые структуры первого рода с электроном в Х долине !!! Гетероструктура второго рода Электрон – в Г долине Электрон – в X долин Электрон – в L долине 3

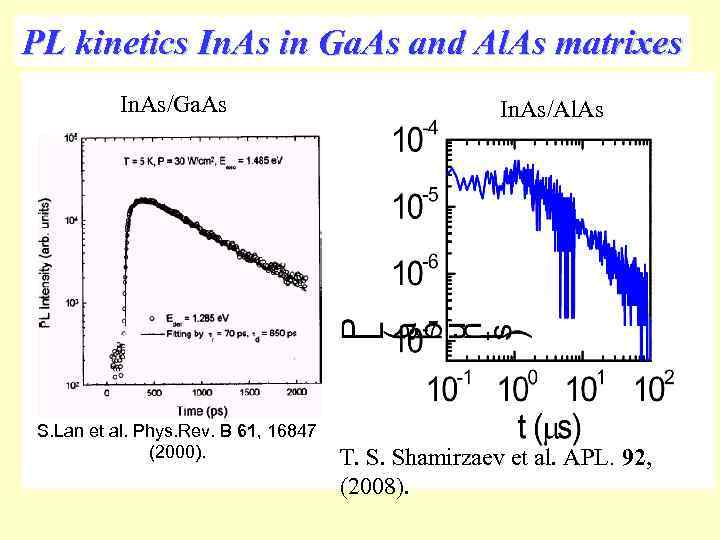PL kinetics In. As in Ga. As and Al. As matrixes In. As/Ga. As S. Lan et al. Phys. Rev. B 61, 16847 (2000). In. As/Al. As T. S. Shamirzaev et al. APL. 92, (2008).

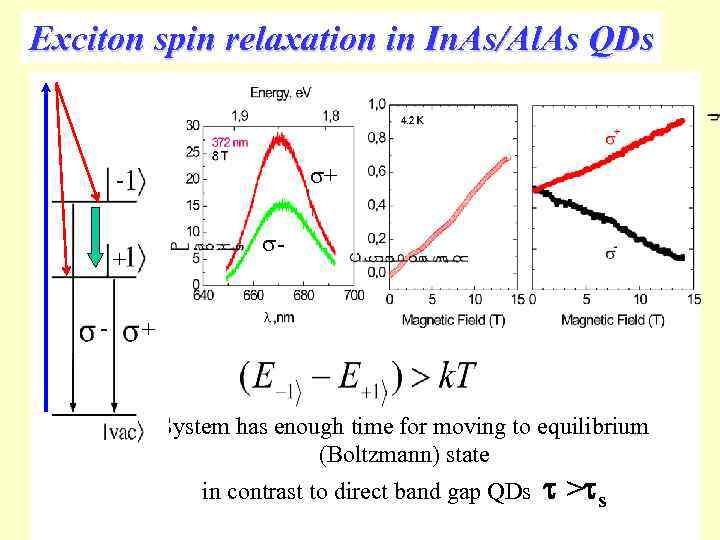Exciton spin relaxation in In. As/Al. As QDs + - + System has enough time for moving to equilibrium (Boltzmann) state in contrast to direct band gap QDs > s

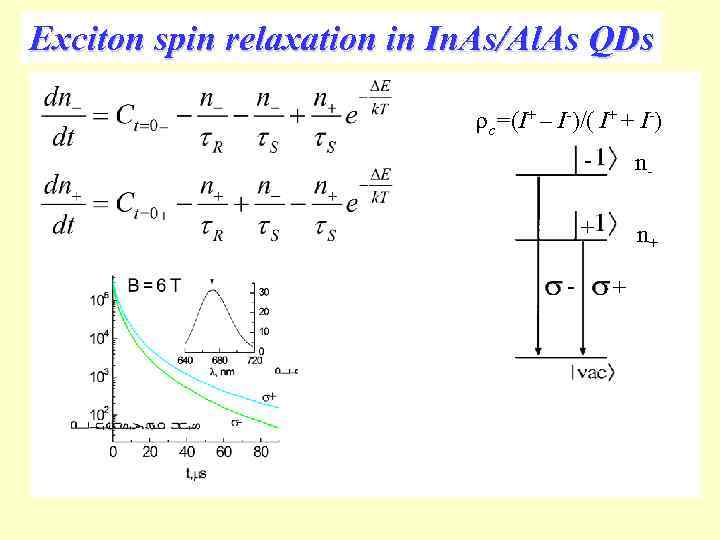Exciton spin relaxation in In. As/Al. As QDs c=(I+ – I-)/( I+ + I-) + - nn+ +

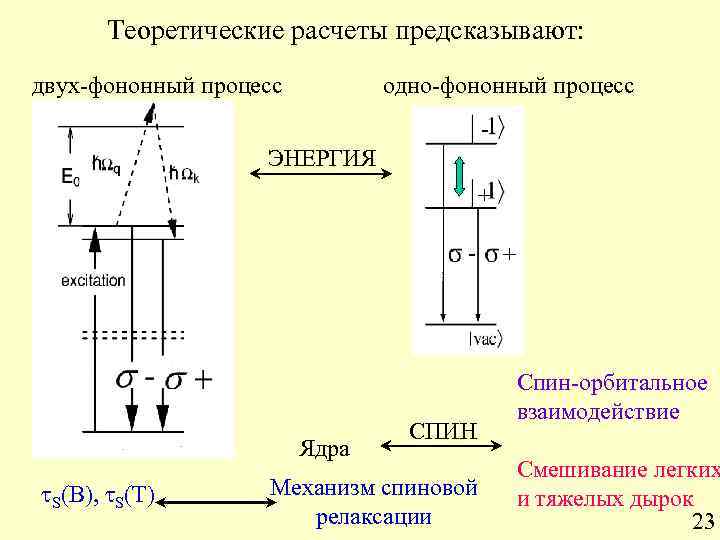Теоретические расчеты предсказывают: двух-фононный процесс одно-фононный процесс - ЭНЕРГИЯ + - Ядра S(B), S(T) СПИН Механизм спиновой релаксации + Спин-орбитальное взаимодействие Смешивание легких и тяжелых дырок 23

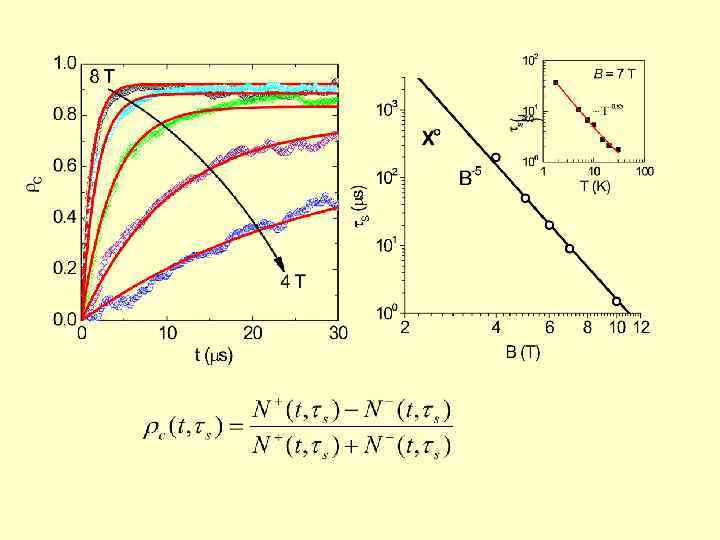
The fashion of quantum computer building will gradually die away, the sooner, the better. Research in atomic and spin physics is interesting and useful on its own and need not be justified by irresponsible projects and promises. “QUANTUM COMPUTING: A VIEW FROM THE ENEMY CAMP” M. I. Dyakonov