Тема 8 Основы квантовой механики Корпускулярно-волновой дуализм

Тема 8. Основы квантовой механики. • Корпускулярно-волновой дуализм света • Волны де Бройля • Соотношение неопределенностей • Волновая функция. Уравнение Шредингера • Парадоксы квантовой механики

Корпускулярно-волновые свойства света • Согласно корпускулярной теории, свет представляет собой поток частиц (корпускул), испускаемых светящимися телами, движение световых корпускул подчиняется законам механики. (Ньютон) • Волновая теория рассматривает свет как волновой процесс, подобный механическим волнам. (Гюйгенс)

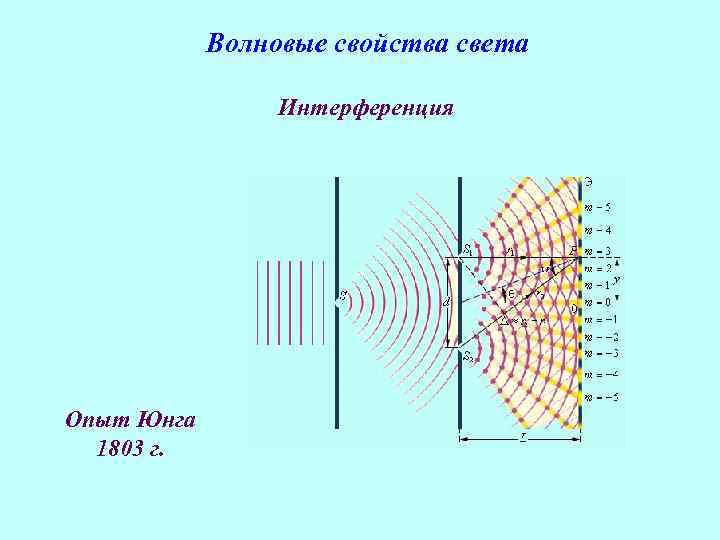Волновые свойства света Интерференция Опыт Юнга 1803 г.

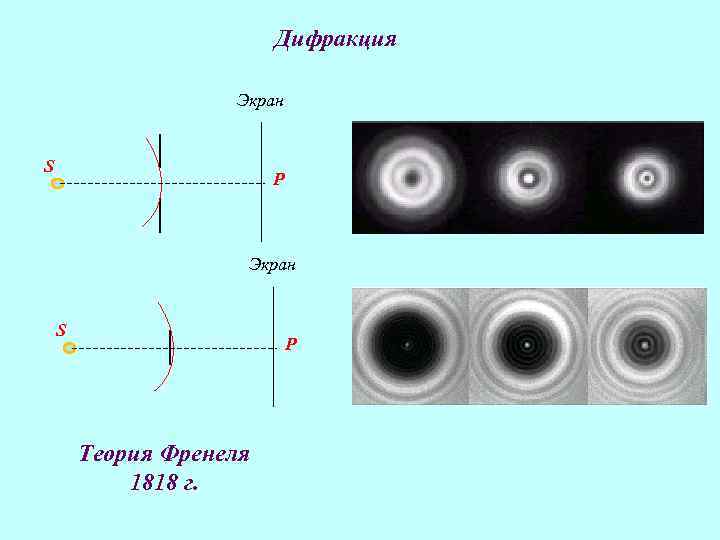Дифракция Экран S P Теория Френеля 1818 г.

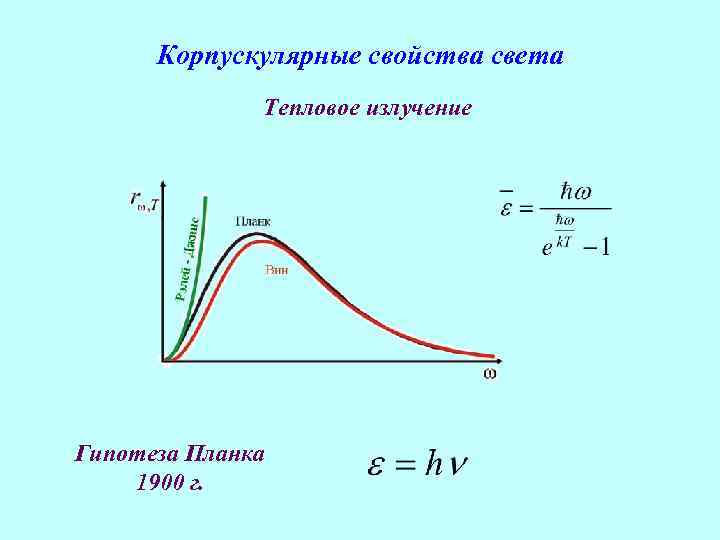Корпускулярные свойства света Тепловое излучение Гипотеза Планка 1900 г.

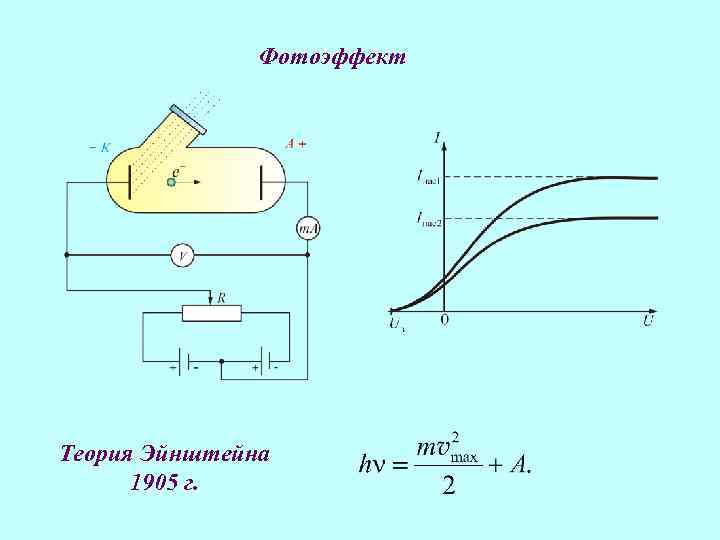Фотоэффект Теория Эйнштейна 1905 г.

Физическая величина действие (S): В классической механике : ( T и U – потенциальная и кинетическая энергии) Размерность действия: (энергия)х(время) (импульс)х(координата) (момент импульса) Размерность действия совпадает с размерностью постоянной Планка h

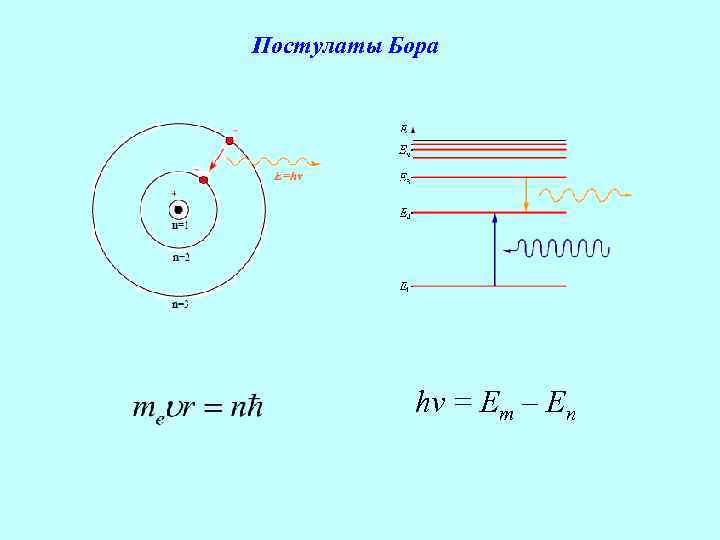Постулаты Бора hv = Em – En

Волны де Бройля В 1924 г. Луи де Бройль предположил, что двойственность свойств волна – частица является универсальной и присуща не только свету, но и любым частицам, например, электронам, протонам, нейтронам, атомам, молекулам и т. д. Согласно гипотезе де Бройля, любой движущейся частице должен соответствовать некоторый волновой процесс, и корпускулярные характеристики частицы (энергия, импульс) должны быть связаны с волновыми свойствами (частота, длина волны) теми же соотношениями, что и для фотонов: Louis de Broglie 1892 -1987

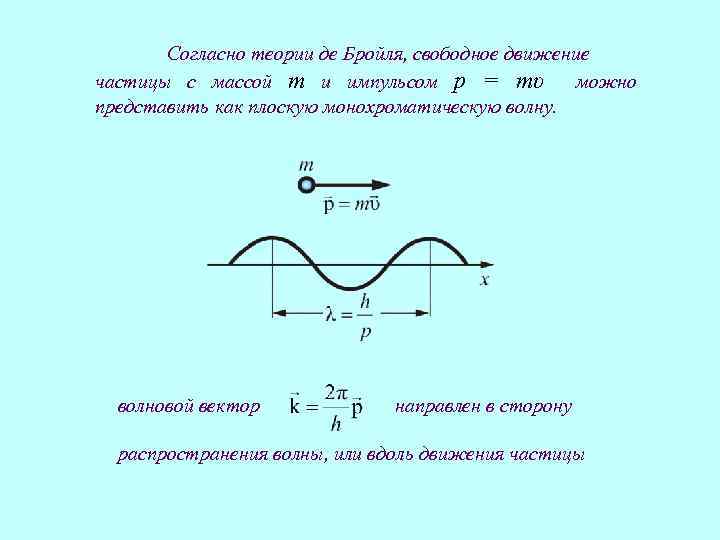Согласно теории де Бройля, свободное движение частицы с массой m и импульсом p = mυ можно представить как плоскую монохроматическую волну. волновой вектор направлен в сторону распространения волны, или вдоль движения частицы

Свет (фотоны) Частицы (электроны, протоны и пр. ) Волновые свойства Корпускулярные свойства длина волны λ (k=2π/ λ) импульс p=mυ частота ν (ω=2πν) энергия E=p 2/2 m (нерелятивистский случай) λ·ν=с Корпускулярные свойства Волновые свойства энергия E=hν=ћω длина волны λ=h/p импульс p=h/λ=hν/c частота ν=E/h (ω=E/ћ)

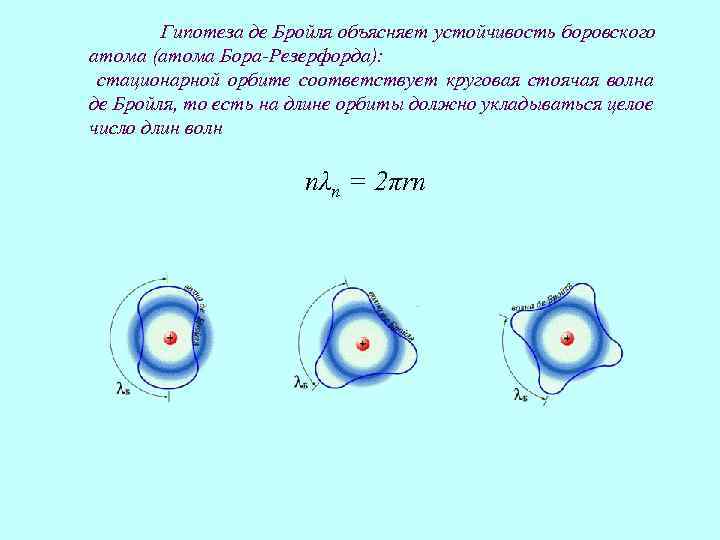Гипотеза де Бройля объясняет устойчивость боровского атома (атома Бора-Резерфорда): стационарной орбите соответствует круговая стоячая волна де Бройля, то есть на длине орбиты должно укладываться целое число длин волн nλn = 2πrn

Пример: Рассчитать радиус орбиты электрона в атоме водорода, на которой укладывается одна длина волны де Бройля. согласно 2 -му закону Ньютона для атома водорода: длина волны де Бройля: если на орбите укладывается одна длина волны, то: подставляя, получаем:

Корпускулярно-волновой дуализм - универсальное свойство природы, заключающееся в том, что всем микрообъектам присущи одновременно и корпускулярные и волновые характеристики.

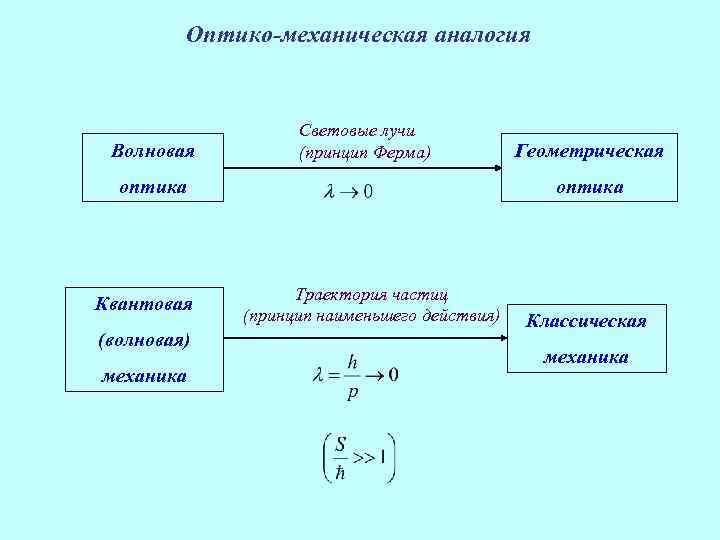Оптико-механическая аналогия Волновая Световые лучи (принцип Ферма) оптика Квантовая (волновая) механика Геометрическая оптика Траектория частиц (принцип наименьшего действия) Классическая механика

Пример 1 Определить длину волны де Бройля пылинки массой 1 мг, движущейся со скоростью 1 мм/с. Длина волны де Бройля: Вывод: Даже для очень маленького макроскопического объекта длина волны де Бройля слишком мала, чтобы можно было наблюдать какоелибо отклонение от законов классической физики.

Пример 2 Определить длину волны де Бройля для электрона, ускоренного разностью потенциалов 100 В. Длина волны де Бройля: поскольку : и окончательно получаем: Вывод: Длина волны электрона, ускоренного разностью потенциалов порядка 100 вольт, соизмерима с межатомными расстояниями, т. е. возможна дифракция электрона на кристаллической решетке

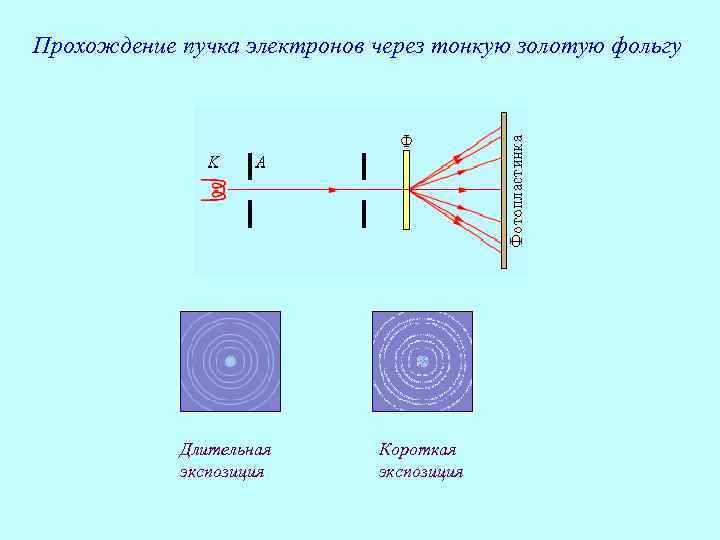Прохождение пучка электронов через тонкую золотую фольгу Длительная экспозиция Короткая экспозиция

Принцип неопределённости Гейзенберга (соотношение неопределённостей) - фундаментальное неравенство, устанавливающее предел точности одновременного определения пары характеризующих квантовую систему физических наблюдаемых, например: Werner Karl Heisenberg 1901 -1976

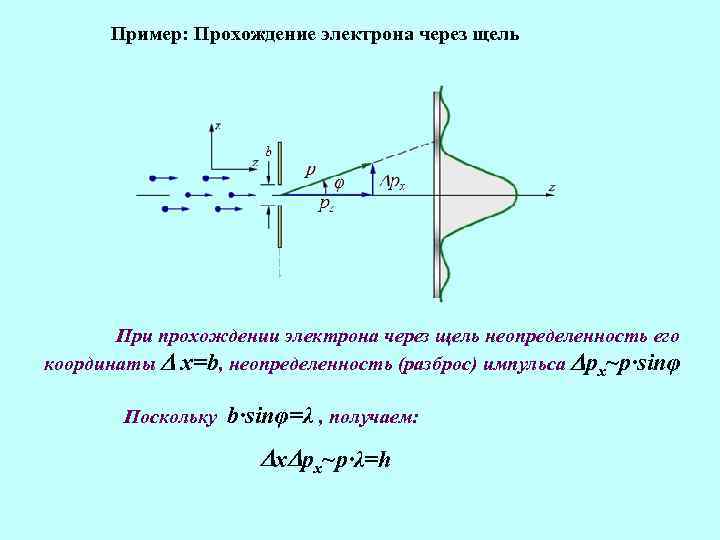Пример: Прохождение электрона через щель При прохождении электрона через щель неопределенность его координаты x=b, неопределенность (разброс) импульса px~p∙sinφ Поскольку b∙sinφ=λ , получаем: x px~p∙λ=h

Принцип дополнительности Сформулирован в 1927 году Нильсом Бором При точном измерении одной из дополнительных величии (например, координаты частицы) с помощью соответствующего прибора, другая величина (импульс) в результате взаимодействия частицы с прибором претерпевает полностью неконтролируемое изменение. Роль измерительного прибора: ни импульс, ни координата (ни другие «классические» свойства) микрочастицы не существуют сами по себе, а проявляются лишь во взаимодействии с классическим прибором.

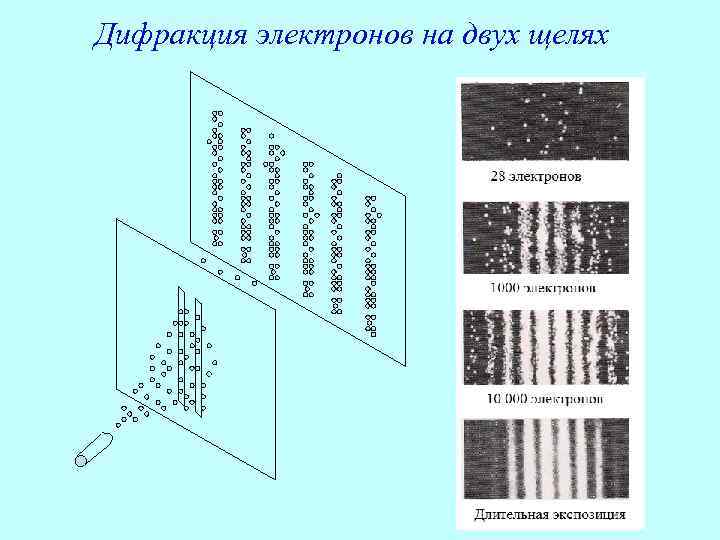Дифракция электронов на двух щелях

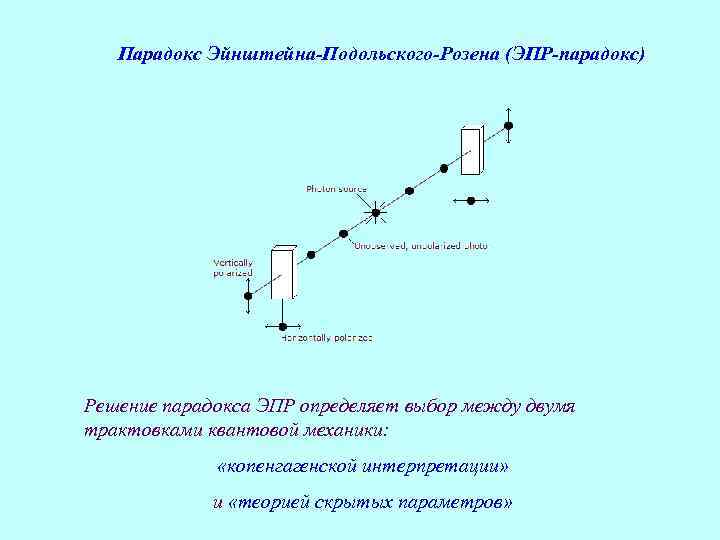Парадокс Эйнштейна-Подольского-Розена (ЭПР-парадокс) Решение парадокса ЭПР определяет выбор между двумя трактовками квантовой механики: «копенгагенской интерпретации» и «теорией скрытых параметров»

Волновая функция В классической физике состояние частицы можно описать задав ее координаты и скорость (импульс). В квантовой механике это сделать невозможно из-за соотношения неопределенности Состояние частицы в квантовой механике задается волновой функцией (пси-функцией): Уравнение Шредингера (для стационарных состояний): Эрвин Шредингер 1887 -1961

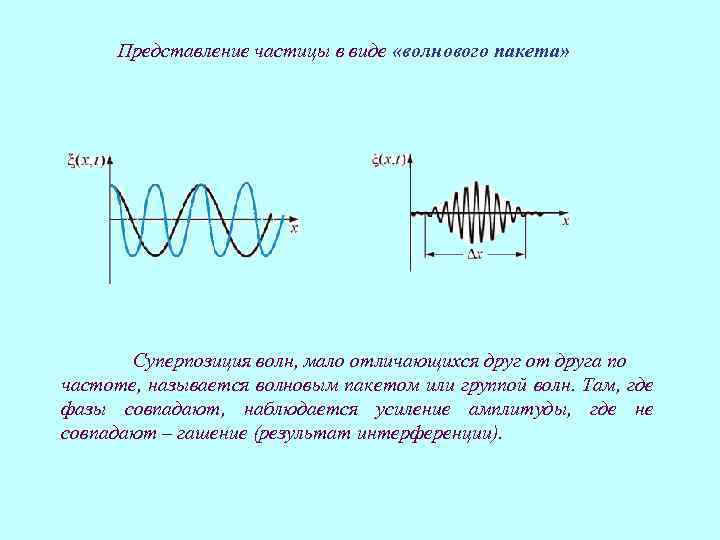Представление частицы в виде «волнового пакета» Суперпозиция волн, мало отличающихся друг от друга по частоте, называется волновым пакетом или группой волн. Там, где фазы совпадают, наблюдается усиление амплитуды, где не совпадают – гашение (результат интерференции).

Расчеты показывают, волновой пакет должен «размываться» даже в вакууме, т. е. частица-волновой пакет будет неустойчива. Представление о частице как о волновом пакете оказалось несостоятельным. Проблема двойственности свойств частиц (корпускулярно-волновой дуализм) принципиально не может быть решена в рамках классического подхода.

Физический смысл имеет не сама волновая функция, а квадрат ее модуля: Квадрат модуля волновой функции определяет вероятность нахождения частицы в объеме d. V: Макс Борн 1882 -1970 Пси-функция недоступна наблюдению!

Принцип суперпозиции пси-функций, один из основных принципов квантовой механики: Если для некоторой системы возможны состояния Ψ 1 и Ψ 2, то для нее также существует состояние: Ψ=с1Ψ 1+с2Ψ 2

Прохождение электрона через две щели Э Вероятность попадания электрона в т. М через щель a: М Вероятность попадания в т. М через щель b: φa и φb - амплитуды вероятности В классической физике вероятность попадания электрона в т. М : P=Pa+Pb

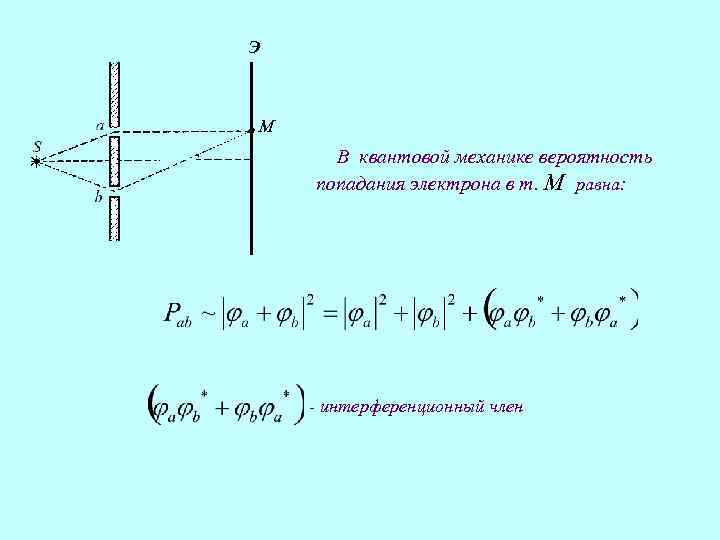Э М В квантовой механике вероятность попадания электрона в т. М равна: - интерференционный член

Парадоксы квантовой механики. Кот Шредингера. В закрытый ящик помещён кот. В ящике есть механизм, содержащий радиоактивное ядро и ёмкость с ядовитым газом. Параметры эксперимента подобраны так, что вероятность того, что ядро распадётся за 1 час, составляет 1/2. Если ядро распадается, оно приводит в действие механизм, который открывает ёмкость с ядовитым газом, и кот умирает.

Пример Определить боровский радиус (радиус первой орбиты атома водорода) исходя из соотношения неопределенностей. 1. Электрон не может упасть на ядро, поскольку тогда его координата точно определена, следовательно импульс будет стремиться к бесконечности 2. Минимальной энергии электрона, движущемуся в кулоновском поле ядра будет соответствовать радиус r= r и импульс p= p. Тогда, согласно принципу неопределенности: p=ћ/r полная энергия электрона: минимум энергии: отсюда: - совпадает с боровским радиусом