Тема 8 Методы формализованного представления систем Методы

Тема 8 Методы формализованного представления систем

Методы формализованного представления систем 1. 2. 3. 4. 5. 6. Аналитические. Статистические. Теоретико множественные. Логические. Лингвистические. Графические

Аналитические методы Методы, которые ряд свойств многомерной, многосвязной системы отображают в n мерном пространстве в виде одной единственной точки, совершающей какие либо перемещения в пространстве (или обладающую каким то поведением). Основу понятийного аппарата этих представлений составляют понятия классической математики (величина, формула, функция, уравнение, система уравнений, логарифм, дифференциал, интеграл и т. д. ).

Аналитические методы На базе аналитических представлений возникли и развиваются математические теории различной сложности: аппарата классического математического анализа (методов исследования функций, их вида, способов представления, поиска экстремумов функций и т. п. ) математическое программирование (линейное, нелинейное, динамическое и т. п. ), теория игр (матричные игры с чистыми стратегиями, дифференциальные игры и т. п. ).

Аналитические методы Прикладные направления использования аналитических методов: решении задач движения и устойчивости, оптимального размещения, распределения работ и ресурсов, выбора наилучшего пути, выбора оптимальной стратегии поведения, в том числе в конфликтных ситуациях и т. п.

Аналитические методы (недостатки) Аналитические методы требуют установления всех детерминированных связей между учитываемыми компонентами и целями системы в виде аналитических зависимостей. Для сложных многокомпонентных, многокритериальных систем получить требуемые аналитические зависимости крайне трудно. Даже если это и удается, то бывает практически невозможно доказать правомерность применения таких выражений, т. е. адекватность модели рассматриваемой задаче.

Статистические методы Статистическим называют отображение системы с помощью случайных (стохастических) событий, процессов, которые описываются вероятностными характеристиками и статистическими закономерностями. Статистические отображения системы можно представить как бы в виде «размытой» точки (размытой области) в n мерном пространстве, при этом границы области заданы с некоторой вероятностью р.

Статистические методы На базе статистических представлений развивается ряд математических теорий: математическая статистика; теория статистических испытаний, основой которой является метод Монте Карло, а развитием теория статистического имитационного моделирования; теория выдвижения и проверки статистических гипотез, базирующаяся на общей теории статистических решающих функций А. Вальда и др.

Статистические методы На базе статистических представлений возникли и развиваются прикладные направления: статистическая радиотехника, статистическая теория распознавания образов, экономическая статистика, теория массового обслуживания и др. Статистические и теоретико множественные методы инициировали возникновение теории нечетких множеств, которая явилась началом развития нового направления нечетких формализаций и т. д

Статистические методы (недостатки) Не всегда: могут быть получены статистические закономерности, может быть определена репрезентативная выборка, может быть доказана правомерность применения статистических закономерностей.

Теоретико-множественные методы Теоретико множественные представления базируются на понятиях множество, элементы множества, отношения на множествах, континуум. Множества могут задаваться следующими способами: 1) перечислением; 2) путем указания некоторого характеристического свойства. В основе теоретико множественных преобразований лежит переход от одного способа задания множества к другому.

Теоретико-множественные методы Множественные представления допускают введение любых произвольных отношений. При конкретизации отношений и правил их использования можно получить одну из алгебр логики, один из формальных языков математической лингвистики, создать язык моделирования сложной системы. Между теоретико множественными описаниями разных систем или их частей можно устанавливать соответствия: гомоморфизма, изоморфизма, авто морфизма, отношения рефлексивности, симметричности, транзитивности, заимствованные теорией множеств из других разделов математики.

Теоретико-множественные методы Благодаря возможности введения любых отношений теоретико множественные представления используются как обобщающий язык при сопоставлении различных направлений математики и других дисциплин. В частности, теоретико множественные представления были использованы для: уточнения ряда математических направлений (теория чисел); становления комбинаторики, топологии; разработки теории нечетких множеств; создания первых информационно поисковых языков, языков автоматизации моделирования.

Теоретико-множественные методы (недостатки) Свобода введения произвольных отношений приводит к тому, что в формализованном с их помощью описании проблемной ситуации довольно быстро могут обнаружиться неразрешимые противоречия, что не позволяет оперировать с получаемыми теоретико множественными моделями таким же образом, как с классическими математическими (аналитическими, статистическими) соотношениями, и не гарантирует достоверность получаемых результатов.

Логические методы Логические представления переводят реальную систему и отношения в ней на язык одной из алгебр логики (двузначной, многозначной. Наибольшее распространение получила бинарная алгебра логики Буля (булева алгебра). Базовыми понятиями алгебры логики являются: высказывание, предикат, логические функции (операции), кванторы, логический базис, логические законы или теоремы (законы алгебры логики), применяя которые можно преобразовать систему из одного описания в другие с целью ее совершенствования.

Логические методы На базе математической логики созданы и развиваются: теории логического анализа и логического cинтеза; теория автоматов; некоторые разделы теории формальных языков.

Логические методы Логические представления широко применяются при разработке: u разного рода автоматов, u автоматических систем контроля, u средств решения задач распознавания образов.

Логические методы (недостатки) С помощью логических алгоритмов можно описывать не любые отношения, а только те, которые предусмотрены законами алгебры логики и удовлетворяют требованиям логического базиса. Двузначная логика не всегда позволяет адекватно отобразить реальную проблемную ситуацию. Поэтому стали предприниматься попытки создания многозначных логик, вплоть до непрерывной. Однако попытки создания многозначных логик на практике пока не находят широкого применения из за сложности обоснования логического базиса и доказательства формальных теорем и законов.

Лингвистические методы Основными понятиями, на которых базируются лингвистические представления, являются: тезаурус, грамматика, семантика, прагматика. Термин тезаурус (от греч. thesauros – сокровищница, запас) множество смысловыражающих элементов языка с заданными смысловыми отношениями. Под грамматикой понимаются правила, с помощью которых формируются смысловыражающие элементы языка. Под семантикой понимается содержание, значение, смысл формируемых или распознаваемых конструкций языка. Под прагматикой полезность для достижения данной цели, решения данной задачи.

Лингвистические методы Для системных приложений интересно сочетание математической лингвистики и семиотики, которая возникла как наука о знаках, знаковых системах.

Лингвистические методы Лингвистические и семиотические представления возникли и развиваются в связи с потребностями анализа текстов на разных языках. Однако во второй половине XX в. эти представления стали широко применяться для отображения и анализа процессов в сложных системах в тех случаях, когда не удается применить сразу аналитические, статистические представления или методы формальной логики.

Лингвистические методы (недостатки) При применении правил произвольной грамматики или семиотики трудно гарантировать достоверность получаемых результатов, возникают проблемы алгоритмической разрешимости. При этом разработчик языка моделирования не всегда может формально объяснить его возможности, происходит как бы «выращивание» языка, у которого появляются новые свойства, повышающие его смысловыражающие возможности.

Графические методы К графическим представлениям относят любые графики (диаграммы, гистограммы и т. п. ) и возникшие на основе графических отображений теории: теория графов, теория сетевого планирования и управления, т. е. все, что позволяет наглядно представить процессы, происходящие в системах, и облегчить таким образом их анализ для человека.

Графические методы Графические представления являются удобным средством исследования структур и процессов в сложных системах, средством организации взаимодействия человека и технических устройств (в том числе ЭВМ).

Графические методы (НЕДОСТАТКИ) Теория СПУ первоначально была ориентирована на анализ только одного класса графов однонаправленных (не имеющих обратных связей, т. е. циклов). Доля «ручного» труда ЛПР при разработке сетевого графика составляет, по оценкам специалистов, до 95% общих затрат времени на анализ ситуаций и процессов с использованием СПУ.

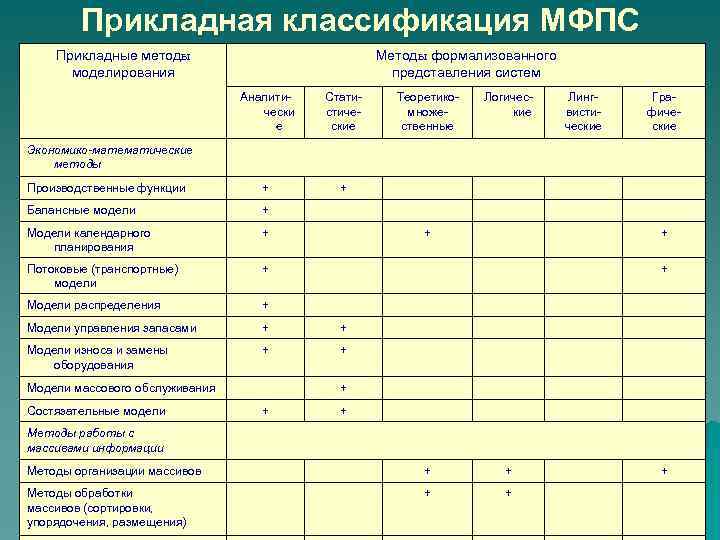Прикладная классификация МФПС Прикладные методы моделирования Методы формализованного представления систем Аналитически е Статистические Производственные функции + + Балансные модели + Модели календарного планирования + Потоковые (транспортные) модели + Модели распределения + Модели управления запасами + + Модели износа и замены оборудования + Теоретикомножественные Логические Лингвистические Графические + Экономико-математические методы Модели массового обслуживания Состязательные модели + + + Методы работы с массивами информации Методы организации массивов + + Методы обработки массивов (сортировки, упорядочения, размещения) + + +