Тема 7 Статистическое изучение вариации Вопросы темы

Тема 7 Статистическое изучение вариации

Вопросы темы: 7. 1. Показатели вариации количественных признаков. 7. 2. Показатели вариации альтернативных признаков. 7. 3. Правило сложения дисперсий и его использование в статистическом анализе. 7. 4. Показатели структуры и их использование в социально-экономических исследованиях.

7. 1 Показатели вариации количественных признаков Вариация характеризуется различием значений признака у разных единиц совокупности в один и тот же период или момент времени.

Показатели вариации ФУНКЦИИ • дают обобщенную оценку меры вариации значений признака в совокупности; • позволяют сделать вывод о типичности (не типичности) средней величины и однородности (неоднородности) совокупности.

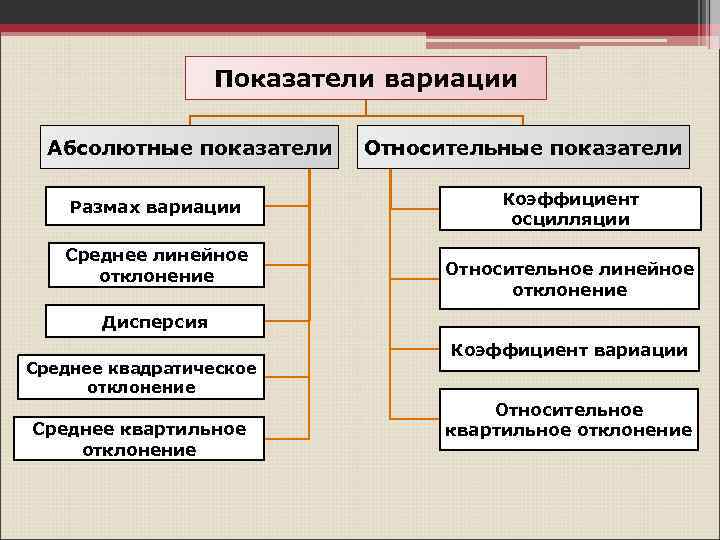Показатели вариации Абсолютные показатели Размах вариации Среднее линейное отклонение Относительные показатели Коэффициент осцилляции Относительное линейное отклонение Дисперсия Среднее квадратическое отклонение Среднее квартильное отклонение Коэффициент вариации Относительное квартильное отклонение

Абсолютные показатели вариации Размах вариации (R) • представляет собой разность между наибольшим и наименьшим значением анализируемого признака:

Абсолютные показатели вариации Среднее линейное отклонение • представляет собой среднюю арифметическую из абсолютных отклонений индивидуальных значений признака от его средней величины: *Cреднее линейное отклонение сохраняет единицу измерения анализируемого признака.

Абсолютные показатели вариации Дисперсия (σ2) • представляет собой средний квадрат отклонений индивидуальных значений признака от его средней величины и рассчитывается по формулам:

С учетом содержания исходных данных, дисперсия может быть рассчитана и по другой формуле: Получается эта формула путем следующего преобразования:

Математические свойства дисперсии • Дисперсия постоянной величины равна нулю: • Если каждое из индивидуальных значений признака уменьшить или увеличить на одно и то же число А, то значение дисперсии не изменится: • Если каждое из индивидуальных значении признака уменьшить в одно то же число раз (k), то дисперсия уменьшится в k 2 раз: • Средний квадрат отклонений индивидуальных значений признака от любой величины А, будет всегда больше среднего квадрата отклонений от средней арифметической, если

Абсолютные показатели вариации Среднее квадратическое отклонение (σ) • показывает, на сколько в среднем отклоняются индивидуальные значения признака от его средней величины:

• Среднее квадратическое отклонение в зарубежной литературе этот показатель называют нормированным или чаще стандартным отклонением. • По свойству мажорантности средних среднее квадратическое отклонение всегда больше среднего линейного отклонения. • Если распределение признака близко к нормальному или симметричному распределению, то между σ и соблюдаются следующие соотношения: Следует отметить, что дисперсия, в отличие от R, d, σ, не сохраняет единицу измерения признака, т. к. квадраты единиц измерения не имеют смысла.

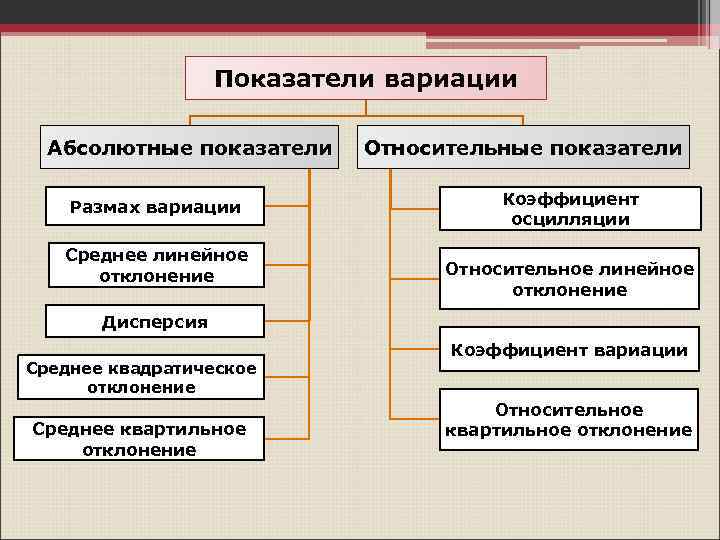Показатели вариации Абсолютные показатели Размах вариации Среднее линейное отклонение Относительные показатели Коэффициент осцилляции Относительное линейное отклонение Дисперсия Среднее квадратическое отклонение Среднее квартильное отклонение Коэффициент вариации Относительное квартильное отклонение

Относительные показатели вариации • используют для целей сравнения изменчивости различных признаков в одной и той же совокупности, а также при сравнении вариации одного и того же признака в нескольких совокупностях (если средний уровень признака различен); • принцип расчета относительных показателей вариации (ОПВ) отражает следующая формула:

Относительные показатели вариации Коэффициент осцилляции Коэффициент вариации Совокупность считается однородной, а средняя величина типичной (надежной) ее характеристикой, если соблюдается условие: V≤ 33%

Относительные показатели вариации Относительное линейное отклонение Относительное квартильное отклонение или

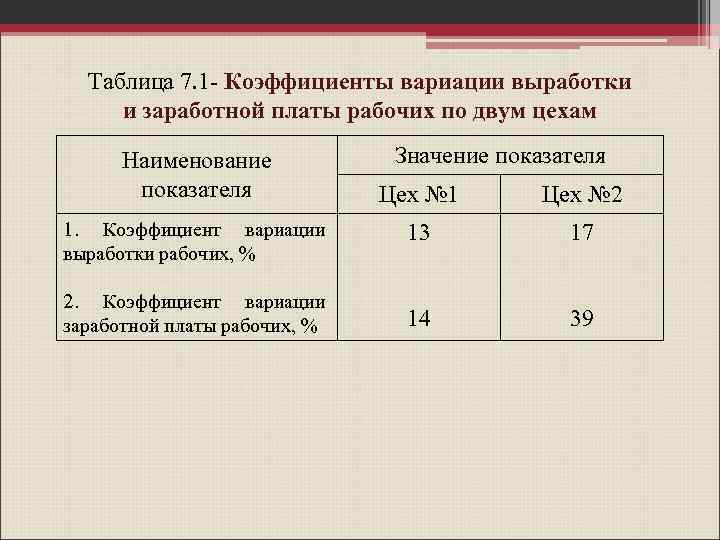Таблица 7. 1 - Коэффициенты вариации выработки и заработной платы рабочих по двум цехам Наименование показателя Значение показателя Цех № 1 Цех № 2 1. Коэффициент вариации выработки рабочих, % 13 17 2. Коэффициент вариации заработной платы рабочих, % 14 39

7. 2 Показатели вариации альтернативных признаков В ряде случаев возникает необходимость оценки вариации качественных признаков с альтернативной вариацией.

Вариация альтернативных признаков • Для оценки вариации альтернативных признаков принимают следующие допущения: ▫ наличие признака обозначается 1, ▫ а его отсутствие – 0. • Доля единиц, обладающих интересующим нас признаком, обозначается через р, доля остальных единиц составит: q = 1 – p.

Определим для этих условий среднюю величину и дисперсию: Тогда дисперсия альтернативного признака будет равна: Среднее квадратическое отклонение альтернативного признака определяется по формуле:

7. 3 Правило сложения дисперсий и его использование в статистическом анализе На основе дисперсии можно решить задачу оценки меры влияния интересующего исследователя факторного признака (x) на вариацию анализируемого результативного признака (y).

Для этого необходимо: • провести аналитическую группировку, • представить общую дисперсию результативного признака ( ) как сумму межгрупповой ( ) и средней из внутригрупповых дисперсий , • определить эмпирический коэффициент детерминации.

Правило сложения дисперсий где - общая дисперсия результативного признака (y). Она измеряет вариацию результативного признака под влиянием всех факторов, обусловивших эту вариацию; – межгрупповая дисперсия результативного признака (y), иначе ее называют факторной. Она измеряет вариацию результативного признака, обусловленную влиянием факторного признака, положенного в основу группировки; - средняя из внутригрупповых дисперсий. Оценивает вариацию результативного признака, обусловленную влиянием всех прочих факторов, исключая факторный признак, положенный в основу группировки. Иначе эту дисперсию называют остаточной.

Расчет общей дисперсии, межгрупповой и средней из внутригрупповых выполняется по формулам: - общая средняя результативного признака по всей совокупности в целом; yi – i –ое значение результативного признака; fi – частота i-го значения результативного признака. m – число групп; nj – число единиц в j-ой группе; - среднее значение результативного признака в j -ой группе. - внутригрупповая дисперсия результативного признака в j-ой группе.

• Правило сложения дисперсии позволяет определить, какая доля вариации результативного признака обусловлена влиянием факторного признака, положенного в основу группировки. • Показатель, представляющий эту долю, называют эмпирическим коэффициентом детерминации. • Корень квадратный из эмпирического коэффициента детерминации называют эмпирическим корреляционным отношением.

Эмпирическое корреляционное отношение используют для оценки тесноты связи между факторным и результативным признаками. • Эмпирический коэффициент детерминации изменяется в пределах от 0 до 1. • Если η = 0, то факторный признак, положенный в основу группировки, не оказывает влияния на результативный. • Если η = 1, то изменение результативного признака полностью объясняется влиянием факторного признака, положенного в основу группировки, а влияние прочих факторных признаков равно нулю.

• Для того, чтобы сделать более строгий вывод о существенности (несущественности) влияния того или иного факторного признака на результативный используют специальный статистический критерий: F – критерий (критерий Фишера). Если выполняется условие: Fрасч. > делают вывод, о том, что влияние факторного признака на результативный существенно или статистически значимо с доверительной вероятностью р = (1 - α).

- табличное значение F – критерия. • α – уровень значимости, который задается исследователем и обычно принимается равным 0, 05 или 0, 01. Уровень значимости указывает вероятность ошибочности вывода о существенности (несущественности) влияния факторного признака на результативный. • k 1 = m-1 и k 2 = n-m называют числом степеней свободы для межгрупповой и средней из внутригрупповых дисперсий соответственно.

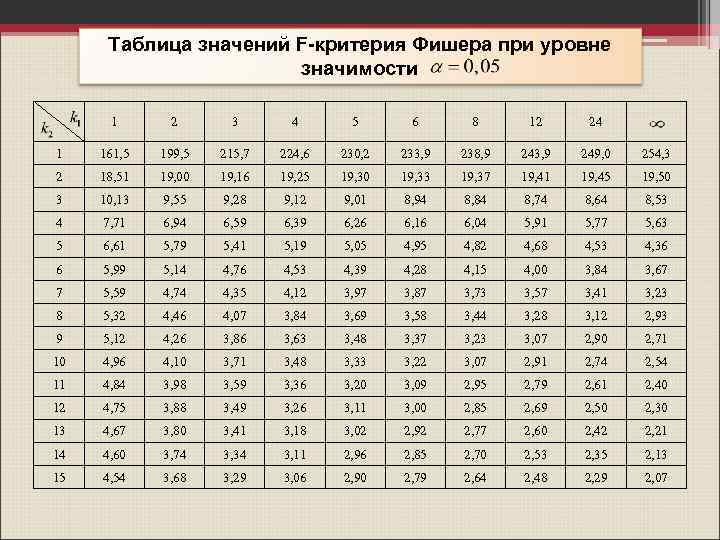Таблица значений F-критерия Фишера при уровне значимости 1 2 3 4 5 6 8 12 24 1 161, 5 199, 5 215, 7 224, 6 230, 2 233, 9 238, 9 243, 9 249, 0 254, 3 2 18, 51 19, 00 19, 16 19, 25 19, 30 19, 33 19, 37 19, 41 19, 45 19, 50 3 10, 13 9, 55 9, 28 9, 12 9, 01 8, 94 8, 84 8, 74 8, 64 8, 53 4 7, 71 6, 94 6, 59 6, 39 6, 26 6, 16 6, 04 5, 91 5, 77 5, 63 5 6, 61 5, 79 5, 41 5, 19 5, 05 4, 95 4, 82 4, 68 4, 53 4, 36 6 5, 99 5, 14 4, 76 4, 53 4, 39 4, 28 4, 15 4, 00 3, 84 3, 67 7 5, 59 4, 74 4, 35 4, 12 3, 97 3, 87 3, 73 3, 57 3, 41 3, 23 8 5, 32 4, 46 4, 07 3, 84 3, 69 3, 58 3, 44 3, 28 3, 12 2, 93 9 5, 12 4, 26 3, 86 3, 63 3, 48 3, 37 3, 23 3, 07 2, 90 2, 71 10 4, 96 4, 10 3, 71 3, 48 3, 33 3, 22 3, 07 2, 91 2, 74 2, 54 11 4, 84 3, 98 3, 59 3, 36 3, 20 3, 09 2, 95 2, 79 2, 61 2, 40 12 4, 75 3, 88 3, 49 3, 26 3, 11 3, 00 2, 85 2, 69 2, 50 2, 30 13 4, 67 3, 80 3, 41 3, 18 3, 02 2, 92 2, 77 2, 60 2, 42 2, 21 14 4, 60 3, 74 3, 34 3, 11 2, 96 2, 85 2, 70 2, 53 2, 35 2, 13 15 4, 54 3, 68 3, 29 3, 06 2, 90 2, 79 2, 64 2, 48 2, 29 2, 07

7. 4 Показатели структуры и их использование в социально-экономических исследованиях Структурные показатели распределения характеризуют особенности формы распределения и представляют значения признака, занимающих определенное место в ранжированном вариационном ряду.

Показатели структуры квантили градиенты В состав квантилей входят: медиана квартили квинтили децили перцентили

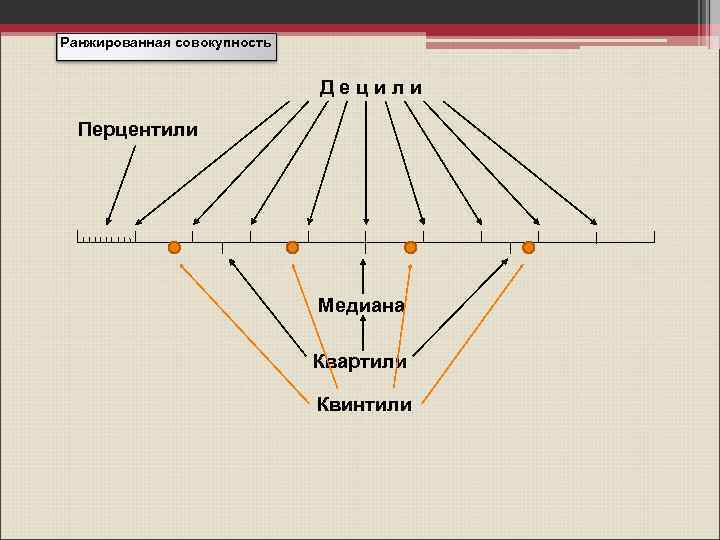Ранжированная совокупность Децили Перцентили Медиана Квартили Квинтили

Определение квартилей • Первый квартиль отделяет 1/4 часть ранжированного вариационного ряда с наименьшими значениями признака. Порядковый номер единицы совокупности, которая является носителем первого квартиля определяется как 1/4 Σf, для третьего квартиля – соответственно 3/4 Σf. • Расчет квартилей для интервального вариационного ряда выполняется по формулам:

Квантили широко используют в анализе социальноэкономических процессов, в частности для оценки дифференциации населения по уровню доходов. Например, сопоставляя девятый и первый децили, получают децильный коэффициент дифференциации: По своей сути этот коэффициент измеряет соотношение между минимальным доходом у 10% наиболее обеспеченного населения и максимальным доходом у 10% наименее обеспеченного населения.

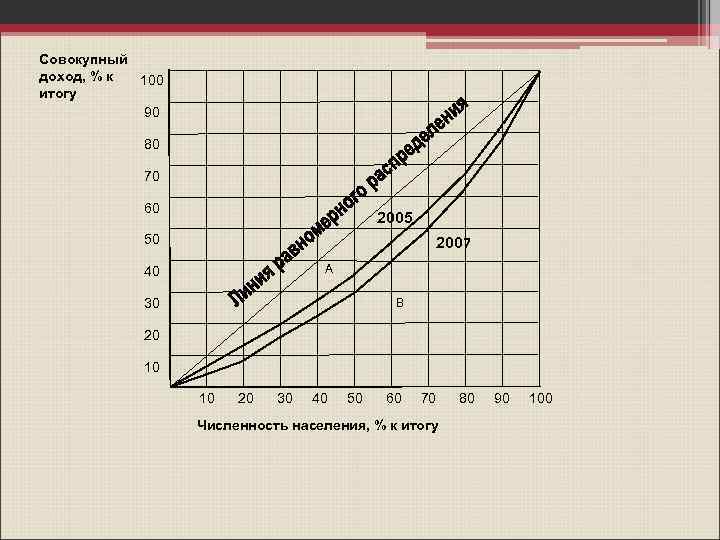Совокупный доход, % к 100 итогу 90 80 70 60 2005 50 2007 А 40 30 В 20 10 10 20 30 40 50 60 70 Численность населения, % к итогу 80 90 100