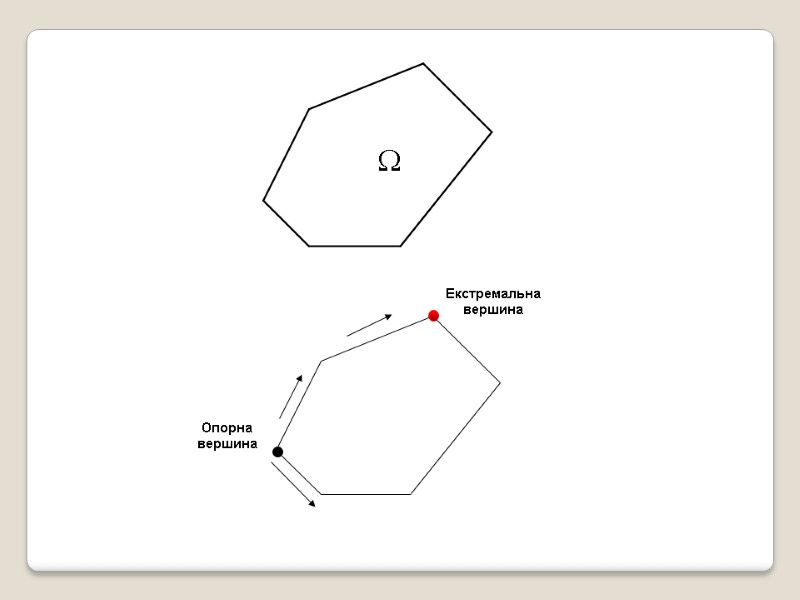
Тема 7 Симплекс-метод Ідея симплекс-методу Алгоритм знаходження початкового

Тема 7 Симплекс-метод Ідея симплекс-методу Алгоритм знаходження початкового опорного плану Алгоритм знаходження оптимального плану Приклади знаходження опорного та оптимального плану симплекс-методом

Розглянемо задачу лінійного програмування (7.1) (7.2) (7.3)

Алгоритм знаходження початкового опорного плану Складаємо початкову жорданову таблицю

Знаходимо найменше симплексне відношення:

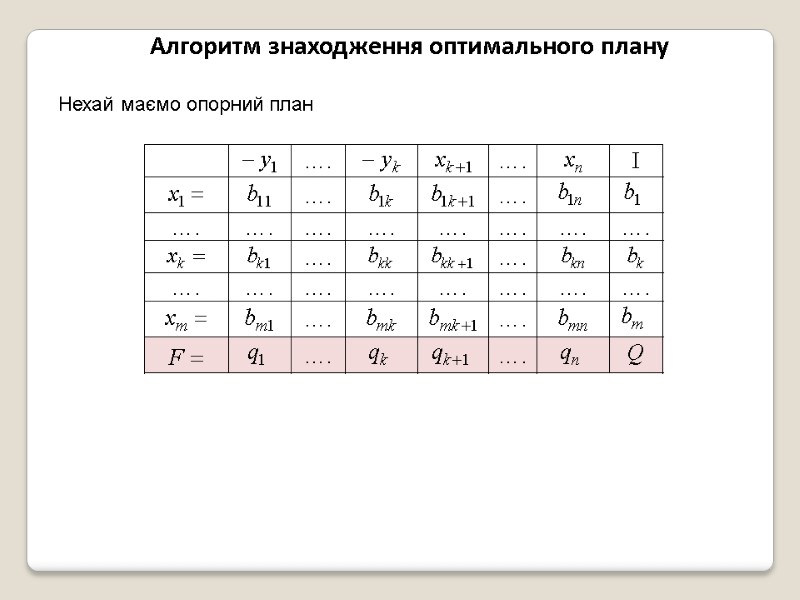Алгоритм знаходження оптимального плану Нехай маємо опорний план

Знайти будь-який опорний розв'язок системи: Складаємо початкову жорданову таблицю Для елементів другого стовпчика складаємо симплексні відношення Розв'язуючий елемент (1,2) = 2 Приклад 7.1.

З ним робимо один крок модифікованих жорданових перетворень і отримуємо таблицю Розв'язуючими стовпцями можуть бути перший або другий. Розв'язуючим елементом буде (2,2) = 1 Симплексні відношення для другого стовпчика

Робимо новий крок МЖП і отримуємо таблицю Приймаємо перший стовпчик за розв'язуючий і шукаємо в ньому розв'язуючий елемент за найменшим симплексним відношенням

Отже, елемент (3,1) = -5.5 ‑ розв'язуючий, з ним і робимо новий крок МЖП і отримаємо таблицю В отриманій таблиці вільні члени невід'ємні і опорним є план Опорний план надає наступні значення шуканим величинам:

Приклад 7.2 Знайти максимум функціоналу: при виконанні обмежень: та умовах невід’ємності

Приведемо систему обмежень до виду: Складемо початкову симплекс-таблицю Знаходимо симплексні відношення

Візьмемо розв’язуючий елемент із стрічки з від’ємним вільним членом (тобто –1), щоб на слідуючому етапі отримати там додатнє число. Зробивши один крок МЖВ, отримаємо таблицю В першій стрічці отримали вільний член, рівний нулю, тобто маємо виродження. Якщо б у попередній таблиці за розв’язуючий елемент взяти елемент з першої стрічки, то вільний член в третій стрічці став би рівний нулю, тобто знову мали б виродження. При неоднозначності вибору розв’язуючого елемента так буде завжди.

Приклад 7.3 Знайти максимум функціоналу при обмеженнях та умовах невід’ємності

Приведемо систему нерівностей до виду Складемо початкову симплекс-таблицю Шукаємо симплексні відношення для другого стовпчика: За розв’язуючий візьмемо елемент (3,2) = -1 та виконаємо один крок МЖВ.

В результаті отримаємо таблицю Шукаємо симплексні відношення для першого стовпчика: За розв’язуючий візьмемо елемент (2,1) = 6 та виконаємо один крок МЖВ.

Оптимальний план: Функціонал приймає найбільше значення В результаті отримаємо таблицю