Тема6.ppt
- Количество слайдов: 36

Тема 6 Поисковые деревья. Базовые операции

Бинарные поисковые деревья o o o поиск по ключу (поиск минимального, максимального); добавление элемента с заданным ключом; удаление элемента с заданным ключом. Если бинарное поисковое дерево “вытянуто” в список, то высота дерева h = n, n – количество вершин дерева. Если бинарное поисковое дерево является сбалансированным, то h=log 2 n. Трудоемкость операций – O(h) : n n o O(n)- в худшем, O(log 2 n) – в худшем для сбалансированных деревьев. Минимальный (максимальны элемент бинарного поискового дерева соответствует ключевому значению самой левой (правой) вершины дерева. 2

Добавление элемента (поиск по дереву с включением) o Трудоемкость в худшем есть O(h). Процедура добавления элемента может бы использована для n построения поискового дерева (необходимо n раз вызвать эту процедуру для каждого элемента из последовательности поступающих на вход ключей. Трудоемкость построения бинарного поискового дерева есть O(nh). n сортировки последовательности из n ключей. Для этого необходимо построить для последовательности поступающих ключей бинарное поисковое дерево совершит его внутренний обход. Трудоемкость алгоритма сортировки последовательности ключей есть O(nh). o 3

Удаление элемента с заданным ключом x o o o o Сначала определяем вершину дерева v с ключевым значением key(v) = x. Если найденная вершина имеет более одного сына, то ее удаление из дерева производится очевидны образом (как это традиционно выполняется списковой структуре, когда для удаляемого элемента известен предыдущий и следующий элементы. Трудности с удалением возникают в ситуации, когда у удаляемой вершины v два сына. В этом случае ключевое значение x вершины v нужно заменить либо на максимальный ключ key(wl) в левом поддереве для вершины v, либо на минимальным ключ key(wr) в правом поддереве для вершины v. Затем происходит удаление соответствующей вершины wl или wr Очевидно, что каждая из указанны вершин wl или wr, имеет более одного сына. Трудоемкость процедур удаления элемента с заданным ключом есть O(h). 4

Сбалансированные деревья o o Одним из инвариантов (свойств) сбалансированных поисковых деревьев является свойство сбалансированности по высоте. АВЛ-дерево это бинарное поисковое дерево, у которого для каждой вершины v высота поддерева, корнем которого является левый сын вершины v, отличается не более чем на единицу от высоты поддерева, корнем которого является правый сын вершины v. Т 0 Т 1 Т 2 Т 3 5

Теорема. Пусть n – число внутренних вершин АВЛ-дерева, h – его высота. Тогда справедливы следующие неравенства: log (n + 1) ≤ h< 1. 4404 · log (n + 2) – 0. 328 (1) Доказательство: o Так как АВЛ-дерево является бинарным деревом, то может содержать более, чем 2 h - 1 внутренних вершин. Поэтому n ≤ 2 h -1; h ≥ log(n+1). o Определим теперь минимальное количество внутренних вершин для АВЛ-дерева высоты h. Обозначим через Th АВЛ-дерево высоты h с минимальным числом внутренних вершин. o Так как принцип построения деревьев напоминает построение чисел Фибоначчи, то такие деревья обычно называют деревьями Фибоначчи. o 6

o Пусть Nh – количество внутренних вершин в дереве Th. Тогда Nh+1 = Nh-1 + Nh + 1. Сделаем замену переменных F’h = Nh + 1, тогда выражение F’h+1 = F’h + F’h– 1 соответствует числам Фибоначчи. Если Fi – i-oe число Фибоначчи, то o Найдем соответствие между Fi и F’h. Так как Fi = F’h при i = 2 + h, то o o o h 1 2 3 4 … N 1 2 4 7 … F’h= Nh + 1 2 3 5 8 … Fi – числа Фибоначчи 1 1 2 3 5 5 i=1 i=2 i=3 i=4 i=5 i=6 7 …

Поэтому, в силу того, что Nh = F’h – 1 и имеем Логарифмируя, получаем правую часть выражения (1). o Из теоремы следует, что для АВЛ-дерева с n вершинами высота h = O(log 2 n). Поэтому все базовые операции можно выполнить за время O(log 2 n). 8

Базовые операции с АВЛ деревьями. Добавление вершины с заданным ключом o o o Проходим по пути поиска, пока не определим место добавления вершины с заданным ключом. Добавляем новую вершину и определяем произошла ли вдоль пути поиска разбалансировка. Если произошла разбалансировка, то выполнить процедуру, восстанавливающую нарушенный инвариант. 9

Процедуры восстановления инварианта после выполнения операции добавления нового элемента. 1 -й случай: o o Пусть k 2 – вершина максимальной глубины для которой произошла разбалансировка после выполнения операции добавления нового элемента (z – отец вершины k 2) o Очевидно, что все вершины для которых нарушился инвариант лежат на пути от корня до вершины k 2. И пусть для вершины k 2 выполняется: n n высота ее левого поддерева больше высоты ее правого поддерева на 2, это происходит потому, что балансировка происходит после каждой операции добавления удаления и максимально возможная разность высот поддеревьев для каждой вершины не превышает 2, так как перед выполнением этой операции она не превышала 1. у левого сына k 1 вершины k 2 высота левого поддерева больше высоты правого поддерева (это соответствует добавлению элемента в поддерево корнем которого является левый сын вершины k 1). 10

o o o а) фрагмент дерева до выполнения процедуры добавления элемента в дерево А, б) нарушение инварианта для вершины k 2 после выполнения процедуры добавления вершины в дерево, в) LL-поворот, который необходимо выполнить, чтобы для вершины k 2 выполнился нарушенный инвариант (поддеревья обозначены прямоугольниками, вершины – кругами). z a) h-1 h-2 h z б) h k 2 k 1 C A B h-3 h-3 h-1 h-2 h+1 k 2 k 1 A z в) h-1 C B h-3 h k 1 h-3 h-2 A k 2 h-2 B C h-3 11

После выполнения LL-поворота высоты всех вершин, для которых было возможно нарушение инварианта остались такими же как и до выполнения процедуры добавления. И поэтому для них выполняется свойство сбалансированности по высотам, так как оно выполнялось до того как произошла разбалансировка. o Следовательно, LL-поворот приводит к сбалансированности по высотам всех вершин дерева. Алгоритм LL-поворот : { k 1 ← k 2. left; // k 1 – является левым сыном вершины k 2. left ← k 1. right; // левым сыном k 2 становится правый сын верш. k 1. right ← k 2; // правым сыном k 1 становится вершина k 2 z ← k 1; // отцом вершины k 2 становится вершина k 1 } o 12

2 -й случай: o Пусть k 2 - вершина максимальной глубины для которой произошла разбалансировка в результате выполнения операции добавления нового элемента и для которой: n n высота правого поддерева вершины k 2 больше высоты ее левого поддерева на 2, у правого сына k 1 вершины k 2 высота его правого поддерева больше высоты его левого поддерева (происходило добавление вершины в дерево, корнем которого является правый сын вершины k 1). 13

o o а) нарушение инварианта для вершины k 2 после выполнения процедуры добавления вершины в дерево С, б) RR-поворот, который необходимо выполнить, чтобы для вершины k 2 выполнился нарушенный инвариант (поддеревья обозначены прямоугольниками, вершины – кругами). z а) h h+1 z б) k 2 h-1 h-3 A k 1 h-1 B C h-3 h-2 h-3 h k 1 k 2 A C h-2 Алгоритм RR-поворот : { k 1 ← k 2. right; k 2. right ← k 1. left; k 1. left ← k 2; z ← k 1; } B h-3 h-2 14

3 -й случай: o Пусть k 2 – вершина максимальной глубины для которой произошло нарушение инварианта в результате выполнения операции добавления нового элемента и для которой: n высота правого поддерева вершины k 2 больше высоты ее левого поддерева на 2, n у правого сына k 1 вершины k 2 высота его левого поддерева больше высоты его правого поддерева. 15

o o o а) фрагмент дерева до выполнения процедуры добавления элемента в дерево В, б) нарушение инварианта для вершины k 2 после выполнения процедуры добавления, в) RL-поворот, который необходимо выполнить, чтобы для вершины k 2 выполнился нарушенный инвариант. z a) h-3 k 1 А k 1 h-2 h-3 h-4 В k 3 С h-4 h-2 D h-3 В h h-1 k 3 h-1 А z в) h+1 k 2 h-1 z б) h k 3 С h-4 D h-3 h-2 А h-2 k 2 В h-3 k 1 С h-4 D h-3 16

Алгоритм RL-поворот: { k 1 ← k 2. right; // k 1 – является правым сыном вершины k 2 k 3 ← k 1. left; // k 3 – является левым сыном вершины k 1 k 2. right ← k 3. left; // правым сыном k 2 становится левый сын k 3 k 1. left ← k 3. right; // левым сыном k 1 становится правый сын k 3. left ← k 2; // левым сыном k 3 становится k 2 k 3. right ← k 1; // правым сыном k 3 становится k 1 z ← k 3; // отцом вершины k 2 становится вершина k 3 } 17

4 -й случай: o Пусть k 2 – вершина максимальной глубины для которой произошло нарушение инварианта в результате выполнения операции добавления нового элемента и для которой: n высота левого поддерева вершины k 2 больше высоты ее правого поддерева на 2, n у левого сына k 1 вершины k 2 высота его правого поддерева больше высоты его левого поддерева. 18

а) нарушение инварианта для вершины k 2 после выполнения процедуры добавления, б) LR-поворот, который необходимо выполнить, чтобы для вершины k 2 выполнился нарушенный инвариант. o o z a) h h-1 h+1 k 2 k 1 D h-3 h-2 С h-3 h-2 k 1 k 3. left ← k 1; z ← k 3; k 2 } А В h-3 В h-4 h h-1 k 3 h-2 А z б) Алгоритм LR-поворот: { k 1 ← k 2. left; k 3 ← k 1. right; k 2. left ← k 3. right; k 1. right ← k 3. left; k 3. right ← k 2; С h-4 h-3 D h-3 19

Удаление вершины с заданным ключом o Осуществляем поиск и удаление вершины с заданным ключом. n n o Определяем произошла ли вдоль пути поиска разбалансировка. n o процедура аналогична процедуре удаления для бинарного поискового дерева. Рассматриваются варианты: удаляемый элемент имеет не более одного сына; удаляемый элемент имеет двух сыновей. Нарушение инварианта могло произойти только для вершин на пути поиска, так как высоты только этих вершин могли уменьшиться на 1. Следует отметить, что если высота вершины уменьшилась на 1, то для нее выполняется свойство сбалансированности по высотам. 20

o o Пусть k 2 – вершина для которой нарушился инвариант (высота вершины k 2 после выполнения процедуры удаления не изменилась, т. к нарушение инварианта для нее произошло только при удалении вершины из поддерева вершины k 2 меньшей высоты). Если произошла разбалансировка, то выполнить процедуру восстанавливающую нарушенный инвариант для вершины k 2 (z отец вершины). n n После выполнения балансировки для вершины k 2, могла произойти разбалансировка для вершины на пути от корня до вершины z. Находим опять вершину на максимальной глубине для которой произошло нарушение инварианта и выполняем балансировку для нее. 21

Процедуры восстановления инварианта после выполнения операции удаления элемента. 1 -й случай: o Пусть k 2 – вершин для которой произошла разбалансировка. n n 1. высота ее левого поддерева больше высоты ее правого поддерева С на 2 (происходило удаление вершины из дерева С), у левого сына k 1 вершины k 2 высота левого поддерева А больше или равна высоте правого поддерева В. Рассмотрим сначала ситуацию, когда высоты деревьев А и В равны. 22

o o o а) фрагмент дерева до выполнения процедуры удаления вершины из дерева С, б) нарушение инварианта для вершины k 2 после выполнения процедуры, в) LL-поворот, который необходимо выполнить, чтобы для вершины k 2 выполнился нарушенный инвариант. a) z h z k 2 h-1 б) k 1 h C A B h-2 h-2 h-1 h-2 k 1 A z в) h C B h-2 k 1 h-3 h-2 A k 2 h-1 B C h-2 h-3 23

Рассмотрим ситуацию, когда высота дерева А больше высоты дерева В. а) фрагмент дерева до выполнения процедуры удаления вершины из дерева С, б) нарушение инварианта для вершины k 2 после выполнения процедуры, в) LL-поворот, восстанавливающий инвариант. 2. o o o a) z h z k 2 h-1 б) k 1 h C A B h-2 h-3 h-2 h-1 h-2 в) k 2 k 1 A h-1 C B h-3 h z k 1 h-3 h-2 A k 2 h-2 B C h-3 24

2 -й случай: o Пусть k 2 – вершин для которой произошла разбалансировка. n n 1. высота ее правого поддерева больше высоты ее левого поддерева А на 2 (происходило удаление вершины из дерева А), у правого сына k 1 вершины k 2 высота правого поддерева C больше или равна высоте левого поддерева В. Пусть высота дерева С больше высоты дерева В. 25

o RR-поворот. z а) h б) h k 2 h-2 A k 1 h-1 z в) z h-1 k 2 h-3 A k 1 h-1 B C h-3 h-2 h-2 h k 1 k 2 A h-3 C h-2 B h-3 26

2. Пусть высоты деревьев В и С равны. o RR-поворот. z а) h б) h k 2 h-2 A k 1 h-1 z в) z k 1 h k 2 h-3 A k 1 h-1 B C h-2 h-2 h-1 k 2 A h-3 C h-2 B h-2 27

3 -й случай: o Пусть k 2 – вершин для которой произошла разбалансировка. n n высота ее правого поддерева больше высоты ее левого поддерева А на 2 (происходило удаление вершины из дерева А), у правого сына k 1 вершины k 2 высота левого поддерева больше высоты его правого поддерева. 28
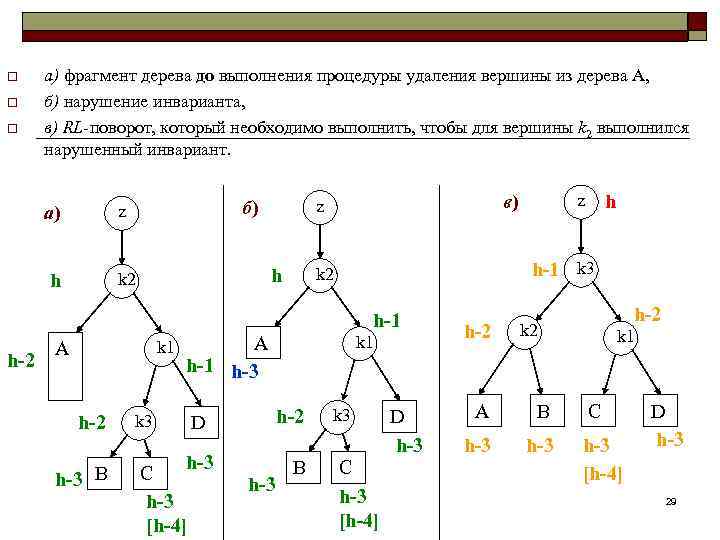
o o o а) фрагмент дерева до выполнения процедуры удаления вершины из дерева А, б) нарушение инварианта, в) RL-поворот, который необходимо выполнить, чтобы для вершины k 2 выполнился нарушенный инвариант. z h k 2 h-1 h-2 k 1 А k 1 h-3 А h-2 h-3 В k 3 h-2 D h-3 С h-3 [h-4] h-3 В h h-1 k 3 k 2 h z в) z б) a) k 3 С h-3 [h-4] D h-3 h-2 k 2 А В h-3 k 1 С h-3 [h-4] D h-3 29

4 -й случай: o Пусть k 2 – вершин для которой произошла разбалансировка. n n высота ее левого поддерева больше высоты ее левого поддерева D на 2 (происходило удаление вершины из дерева D), у левого сына k 1 вершины k 2 высота правого поддерева больше высоты его левого поддерева. 30

а) фрагмент дерева до выполнения процедуры, б) нарушение инварианта, в) LR-поворот. o o o h h-1 h k 2 h-1 k 1 D h-2 k 3 h-2 А z б) z a) k 2 k 1 D h-3 В h-3 С h-3 [h-4] В h-4 h-2 С h-3 [h-4] h-2 k 1 А В h-3 h-3 h h-1 k 3 h-2 А z в) h-3 k 2 С h-3 [h-4] D h-3 31

Базовые операции для красно-черных деревьев Удалить элемент. Трудоемкость О(lg n) (аналогично добавлению). Добавить элемент. Трудоемкость О(lg n). o o n n Сначала мы применяем процедуру добавления, как делалось для бинарных поисковых деревьев, и красим новую вершину в красный цвет. Вставив красный узел, мы сохраняем свойство черной высоты (свойство 4). Но может оказаться так, что предок нового узла – красный: при этом будет нарушено свойство 3. Для восстановления RB-свойства приходится перекрасить некоторые вершины и произвести вращения. При этом возможны различные ситуации. 32

1. Красный предок, красный "дядя": 1. o o У нового узла предок и "дядя" оказались красными. Простое перекрашивание избавляет нас от красно-красного нарушения. После перекраски нужно проверить "дедушку" нового узла, поскольку он может оказаться красным. Обратите внимание на распространение влияния красного узла на верхние узлы дерева. Если в самом конце корень был красным, а нам надо его перекрасить в черный цвет, то в этом случае увеличивается черная высота дерева. 33

34

2. Красный предок, черный "дядя": o Другой вариант красного нарушения "дядя" нового узла оказался черным. Здесь узлы может понадобиться вращать, чтобы скорректировать поддеревья. RL-вращение 35

o В этом месте алгоритм может остановиться из-за отсутствия красно-красных конфликтов и предок окрашивается в черный цвет. o Обратите внимание, что если узел X был в начале правым потомком, то первым применяется левое вращение, которое делает этот узел левым потомком. 36
Тема6.ppt