Тема 6 Моделирование по схеме марковских случайных процессов

Тема 6. Моделирование по схеме марковских случайных процессов. Системы массового обслуживания Простейший или стационарный пуассоновский поток событий. Марковские случайные процессы. Уравнения Колмогорова для вероятностей состояния, предельные вероятности. Метод динамики средних. Полумарковские процессы. Лекция 13

Простейший или стационарный пуассоновский поток событий • Стохастической системой называется система, в которой наблюдаются события, проявляющиеся случайным образом. • Случайный процесс, протекающий в стохастической системе, представляет собой последовательность событий, заключающихся в ее переходе из одного состояния в другое в случайные моменты времени или же в неизвестное заранее состояние. • Возможные состояние системы обозначаются Х 1, Х 2, Х 3 …, Хn. • Число возможных состояний системы может быть как конечным (дискретным), так и бесконечным. • Состояния системы и возможные переходы из одного состояния в другое для наглядности изображаются в виде схемы, называемой графом состояний, где стрелками показаны переходы системы из одного состояния в другое. • Последовательность событий в системе в некоторые моменты времени называется потоком событий. При исследовании стохастических систем с большой степенью достоверности принято представление о потоке событий в ней как о простейшем или стационарном пуассоновском потоке.

Свойства и характеристики стационарного пуассоновского потока событий • Простейший поток обладает тремя основными свойствами: отсутствие последействия, ординарность и стационарность. • При пуассоновском потоке событий вероятность появления за промежуток времени τ ровно k-событий равна: где α - математическое ожидание числа событий за промежуток времени . Параметр α на отрезке времени 0…τ связан с интенсивностью (или плотностью) потока событий λ(t) соотношением: λ(t) - это математическое ожидание числа событий за единицу времени. Для стационарного потока событий

Свойства и характеристики стационарного пуассоновского потока событий Для стационарного пуассоновского потока закон распределения длины промежутка времени между соседними событиями (времени ожидания события) является показательным и функция плотности вероятности имеет вид: Математическое ожидание времени между появлениями двух соседних событий определяется: Главной задачей при изучении случайных процессов в стохастических системах является определение вероятностей Pi(t) нахождения системы во всех возможных состояниях Xi(i=1, …, n) для любого момента времени t.

Виды стохастических систем • В практике эксплуатации авиационных систем наиболее часто встречаются системы дискретного типа с дискретным или непрерывным временем. • Системы дискретного типа с дискретным временем - переход системы в другое состояние осуществляется только в фиксированные моменты времени; в промежутках же между этими моментами система изменить состояние не может. • Системы дискретного типа с непрерывным временем - переход системы из состояния в состояние возможен в любой момент времени. Переход является случайным событием.

Марковский случайный процесс Допущения о пуассоновском характере потока событий и о показательном времени нахождения системы в различных состояниях позволяют применить аппарат марковских процессов. Случайный процесс называется марковским (или процессом без последствия), если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящий момент времени и не зависит от того, каким образом она пришла в это состояние. Последовательность событий в системе при вышеуказанных допущениях образует марковскую цепь. Интенсивность потока событий для марковского процесса обозначается λij и является интенсивностью переходов системы из i-го состояния в j–ое состояние. Марковская цепь может быть однородной и неоднородной. Если интенсивности переходов не зависят от времени, то цепь является однородной, в противном случае – неоднородной.

Марковский случайный процесс В реальных стохастических системах наиболее часто встречаются марковские процессы с конечным числом состояний и непрерывным временем. Такой процесс называется непрерывной цепью Маркова. Обозначим через рi(t) вероятность того, что в момент времени t система будет находиться в состоянии Xi(i=1, 2, …, n). Сумма вероятностей рi(t) для любого t будет равна =1, как вероятность суммы полной группы несовместных событий Переход системы из одного состояния в другое происходит случайным образом и характеризуется вероятностью перехода. Вероятностью перехода Pij(t, t+ t) называется условная вероятность того, что находясь в момент времени t в состоянии Xi, система за время t окажется в состоянии Xj:

Марковский случайный процесс Для марковского случайного процесса вероятность любого события в будущем не зависит от предыстории, а это означает, что вероятность перехода не зависит от t, то есть количества времени, которое система провела в состоянии Xi. В итоге вероятность перехода определяется как вероятность того, что за время t появится событие, переводящее систему из состояния Xi в состояние Xj. Для достаточного малого значения t эта вероятность пропорциональна значениям t и интенсивности переходов ij: Марковский процесс, протекающий в системах со счетным множеством состояний и непрерывным временем, можно описать с помощью обыкновенных дифференциальных уравнений, в которых неизвестными функциями являются вероятности состояний р1(t), р2(t), …, рn(t)

Уравнения Колмогорова для вероятностей состояния Пусть система имеет n возможных состояний: Х 1, Х 2, …, Хn и известны интенсивности переходов ij системы из одного состояния в другое. Процесс смены состояний является марковским. Определим вероятность рk(t) пребывания системы в k-ом состоянии для произвольного момента времени. 1. Определим вероятность рk(t+ t) того, что система в момент времени (t+ t) окажется в состоянии Хк t t+ t X 1 X 2 … Xk … Xn Xk рi(t) - вероятность того, что в момент времени t система находится в состоянии Xi рik( t) – условная вероятность перехода системы за время t из состояния Xi в состояние Xk рkk( t) - вероятность того, что система за время t была и остается в состоянии Xk.

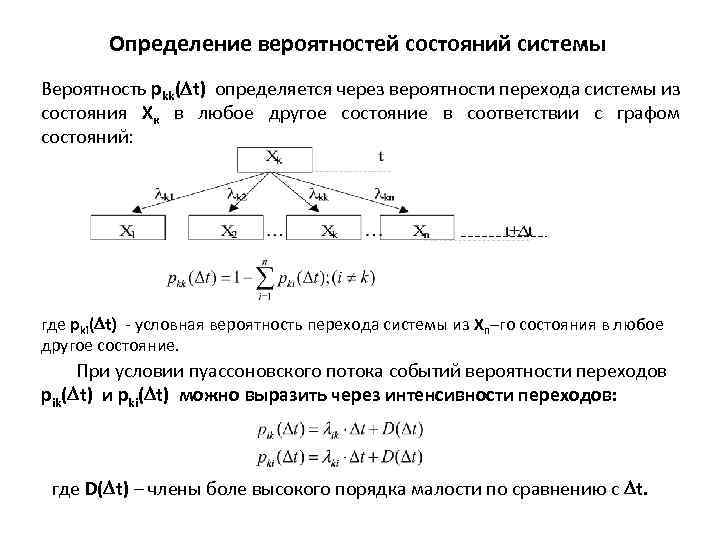Определение вероятностей состояний системы Вероятность рkk( t) определяется через вероятности перехода системы из состояния Хк в любое другое состояние в соответствии с графом состояний: где рki( t) - условная вероятность перехода системы из Xn–го состояния в любое другое состояние. При условии пуассоновского потока событий вероятности переходов рik( t) и рki( t) можно выразить через интенсивности переходов: где D( t) – члены боле высокого порядка малости по сравнению с t.

Определение вероятностей состояний системы Если перенести рk(t) в левую часть и разделить обе части выражения на t, то получим:

Уравнения Колмогорова для вероятностей состояния Переходя к пределу при t 0 будем иметь линейное дифференциальное уравнение для вероятности рk(t) Из полученного уравнения, записанного для всех n возможных состояний системы составляется система уравнений, решение которой дает искомые выражения вероятностей состояний системы р1(t), р2(t), …, рn(t). Система дифференциальных уравнений интегрируется, например при следующих начальных условиях: стохастическая система в начальный момент времени t 0 находится в -ом состоянии, тогда При t=t 0; р (t 0)=1; рk (t 0)=0, k=1, 2, …n, k Для снижения порядка системы используется очевидное соотношение

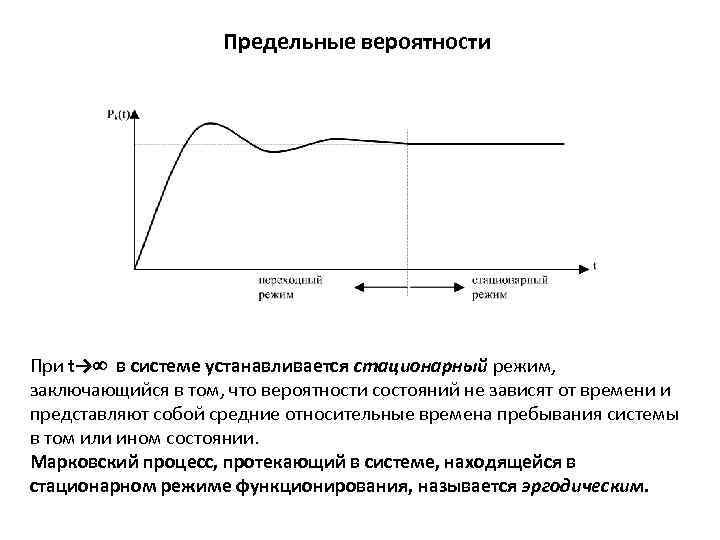Предельные вероятности При t→ в системе устанавливается стационарный режим, заключающийся в том, что вероятности состояний не зависят от времени и представляют собой средние относительные времена пребывания системы в том или ином состоянии. Марковский процесс, протекающий в системе, находящейся в стационарном режиме функционирования, называется эргодическим.

Предельные вероятности Чтобы определить предельные вероятности, необходимо все производные в уравнениях системы приравнять к нулю, а также иметь в виду, что pk(t)=pk Эта система решается при начальных условиях: p 1(0)=1; pk(0)=0; k=2, 3, …, n, а также при известных значениях интенсивностей передов ij

Метод динамики средних Достаточно часто встречаются системы, состоящие из большого числа однородных элементов, каждый из которых может находиться в нескольких состояниях, а интенсивности переходов в различные состояния ik(t) зависят от числа элементов, находящихся в данном состоянии. Для анализа таких стохастических систем применяются менее точные, но и менее трудоемкие методы, в частности метод динамики средних. Этот метод позволяет определить для любого момента времени t распределение в среднем числа элементов системы по возможным состояниям, т. е. решается задача прогнозирования среднего числа элементов в каждом состоянии. Рассмотрим систему, которая состоит из большого числа N элементов, каждый из которых может находиться в n возможных состояниях. Обозначим среднее число элементов, находящихся в состоянии Xk, через mk(t), которое можно определить через вероятности этого состояния.

Метод динамики средних Вероятность pk(t) для любого момента времени t определяется из системы дифференциальных уравнений вида Так как Систему можно записать в виде предварительно умножив обе части уравнений на N: Полученные уравнения, решениями которых являются средние численности элементов mk(t), называются уравнениями динамики средних.

Полумарковские процессы Если игнорировать случайный характер времени ожидания и рассматривать только моменты перехода, то процесс S(t) будет представлять собой однородную цепь Маркова. Если распределение случайного времени ожидания является экспоненциальным, т. е. поток является пуассоновским, то имеет место чисто марковский процесс с дискретными состояниями и непрерывным временем. Если же распределение времени ожидания является любым другим (кроме экспоненциального), в том числе это время может быть и некоторым постоянным числом, то процесс не является марковским в чистом виде. Si SK S 2 S 1 Si Se . . . Случайный процесс, при котором переходы между состояниями являются Марковскими, а времена нахождения в любом из состояний описываются произвольной функцией распределения, называется полумарковским.