Тема 6 МАТЕМАТИЧНІ ОСНОВИ ЛІНІЙНОГО ПРОГРАМУВАННЯ Жорданові перетворення

Тема 6 МАТЕМАТИЧНІ ОСНОВИ ЛІНІЙНОГО ПРОГРАМУВАННЯ Жорданові перетворення Обчислення оберненої матриці за допомогою модифікованих жорданових перетворень Розв’язування СЛАР методом жорданових перетворень

Із системою лінійних рівнянь зіставляємо таблицю Метод жорданових перетворень

Алгоритм жорданових перетворень розв’язуючий елемент 3. Всі елементи розв’язуючого рядка ділимо на розв’язуючий елемент і міняємо знак (крім розв’язуючого елемента). 4. Всі елементи розв’язуючого стовпчика ділимо на розв’язуючий елемент. 1. Обираємо будь-який 2. Розв’язуючий елемент замінюємо оберненим 5. Решта елементів таблиці переховуємо за «правилом визначника» 6. Міняємо місцями символи та

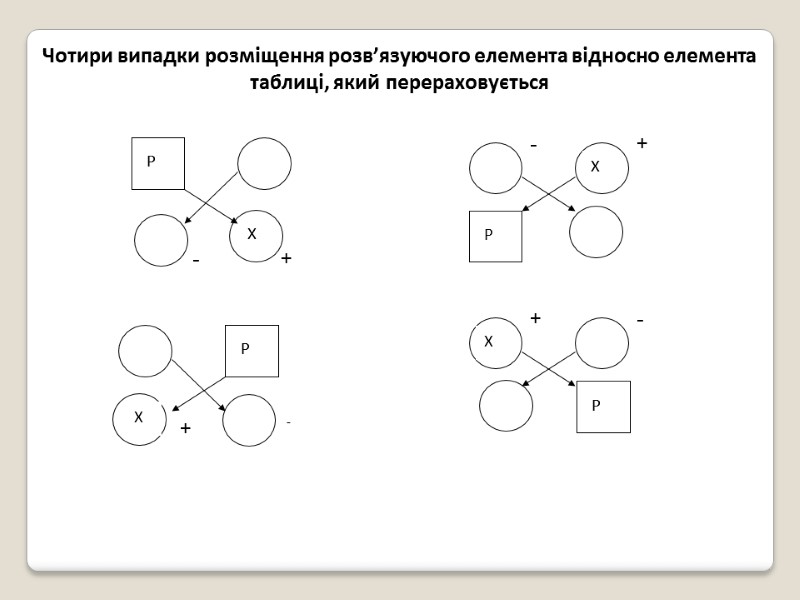Чотири випадки розміщення розв’язуючого елемента відносно елемента таблиці, який перераховується

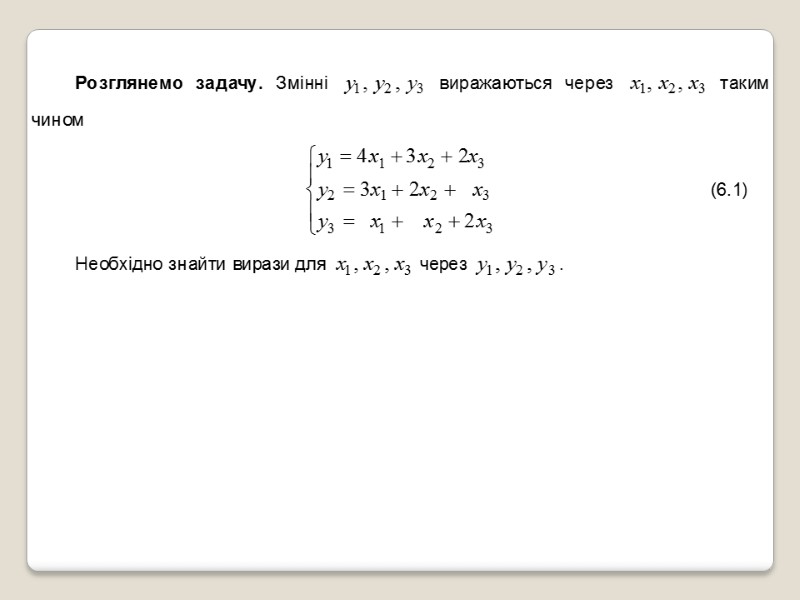
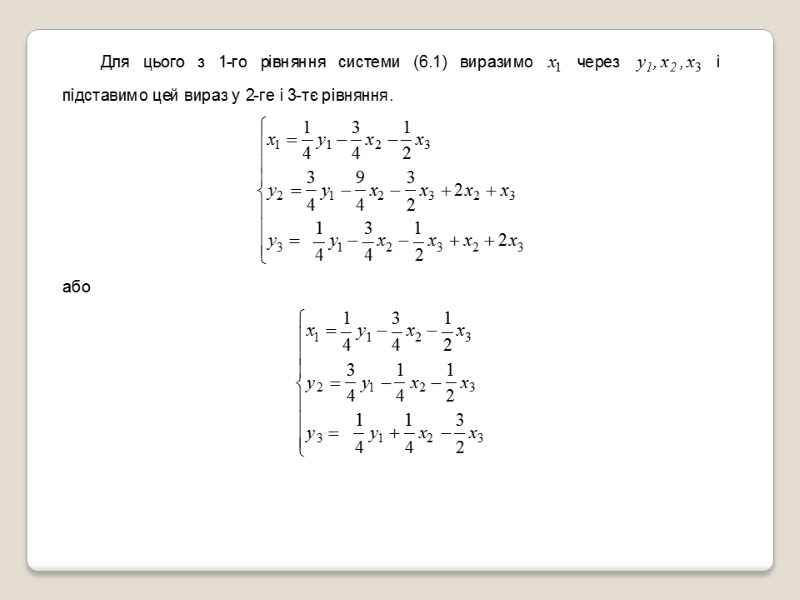
Вихідна система Відповідна таблиця Виконаємо кроки жорданових перетворень

Записавши згідно останньої таблиці систему, отримаємо

Алгоритм модифікованих жорданових перетворень 3. Всі елементи розв’язуючого рядка ділимо на розв’язуючий елемент. 4. Всі елементи розв’язуючого стовпчика ділимо на розв’язуючий елемент і міняємо знак .

Обчислення оберненої матриці за допомогою модифікованих жорданових перетворень Запишемо умову вихідної задачі у матричному вигляді Перетвореній системі відповідає рівність , де тобто

Правило обчислення оберненої матриці за допомогою жорданових перетворень 3.

Розв’язання систем лінійних рівнянь методом жорданових перетворень Побудуємо жорданову таблицю Проведемо жорданові перетворення

Отже, розв’язки системи: