ТЕМА 5 ТРАНСПОРТНЫЕ СЕТИ 1 Основные понятия и

ТЕМА 5. ТРАНСПОРТНЫЕ СЕТИ 1. Основные понятия и определения 2. Задача о максимальном потоке. Алгоритм Форда-Фалкерсона 3. Транспортная задача

1 Основные понятия и определения Транспортной сетью называется ориентированный связный мультиграф без петель, в котором: v существует одна и только одна вершина x 0, называемая входом сети, что v существует одна и только одна вершина хn, называемая выходом сети, что v каждой дуге (x. I хj) графа отнесено целое число Cij называемое пропускной способностью дуги. Вершина x 0 является источником, а вершина хn – стоком. Величина Cij характеризует максимальное количество груза, который соответствующая коммуникация может пропустить за единицу времени.

Поток φij характеризует количество груза, перемещаемого в единицу времени из пункта i в пункт j. . Из физических соображений возникают следующие ограничения на числа φij : 1) Поток по любому ребру не может быть больше его пропускной способности, т. е. 2) в каждой вершине, не являющейся ни источником ни стоком, количество прибывающего вещества должно быть равно количеству отправляющегося: 3) поток, выходящий из источника x 0, в точности равен потоку, входящему в сток хn , т. е.

Величина называется величиной потока транспортной сети. Если поток по дуге (x. I хj) равен ее пропускной способности, то такая дуга называется насыщенной. Путь из х0 в хn называется насыщенным, если он содержит хотя бы одну насыщенную дугу. Поток, насыщающий все пути из х0 в хn, называется полным. Наибольший из полных потоков называется максимальным. Для исследования распределения потока по дугам сети вводят понятие разреза транспортной сети.

Пусть все вершины транспортной сети разбиты на два так, что непересекающихся подмножества R и Разрезом, отделяющим х0 от хп , называется совокупность всех дуг (xi, xj), которые исходят из вершин , заканчиваются в вершинах и при удалении которых из сети блокируются все пути из источника в сток. Пропускная способность разреза численно равна сумме пропускных способностей дуг, его образующих, т. е. Любой путь из источника в сток содержит хотя бы одну дугу разреза , именно поэтому при удалении дуг какого-либо разреза, все пути из источника в сток прерываются.

Вершина х0 является входом сети (источник), а вершина x 5 является выходом сети (сток). Числа, приписанные дугам и ребрам, означают их пропускные способности. Разрез транспортной сети (х1 х3; х2 х4) В каждой сети существует некоторое множество разрезов.

2 Задача о максимальном потоке. Алгоритм Форда-Фалкерсона С математической точки зрения задача о максимальном потоке формулируется следующим образом: При заданной конфигурации сети и известной пропускной способности Cij найти неотрицательные значения φij удовлетворяющие условиям и и максимизирующие функцию φ , т. е.

Алгоритм для нахождения максимального потока был предложен Фордом и Фалкерсоном и заключается в постепенном увеличении потока, пропускаемого по сети, до тех пор, пока он не станет наибольшим. Алгоритм основан на теореме Форда-Фалкерсона: В любой транспортной сети максимальный поток из источника х0 в сток хn, равен минимальной пропускной способности разреза, отделяющего х0 от хn. Алгоритм состоит из подготовительного этапа и конечного числа шагов, на каждом из которых происходит допустимое увеличение потока.

1. На подготовительном этапе формируется матрица пропускных способностей дуг сети. Если пропускная способность дуги (xi хj) больше нуля, а пропускная способность симметричной ей дуги равна нулю, то в клетку (i, j) заносится элемент Cij, а в клетку (j, i) - нуль. 2. Находится какой-либо путь из х0 в хn с положительной пропускной способностью. Просматривается первая строка и столбцы, содержащие элементы , помечается цифрой 0. При этом окажутся выделенными первые дуги возможных путей из х0 в хn. Далее просматриваются те строки, номера которых совпадают с номерами помеченных столбцов. В каждой такой iй строке отыскиваются элементы Cij > 0, находящиеся в непомеченных столбцах, и помечаются эти столбцы номером просматриваемой строки. Просмотр строк продолжается до тех пор, пока не будет помечен последний столбец.

3. В результате получаем первый путь из х0 в хп. Элементы этого пути Cij помечаем знаком минус, а симметричные элементы Cji – знаком плюс. Если просмотре таблицы столбец, соответствующий стоку, не будет помечен, то путь х0 в хп будет отсутствовать. 4. Определяется пропускная способность найденного пути, которая равна наименьшей из пропускных способностей дуг. 5. Определяются остаточные пропускные способности дуг найденного пути и симметричных ему дуг. Для этого из элементов вычитаем C 1, а к элементам прибавляем C 1. В результате получим новую таблицу с измененными пропускными способностями. 6. Процесс повторяем до тех пор, пока столбец хп не будет помечен. Больше не существует ни одного пути с положительной пропускной способностью из вершины x 0 в вершину xn.

7. На заключительном этапе вычитаем из элементов первой таблицы элементы последней таблица. Получаем проверочную таблицу. Положительные элементы этой таблицы характеризуют величины дуговых потоков. Величина максимального потока равна сумме элементов x 0 -й строки или сумме элементов хn-го столбца.

Пример 1. Найти максимальный поток транспортной сети Первый шаг: X 0 X 1(0) X 2(0) X 0 15– 17 X 1 0+ 9 X 2 0 9 X 3 0+ 0 X 4 4 X 5 X 3(1) X 4(2) X 5(3) 13– 16 4 10 8– 12 20 0+ 0 Путь l 1 = (x 0, х1, х3, х5, ). Пропускная способность

Второй шаг X 0 X 1 X 2 X 3 X 4 X 5 X 0 X 1(0) X 2(0) X 3(1) X 4(2) X 5(4) 8 0+ 7 9 8 17– 9 0 4+ 5 16 12 8 4– 10 0 20– 0+ l 2 = (x 0, х2, х4, х5) Третий шаг X 0 X 1 X 2 X 3 X 4 X 5 8+ 4 X 1(0) X 2(0) X 3(1) X 4(3) X 5(4) 7– 9 8+ 13 9 0 8 5– 16 0 10– 0 12+ 16– 8 4+ l 3 = (x 0, х1, х3, х4, х5). C 3 = min{7, 5, 10, 16} = 5

Четвертый шаг X 0 X 1(0) X 2(0) X 3(2) X 4(3) X 5(4) X 0 X 1 X 2 X 3 X 4 X 5 13 4+ 2 13– 9 0 9 16– 0 13 0+ 5– 0 8 17+ 11– 8 9+ l 4 = (x 0, х2, х3, х4, х5). C 4=min{13, 16, 5, 11} = 5. Пятый шаг. X 0 X 1(0) X 2(0) X 3(2) X 4 X 5 X 0 2 8 X 1 13 9 0 X 2 9 9 11 0 X 3 13 5 0 0 X 4 8 22 6 X 5 8 14 Просматривая строки и помечая столбцы, убеждаемся в том, что столбцы x 4 и x 5 пометить невозможно.

Следовательно, больше не существует ни одного пути с положительной пропускной способностью из вершины x 0 в вершину x 5. Подмножество R образуют помеченные вершины x 0, х1, х2, х3 , а подмножество – непомеченные вершины х4 и х 5. Разрез с минимальной пропускной способностью образуют дуги, начальные вершины которых принадлежат подмножеству R, а конечные – Удалив дуги этого разреза, блокируем все пути из источника в сток. Пропускная способность разреза

Заключительный шаг. X 0 X 1(0) X 2(0) X 3(1) X 4(2) X 5(3) X 0 X 1 X 2 X 3 X 4 X 5 0+ 0 15– 17 9 13– 9 16 4 0+ 0 10 4 12 0+ 0 X 0 X 1 X 2 X 3 X 4 X 5 8– 20 X 0 X 1(0) X 2(0) X 3(2) X 4 X 5 X 0 2 8 X 1 — 13 9 0 X 2 9 9 11 0 X 3 13 5 0 0 X 4 8 22 6 X 5 8 14 X 0 X 1(0) X 2(0) X 3(2) X 4 13 9 -13 0 13 -9 0 5 4 -13 -5 10 -4 -10 -8 -14 X 5 8 14

Положительные элементы проверочной характеризуют величины дуговых потоков. таблицы Величина максимального потока равна сумме элементов x 0 -й строки или сумме элементов х5 -го столбца.

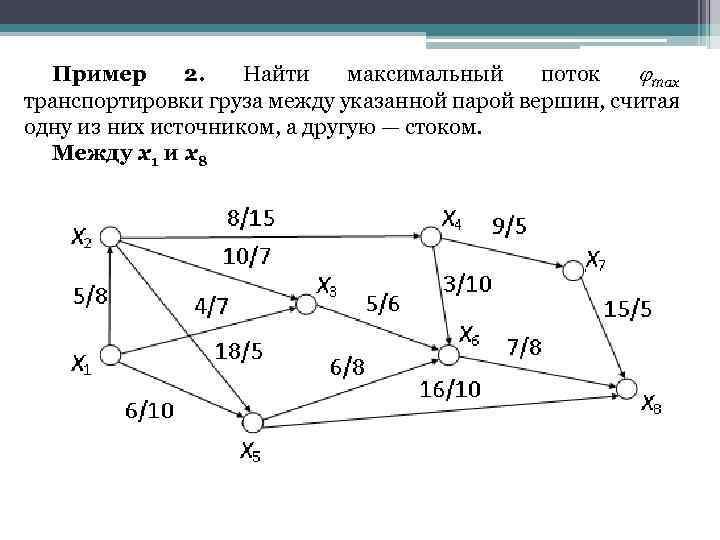Пример 2. Найти максимальный поток max транспортировки груза между указанной парой вершин, считая одну из них источником, а другую — стоком. Между x 1 и x 8

Первый шаг Второй шаг x 1 5 - 4 0 x 2 0+ 10 8 18 - x 3 0 0 5 3 9 x 4 0 3 9 6 0 0 167 15 x 5 6 0+ 6 10 - x 6 0 0 0 7 x 7 0 15 x 8 6+ 0 0 x 1 x 2 0 5 4 10 8 618 x 3 0 0 5 x 4 0 x 5 0+ 0 0 0 0 0+ x 6 x 7 x 8 x 2(1) x 3(1) x 4(2) x 5(1) x 6(3) x 7(4) x 8(5) l 1 = (x 1, х5, х8) x 2(1) x 3(1) x 4(2) x 5(2) x 6(3) x 7(4) x 8(5) l 2 = (x 1, х2, х5, х8)

Третий шаг. Четвертый шаг. x 1 x 2 x 3(1) x 4 x 5 x 6(3) x 7 x 8(6) x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 1 0 4 - 0 x 1 0 0 0 x 2 5 10 8 13 x 3 0+ 0 5 - x 3 4 0 1 x 4 0 3 9 x 5 6 5 x 6 0+ 0 0 7 - x 6 4 0 0 3 x 7 0 15 x 8 0 x 8 11 4 0 11 0+ l 3 = (x 1, х3, х6, х8). Подмножество R х1 х2, х3, х4, х5, х6, х7, х8

Удалив дуги этого разреза, блокируем все пути из источника в сток. Пропускная способность разреза Заключительный шаг. x 1 x 3 x 4 x 5 x 6 x 7 x 8 x 1 5 4 -5 0 -4 0 0 -6 -5 -4 0 0 6 5 0 4 0 0 11 4 x 7 0 0 x 8 -11 -4 0 x 2 x 3 x 4 x 5 x 6 x 2

3 Транспортная задача – это задача отыскания наиболее экономичного распределения потока по дугам транспортной сети. Решение транспортной задачи позволяет определить такое распределение маршрутов, которое обеспечивает минимальную стоимость перевозок или доставку грузов к потребителю в кратчайшее время. v. Транспортная задача по критерию стоимости v. Транспортная задача по критерию времени.

Транспортная задача по критерию стоимости Задана транспортная сеть, по которой должен быть пропущен поток φ, каждой дуге которой поставлены в соответствие две величины: Cij = С(хi, xj) – пропускная способность дуги (хi, xj); dij = d(хi, xj) – стоимость доставки единицы потока по дуге (хi, xj). Требуется найти такое распределение потока по дугам сети, которое обеспечивает минимальную стоимость прохождения потока.

Если рассматривать величины dij как длины соответствующих дуг, то задача минимизации стоимости прохождения потока φ по сети сведется к решению рассмотренной ранее задачи нахождения кратчайшего пути в графе от х0 до хn. При этом стоимость прохождения потока φ по найденному пути будет равна произведению длины этого пути на величину потока φ. Если нет ограничений на пропускную способность дуг, кратчайший путь является путем, который обеспечивает минимальную стоимость прохождения потока. При наличии ограничений на пропускные способности дуг нужно последовательно находить различные пути минимальной стоимости и пропускать потоки по ним до тех пор, пока суммарная величина потока по всем путям не будет равна заданной величине потока.

; ; ; . Для примера 2 стоимость доставки находиться следующим образом: Положительные элементы заключительной таблицы характеризуют величины дуговых потоков: Стоимость доставки груза определяется по формуле:

Алгоритм решения задачи при наличии ограничений на пропускные способности дуг: Первый шаг. В исходной сети S 1 с длинами дуг dij устанавливается кратчайший путь l 1 от х0 до хn. Второй шаг. Определяется пропускная способность пути l 1 С 1 = min Cij. По этому пути пропускается поток Если φ≤С 1 то задача решена и путь l 1 является наиболее экономичным для потока φ. Переходим к четвертому шагу. Если φ>С 1, то поток рассматривается как частичный и осуществляется переход к третьему шагу.

Третий шаг. Переходим к сети S 2, которая получается из S, путем замены пропускных способностей дуг Cij на Cij'. Дуги, у которых С = 0, исключаются из рассмотрения. Поток, распределение которого ищется в сети S 2, принимается равным Четвертый шаг. Стоимость перевозки транспортной сети определяется выражением грузов по

Транспортная задача по критерию времени. При решении транспортной задачи по критерию времени ребрам сети ставятся в соответствие величины tij, трактуемые как время, необходимое на перевозку груза из пункта хi в пункт x j. Очевидно, что время, необходимое на перевозку всех грузов из x 0 в хn, будет определяться путем, имеющим наибольшую продолжительность прохождения потока, так как перевозка грузов по остальным путям закончится раньше. Следовательно, время Т, необходимое на перевозку всех грузов, будет равно Для решения задачи нужно распределить весь поток φ таким образом, чтобы длительность наиболее продолжительного пути была бы минимальной.