Тема 5 Статистическое изучение связей Вопросы

Тема 5. Статистическое изучение связей

Вопросы • 1. Общая характеристика связей между явлениями и процессами • 2. Основные методы выявления наличия связи, ее характера и направления • 3. Линейный коэффициент корреляции 4. Методы корреляционно-регрессионного анализа • 5. Непараметрические показатели связи. Ранговые коэффициенты. • 6. Анализ зависимости между двумя альтернативными признаками. •

1. Общая характеристика связей между явлениями и процессами Задача статистики – обнаружить (выявить) зависимости как между количественными, так и между качественными показателями и дать им количественную характеристику.

Классификация признаков: • Факторные • Результативные

Виды связей: • функциональная • стохастическая

ФУНКЦИОНАЛЬНАЯ СВЯЗЬ • Определенному значению факторного признака соответствует одно и только одно значение результативного признака.

СТОХАСТИЧЕСКАЯ СВЯЗЬ • Причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений. • Связь можно обнаружить только при массовом наблюдении

Корреляционная связь • При корреляционной связи имеет место не изменение функции в зависимости от изменения аргумента, а имеет место вариация результативного признака вокруг его среднего значения в зависимости от изменения факторного признака.

Классификация корреляционных связей между явлениями и их признаками: • 1. По степени тесноты: практически отсутствует, слабая, умеренная, сильная • 2. По направлению: прямая, обратная • 3. По аналитическому выражению: прямолинейные ( линейные) и нелинейные. • 4. По количеству признаков факторов: парная, множественная

Изучение корреляционных связей сводится к решению следующих задач: • 1) выявление наличия (отсутствия) корреляционной связи между изучаемыми признаками; • 2) измерение тесноты связи между двумя (и более) признаками с помощью специальных коэффициентов (корреляционный анализ); • 3) определение уравнения регрессии – математической модели, в которой среднее значение результативного признака «у» рассматривается как функция одной или нескольких переменных – факторных признаков (регрессионный анализ).

2. Основные методы выявления наличия корреляционной связи, ее характера и направления • • метод сопоставления параллельных рядов, коэффициент корреляции знаков (Фехнера), графический, метод аналитических группировок, методы дисперсионного анализа, линейный коэффициент корреляции методы корреляционно- регрессионного анализа.

Метод сопоставления параллельных рядов • Приводится ряд данных по одному признаку и параллельно с ним по другому признаку, связь с которым предполагается. По вариации признака в первом и втором ряду судят о наличии связи признаков. Такой метод позволяет вывести только направление связи, но не измерить ее.

ПРИМЕР • Предположим, нужно выяснить, есть ли зависимость между объемом производства на предприятии и себестоимостью. Берем предприятия и ранжируем их по объему выпуска (по возрастанию), и смотрим, возрастает или уменьшается при этом себестоимость.

Коэффициент корреляции знаков (Фехнера) • Основан на сравнении поведения отклонений индивидуальных значений каждого признака (x и y) от своей средней величины. Во внимание принимаются не величины отклонений ( ) и ( ), а их знаки ( «+» или «–» ). • Определив знаки отклонений от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений (С) и несовпадений (Н). • Коэффициент Фехнера рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме, т. е. к общему числу наблюдаемых единиц: • Показатель тесноты связи, коэффициент Фехнера, может принимать значения от 0 до 1

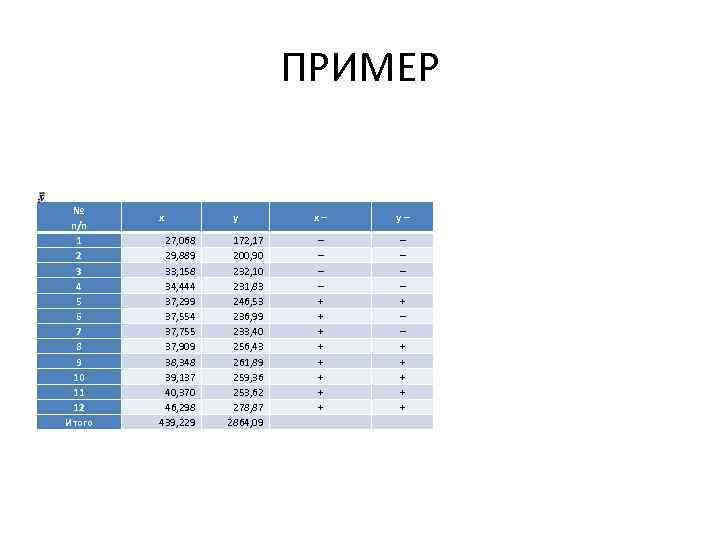ПРИМЕР № п/п 1 2 3 4 5 6 7 8 9 10 11 12 Итого x 27, 068 29, 889 33, 158 34, 444 37, 299 37, 554 37, 755 37, 909 38, 348 39, 137 40, 370 46, 298 439, 229 y 172, 17 200, 90 232, 10 231, 83 246, 53 236, 99 233, 40 256, 43 261, 89 259, 36 253, 62 278, 87 2864, 09 x– y– – – + + + + – – + + +

ПРИМЕР • Средние значения факторного и результативного признаков определяем по формуле средней арифметической простой : • В двух последних столбцах таблицы приведены знаки отклонений каждого х и у от своей средней величины. Число совпадений знаков – 10, а несовпадений – 2, тогда коэффициент корреляции знаков (Фехнера): КФ= 0, 667

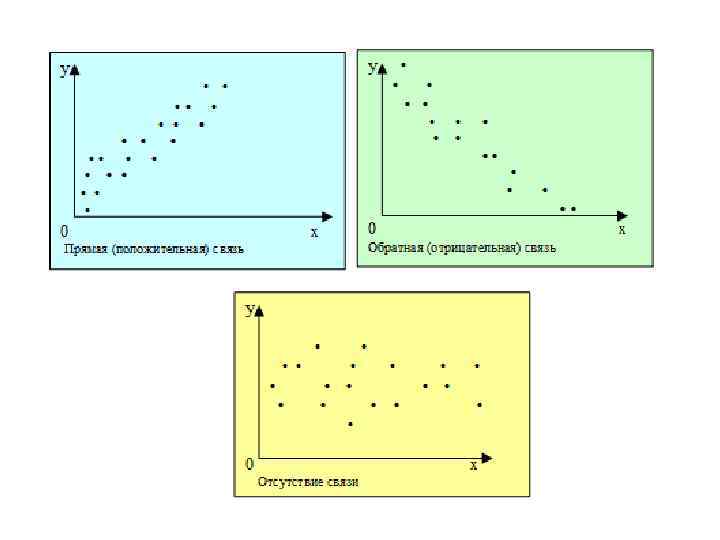
Графический метод • Графически взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат - результативного. Каждое пересечение линий, проводимых через эти оси, обозначаются точкой. По форме рассеяния точек на корреляционном поле судят о форме и тесноте связи.

Аналитическая группировка Сначала выбираются два признака: факторный и результативный. По факторному признаку производится группировка, а по результативному – подсчет средних или относительных величин. Путем сопоставления характера изменений значений факторного и результативного признака можно сделать вывод о наличии связи и ее направлении.

3. Линейный коэффициент корреляции

Измерение тесноты связи ►Для измерения тесноты прямолинейной связи между двумя признаками используется линейный коэффициент корреляции, который обозначается rxy ►Он может быть парным и множественным 21

Множественная корреляция ►Множественная корреляция занимается изучением, измерении связи между результативным признаком, двумя и более факторными. 22

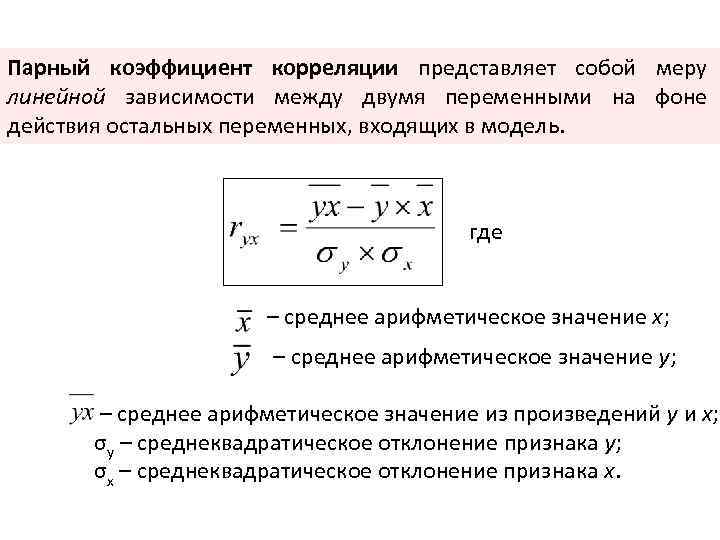Парный коэффициент корреляции представляет собой меру линейной зависимости между двумя переменными на фоне действия остальных переменных, входящих в модель. где – среднее арифметическое значение х; – среднее арифметическое значение у; – среднее арифметическое значение из произведений у и х; σу – среднеквадратическое отклонение признака у; σх – среднеквадратическое отклонение признака х.

Парный коэффициент корреляции изменяется в пределах от -1 до +1. Абсолютное значение, равное единице, свидетельствует о том, что связь функциональная: -1 – обратная (отрицательная), +1 – прямая (положительная). Нулевое значение коэффициента указывает на отсутствие линейной связи между признаками.

Пределы изменения парного коэффициента корреляции или 25

Проверка коэффициента корреляции на значимость (существенность). • Коэффициент корреляции рассчитывается для ограниченного числа наблюдений и подвержен случайным колебаниям, как и сами значения x и y, на основе которых он рассчитан, т. е. он содержит случайную ошибку и не всегда однозначно отражает действительно реальную связь между изучаемыми показателями. • Для оценки существенности (значимости) самого r рассчитывают среднюю квадратическую ошибку коэффициента корреляции σr. • Оценка существенности (значимости) r основана на сопоставлении значения r с его средней квадратической ошибкой:

4. Методы корреляционно- регрессионного анализа Общий термин «корреляционнорегрессионный анализ» подразумевает всестороннее исследование корреляционных связей (т. е. решение всех трех задач).

Этапы корреляционно-регрессионного анализа: 1) предварительный анализ объекта исследования; 2) сбор и первичная обработка информации; 3) построение уравнения регрессии и определение его параметров; 4) проверка адекватности полученной модели. 28

►По аналитическому выражению уравнение регрессии может быть линейным и нелинейным (криволинейным). ►Линейное уравнение регрессии характеризуется тем, что величина явления изменяется приблизительно равномерно в соответствии с изменением величины влияющего фактора. 29

Построение парного линейного уравнения Если имеется только один факторный признак, строится парная регрессия, выражающаяся уравнением прямой: Коэффициент регрессии а 1 показывает, на какую величину в среднем изменится результативный признак Y, если переменную Х увеличить на единицу ее собственного измерения. Свободный член уравнения а 0 характеризует усредненное влияние неучтенных в модели факторов (определяет начальные условия развития).

Параметры уравнения получают путем решения следующей системы нормальных уравнений: Рассчитанные по этому уравнению значения называются теоретическими (выравненными) значениями у.

Нелинейная регрессия Наиболее привлекательными с точки зрения простоты построения и экономической интерпретации являются линейные регрессионные модели. К ним прибегают всегда, в том числе и в случаях нелинейных связей, когда нет угрозы значительных потерь в точности оценок. Однако для некоторых зависимостей их представление в линейной форме приводит к ложным выводам. Тогда используют нелинейные регрессионные функции.

Параболическое уравнение парной регрессии Равноускоренное изменение результативного признака у при равномерном изменении фактора х говорит о параболической связи между признаками. При этом в некоторой точке связь может поменять свое направление: прямая связь перейти в обратную и наоборот. При парной параболической зависимости уравнение регрессии имеет вид: Параметры уравнения находят из следующей системы нормальных уравнений:

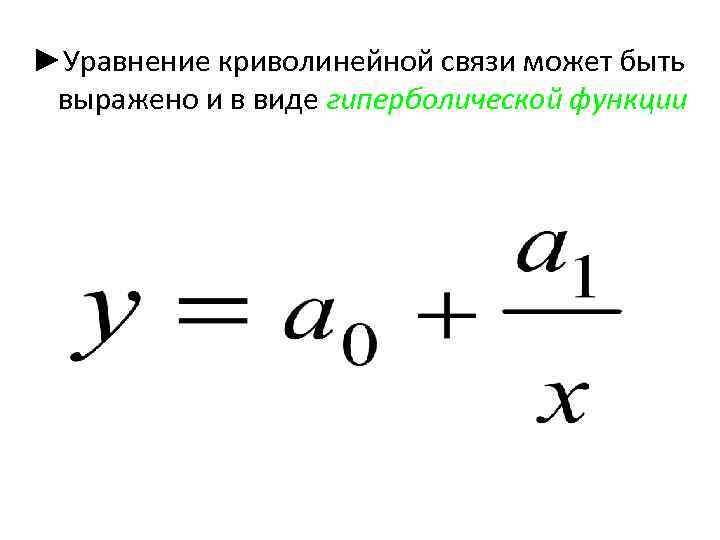►Уравнение криволинейной связи может быть выражено и в виде гиперболической функции 34

Для оценки параметров гиперболы в случае парной зависимости используется следующая система нормальных уравнений:

5. Непараметрические показатели связи. Ранговые коэффициенты. В анализе социально-экономических явлений часто приходится прибегать к различным условным оценкам с помощью рангов, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи.

Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы: 1) Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию). 2) Определить разности рангов каждой пары сопоставляемых значений. 3) Возвести в квадрат каждую разность и суммировать полученные результаты. 4) Вычислить коэффициент корреляции рангов по формуле: .

Коэффициент ранговой корреляции Спирмена - сумма квадратов разностей рангов, - число парных наблюдений

При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента равные: 0, 3 и менее, показателями слабой тесноты связи; значения более 0, 4, но менее 0, 7 - показателями умеренной тесноты связи, а значения 0, 7 и более показателями высокой тесноты связи.

6. Анализ зависимости между двумя альтернативными признаками. Теснота связи между 2 – мя альтернативными признаками может быть измерена с помощью 2 х коэффициентов: ассоциации и контингенции.

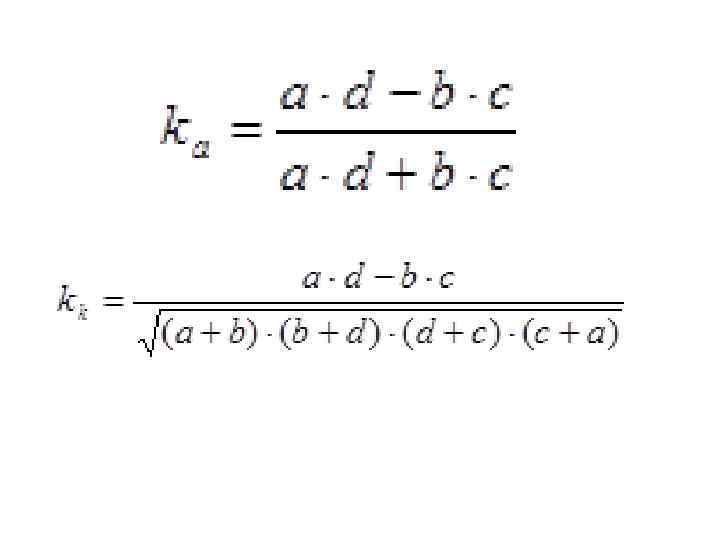
Коэффициент ассоциации и контингенции Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т. е. состоящим из двух качественно отличных от друга значений признака

Таблица для вычисления коэффициентов ассоциации и контингенции a b a+b c d c +d a+c b+d a+b+c+d