 Тема 5. Система МТ. Центр масс
Тема 5. Система МТ. Центр масс
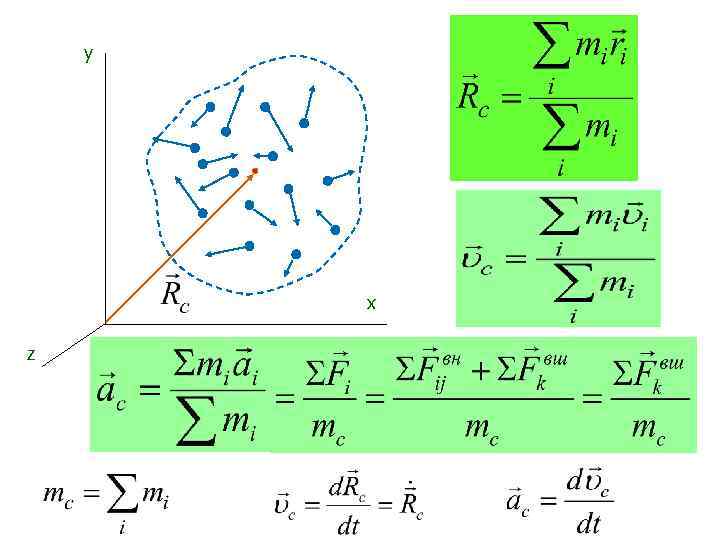 y x z
y x z
 Закон движения центра масс центр масс движется так же, как материальная точка с массой, равной полной массе системы, под действием всех внешних сил, приложенных к системе (к различным ее точкам).
Закон движения центра масс центр масс движется так же, как материальная точка с массой, равной полной массе системы, под действием всех внешних сил, приложенных к системе (к различным ее точкам).
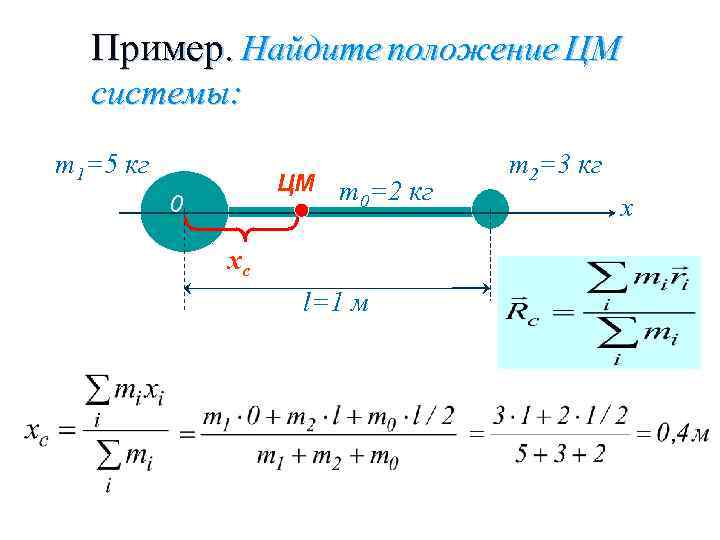 Пример. Найдите положение ЦМ системы: m 1=5 кг ЦМ 0 m 0=2 кг хс l=1 м m 2=3 кг х
Пример. Найдите положение ЦМ системы: m 1=5 кг ЦМ 0 m 0=2 кг хс l=1 м m 2=3 кг х
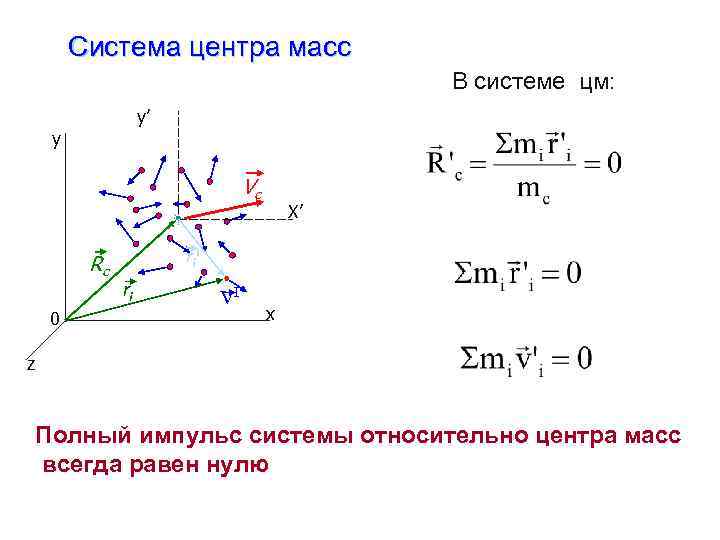 Система центра масс В системе цм: y’ y Vc ri Rc ri 0 X’ VI x z Полный импульс системы относительно центра масс всегда равен нулю
Система центра масс В системе цм: y’ y Vc ri Rc ri 0 X’ VI x z Полный импульс системы относительно центра масс всегда равен нулю
 Тема 6. Динамика вращательного движения
Тема 6. Динамика вращательного движения
 § 6. 1. Момент силы и момент импульса частицы Момент силы – мера механического воздействия на тело, приводящего во вращение (тело закреплено в одной точке - центре вращения).
§ 6. 1. Момент силы и момент импульса частицы Момент силы – мера механического воздействия на тело, приводящего во вращение (тело закреплено в одной точке - центре вращения).
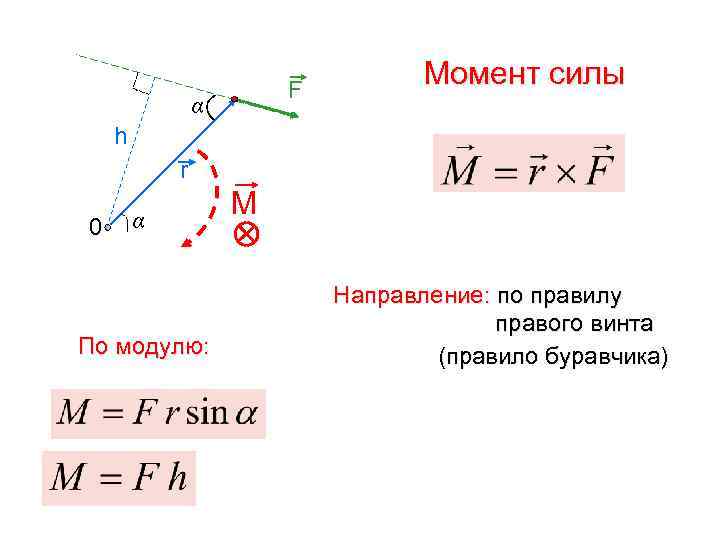 F α Момент силы h r 0 α По модулю: М Направление: по правилу правого винта (правило буравчика)
F α Момент силы h r 0 α По модулю: М Направление: по правилу правого винта (правило буравчика)
 Суммарный момент сил
Суммарный момент сил
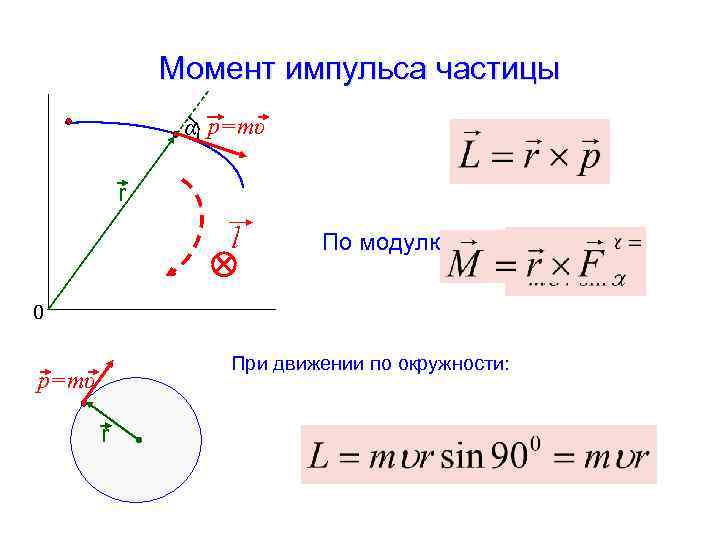 Момент импульса частицы α p=mυ r l По модулю: 0 При движении по окружности: p=mυ r
Момент импульса частицы α p=mυ r l По модулю: 0 При движении по окружности: p=mυ r
 Мера количества движения 1) Импульс МТ- мера количества поступательного движения тела 2) Момент импульса – мера количества движения при вращении
Мера количества движения 1) Импульс МТ- мера количества поступательного движения тела 2) Момент импульса – мера количества движения при вращении
 6. 2. Основной закон динамики вращения в общем виде (аналог 2 закона Ньютона для вращения ) 0 • Скорость изменения момента импульса СМТ равна равнодействующему моменту всех сил, приложенных к системе МТ:
6. 2. Основной закон динамики вращения в общем виде (аналог 2 закона Ньютона для вращения ) 0 • Скорость изменения момента импульса СМТ равна равнодействующему моменту всех сил, приложенных к системе МТ:
 Основной закон динамики (2 закон Ньютона в общем виде) 1) Поступательное движение Ø Скорость изменения импульса СМТ равна равнодействующей всех сил, приложенных к системе МТ: 2) Вращательное движение • Скорость изменения момента импульса СМТ равна равнодействующему моменту всех сил, приложенных к системе МТ:
Основной закон динамики (2 закон Ньютона в общем виде) 1) Поступательное движение Ø Скорость изменения импульса СМТ равна равнодействующей всех сил, приложенных к системе МТ: 2) Вращательное движение • Скорость изменения момента импульса СМТ равна равнодействующему моменту всех сил, приложенных к системе МТ:
 6. 3. Cохранение момента импульса частицы L = const, если Мр= 0 1) F = 0 (свободная частица) 2) Вектора r u F сонаправлены (сила центральная) 3) Cила F приложена к оси вращения (r=0)
6. 3. Cохранение момента импульса частицы L = const, если Мр= 0 1) F = 0 (свободная частица) 2) Вектора r u F сонаправлены (сила центральная) 3) Cила F приложена к оси вращения (r=0)
 6. 4. Закон сохранения момента импульса CМТ 1) В замкнутой системе (Мр=0); 2)В открытой, если Мр/д=0; 3)В проекции на направление, перпендикулярное Мр/д: если Мx=0, то ΔLx=0; 4)При кратковременных взаимодействиях: M ∙Δt=ΔL, Если Δt→ 0, то ΔL → 0.
6. 4. Закон сохранения момента импульса CМТ 1) В замкнутой системе (Мр=0); 2)В открытой, если Мр/д=0; 3)В проекции на направление, перпендикулярное Мр/д: если Мx=0, то ΔLx=0; 4)При кратковременных взаимодействиях: M ∙Δt=ΔL, Если Δt→ 0, то ΔL → 0.
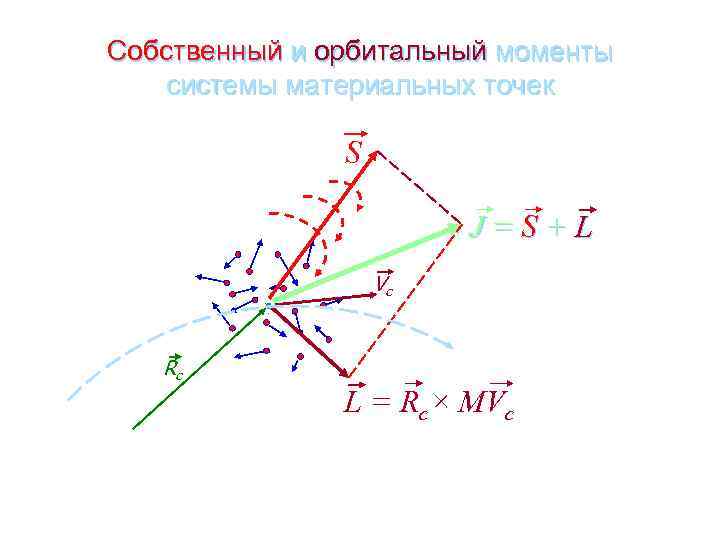 Собственный и орбитальный моменты системы материальных точек S J=S+L Vc Rc L = Rc× MVc
Собственный и орбитальный моменты системы материальных точек S J=S+L Vc Rc L = Rc× MVc
 Сохранение момента импульса
Сохранение момента импульса
 Связь полного момента импульса с собственным моментом импульса системы МТ S 0 0 C V Rc L
Связь полного момента импульса с собственным моментом импульса системы МТ S 0 0 C V Rc L
 Тема 6. Момент импульса частицы 6. 4. Собственный момент системы частиц
Тема 6. Момент импульса частицы 6. 4. Собственный момент системы частиц
 На примере двух частиц В системе центра масс (центр масс покоится): p 1 + p 2 = 0, S = l 1 + l 2 p 1 = - p 2 S 2. 1. p 1 p 2 C r 2 r 1 l 1 p 1 r 1 l 2 C r 2 p 2 l=r×p l 1 = 0, l 2 = 0 S=0 S = r 1×p 2 +r 1×p 2
На примере двух частиц В системе центра масс (центр масс покоится): p 1 + p 2 = 0, S = l 1 + l 2 p 1 = - p 2 S 2. 1. p 1 p 2 C r 2 r 1 l 1 p 1 r 1 l 2 C r 2 p 2 l=r×p l 1 = 0, l 2 = 0 S=0 S = r 1×p 2 +r 1×p 2