Тема 5 Представление информации в



































Информатика и ИКТ_лекции_5_6_2003_копия_новая.ppt
- Количество слайдов: 37
 Тема 5 Представление информации в компьютере 1
Тема 5 Представление информации в компьютере 1
 Архитектура ЭВМ – описание устройства и функционирования ЭВМ без подробностей технической реализации. В понятие архитектуры входит: описание основных функциональных узлов их информационного взаимодействия; описание способов представления информации в компьютере; описание структуры процессора и языка машинных команд. 2
Архитектура ЭВМ – описание устройства и функционирования ЭВМ без подробностей технической реализации. В понятие архитектуры входит: описание основных функциональных узлов их информационного взаимодействия; описание способов представления информации в компьютере; описание структуры процессора и языка машинных команд. 2
 Архитектура ЭВМ • Машина Неймана – архитектура ЭВМ, предложенная американским ученым Джоном фон Нейманом в 1946 году. Основные принципы включают: • Состав устройств однопроцессорной ЭВМ; • Использование двоичной СС в машинной арифметике; • Адресуемость памяти ЭВМ; • Хранение данных и программ в общей памяти ЭВМ; • Состав системы команд процессора. Принципы архитектуры Неймана во многом сохраняются в современных компьютерах 3
Архитектура ЭВМ • Машина Неймана – архитектура ЭВМ, предложенная американским ученым Джоном фон Нейманом в 1946 году. Основные принципы включают: • Состав устройств однопроцессорной ЭВМ; • Использование двоичной СС в машинной арифметике; • Адресуемость памяти ЭВМ; • Хранение данных и программ в общей памяти ЭВМ; • Состав системы команд процессора. Принципы архитектуры Неймана во многом сохраняются в современных компьютерах 3
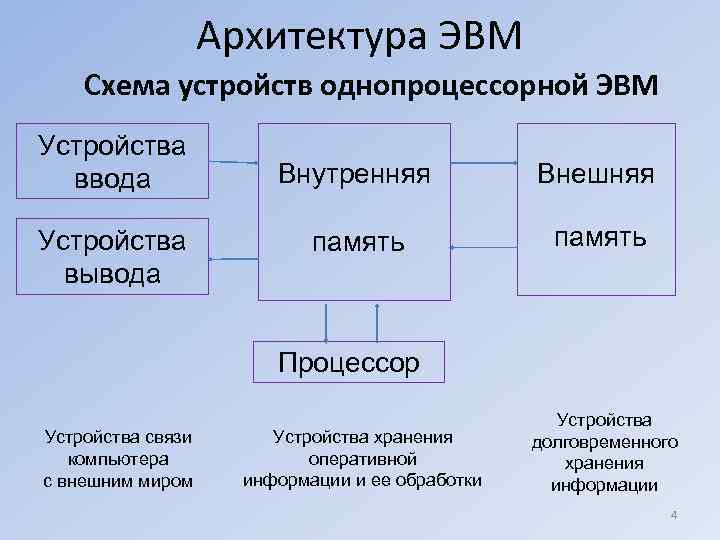
 Архитектура ЭВМ Схема устройств однопроцессорной ЭВМ Устройства ввода Внутренняя Внешняя Устройства память вывода Процессор Устройства связи Устройства хранения долговременного компьютера оперативной хранения с внешним миром информации и ее обработки информации 4
Архитектура ЭВМ Схема устройств однопроцессорной ЭВМ Устройства ввода Внутренняя Внешняя Устройства память вывода Процессор Устройства связи Устройства хранения долговременного компьютера оперативной хранения с внешним миром информации и ее обработки информации 4
 Формат машинной команды • Машинная программа – последовательность машинных команд • Принцип хранимой программы (принцип Неймана) – во время использования программа хранится в оперативной памяти вместе с данными. Каждая команда программы занимает ячейку памяти и имеет свой адрес (адрес ячейки). • Формат команды. Для всякого процессора машинная команда имеет стандартный формат и строго фиксирован- ную длину. Команда состоит из кода операции и адресной части. Код операции определяет действие, которое должен выполнить процессор; адресная часть содержит адреса величин, над которыми должна быть произведена операция • В зависимости от структуры адресной части команды процессоры делятся на трехадресные, двухадресные, одноадресные и 5 безадресные (стековые)
Формат машинной команды • Машинная программа – последовательность машинных команд • Принцип хранимой программы (принцип Неймана) – во время использования программа хранится в оперативной памяти вместе с данными. Каждая команда программы занимает ячейку памяти и имеет свой адрес (адрес ячейки). • Формат команды. Для всякого процессора машинная команда имеет стандартный формат и строго фиксирован- ную длину. Команда состоит из кода операции и адресной части. Код операции определяет действие, которое должен выполнить процессор; адресная часть содержит адреса величин, над которыми должна быть произведена операция • В зависимости от структуры адресной части команды процессоры делятся на трехадресные, двухадресные, одноадресные и 5 безадресные (стековые)
 Формат команды команда Код операции Адреса величин Что делать? Откуда взять или куда поместить? Пример формата трехадресной команды: А+В=С Код Адрес операции первого второго результата операнда Длина команды (d) N – количество команд процессора, k - оптимальная длина кода операции: 2 k-1 < N ≤ 2 k d = k + n*a, где k – длина поля кода операции, n – количество адресов в адресной части, a – длина поля адресной части 6
Формат команды команда Код операции Адреса величин Что делать? Откуда взять или куда поместить? Пример формата трехадресной команды: А+В=С Код Адрес операции первого второго результата операнда Длина команды (d) N – количество команд процессора, k - оптимальная длина кода операции: 2 k-1 < N ≤ 2 k d = k + n*a, где k – длина поля кода операции, n – количество адресов в адресной части, a – длина поля адресной части 6
 Двоичное кодирование информации в компьютере В компьютере для представления информации используется двоичное кодирование, так как удалось создать надежно работающие технические устройства, которые могут со стопроцентной надежностью сохранять и распознавать не более двух различных состояний (цифр): • электромагнитные реле • участок поверхности магнитного носителя информации • участок поверхности лазерного диска • триггер (используются в оперативной памяти компьютера 7
Двоичное кодирование информации в компьютере В компьютере для представления информации используется двоичное кодирование, так как удалось создать надежно работающие технические устройства, которые могут со стопроцентной надежностью сохранять и распознавать не более двух различных состояний (цифр): • электромагнитные реле • участок поверхности магнитного носителя информации • участок поверхности лазерного диска • триггер (используются в оперативной памяти компьютера 7
 Двоичное кодирование информации Все виды информации в компьютере кодируются на машинном языке, в виде логических последовательностей нулей и единиц Вид информации Двоичный код Числовая Текстовая Графическая 1 0 0 1 0 1 1 0 Звуковая Видео Информация в компьютере представлена в двоичном коде, алфавит которого состоит из двух цифр (0 и 1). Цифры двоичного кода можно рассматривать как два равновероят- ных состояния (события). При записи двоичной цифры реализуется выбор одного из двух возможных состояний (одной из двух цифр), т. е. несет количество информации 1 бит. (Название единицы измерения количества информации бит (bit) – от BInary digi. T – двоичная цифра). Каждая цифра машинного двоичного кода несет количество информации, равное 1 биту. Количество информации 8 в битах равно количеству цифр двоичного машинного кода.
Двоичное кодирование информации Все виды информации в компьютере кодируются на машинном языке, в виде логических последовательностей нулей и единиц Вид информации Двоичный код Числовая Текстовая Графическая 1 0 0 1 0 1 1 0 Звуковая Видео Информация в компьютере представлена в двоичном коде, алфавит которого состоит из двух цифр (0 и 1). Цифры двоичного кода можно рассматривать как два равновероят- ных состояния (события). При записи двоичной цифры реализуется выбор одного из двух возможных состояний (одной из двух цифр), т. е. несет количество информации 1 бит. (Название единицы измерения количества информации бит (bit) – от BInary digi. T – двоичная цифра). Каждая цифра машинного двоичного кода несет количество информации, равное 1 биту. Количество информации 8 в битах равно количеству цифр двоичного машинного кода.
 Представление информации в компьютере Структура внутренней памяти • Основные структурные единицы памяти компьютера: бит, байт, машинное слово. • Бит. Все данные и программы, хранящиеся в памяти компьютера, имеют вид двоичного кода. Один символ из двухсимвольного алфавита несет 1 бит информации. Ячейка памяти, хранящая один двоичный знак, называется «бит» . В одном бите памяти хранится один бит информации. Битовая структура памяти определяет первое свойство памяти – дискретность. 9
Представление информации в компьютере Структура внутренней памяти • Основные структурные единицы памяти компьютера: бит, байт, машинное слово. • Бит. Все данные и программы, хранящиеся в памяти компьютера, имеют вид двоичного кода. Один символ из двухсимвольного алфавита несет 1 бит информации. Ячейка памяти, хранящая один двоичный знак, называется «бит» . В одном бите памяти хранится один бит информации. Битовая структура памяти определяет первое свойство памяти – дискретность. 9
 Структура внутренней памяти • Байт. Восемь расположенных подряд битов памяти образуют байт. В одном байте памяти хранится один байт информации. Во внутренней памяти компьютера все байты пронумерованы. Нумерация начинается от нуля. Порядковый номер байта называется его адресом. В компьютере адреса обозначаются двоичным кодом. Используется также шестнадцатеричная форма обозначения адреса. • ПРИМЕР: Компьютер имеет оперативную память 2 Кбайт. Указать адрес последнего байта оперативной памяти (двоичный, восьмеричный, шестнадцатеричный). • Решение: Объем оперативной памяти составляет 2048 байт. Десятичный адрес (номер) последнего байта 2047, т. к. нумерация байтов памяти начинается с нуля. 204710 = 7 FF 16 = 0111 11112. 10
Структура внутренней памяти • Байт. Восемь расположенных подряд битов памяти образуют байт. В одном байте памяти хранится один байт информации. Во внутренней памяти компьютера все байты пронумерованы. Нумерация начинается от нуля. Порядковый номер байта называется его адресом. В компьютере адреса обозначаются двоичным кодом. Используется также шестнадцатеричная форма обозначения адреса. • ПРИМЕР: Компьютер имеет оперативную память 2 Кбайт. Указать адрес последнего байта оперативной памяти (двоичный, восьмеричный, шестнадцатеричный). • Решение: Объем оперативной памяти составляет 2048 байт. Десятичный адрес (номер) последнего байта 2047, т. к. нумерация байтов памяти начинается с нуля. 204710 = 7 FF 16 = 0111 11112. 10
 Структура внутренней памяти • Машинное слово. Последовательность битов, которую процессор может обрабатывать как единое целое, называют машинным словом. Длина машинного слова – 8, 16, 32 бита и т. д. (Это зависит от типа компьютера. ) • С другой стороны, машинное слово можно рассматривать как последовательность смежных в памяти байтов. Так, машинное слово из 16 битов состоит из 2 байтов. • Адрес машинного слова равен адресу младшего байта, входящих в это слово. Занесение информации в память и извлечение ее из памяти производится по адресам. Это свойство памяти называется адресуемостью. • ПРИМЕР: Объем ОП компьютера 1 Мбайт, адрес последнего машин-ного слова – 1 048 574. Чему равен размер машинного слова? • Решение: 1 Мбайт = 1024 Кбайт = 1 048 576 байт. Т. е. адрес 11 последнего байта 1 048 575. Значит последнее м. с. включает 2
Структура внутренней памяти • Машинное слово. Последовательность битов, которую процессор может обрабатывать как единое целое, называют машинным словом. Длина машинного слова – 8, 16, 32 бита и т. д. (Это зависит от типа компьютера. ) • С другой стороны, машинное слово можно рассматривать как последовательность смежных в памяти байтов. Так, машинное слово из 16 битов состоит из 2 байтов. • Адрес машинного слова равен адресу младшего байта, входящих в это слово. Занесение информации в память и извлечение ее из памяти производится по адресам. Это свойство памяти называется адресуемостью. • ПРИМЕР: Объем ОП компьютера 1 Мбайт, адрес последнего машин-ного слова – 1 048 574. Чему равен размер машинного слова? • Решение: 1 Мбайт = 1024 Кбайт = 1 048 576 байт. Т. е. адрес 11 последнего байта 1 048 575. Значит последнее м. с. включает 2
 Задача 1. Оперативная память компьютера содержит 163 840 машинных слов, что составляет 0, 625 Мбайт. Сколько битов содержит каждое машинное слово? Задача 2. Компьютер имеет объем оперативной памяти 0, 5 Кбайт. Адреса машинных слов меняются с шагом 4. Сколько машинных слов составляют оперативную память компьютера? Задача 3. Какой объем имеет оперативная память компьютера, если FF - шестнадцатеричный адрес последнего байта оперативной памяти? Задача 4. FЕ - шестнадцатеричный адрес последнего машинного слова оперативной памяти компьютера, объем которой составляет ¼ Кбайт. Найти длину машинного слова (в байтах). Задача 5. Какой объем имеет оперативная память компьютера, если 1 FЕ - шестнадцатеричный адрес последнего 2 -байтового машинного слова оперативной памяти? Задача 6. Компьютер имеет объем оперативной памяти 0, 5 Кбайт и содержит 128 машинных слов. Укажите адрес последнего байта и адрес последнего машинного слова памяти компьютера (в шестнадцатеричной форме). 12
Задача 1. Оперативная память компьютера содержит 163 840 машинных слов, что составляет 0, 625 Мбайт. Сколько битов содержит каждое машинное слово? Задача 2. Компьютер имеет объем оперативной памяти 0, 5 Кбайт. Адреса машинных слов меняются с шагом 4. Сколько машинных слов составляют оперативную память компьютера? Задача 3. Какой объем имеет оперативная память компьютера, если FF - шестнадцатеричный адрес последнего байта оперативной памяти? Задача 4. FЕ - шестнадцатеричный адрес последнего машинного слова оперативной памяти компьютера, объем которой составляет ¼ Кбайт. Найти длину машинного слова (в байтах). Задача 5. Какой объем имеет оперативная память компьютера, если 1 FЕ - шестнадцатеричный адрес последнего 2 -байтового машинного слова оперативной памяти? Задача 6. Компьютер имеет объем оперативной памяти 0, 5 Кбайт и содержит 128 машинных слов. Укажите адрес последнего байта и адрес последнего машинного слова памяти компьютера (в шестнадцатеричной форме). 12
 Структура дисков; файлы и каталоги Внешняя память компьютера используется длительного хранения информации. Устройства внешней памяти: магнитные диски и ленты, оптические (лазерные) диски, магнитооптические диски. Дисководы – устройства чтения/записи информации на диски Структура магнитного диска: одна или несколько сторон (магнитных поверхностей), разделенных на концентрические дорожки, каждая из которых поделена на секторы, состоящие из байтов. Все секторы на одном диске имеют фиксированный размер. Чтение/запись производится только полными секторами. Полный объем памяти диска: ОБЪЕМ = СТОРОНЫ*ДОРОЖКИ*СЕКТОРЫ*БАЙТЫ 13
Структура дисков; файлы и каталоги Внешняя память компьютера используется длительного хранения информации. Устройства внешней памяти: магнитные диски и ленты, оптические (лазерные) диски, магнитооптические диски. Дисководы – устройства чтения/записи информации на диски Структура магнитного диска: одна или несколько сторон (магнитных поверхностей), разделенных на концентрические дорожки, каждая из которых поделена на секторы, состоящие из байтов. Все секторы на одном диске имеют фиксированный размер. Чтение/запись производится только полными секторами. Полный объем памяти диска: ОБЪЕМ = СТОРОНЫ*ДОРОЖКИ*СЕКТОРЫ*БАЙТЫ 13
 Структура дисков; файлы и каталоги Информация на устройствах внешней памяти имеет файловую организацию. Файл – поименованная совокупность данных, хранящихся на внешнем носителе. Файловая структура диска - совокупность файлов на диске и взаимосвязей между ними. Логический диск – это физический диск или часть физического диска, которому присвоено собственное имя. Каталог – поименованная совокупность файлов и подкаталогов Путь к файлу – последовательность, состоящая из имен подкаталогов, начиная от корневого. Полное имя файла – состоит из имени логического диска, пути к файлу и имени файла. Дерево – графическое изображение иерархической файловой 14
Структура дисков; файлы и каталоги Информация на устройствах внешней памяти имеет файловую организацию. Файл – поименованная совокупность данных, хранящихся на внешнем носителе. Файловая структура диска - совокупность файлов на диске и взаимосвязей между ними. Логический диск – это физический диск или часть физического диска, которому присвоено собственное имя. Каталог – поименованная совокупность файлов и подкаталогов Путь к файлу – последовательность, состоящая из имен подкаталогов, начиная от корневого. Полное имя файла – состоит из имени логического диска, пути к файлу и имени файла. Дерево – графическое изображение иерархической файловой 14
 Задача 1. Двусторонняя дискета имеет объем 1200 Кбайт. Сколько дорожек на одной стороне дискеты, если каждая дорожка содержит 15 секторов по 4096 битов? Задача 2. Сколько файлов размером 100 Кбайт каждый можно разместить на дискете объемом 1) 1, 2 Мбайт; 2) 1, 44 Мбайт ? Задача 3. В результате повреждения односторонней дискеты 10 % секторов оказались дефектными, что составило 36 864 байта. Какой объем имеет дискета? Задача 4. Текст, записанный с помощью 16 -символьного алфавита, занимает 10 полных секторов на односторонней дискете объемом 180 Кбайт. Дискета разбита на 40 дорожек по 9 секторов. Сколько символов содержит текст? Задача 5. Пример 1 на странице 131 (учебник-практикум). 15
Задача 1. Двусторонняя дискета имеет объем 1200 Кбайт. Сколько дорожек на одной стороне дискеты, если каждая дорожка содержит 15 секторов по 4096 битов? Задача 2. Сколько файлов размером 100 Кбайт каждый можно разместить на дискете объемом 1) 1, 2 Мбайт; 2) 1, 44 Мбайт ? Задача 3. В результате повреждения односторонней дискеты 10 % секторов оказались дефектными, что составило 36 864 байта. Какой объем имеет дискета? Задача 4. Текст, записанный с помощью 16 -символьного алфавита, занимает 10 полных секторов на односторонней дискете объемом 180 Кбайт. Дискета разбита на 40 дорожек по 9 секторов. Сколько символов содержит текст? Задача 5. Пример 1 на странице 131 (учебник-практикум). 15
 Домашнее задание Задача 1. Объем оперативной памяти компьютера составляет 1/8 часть Мбайта. Сколько машинных слов составляют оперативную память, если одно машинное слово содержит 64 бита? Задача 2. Компьютер имеет объем оперативной памяти 1 Кбайт. Адреса машинных слов меняются с шагом 2. Сколько машинных слов составляют оперативную память компьютера? Задача 3. Какой объем имеет оперативная память компьютера, если FС - шестнадцатеричный адрес последнего 4 -байтового машинного слова оперативной памяти? Задача 4. Компьютер имеет объем оперативной памяти 1 Кбайт и содержит 512 машинных слов. Укажите адрес последнего байта и адрес последнего машинного слова памяти компьютера (в шестнадцатеричной форме). Задача 5. Какой объем имеет двусторонняя дискета, если каждая ее сторона разбита на 80 дорожек по 20 секторов на дорожке? Объем каждого сектора составляет 0, 5 Кбайт. 16
Домашнее задание Задача 1. Объем оперативной памяти компьютера составляет 1/8 часть Мбайта. Сколько машинных слов составляют оперативную память, если одно машинное слово содержит 64 бита? Задача 2. Компьютер имеет объем оперативной памяти 1 Кбайт. Адреса машинных слов меняются с шагом 2. Сколько машинных слов составляют оперативную память компьютера? Задача 3. Какой объем имеет оперативная память компьютера, если FС - шестнадцатеричный адрес последнего 4 -байтового машинного слова оперативной памяти? Задача 4. Компьютер имеет объем оперативной памяти 1 Кбайт и содержит 512 машинных слов. Укажите адрес последнего байта и адрес последнего машинного слова памяти компьютера (в шестнадцатеричной форме). Задача 5. Какой объем имеет двусторонняя дискета, если каждая ее сторона разбита на 80 дорожек по 20 секторов на дорожке? Объем каждого сектора составляет 0, 5 Кбайт. 16
 Тема 6 Представление символьной информации (двоичное кодирование текстовой информации) 17
Тема 6 Представление символьной информации (двоичное кодирование текстовой информации) 17
 Представление символьной информации Начиная с конца 60 -х годов ХХ века компьютеры все чаще стали использоваться для обработки текстовой информации. Для представления текстовой (символьной) информации в компьютере используется алфавит мощностью 256 символов. 256 = 28, т. е. один символ несет 8 бит (1 байт) информации. И двоичный код каждого символа в компьютером тексте занимает 1 байт памяти. Пример 1: сколько битов памяти компьютера займет слово «микропроцессор» ? Решение: Слово состоит из 14 букв, каждая буква является символом компьютерного алфавита, т. е. занимает 1 байт памяти. Значит все слово займет 14 байт = 112 битов памяти. 18
Представление символьной информации Начиная с конца 60 -х годов ХХ века компьютеры все чаще стали использоваться для обработки текстовой информации. Для представления текстовой (символьной) информации в компьютере используется алфавит мощностью 256 символов. 256 = 28, т. е. один символ несет 8 бит (1 байт) информации. И двоичный код каждого символа в компьютером тексте занимает 1 байт памяти. Пример 1: сколько битов памяти компьютера займет слово «микропроцессор» ? Решение: Слово состоит из 14 букв, каждая буква является символом компьютерного алфавита, т. е. занимает 1 байт памяти. Значит все слово займет 14 байт = 112 битов памяти. 18
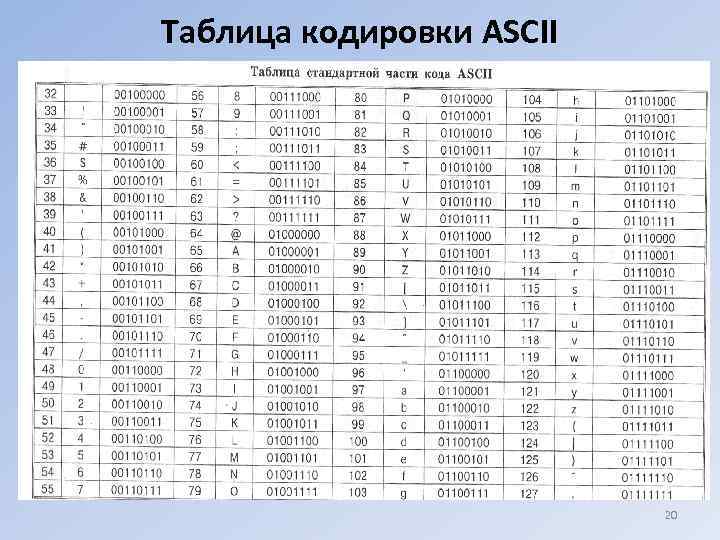
 Представление символьной информации • Таблица кодировки – таблица, в которой устанавливается соответствие между символами и их номерами (кодами) в компьютерном алфавите. • Кодирование заключается в том, что каждому символу компьютерного алфавита ставится в соответствие уникальный десятичный код от 0 до 255 или соответству- ющий ему 8 -разрядный двоичный код от 0000 до 1111. (Т. е. человек различает символы по начертанию, а компьютер – по их кодам. При вводе информации в компьютер происходит кодирование, при выводе - декодирование) • Для компьютеров типа IBM PC международным стандартом стала таблица кодировки ASCII (American Standard Code for Information Interchange) – Американский стандартный код для информационного обмена. 19
Представление символьной информации • Таблица кодировки – таблица, в которой устанавливается соответствие между символами и их номерами (кодами) в компьютерном алфавите. • Кодирование заключается в том, что каждому символу компьютерного алфавита ставится в соответствие уникальный десятичный код от 0 до 255 или соответству- ющий ему 8 -разрядный двоичный код от 0000 до 1111. (Т. е. человек различает символы по начертанию, а компьютер – по их кодам. При вводе информации в компьютер происходит кодирование, при выводе - декодирование) • Для компьютеров типа IBM PC международным стандартом стала таблица кодировки ASCII (American Standard Code for Information Interchange) – Американский стандартный код для информационного обмена. 19
 Таблица кодировки ASCII 20
Таблица кодировки ASCII 20
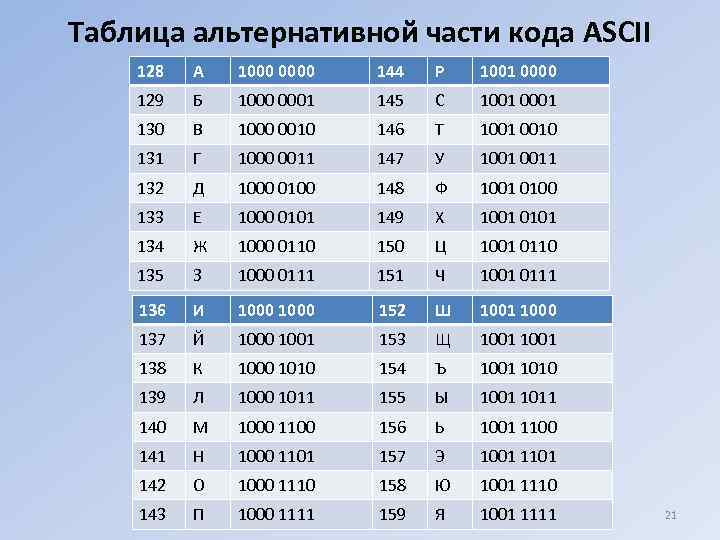
 Таблица альтернативной части кода ASCII 128 А 1000 0000 144 Р 1001 0000 129 Б 1000 0001 145 С 1001 0001 130 В 1000 0010 146 Т 1001 0010 131 Г 1000 0011 147 У 1001 0011 132 Д 1000 0100 148 Ф 1001 0100 133 Е 1000 0101 149 Х 1001 0101 134 Ж 1000 0110 150 Ц 1001 0110 135 З 1000 0111 151 Ч 1001 0111 136 И 1000 152 Ш 1001 1000 137 Й 1000 1001 153 Щ 1001 138 К 1000 1010 154 Ъ 1001 1010 139 Л 1000 1011 155 Ы 1001 1011 140 М 1000 1100 156 Ь 1001 1100 141 Н 1000 1101 157 Э 1001 1101 142 О 1000 1110 158 Ю 1001 1110 143 П 1000 1111 159 Я 1001 1111 21
Таблица альтернативной части кода ASCII 128 А 1000 0000 144 Р 1001 0000 129 Б 1000 0001 145 С 1001 0001 130 В 1000 0010 146 Т 1001 0010 131 Г 1000 0011 147 У 1001 0011 132 Д 1000 0100 148 Ф 1001 0100 133 Е 1000 0101 149 Х 1001 0101 134 Ж 1000 0110 150 Ц 1001 0110 135 З 1000 0111 151 Ч 1001 0111 136 И 1000 152 Ш 1001 1000 137 Й 1000 1001 153 Щ 1001 138 К 1000 1010 154 Ъ 1001 1010 139 Л 1000 1011 155 Ы 1001 1011 140 М 1000 1100 156 Ь 1001 1100 141 Н 1000 1101 157 Э 1001 1101 142 О 1000 1110 158 Ю 1001 1110 143 П 1000 1111 159 Я 1001 1111 21
 таблица кодировки ASCII • Первые 128 символов , с номерами от 0 до 127 (от 0000 до 0111 1111) являются стандартными (интернациональными). Причем первые 33 кода даже не символы, а операции (перевод строки и др. ). Далее идут прописные и строчные буквы латинского алфавита, арабские цифры, скобки, знаки препинания и т. п. ) • Остальные 128 кодов, с номерами от 128 до 255 (от 0111 1111 до 1111) используются для кодирования букв национальных алфавитов, научных символов и символов псевдографики). Сегодня существуют пять кодовых таблиц для русских букв (КОИ 8, СР 1251, СР 866, Мас, ISO). • В настоящее время широкое распространение получил новый международный стандарт Unicode, который отводит на каждый символ 2 байта, поэтому с его помощью можно закодировать N = 216 = 65 536 разных символов. Эту кодировку 22 поддерживают платформы Microsoft Windows & Office (начиная с
таблица кодировки ASCII • Первые 128 символов , с номерами от 0 до 127 (от 0000 до 0111 1111) являются стандартными (интернациональными). Причем первые 33 кода даже не символы, а операции (перевод строки и др. ). Далее идут прописные и строчные буквы латинского алфавита, арабские цифры, скобки, знаки препинания и т. п. ) • Остальные 128 кодов, с номерами от 128 до 255 (от 0111 1111 до 1111) используются для кодирования букв национальных алфавитов, научных символов и символов псевдографики). Сегодня существуют пять кодовых таблиц для русских букв (КОИ 8, СР 1251, СР 866, Мас, ISO). • В настоящее время широкое распространение получил новый международный стандарт Unicode, который отводит на каждый символ 2 байта, поэтому с его помощью можно закодировать N = 216 = 65 536 разных символов. Эту кодировку 22 поддерживают платформы Microsoft Windows & Office (начиная с
 Принцип последовательного кодирования алфавита В кодовой таблице ASCII латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Цифры также расположены по возрастанию. Благодаря этому в машинном представлении для символьной информации сохраняется понятие «алфавитный порядок» . Пример 2: Буква «i» в таблице кодировки символов имеет десятичный код 105. Что зашифровано последователь- ностью 108 105 110 107? Решение: здесь можно обойтись без таблицы кодировки, достаточно учесть принцип последовательного кодирова- ния алфавита и вспомнить порядок букв: j – 106, k-107 … Ответ: это слово «link» 23
Принцип последовательного кодирования алфавита В кодовой таблице ASCII латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Цифры также расположены по возрастанию. Благодаря этому в машинном представлении для символьной информации сохраняется понятие «алфавитный порядок» . Пример 2: Буква «i» в таблице кодировки символов имеет десятичный код 105. Что зашифровано последователь- ностью 108 105 110 107? Решение: здесь можно обойтись без таблицы кодировки, достаточно учесть принцип последовательного кодирова- ния алфавита и вспомнить порядок букв: j – 106, k-107 … Ответ: это слово «link» 23
 Пример 3: С помощью последовательности десятичных кодов 99 111 109 112 117 116 101 114 зашифровано слово computer. Какая последовательность десятичных кодов будет соответствовать этому же слову, написан- ному заглавными буквами? Решение: здесь также можно обойтись без таблицы кодировки, достаточно учесть, что разница между десятичными кодами строчной и соответствующей прописной буквы равна 32. Т. е. «с» - 99, «С» – 67 и т. п. Ответ: «COMPUTER» - 67 79 77 80 85 84 69 82. 24
Пример 3: С помощью последовательности десятичных кодов 99 111 109 112 117 116 101 114 зашифровано слово computer. Какая последовательность десятичных кодов будет соответствовать этому же слову, написан- ному заглавными буквами? Решение: здесь также можно обойтись без таблицы кодировки, достаточно учесть, что разница между десятичными кодами строчной и соответствующей прописной буквы равна 32. Т. е. «с» - 99, «С» – 67 и т. п. Ответ: «COMPUTER» - 67 79 77 80 85 84 69 82. 24
 Текстовая информация, хранящаяся в памяти компью- тера в двоичном коде, неудобна для восприятия чело- веком из-за своей многозначности. На практике внутреннее представление чаще всего перекодируется в шестнадцатеричную форму. Шестнадцатеричный код каждого символа – двузначное число от 00 до FF. Пример 4: Последовательность двоичных кодов : 01110011 01110100 01101111 01110000 соответствует слову «stop» . Построить внутреннее шестнадцатеричное представление этого слова. Решение: заменяем каждые 4 двоичные цифры одной шестнадцатеричной. Ответ: 73 74 6 F 70. 25
Текстовая информация, хранящаяся в памяти компью- тера в двоичном коде, неудобна для восприятия чело- веком из-за своей многозначности. На практике внутреннее представление чаще всего перекодируется в шестнадцатеричную форму. Шестнадцатеричный код каждого символа – двузначное число от 00 до FF. Пример 4: Последовательность двоичных кодов : 01110011 01110100 01101111 01110000 соответствует слову «stop» . Построить внутреннее шестнадцатеричное представление этого слова. Решение: заменяем каждые 4 двоичные цифры одной шестнадцатеричной. Ответ: 73 74 6 F 70. 25
 Задача 1. Текст занимает 5 страниц, на каждой странице 30 строк по 70 символов в строке. Какой объем ОП (в байтах) занимает текст? Задача 2. Десятичный код латинской буквы «е» в таблице кодировки ASCII равен 101. Какая последовательность десятичных кодов будет соответствовать словам file и help ? Задача 3. Десятичный код латинской буквы «о» в таблице кодировки ASCII равен 111. Что зашифровано с помощью последовательности деся- тичных кодов 1)115 112 111 114 116 2) 109 111 117 115 101? Задача 4. Пользуясь таблицей кодировки символов ASCII, закодируйте с помощью двоичных и шестнадцатеричных кодов слова EXCEL, Word. Задача 5. По шестнадцатеричному коду восстановить двоичный код и, пользуясь таблицей кодировки, расшифровать 1) 42 61 73 69 63 26 2) 50 61 73 63 61 6 С.
Задача 1. Текст занимает 5 страниц, на каждой странице 30 строк по 70 символов в строке. Какой объем ОП (в байтах) занимает текст? Задача 2. Десятичный код латинской буквы «е» в таблице кодировки ASCII равен 101. Какая последовательность десятичных кодов будет соответствовать словам file и help ? Задача 3. Десятичный код латинской буквы «о» в таблице кодировки ASCII равен 111. Что зашифровано с помощью последовательности деся- тичных кодов 1)115 112 111 114 116 2) 109 111 117 115 101? Задача 4. Пользуясь таблицей кодировки символов ASCII, закодируйте с помощью двоичных и шестнадцатеричных кодов слова EXCEL, Word. Задача 5. По шестнадцатеричному коду восстановить двоичный код и, пользуясь таблицей кодировки, расшифровать 1) 42 61 73 69 63 26 2) 50 61 73 63 61 6 С.
 Домашнее задание Задача 1. Свободный объем оперативной памяти компьютера составляет 640 Кбайт. Сколько страниц книги поместится в ней, если на странице 32 строки по 64 символа в строке? Задача 2. Десятичный код латинской буквы «i» в таблице кодировки ASCII равен 105. Какая последовательность десятичных кодов будет соответствовать слову INFORMATION, записанному заглавными буквами? Задача 3. По 16 -ичному коду восстановить 2 -ичный код и, пользуясь таблицей кодировки, расшифровать 1)57 69 6 Е 64 6 F 77 73 2 D 39 35 2) 63 6 F 6 D 65 2 D 4 F 4 E 2 D 6 C 69 6 E 65. Задача 4. Пользуясь таблицей кодировки, получить шестнадцатеричный 27
Домашнее задание Задача 1. Свободный объем оперативной памяти компьютера составляет 640 Кбайт. Сколько страниц книги поместится в ней, если на странице 32 строки по 64 символа в строке? Задача 2. Десятичный код латинской буквы «i» в таблице кодировки ASCII равен 105. Какая последовательность десятичных кодов будет соответствовать слову INFORMATION, записанному заглавными буквами? Задача 3. По 16 -ичному коду восстановить 2 -ичный код и, пользуясь таблицей кодировки, расшифровать 1)57 69 6 Е 64 6 F 77 73 2 D 39 35 2) 63 6 F 6 D 65 2 D 4 F 4 E 2 D 6 C 69 6 E 65. Задача 4. Пользуясь таблицей кодировки, получить шестнадцатеричный 27
 Тема 7 Представление числовой информации (представление целых чисел) 28
Тема 7 Представление числовой информации (представление целых чисел) 28
 Представление чисел в памяти ПК Для представления чисел в памяти компьютера используются два формата: • формат с фиксированной точкой (запятой), • Формат с плавающей точкой (запятой). В формате с фиксированной точкой представ- ляются только целые числа, в формате с плавающей точкой – вещественные числа (целые, дробные и смешанные). 29
Представление чисел в памяти ПК Для представления чисел в памяти компьютера используются два формата: • формат с фиксированной точкой (запятой), • Формат с плавающей точкой (запятой). В формате с фиксированной точкой представ- ляются только целые числа, в формате с плавающей точкой – вещественные числа (целые, дробные и смешанные). 29
 Представление целых чисел • Целые числа в компьютере хранятся в формате с фиксированной точкой (запятой). В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а «точка» «находится» справа после младшего разряда, т. е. вне разрядной сетки. • Множество целых чисел, представляемых в памяти компьютера, ограничено. Диапазон значений зависит от размера ячеек памяти, используемых для их хранения. • В k-разрядной ячейке может храниться 2 k различных целых чисел. Причем если числа только неотрицатель- ные, то диапазон их значений 0 … 2 k – 1, если числа положительные и отрицательные ( «числа со 30 знаком» ), то диапазон их значений – 2 k – 1 … 2 k – 1.
Представление целых чисел • Целые числа в компьютере хранятся в формате с фиксированной точкой (запятой). В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а «точка» «находится» справа после младшего разряда, т. е. вне разрядной сетки. • Множество целых чисел, представляемых в памяти компьютера, ограничено. Диапазон значений зависит от размера ячеек памяти, используемых для их хранения. • В k-разрядной ячейке может храниться 2 k различных целых чисел. Причем если числа только неотрицатель- ные, то диапазон их значений 0 … 2 k – 1, если числа положительные и отрицательные ( «числа со 30 знаком» ), то диапазон их значений – 2 k – 1 … 2 k – 1.
 Представление целых чисел 1. Ячейка памяти 1 байт (k = 8 бит). Тип чисел – короткое целое. Диапазон чисел а) неотрицательных: 0 … 255 (0 … 28– 1) б) положительных и отрицательных: – 128 … 127 (– 27 … 27– 1). 2. Ячейка памяти 2 байта (k = 16 бит). Тип чисел – целое. Диапазон чисел а) неотрицательных: 0 … 65 535 (0… 216 – 1) б) положительных и отрицательных: – 32 768 … 32 767 (– 215 … 215 – 1). 3. Ячейка памяти 4 байта (k = 32 бита). Тип чисел – длинное целое. Диапазон чисел а) неотрицательных: 0 … 4 294 967 296 (0… 232 – 1) б) положительных и отрицательных: – 2 147 483 648 … 2 147 483 647 (– 231 … 231 – 1). 31
Представление целых чисел 1. Ячейка памяти 1 байт (k = 8 бит). Тип чисел – короткое целое. Диапазон чисел а) неотрицательных: 0 … 255 (0 … 28– 1) б) положительных и отрицательных: – 128 … 127 (– 27 … 27– 1). 2. Ячейка памяти 2 байта (k = 16 бит). Тип чисел – целое. Диапазон чисел а) неотрицательных: 0 … 65 535 (0… 216 – 1) б) положительных и отрицательных: – 32 768 … 32 767 (– 215 … 215 – 1). 3. Ячейка памяти 4 байта (k = 32 бита). Тип чисел – длинное целое. Диапазон чисел а) неотрицательных: 0 … 4 294 967 296 (0… 232 – 1) б) положительных и отрицательных: – 2 147 483 648 … 2 147 483 647 (– 231 … 231 – 1). 31
 Представление положительных целых чисел • Обычно для хранения целых чисел со знаком отводится две ячейки памяти (16 битов), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый разряд записывается 0, если отрицательное, то 1. • Представление в компьютере положительных чисел с использованием формата «знак – величина» называется прямым кодом числа. • Пример: число 200210 = 111110100102 будет представлено в 16 -разрядном представлении следующим образом: 0 0 0 1 1 1 0 0 1 0 • Максимальное положительное число (с учетом выделения одного разряда на знак) для целых чисел со знаком в n-разрядном представлении равно А = 2 n-1 – 1. 32
Представление положительных целых чисел • Обычно для хранения целых чисел со знаком отводится две ячейки памяти (16 битов), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый разряд записывается 0, если отрицательное, то 1. • Представление в компьютере положительных чисел с использованием формата «знак – величина» называется прямым кодом числа. • Пример: число 200210 = 111110100102 будет представлено в 16 -разрядном представлении следующим образом: 0 0 0 1 1 1 0 0 1 0 • Максимальное положительное число (с учетом выделения одного разряда на знак) для целых чисел со знаком в n-разрядном представлении равно А = 2 n-1 – 1. 32
 Алгоритм получения внутреннего представления целого положительного числа N, хранящегося в k-разрядном машинном слове 1. Перевести число N в двоичную систему счисления. 2. Полученный результат дополнить слева незначащими нулями до k разрядов. 3. При необходимости получить шестнадцатеричную форму внутреннего представления числа, заменяя каждые четыре 2 -чных символа одной 16 -ичной цифрой. Пример1: получить внутреннее представление целого числа 1607 в 2 -байтовой ячейке. Решение: N = 160710 = 110010001112. Внутреннее представление этого числа 0000 0110 0100 0111. 16 -ичная форма внутреннего представления 0647. 33
Алгоритм получения внутреннего представления целого положительного числа N, хранящегося в k-разрядном машинном слове 1. Перевести число N в двоичную систему счисления. 2. Полученный результат дополнить слева незначащими нулями до k разрядов. 3. При необходимости получить шестнадцатеричную форму внутреннего представления числа, заменяя каждые четыре 2 -чных символа одной 16 -ичной цифрой. Пример1: получить внутреннее представление целого числа 1607 в 2 -байтовой ячейке. Решение: N = 160710 = 110010001112. Внутреннее представление этого числа 0000 0110 0100 0111. 16 -ичная форма внутреннего представления 0647. 33
 Представление отрицательных целых чисел • Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что упрощает работу процессора и увеличивает его быстродействие. • Дополнительный код отрицательного числа А, хранящегося в n ячейках, равен 2 n – |A|. Алгоритм получения внутреннего представления целого отрицательного числа (– N) в k-разрядном м. с. 1. Получить внутреннее представление положительного числа N (т. е. модуля данного числа) в прямом коде. 2. Получить обратный код этого числа, инвертировав все биты (т. е. все 1 заменить на 0, а все 0 заменить на 1). 3. К полученному числу прибавить 1. 4. При необходимости получить шестнадцатеричную 34 форму внутреннего представления числа.
Представление отрицательных целых чисел • Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что упрощает работу процессора и увеличивает его быстродействие. • Дополнительный код отрицательного числа А, хранящегося в n ячейках, равен 2 n – |A|. Алгоритм получения внутреннего представления целого отрицательного числа (– N) в k-разрядном м. с. 1. Получить внутреннее представление положительного числа N (т. е. модуля данного числа) в прямом коде. 2. Получить обратный код этого числа, инвертировав все биты (т. е. все 1 заменить на 0, а все 0 заменить на 1). 3. К полученному числу прибавить 1. 4. При необходимости получить шестнадцатеричную 34 форму внутреннего представления числа.
 Пример2: получить внутреннее представление целого отрицательного числа – 1607 в 2 -байтовой ячейке. Решение: 1. Внутреннее представление модуля числа: 0000 0110 0100 0111. 2. Обратный код: 1111 1001 1011 1000. 3. Результат прибавления 1: 1111 1001 1011 1001. 4. 16 -ичная форма внутреннего представления F 9 B 9. Алгоритм восстановления целого числа из внутреннего представления в k-разрядном машинном слове 1. Перевести число из 16 -ичной СС в 2 -ичную СС. 2. Проверить знаковый разряд: если 1, то число отрицательное и хранится в дополнительном коде. Необходимо вычесть 1, инвертировать число, и получим прямой код. Если знаковый разряд 0, то число положительное и уже хранится в прямом коде. 3. Перевести число из двоичной СС в десятичную СС. Пример: восстановить число из внутреннего представления F 67 D 35
Пример2: получить внутреннее представление целого отрицательного числа – 1607 в 2 -байтовой ячейке. Решение: 1. Внутреннее представление модуля числа: 0000 0110 0100 0111. 2. Обратный код: 1111 1001 1011 1000. 3. Результат прибавления 1: 1111 1001 1011 1001. 4. 16 -ичная форма внутреннего представления F 9 B 9. Алгоритм восстановления целого числа из внутреннего представления в k-разрядном машинном слове 1. Перевести число из 16 -ичной СС в 2 -ичную СС. 2. Проверить знаковый разряд: если 1, то число отрицательное и хранится в дополнительном коде. Необходимо вычесть 1, инвертировать число, и получим прямой код. Если знаковый разряд 0, то число положительное и уже хранится в прямом коде. 3. Перевести число из двоичной СС в десятичную СС. Пример: восстановить число из внутреннего представления F 67 D 35
 Достоинства и недостатка представления чисел в формате с фиксированной точкой (запятой) • + • Простота и наглядность представления чисел • Простота алгоритмов реализации арифметических операций • – • Небольшой диапазон представления величин, недостаточный для решения математических, физических и т. п. задач 36
Достоинства и недостатка представления чисел в формате с фиксированной точкой (запятой) • + • Простота и наглядность представления чисел • Простота алгоритмов реализации арифметических операций • – • Небольшой диапазон представления величин, недостаточный для решения математических, физических и т. п. задач 36
 Задача 1. Компьютер работает только с целыми положительными числами. Каков диапазон изменения чисел, если для представления числа в памяти компьютера отводится 1 байт? Задача 2. Каков диапазон изменения чисел (положительных и отрицательных), если для представления числа в памяти компьютера отводятся 4 байта? Задача 3. Диапазон изменения целых положительных и отрицательных чисел, которые можно разместить в машинном слове, составляет от – 215 до 215 -1. Сколько битов (байтов) размер машинного слова? Задача 4. Записать в 2 -ичной и 16 -ичной форме внутреннее представление наибольшего положительного целого и наибольшего по абсолютной величине отрицательного целого числа, представленного в 2 -байтовой ячейке памяти. Задача 5. Представители племени Мульти оперируют целыми положительными числами и умеют считать только до 100. Для проведения расчетов в племени применяется калькулятор. Указать минимальную длину ячейки памяти в битах, необходимую для хранения чисел. 37
Задача 1. Компьютер работает только с целыми положительными числами. Каков диапазон изменения чисел, если для представления числа в памяти компьютера отводится 1 байт? Задача 2. Каков диапазон изменения чисел (положительных и отрицательных), если для представления числа в памяти компьютера отводятся 4 байта? Задача 3. Диапазон изменения целых положительных и отрицательных чисел, которые можно разместить в машинном слове, составляет от – 215 до 215 -1. Сколько битов (байтов) размер машинного слова? Задача 4. Записать в 2 -ичной и 16 -ичной форме внутреннее представление наибольшего положительного целого и наибольшего по абсолютной величине отрицательного целого числа, представленного в 2 -байтовой ячейке памяти. Задача 5. Представители племени Мульти оперируют целыми положительными числами и умеют считать только до 100. Для проведения расчетов в племени применяется калькулятор. Указать минимальную длину ячейки памяти в битах, необходимую для хранения чисел. 37

