Тема 5 АЛГОРИТМИ СОРТУВАННЯ ПОРІВНЯЛЬНИЙ АНАЛІЗ

Тема 5 АЛГОРИТМИ СОРТУВАННЯ. ПОРІВНЯЛЬНИЙ АНАЛІЗ • • Не робіть за допомогою більшого те, що можна зробити за допомогою меншого. • (Д. Пойа) • 5. 1 Вступ • У словниках слово "сортування" (sorting) визначається як "розподіл, добір по сортах; розподіл на категорії, сорти, розряди", однак програмісти звичайно використовують це слово в більш вузькому змісті, позначаючи їм перегрупування елементів у деякому визначеному порядку. Цей процес, мабуть, варто було б назвати не сортуванням, а впорядкуванням (ordering) або ранживанням (sequencing). Однак слово сортування вже міцно ввійшло в програмістський "жаргон", тому ми будемо надалі використовувати слово "сортування" у вузькому змісті. Виходить, тепер можна сформулювати визначення "сортування", що буде використовуватися далі.

5. 1 Вступ • Сортування - це процес перегрупування заданої множини об'єктів у деякому визначеному порядку. Ціль сортування - полегшити пошук елементів. • Алгоритм сортування — це алгоритм для упорядкування елементів у списку. У випадку, коли елемент списку має кілька полів, поле, по якому виробляється сортування називається ключем сортування. На практиці як ключ часто виступає число, а в інших полях зберігаються які -небудь дані, що ніяк не впливають на роботу алгоритму. • Мабуть, ніяка інша проблема не породила такої кількості різнобарвних рішень, як задача сортування. Чи існує якийсь «універсальний» , найкращий алгоритм? Узагалі говорячи, немає. Однак, маючи приблизні характеристики вхідних даних, можна підібрати метод, що працює оптимальним образом. • Існує безліч методів сортування, кожний з яких має свої достоїнства і недоліки. Алгоритми сортування мають велике прикладне значення, вони цікаві і самі по собі. Ця, досить глибоко досліджена область інформатики, використовується в інформаційно-пошукових системах, у військовій і банківській справі.

5. 1 Вступ • Крім загальнонаукового інтересу до алгоритмів сортування, у кожнім алгоритмі цікаво оцінити і його так називану складність. Під складністю розуміється максимальне число елементарних кроків алгоритму. При рішенні задачі сортування масивів звичайно висувається вимога мінімального використання додаткової пам'яті, з якого випливає неприпустимість використання додаткових масивів. • Для оцінки швидкодії алгоритмів різних методів сортування, як правило, використовують два показники: • кількість присвоювань; • кількість порівнянь;

5. 1 Вступ • • Також важливими є такі показники, як: Пам'ять. Ряд алгоритмів вимагає виділення додаткової пам'яті під тимчасове збереження даних. Стійкість. Стійке сортування не змінює взаємного розташування рівних елементів. Така властивість може бути дуже корисним, якщо вони складаються з декількох полів, а сортування відбувається по одному з них. Природність поводження. Ефективність роботи методу при обробці уже відсортованих, або частково відсортованих даних. Алгоритм поводиться природно, якщо враховує цю характеристику вхідної послідовності і працює краще. Усі методи сортування можна розділити на дві великі групи: прямі методи сортування; поліпшені методи сортування; Поліпшені методи сортування ґрунтуються на тих же принципах, що і прямі, але використовують деякі оригінальні ідеї для прискорення методу сортування. Прямі методи сортування на практиці використовуються досить рідко, тому що мають відносно низьку швидкодію. Однак вони добре показують суть заснованих на них поліпшених методів. Крім того, у деяких випадках (як правило, при невеликій довжині масиву і/або особливому вихідному розташуванні елементів масиву) деякі з прямих методів можуть навіть перевершити поліпшені методи.

5. 2 Опис алгоритмів • • • Сортування простими вставками Наш перший алгоритм, алгоритм сортування методом вставок, призначений для рішення задачі сортування (sorting problem), сформульованої вище. Приведемо ще раз це формулювання. Вхід: послідовність з n чисел (a 1, а 2, …, аn). Вихід: перестановка (зміна порядку) вхідної послідовності таким чином, що для її членів виконується співвідношення.

5. 2 Опис алгоритмів

5. 2 Опис алгоритмів • Принцип роботи методу. • Масив розділяється на дві частини: відсортовану і не відсортовану. Елементи з несортованої частини по черзі вибираються і вставляються у відсортовану частину так, щоб не порушити в ній упорядкованість елементів. На початку роботи алгоритму як відсортовану частину масиву приймають тільки один перший елемент, а в якості не відсортованої частини – всі інші елементи. • Таким чином, алгоритм буде складатися з n-1 -го проходу (n – розмірність масиву), кожний з яких буде включати чотири дії: • узяття чергового i-го невідсортованого елемента і збереження його в додатковій змінній; • пошук позиції j у відсортованій частині масиву, у якій присутність узятого елемента не порушить упорядкованості елементів; • зрушення елементів масиву від i-1 -го до j-1 -го вправо, щоб звільнити знайдену позицію вставки; • вставка узятого елемента в знайдену j-ю позицію.

5. 2 Опис алгоритмів • Псевдокод сортування методом вставок представлений нижче за назвою Insertion_Sort. На його вхід подається масив А [1. . n], що містить послідовність з n чисел (кількість елементів масиву А позначено в цьому коді як length[A]. ) Вхідні числа сортуються без використання додаткової пам'яті: їхня перестановка виробляється в межах масиву, і обсяг використовуваної при цьому додатковій пам'яті не перевищує деяку постійну величину. По закінченні роботи алгоритму Insertion_Sort вхідний масив містить відсортовану послідовність: • Insertion_Sort(А) • 1 for j ← 2 to length[A] • 2 do key ← A[j] • 3 Вставка елемента A[j] у відсортовану послідовність A[1. . j-1] • 4 i ← j-l • while i > 0 і A[i] > key • 6 do A[i + 1] ← A[i] • 7 i ← i-1 • 8 A[i + 1] ← key

5. 2 Опис алгоритмів • • Сортування злиттям Багато корисних алгоритмів мають рекурсивну структуру: для рішення даної задачі вони рекурсивно викликають самі себе один або кілька разів, щоб вирішити допоміжну задачу, що має безпосереднє відношення до поставленої задачі. Такі алгоритми найчастіше розробляються за допомогою методу декомпозиції, або розбивки: складна задача розбивається на більш прості, котрі подібні вихідній задачі, але мають менший обсяг; далі ці допоміжні задачі вирішуються рекурсивним методом, після чого отримані рішення комбінуються з метою одержати рішення вихідної задачі. Парадигма, що лежить в основі методу декомпозиції "розділяй і пануй", на кожнім рівні рекурсії містить у собі три етапи. Поділ задачі на підзадачі. Скорення — рекурсивне рішення цих підзадач. Коли обсяг підзадачи досить малий, виділені підзадачи вирішуються безпосередньо. Комбінування рішення вихідної задачі з рішень допоміжних задач. Алгоритм сортування злиттям (merge sort) у великому ступені відповідає парадигмі методу розбивки. На інтуїтивному рівні його роботу можна описати в такий спосіб.

5. 2 • Поділ: послідовність, що складається з n елементів, розбивається на дві менші послідовності, кожна з яких містить n/2 елементів. • Скорення: сортування обох допоміжних послідовностей методом злиття. • Комбінування: злиття двох відсортованих послідовностей для одержання остаточного результату. • Рекурсія досягає своєї нижньої межі, коли довжина послідовності стає рівної 1. У цьому випадку вся робота вже зроблена, оскільки будь-яку таку послідовність можна вважати упорядкованої.

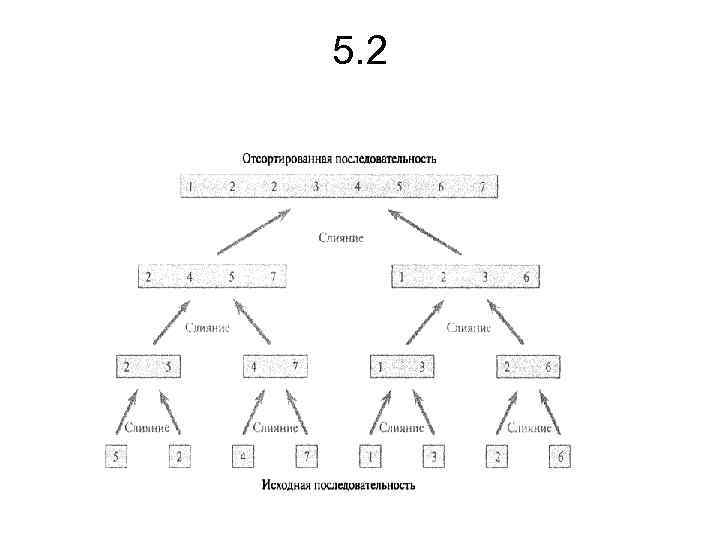
5. 2 • Основна операція, що виробляється в процесі сортування по методу злиття, — це об'єднання двох відсортованих послідовностей у ході комбінування (останній етап). Це робиться за допомогою допоміжної процедури MERGE(A, p, q, r), де А — масив, а р, q і r — індекси, що нумерують елементи масиву, такі, що р < q < r. У цій процедурі передбачається, що елементи підмасивів А[p, . . q] і A [q + 1, . r] упорядковані. Вона зливає ці два подмассива в один відсортований, елементи якого заміняють поточні елементи подмассива А[p, . . r]. • Принцип роботи методу. • Алгоритм Неймана упорядкування масиву (алгоритм сортування злиттями) заснований на багаторазових злиттях вже упорядкованих груп елементів масиву. Спочатку весь масив розглядається як сукупність упорядкованих груп по одному елементі в кожній. Злиттям сусідніх груп одержуємо упорядковані групи, кожна з яких містить два елементи (крім, можливо, останньої групи, який не найшлося парної). Далі, упорядковані групи укрупнюються тим же способом і т. д.

5. 2 • Алгоритм дає гарні показники по швидкості роботи, навіть у порівнянні із сортуванням методом бінарних дерев. Єдиний недолік - необхідність використовувати додатковий масив того ж розміру. • Процедура MERGE_SORT(A, p, г) виконує сортування елементів у подмассиве A[р. . r]. Якщо справедливо нерівність р r, то в цьому подмассиве утримується не більш одного елемента, і, таким чином, він відсортований. У противному випадку виробляється розбивка, у ході якого обчислюється індекс q, що розділяє масив A[р. . г] на два подмассива: A[p. . q] з елементами і A [q. . r] з елементами. • MERGE_SORT(A, p, r) • 1 if p < r • 2 then q←[(p+r)/2] • 3 MERGE_SORT(A, p, q) • 4 MERGE_SORT(A, q+1, r) • 5 MERGE(A, p, q, r)

5. 2 • • • • • Щоб відсортувати послідовність А = (А[1], А[2], . . . , А[п]), викликається процедура Merge_Sort(A, 1, length [А]), де length [А] = п. На мал. 5. 2 проілюстрована робота цієї процедури у висхідному напрямку, якщо п — це ступінь двійки. Тепер процедуру MERGE можна використовувати як підпрограму в алгоритмі сортування злиттям. MERGE(A, p, q, r) 1 n 1 ← q- p + 1 2 n 2 ← r - q 3 Створюємо масиви L[1. . n 1 + 1] і R[1. . n 2 + 1] 4 for i ← 1 to n 1 5 do L[i] ← A[p+ i -1] 6 for j ← 1 to n 2 7 do R[j] ← A[q +j] 8 L[n 1 + 1] ← ∞ 9 R[n 2 + 1] ← ∞ 10 i← 1 11 j← 1 12 for до k← p to r 13 do if L[i] <= R[j] 14 then A[k] ← L[i] 15 i←i+1 16 else A[k] ← R[j] 17 j←j+1

5. 2

5. 2 • 3 Пірамідальне сортування (сортування за допомогою купи) • Розглянемо ще один алгоритм сортування, а саме пірамідальне сортування. Час роботи цього алгоритму, як і час роботи алгоритму сортування злиттям (і на відміну від часу роботи алгоритму сортування вставкою), дорівнює O(nlgn). Як і сортування методом вставок, і на відміну від сортування злиттям, пірамідальне сортування виконується без залучення додаткової пам'яті: у будьякий момент часу потрібна пам'ять для збереження поза масивом тільки деякої постійної кількості елементів. Таким чином, у пірамідальному сортуванні сполучаться кращі особливості двох розглянутих раніше алгоритмів сортування.

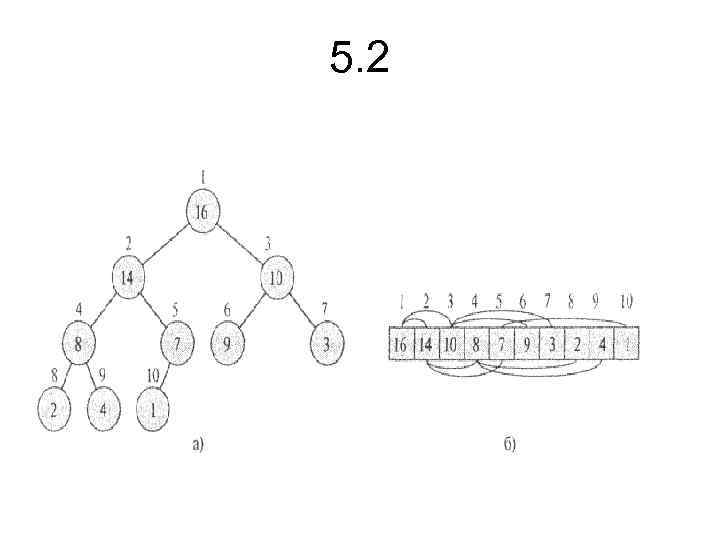
5. 2 • Піраміда (binary heap) - це структура даних, що представляє собою об'єкт-масив, якому можна розглядати як майже повне бінарне дерево (див. тему 2). Кожен вузол цього дерева відповідає визначеному елементові масиву. На всіх рівнях, крім, може бути, останнього, дерево цілком заповнене (заповнений рівень — це такий, котрий містить максимально можливу кількість вузлів). Останній рівень заповнюється ліворуч праворуч доти, поки в масиві не закінчаться елементи. Масив, що представляє піраміду, А є об'єктом із двома атрибутами:

5. 2

5. 2 • Принцип роботи методу. • Алгоритм заснований на тому, що сортуємому масивові може бути поставлене у відповідність двоїчне дерево, кожен вузол якого відповідає одному елементові масиву з деяким номером k і цей вузол містить посилання на два інших вузли, що відповідають елементам з номерами 2 k+1 і 2 k+2. Корінь дерева відповідає елементові з номером 0 (нуль). • Подальші дії наступні - масив переупорядковується так, щоб для будь-якого k виконувалися нерівності: • M[k]≥M[k+1], M[k]≥M[k+2], • Потім масив ще раз переупорядковується, уже по зростанню номерів. Кожний з цих кроків вимагає операцій. • Природно, такий алгоритм працює швидше і вимагає менше пам'яті, але, напевно, він ще менш очевидний, чим рекурсивний.

5. 2 • • • Heapsort(A) 1 Build_Max_Heap(A) 2 for i ←length[A] downto 2 3 do Обміняти A[1] ↔ A[i] 4 heap_size[A] ← hеар_size[A] - 1 5 Max_Heapify(A, 1)

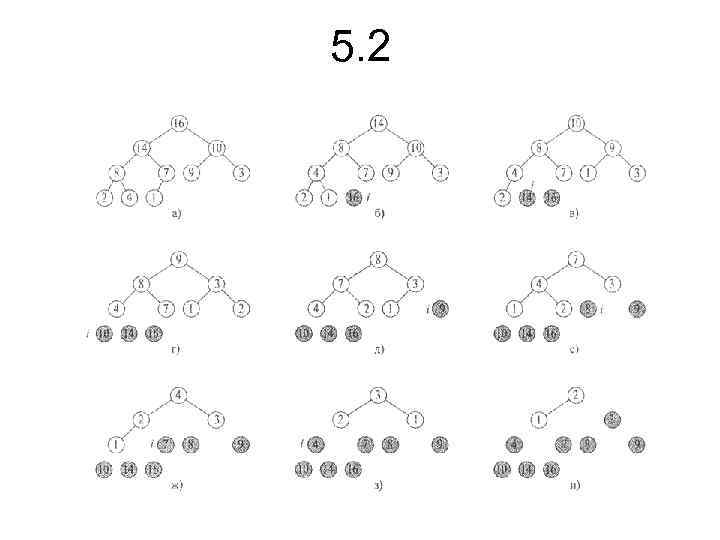
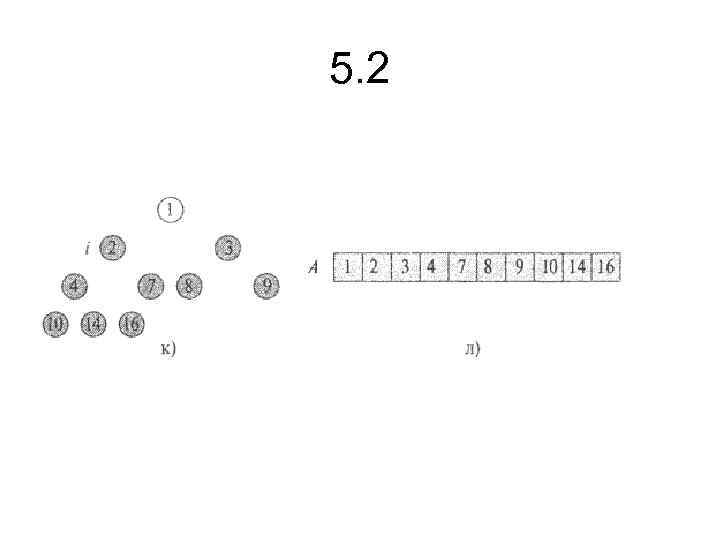
5. 2 • На мал. 5. 4 показаний приклад пірамідального сортування після попередньої побудови незростаючої піраміди. У кожній частині цього малюнка зображена незростаюча піраміда перед виконанням чергової ітерації циклу for у рядках 2 -5. У частині а) цього малюнка показана вихідна незростаюча піраміда, отримана за допомогою процедури BUILD_MAX_HEAP. У частинах б)-к) показані піраміди, що виходять у результаті виклику процедури MAX_HEAPIFY у рядку 5. У кожній з цих частин зазначене значення індексу i. У піраміді утримуються только вузли, зафарбовані ясносірим кольором. У частині л) показаний масив, що вийшов у кінцевому підсумку, А. • Час роботи процедури Heapsort дорівнює О (nlgn), оскільки виклик процедури Build_Max_Heap вимагає часу 0(п), а кожний з п — 1 викликів процедури Max_Heapify — часу О (lgn).

5. 2

5. 2

5. 2 • Приведемо псевдокоди процедур BUILD_MAX_HEAP (створення піраміди з неупорядкованого масиву даних) і MAX_HEAPIFY (підтримка властивостей піраміди). • Max_Heapify(A, i) • 1 l ←LEFT(i) • 2 r ← Rl. GHT(i) • 3 if l ≤heap_size[A] і А[l] > A[i] • 4 then largest ← l • 5 else largest ← i • 6 if r heap_size[A] і A[r] > A[largest] • 7 then largest ← r • 8 if largest ≠i • 9 then Обміняти A[i] ↔A[largest] 10 Max_Heapify(A, largest) • Build_Max_Heap(A) • 1 heap_size[A] ←length[A] • 2 for i [length[A]/2] downto 1 • 3 do MAX_HEAPIFY(A, i)

5. 2 • 4 Швидке сортування • Швидке сортування — це алгоритм сортування, час роботи якого для вхідного масиву з n чисел у найгіршому випадку дорівнює O (п 2). Незважаючи на таку повільну роботу в найгіршому випадку, цей алгоритм на практиці найчастіше виявляється оптимальним завдяки тому, що в середньому час його роботи набагато краще: O (n lgn). Алгоритм володіє також тим перевагою, що сортування в ньому виконується без використання додаткової пам'яті, тому він добре працює навіть у середовищах з віртуальною пам'яттю.

5. 2 • Принцип роботи методу. • Швидке сортування, подібно сортуванню злиттям, заснована на парадигмі "розділяй і пануй". Нижче описаний процес сортування підмасива А [p. . r], що складається, як і всі алгоритми з використанням декомпозиції, із трьох етапів. • Поділ. Масив А [p. . r] розбивається (шляхом переупорядкування його елементів) на два (можливо, порожніх) підмасива A [p. . q-1] і A[q+ 1. . r]. Кожен елемент підмасива • A [p. . q-1] не перевищує елемент A[q], а кожен елемент підмасива [q+ 1. . r] не менше елемента A[q]. Індекс q обчислюється в ході процедури розбивки. • Скорення. Підмасиви A [p. . q-1] і A[q+ 1. . r] сортуються шляхом рекурсивного виклику процедури швидкого сортування. • Комбінування. Оскільки підмасиви сортуються на місці, для їхнього об'єднання не потрібні ніякі дії: весь масив А [р. . г] виявляється відсортований.

5. 2 • • • • • Алгоритм сортування реалізується представленою нижче процедурою: Quicksort (A, p, r) 1 if р < r 2 then q ← Partition (A, p, r) 3 Quicksort (A, p, q- 1) 4 Quicksort (A, q + 1, r) Щоб виконати сортування всього масиву А, виклик процедури повинний мати вигляд Quicksort(A, 1, lehgth [A]). Ключовою частиною розглянутого алгоритму сортування є процедура PARTITION, що змінює порядок елементів подмассива А [p. . r] без залучення додаткової пам'яті: Partitionist(A, p, r ) 1 х ←А[r] 2 i ← р-1 3 for j ← р to r - 1 4 do if A[j] ≤x 5 then i ← i + 1 6 Обміняти А[i] ↔ A[j] 7 Обміняти A[i + 1] ↔ A [r] 8 return і + 1

5. 2 • Продуктивність швидкого сортування добре вивчена. Алгоритм піддавався математичному аналізові, тому існують точні математичні формули, що стосуються питань його продуктивності. Результати аналізу були неодноразово перевірені емпіричними шляхом і алгоритм був відпрацьований до такого стану, що став найбільш кращим для широкого спектра задач сортування. Схожі способи реалізації підходять також і для інших алгоритмів, але в алгоритмі швидкого сортування ми можемо використовувати них із упевненістю, оскільки його продуктивність добре вивчена.

5. 3 Теоретичні аспекти визначення часу виконання сортувань • Час роботи процедури l. NSERTION_SORT залежить від набору вхідних значень: для сортування тисячі чисел потрібно більше часу, чим для сортування трьох чисел. Крім того, час сортування за допомогою цієї процедури може бути різним для послідовностей, що складаються з того самого кількості елементів, у залежності від ступеня упорядкованості цих послідовностей до початку сортування. У загальному випадку час роботи алгоритму збільшується зі збільшенням кількості вхідних даних, тому загальноприйнята практика — представляти час роботи програми як функцію, що залежить від кількості вхідних елементів. Для цього поняття "час роботи алгоритму" і "розмір вхідних даних" потрібно визначити точніше

5. 2 • Найбільш адекватне поняття розміру вхідних даних (input size) залежить від розглянутої задачі. У багатьох задачах, таких, як сортування або дискретні перетворення Фур'є, ця кількість вхідних елементів, наприклад, розмір п масиву. Для багатьох інших задач, таких, як перемножування двох цілих чисел, найбільш підходяща міра для виміру розміру введення — загальна кількість бітів, необхідних для представлення вхідних даних у звичайних двоїчих позначеннях. Іноді розмір вводу зручніше описувати за допомогою не одного, а двох чисел. Наприклад, якщо на вхід алгоритму подається граф, розмір вводу можна описувати, указуючи кількість вершин і ребер графа. Для кожної розглянутої далі задачі буде вказуватися спосіб виміру розміру вхідних даних.

• Час роботи алгоритму для того або іншого вводу виміряється в кількості елементарних операцій, або "кроків", які необхідно виконати. Тут зручно ввести поняття кроку, щоб міркування були як можна більш машиннонезалежними. На даному етапі ми будемо виходити з точки зору, відповідно до якої для виконання кожного рядка псевдокоду потрібне фіксований час. Час виконання різних рядків може відрізнятися, але ми припустимо, що та сама i-я рядок виконується за час ci, де ci константа.

• У наступних міркуваннях формула для виразу часу роботи алгоритму Insertion_Sort, що спочатку буде складним образом залежати від усіх величин ci, значно спроститься завдяки більш лаконічним позначенням, з якими простіше працювати. Ці більш прості позначення дозволять легше визначити, який із двох алгоритмів ефективніше. • Почнемо з того, що введемо для процедури INSERTION_SORT час виконання кожної інструкції і кількість їхніх повторень. Для кожного j = 2, 3, . . . , n, де n = length [А], позначимо через tj кількість перевірок умови в циклі while (рядок 5). При нормальному завершенні циклів for або while (тобто коли перестає виконуватися умова, задане в заголовку циклу) умова перевіряється на один раз більше, ніж виконується тіло циклу. Саме собою зрозуміло, ми вважаємо, що коментарі не є інструкціями, що виконуються, тому вони не збільшують час роботи алгоритму: ci

INSERTION_SORT

INSERTION_SORT • Час роботи алгоритму — це сума проміжків часу, необхідних для виконання кожної вхідної в його склад інструкції, що виконується. Якщо виконання інструкції триває протягом часу ci і вона повторюється в алгоритмі п раз, то її внесок у повний час роботи алгоритму дорівнює ci n. Щоб обчислити час роботи алгоритму l. NSERTION_SORT (позначимо його через Т (n)), потрібно просуммировать добутку значень, що коштують у стовпцях час і кількість разів, у результаті чого одержимо • . (5. 1)

INSERTION_SORT • Навіть якщо розмір вхідних даних є фіксованою величиною, час роботи алгоритму може залежати від ступеня упорядкованості сортируемых величин, який вони володіли до введення. Наприклад, сама добра нагода для алгоритму INSERTION_Sort — це коли всі елементи масиву уже відсортовані. Тоді для кожного j = 2, 3, . . . , n виходить, що А[i] key у рядку 5, ще коли i дорівнює своєму початковому значенню j — 1. Таким чином, при j = = 2, 3, . . . , n tj = 1, і час роботи алгоритму в самій добрій нагоді обчислюється так: • T(n)=c 1 n+c 2(n-1)+c 4(n-1)+c 5(n-1)+c 8(n 1)=(c 1+c 2+c 4+c 5+c 8)n-(c 2+c 4+c 5+c 8). (5. 2) • Це час роботи можна записати як an + b, де а і b — константи, що залежать від величин ci ; тобто цей час є лінійною функцією від п.

• Якщо елементи масиву відсортовані в порядку, зворотному необхідному (у даному випадку в порядку убування), то це найгірший випадок. Кожен елемент A [j] необхідно порівнювати з всіма елементами уже відсортованої підмножини A [1. . j — 1] так, що для • j =2, 3, . . . , n значення tj = j. З обліком того, що

INSERTION_SORT • (як виконується це підсумовування, показано в додатку А), одержуємо, що час роботи алгоритму l. NSERTION-SORT у гіршому випадку визначається співвідношенням • (5. 3) • Це час роботи можна записати як an 2 + bn + з, де константи а, b і з залежать від сi. Таким чином, це квадратична функція від п.

INSERTION_SORT • Це час роботи можна записати як an 2 + bn + з, де константи а, b і з залежать від сi. Таким чином, це квадратична функція від п. • Аналізуючи алгоритм, що працює по методу вставок, ми розглядали як найкращий, так і найгірший випадок, коли елементи масиву були розсортовані в порядку, зворотному необхідному. Далі ми будемо приділяти основну увагу визначенню тільки часу роботи в найгіршому випадку, тобто максимальному часі роботи з усіх вхідних даних розміру п. Тому є три причини:

INSERTION_SORT • • • час роботи алгоритму в найгіршому випадку - це верхня межа цієї величини для будь-яких вхідних даних. Розташовуючи цим значенням, ми точно знаємо, що для виконання алгоритму не буде потрібно більша кількість часу. Не потрібно буде робити якихось складних припущень про час роботи і сподіватися, що насправді ця величина не буде перевищена. у деяких алгоритмах найгірший випадок зустрічається досить часто. Наприклад, якщо в базі даних відбувається пошук інформації, те найгіршому випадкові відповідає ситуація, коли потрібна інформація в базі даних відсутній. У деяких пошукових додатках пошук відсутньої інформації може відбуватися досить часто. характер поводження "усередненого" часу роботи часто нічим не краще поводження часу роботи для найгіршого випадку. Припустимо, що послідовність, до якої застосовується сортування методом уставок, сформована випадковим образом. Скільки часу знадобиться, щоб визначити, у яке місце підмасива A[1. . j — 1] варто помістити елемент А [j]? У середньому половина елементів підмасива A [1. . J — 1] менше, ніж А [j], а половина — більше його. Таким чином, у середньому потрібно перевірити половину елементів підмассива A[1. . j — 1] , тому tj приблизно дорівнює j/2. У результаті виходить, що середній час роботи алгоритму є квадратичною функцією від кількості вхідних елементів, тобто характер цієї залежності такий же, як і для часу роботи в найгіршому випадку. У деяких окремих випадках нас буде цікавити середній час роботи алгоритму, або його математичне чекання.

5. 3. 2 Алгоритм сортування Quick Sort • Загальний аналіз ефективності «швидкої» сортування досить важкий. Буде краще показати її обчислювальну складність, підрахувавши число порівнянь при деяких ідеальних допущеннях. Допустимо, що n – ступінь двійки, а центральний елемент розташовується точно посередині кожного списку і розбиває його на дві підсписки приблизно однакові довжини. • При першому скануванні виробляється n-1 порівнянь. У результаті створюються два підсписки розміром n/2. На наступній фазі обробка кожного підсписку вимагає приблизно n/2 порівнянь. Загальне число порівнянь на цій фазі дорівнює 2(n/2) = n. На наступній фазі обробляються чотири підсписки, що вимагає 4(n/4) порівнянь і т. д. У кінців-кінців процес розбивки припиняється після k проходів, що коли підсписки містять по одному елементі. Загальне число порівнянь приблизно дорівнює • n + 2(n/2) + 4(n/4) +. . . + n(n/n) = n +. . . + n = n * k = n * log 2 n.

Quick Sort • Для списку загального виду обчислювальна складність «швидкої» сортування дорівнює • O(n log 2 n). Ідеальний випадок, що ми тільки що розглянули, фактично виникає тоді, коли масив уже відсортований по зростанню. Тоді центральний елемент попадає точно в середину кожного підсписку. • Якщо масив відсортований по спаданню, то на першому проході центральний елемент виявляється на середині списку і міняється місцями з кожним елементом як у першому, так і в другому підсписку. Результуючий список майже відсортований, алгоритм має складність порядку O(n log 2 n).

Quick Sort • Найгіршим сценарієм для «швидкої» сортування буде той, при якому центральний елемент увесь час попадає в одноелементний підсписок, а всі інші елементи залишаються в другому підсписку. Це відбувається тоді, коли центральним завжди є найменший елемент. Розглянемо послідовність 3, 8, 1, 5, 9. • На першому проході виробляється n порівнянь, а більший підсписок містить n-1 елементів. На наступному проході цей підсписок вимагає n-1 порівнянь і дає підсписок з n-2 елементів і т. д. Загальне число порівнянь дорівнює

Quick Sort • n + n-1 + n-2 +. . . + 2 = n(n+1)/2 – 1. • Складність гіршого випадку дорівнює O(n 2), тобто не краще, ніж для сортувань вставками і вибором. Однак цей випадок є патологічним і малоймовірний на практиці. Загалом, середня продуктивність «швидкої» сортування вище, ніж у всіх розглянутих нами сортувань. • Алгоритм Quick. Sort вибирається за основу в більшості універсальних утиліт, що сортують. Якщо ви не можете упокоритися з продуктивністю найгіршого випадку, використовуйте пірамідальне сортування – більш стійкий алгоритм, складність якого дорівнює O(n log 2 n) і залежить тільки від розміру списку.

5. 3. 3 Алгоритм сортування Heap Sort • • У гіршому випадку потрібно п/2 кроків, що зрушують, вони зрушують елементи на log (n/2), log (п/2— 1), . . . , log(n-l) позицій (логарифм (по підставі 2)] «обрубується» до наступного меншого цілого). Отже, фаза сортування вимагає n-1 зрушень найбільше log(n-1), log(n-2), . . . , 1 переміщеннями. Крім того, потрібно ще n — 1 переміщень для просочування зрушеного елемента на деяку відстань вправо. Ці розуміння показують, що навіть у найгіршому з можливих випадків Heap -sort зажадає n*log n кроків. Чудова продуктивність у таких поганих випадок-одну з привабливих властивостей Heapsort. Зовсім не ясно, коли варто очікувати найгіршої (або найкращої) продуктивності. Але взагалі ж здається, що Heapsort «любить» початкові послідовності, у яких елементи більш-менш відсортовані в зворотному порядку. Тому її поводження трохи неприродне. Якщо ми маємо справу зі зворотним порядком, то фаза породження піраміди не вимагає яких-небудь переміщень. Середнє число переміщень приблизно дорівнює п/2* log(n), причому відхилення від цього значення відносно невеликі.

5. 3. 4 Алгоритм сортування Merge Sort • • Якщо алгоритм рекурсивно звертається до самого себе, час його роботи часто описується за допомогою рекурентного рівняння, або рекурентного співвідношення, у якому повний час, необхідний для рішення всієї задачі з обсягом уведення п, виражається через час рішення допоміжних підзадач. Потім дане рекурентное рівняння вирішується за допомогою визначених математичних методів, і встановлюються границі продуктивності алгоритму. Одержання рекурентного співвідношення для часу роботи алгоритму, заснованого на принципі "розділяй і пануй", базується на трьох етапах, що відповідають парадигмі цього принципу. Позначимо через Т (п) час рішення задачі, розмір якого дорівнює п. Якщо розмір задачі досить малий, скажемо, п з, де з — деяка заздалегідь відома константа, то задача вирішується безпосередньо протягом визначеного фіксованого часу, що ми позначимо через (1). Припустимо, що наша задача поділяється на а підзадач, обсяг кожної з яких дорівнює 1/b від обсягу вихідної задачі. (В алгоритмі сортування методом злиття числа а і b були рівні 2, однак нам має бути ознайомитися з багатьма алгоритмами розбивки, у яких а b). Якщо розбивка задачі на допоміжні підзадачи відбувається протягом часу D (n), а об'єднання рішень підзадач у рішення вихідної задачі — протягом часу З (n), то ми одержимо таке рекурентное співвідношення:

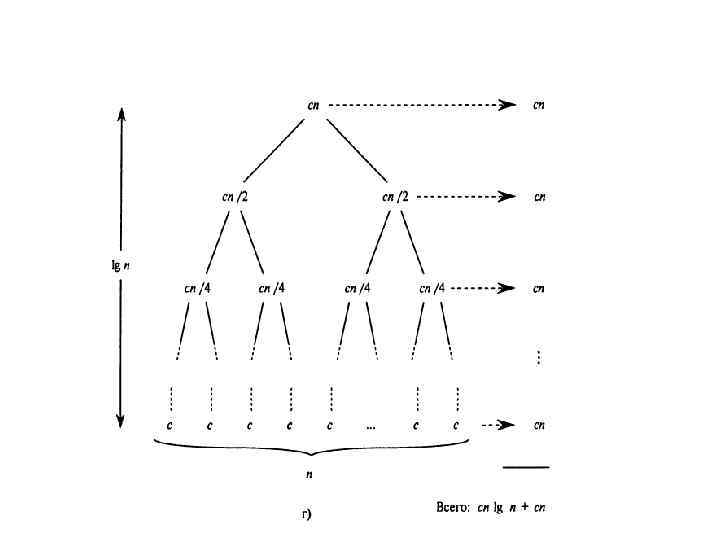
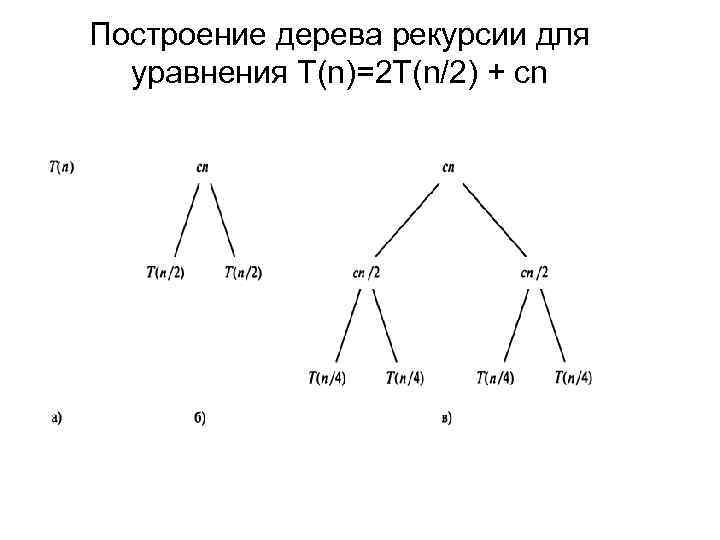Построение дерева рекурсии для уравнения T(n)=2 T(n/2) + cn