Тема 4 Стоимостная оценка риска на основе концепции

Тема 4: Стоимостная оценка риска на основе концепции Value-at-Risk (Va. R) 1. Понятие Va. R и особенности его расчета, принципы оценки рыночных рисков. 2. Методы расчета Va. R, их достоинства и недостатки.

Опыт показывает, что вероятность возникновения ситуации, приводящей к большим потерям на сравнительно устойчивом рынке довольно мала. Ориентация на такие ситуации при текущем управлении рисками, приведет к неоправданному сокращению объемов операций. Поэтому банк при решении задач текущего управления рисками должен ориентироваться на нестрессовые, динамические потери. Крупные катастрофические потери при этом целесообразно рассматривать отдельно в рамках стресс-тестинга.

Для получения нестрессовой оценки рыночного риска, имеющей практическую ценность, из рассмотрения имеет смысл исключить небольшую долю (обычно 5% или 1%) самых неблагоприятных случаев, то есть сузить интервал возможных значений случайной величины. Тогда оценкой риска будут убытки, которые возникнут в самом неблагоприятном из оставшихся 95% или 99% случаев. Ширина интервального прогноза и, следовательно, и оценка риска, зависит от длины временного горизонта и от доли отброшенных неблагоприятных случаев, то есть задаваемой вероятности того, что предсказанное значение попадет в этот интервал.

Value-at-Risk (Va. R) – денежная оценка максимальных ожидаемых потерь по открытым позициям, в течение заданного временного горизонта и для заданного уровня доверительной вероятности.

Va. R – это выраженная в данных денежных единицах (базовой валюте) оценка величины, которую не привысят ожидаемые в течение данного периода времени потери с заданной вероятностью. Показатель Va. R обычно не используется применительно к рынкам, находящимся в состоянии кризиса. Va. R – это наибольший ожидаемый убыток, обусловленный колебаниями цен на финансовых рынках, который рассчитывается: ◦ - на определенный период времени в будущем (временной горизонт); ◦ - с заданной вероятностью его не превышения (уровень доверия); ◦ - при данном предположении о характере поведения рынка (метод расчета).

Временной горизонт удержания позиции – минимальная сумма времени на принятие решения о закрытии позиции (например, вследствие ухудшающейся рыночной конъюнктуры) и времени на реализацию этого решения, с учетом ликвидности инструмента без существенного ущерба.

Глубина периодов расчета Va. R – это объем ретроспективных или симулированных данных, на основе которых рассчитывается оценка. Уровень доверия (доверительный интервал)) – вероятность наступления (или ненаступления) какого-либо события.

Доверительный интервал и временной горизонт являются ключевыми параметрами, без которых невозможны ни расчет, ни интерпретация показателя Va. R. Так, значение Va. R в 10 млн р. для временного горизонта в один день и доверительного интервала 99 % будет означать (при условии сохранения тенденций рыночной конъюнктуры): - вероятность того, что в течение следующих 24 часов мы потеряем не более чем 10 млн р. , составляет 99 %; - вероятность того, что наши убытки превысят 10 млн р. в течение ближайших суток, равна 1 %; - убытки, превышающие 10 млн р. , ожидаются в среднем один раз в 100 дней торгов.

Существуют 2 основные группы подходов к оценке Va. R: 1) «локальное оценивание» – линейная или более сложная аппроксимация функции стоимости финансового инструмента, важнейшим примером которого является параметрический дельта-нормальный метод; 2) «полное оценивание» - полный пересчет стоимости финансового инструмента без аппроксимирующих предположений. К этой группе относятся метод исторического моделирования и метод Монте-Карло.

Показатель Va. R используется в рискменеджменте в следующих целях: - для расчета лимитов по открытым позициям; - для расчета достаточности капитала и распределения капитала между направлениями бизнеса; - для оценки доходности операций с учетом риска.

Верификация моделей расчета Va. R по историческим данным - это процедура, позволяющая установить степень адекватности модели оценки рыночного риска в виде показателя Va. R реальным условиям рынка.

2. Основные методы расчета Va. R, их достоинства и недостатки. Исторически понятие Value at risk неразрывно связано с дельта нормальным методом расчета показателя, который был впервые реализован банком J. P. Morgan Chase в своей знаменитой системе Risk. Metrics, начавшей функционирование в открытом режиме с конца октября 1994 г. и получившей всеобщее признание в качестве отраслевого стандарта.

Дельта-нормальный метод расчета величины Va. R позволяет Получить оценку Va. R в замкнутом виде. В его основе лежит посылка о нормальном законе распределения логарифмических доходностей факторов рыночного риска. Предположение о нормальном распределении изменений факторов риска значительно облегчает нахождение величины Va. R, т. к. в этом случае распределение доходностей инструментов, являющихся линейными комбинациями факторов риска, также будет нормальным. Это фундаментальное свойство будет сохраняться для любого портфеля, состоящего из инструментов с линейными ценовыми характеристиками, как, например, акций или валют.

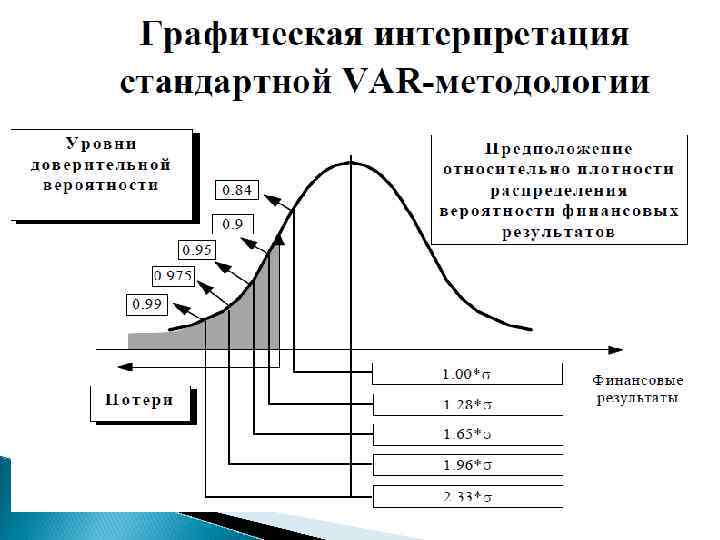
В случае нормально распределенной случайной величины доверительный интервал (1 -α) всегда характеризуется единственным параметром – квантилем ( ), который показывает положение искомого значения случайной величины (симметрично в обоих хвостах распределения) относительно среднего ( ), выраженного в количестве стандартных отклонений доходности портфеля ( ).

Статистическая оценка максимальных отрицательных отклонений рыночной стоимости портфеля из одного актива (однородных инструментов) за период Т дней удержания позиции определяется по формуле: где - рыночная стоимость на дату t портфеля данного актива; - статистическая оценка математического ожидания функции доходности Rt

◦ - квантиль отсечения для α (ДАЛЕЕ ГРАФИК И ТАБЛИЦА); ◦ - статистическая оценка дисперсии (среднеквадратичного отклонения) функции доходности; ◦ - доходность актива за период Т дней удержания актива; ◦ , - рыночная цена актива в момент времени t и t-Т.

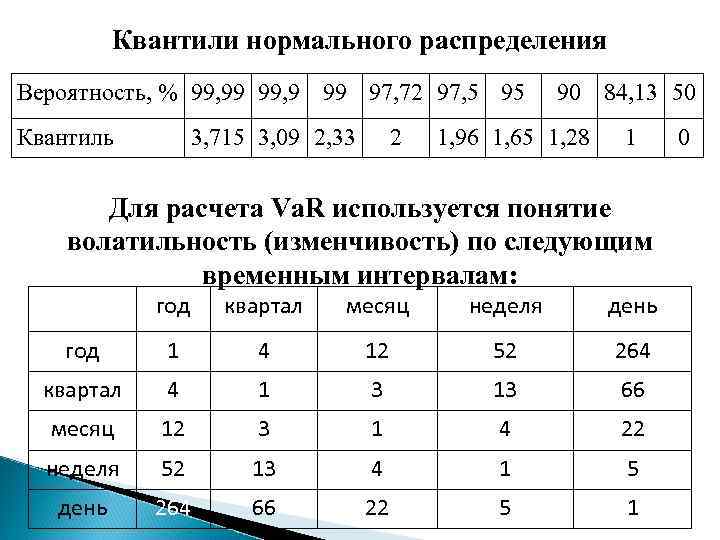Квантили нормального распределения Вероятность, % 99, 99 99, 9 99 97, 72 97, 5 95 Квантиль 3, 715 3, 09 2, 33 2 90 84, 13 50 1, 96 1, 65 1, 28 1 Для расчета Va. R используется понятие волатильность (изменчивость) по следующим временным интервалам: год квартал месяц неделя день год 1 4 12 52 264 квартал 4 1 3 13 66 месяц 12 3 1 4 22 неделя 52 13 4 1 5 день 264 66 22 5 1 0

Параметрический метод :

Достоинства ДНМ: - сравнительная простота реализации; - сравнительно небольшие затраты на сбор первичных данных и вычисления; - приемлемая точность в большинстве случаев практического применения.

Недостатки ДНМ: - низкая точность оценки риска нелинейных инструментов, таких как опционы. Он измеряет чувствительность инструмента к риску только посредством изменения цены и базисного актива, тогда как для нелинейного инструмента важную роль играет выпуклость и чувствительность к другим факторам риска. - из-за отклонения на краях распределения плотности вероятностей от нормального распределения оценки Va. R, рассчитанные на основе нормального распределения, оказываются заниженными или завышенными (в зависимости от величины уровня доверия); - игнорирование риска одиночных событий, приводящих к аномальным убыткам и не происходящих достаточно часто, чтобы быть представленными в последних исторических данных.

Метод исторического моделирования Относится к группе методов полного оценивания и является непараметрическим. Он основан на предположении о стационарности поведения рыночных цен в ближайшем будущем. Сначала выбирается период времени глубины Т (например, 200 торговых дней), за который отслеживаются исторические изменения (например, дневные) цен Р всех N входящих в портфель активов:

Для каждого из этих Т сценариев изменений моделируется гипотетическая цена каждого актива в будущем как его текущая цена плюс прирост цены, соответствующий данному сценарию: Затем производится полная переоценка всего текущего портфеля по ценам, смоделированным на основе исторических сценариев, и для каждого сценария вычисляется, насколько изменилась бы стоимость портфеля:

После этого полученные Т изменений портфеля ранжируются по убыванию (от самого большого прироста до самого большого убытка), которые можно пронумеровать от 1 до Т. В соответствии с желаемым уровнем доверия (1 -α) величина Va. R определяется как такой максимальный убыток, который не превышается в (1 -α)Т случаях, т. е. Va. R равен абсолютной величине изменения с номером, равным целой части числа (1 -α)Т.

Достоинства МИМ: - Отсутствие предположений о нормальном распределении доходностей факторов риска или какой-либо другой стахостической модели динамики цен на рынке, кроме реально наблюдавшейся в прошлом; - Хорошая точность оценки риска нелинейных инструментов; - Простота полной переоценки портфеля, осуществляемой по историческим сценариям; - Отсутствие риска использования ошибочной модели для оценки стоимости инструментов; - Интуитивная простота и наглядность.

Недостатки МИМ: - Использование только одной траектории эволюции цен; - Несоблюдение в реальности базовой посылки метода о том, что прошлое может служить хорошей моделью будущего; - Высокая вероятность ошибок измерения при малой глубине исторической ретроспективы; - Игнорирование различий между старыми и последними наблюдениями, тогда как удаление из выборки наиболее старых наблюдений может резко улучшить точность модели; - Большой объем вычислений для крупных диверсифицированных портфелей при том, что агрегирование (например, использование одной дельты для различных инструментов) может снизить преимущества полного оценивания.

Метод Монте-Карло Моделирование случайных процессов (траектории цен) с заданными характеристиками. В отличие от метода исторического моделирования, в методе Монте-Карло изменения цен активов генерируются псевдослучайным образом в соответствии с заданными параметрами распределения, например, математическим ожиданием и волатильностью.

Траектория цен – это последовательность псевдослучайным образом смоделированных цен, начиная от текущей цены и заканчивая ценой на некотором конечном шаге (например, на тысячном или десятитысячном. Чем больше число шагов, тем выше точность метода). Затем производится полная переоценка портфеля по цене последнего шага и расчет изменения его стоимости для каждого сценария. Оценка Va. R производится по распределению изменений стоимости портфеля. Генерация случайных чисел в методе Монте-Карло состоит из двух шагов. Сначала можно воспользоваться генератором случайных чисел, равномерно распределенных на интервале между О и 1. Затем, используя как аргументы полученные случайные числа, вычисляют значения функций моделируемых распределений.

Существует вариант метода Монте-Карло, при котором для моделирования цен используются непосредственные исторические данные. Подобно методу исторического моделирования, на основе ретроспективы моделируются гипотетические цены, но их последовательность не является единственной и не ограничена глубиной периода ретроспективы, поскольку выборка производится с возвращением, т. е. возмущение из исторических данных выбирается случайным образом, и каждый раз в выборе участвуют все данные, что позволяет рассмотреть не какуюлибо одну траекторию цен (сценарий), а сколь угодно много, что, как правило, повышает точность оценок.

Достоинства метода Монте-Карло - Высокая точность расчетов; - Высокая точность применительно к инструментам с нелинейными ценовыми характеристиками; - Возможность моделирования любых исторических и гипотетических распределений, учет эффекта «толстых хвостов» и скачков цен.

Недостатки метода Монте-Карло - Высокая сложность моделей и соответственно высокий риск неадекватности моделей; - Высокие требования к вычислительной мощности и значительные затраты времени на проведение расчетов.