Тема 4 Сортировка массивов 1 2 3 4

Тема 4. Сортировка массивов 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. Оценка сложности алгоритма Историческая справка Обзор методов сортировок Сортировка методом простого выбора Пирамидальная сортировка Сортировка вставками Метод Дональда Шелла Метод простого обмена Шейкер-сортировка Быстрая сортировка Анализ и сравнение методов

1. Оценка сложности алгоритма Алгоритм — это понятное и точное предписание исполнителю выполнить конечную последовательность команд, приводящую от исходных данных к искомому результату. данные данные м-N алгорит м результат . . . р алг о 3 р лго а и тм - 2 тм и Под эффективностью понимается требование: не только весь алгоритм, но и каждый шаг его должны быть такими, чтобы исполнитель был способен выполнить их за конечное разумное время. 2

Сложность алгоритма — количество элементарных шагов в вычислительном процессе этого алгоритма. Вычислительным процессом, порожденным алгоритмом, называется последовательность шагов алгоритма, пройденных при исполнении этого алгоритма. Временная сложность алгоритма — это время Т, необходимое для его выполнения. Оно равно произведению числа элементарных действий k на среднее время t выполнения одного действия: 3

Пусть для алгоритма А: • размерность (объем обрабатываемых алгоритмом данных) - n. • время выполнения алгоритма - T(n) • f — некую функцию от t. Будем говорить, что T(n) алгоритма имеет порядок роста f(n), или, по-другому, алгоритм имеет теоретическую сложность O(f(n)), если найдутся такие константы c 1, c 2>0 и число n 0, что c 1 f(n) < c 2 f(n) при всех n n 0. Здесь предполагается, что функция f(n) неотрицательна, по крайней мере при n n 0. Если для T(n) выполняется условие T(n) < cf(n), то говорят, что алгоритм имеет теоретическую сложность O(n). Примеры • алгоритм, выполняющий только операции чтения данных и занесения их в оперативную память, имеет линейную сложность O(n) • сложность алгоритма умножения матриц (таблиц) размера n n будет уже кубической O(n 3) , так как для вычисления каждого элемента результирующей матрицы требуется n умножений и n - 1 сложений, а всего этих элементов n 2. формула умножения матриц: для 4

2. Историческая справка В словарях слово “сортировка” (sorting) определяется как “распределение, отбор по сортам; деление на категории”. • 1 известным примером длинного перечня элементов, упорядоченных для облегчения поиска, является знаменитая вавилонская таблица обратных величин (~200 г. до н. э. ). В ней изображено более 500 обратных величин шестидесятиричных чисел и обратных им величин, причем, отсортированных величин. • В довольно древние времена греки использовали буквы для обозначения чисел: - 1, - 2, - 3. • Библейские псалмы содержат стихи, следующие друг за другом в строго алфавитном порядке: первый стих начинается с “алефа”, второй - с “бета” и т. д.

Использование алфавитного порядка для слов целиком • Некоторые документы ( ~ 300 г. до н. э. ), найденные на островах Эгейского моря, содержат списки членов нескольких религиозных общин, упорядоченных только по первой букве. • Греческие папирусы (134 - 135 г. н. э. ) содержат фрагменты счетов, в которых фамилии налогоплательщиков упорядочены по 2 -м первым буквам. • Джованни Генуэзский (1286 г. ) объясняет правило, по которому составлены слова в его словаре. Он приводит примеры ситуаций, когда порядок определяется по 1, 2, . . . , 6 буквам.

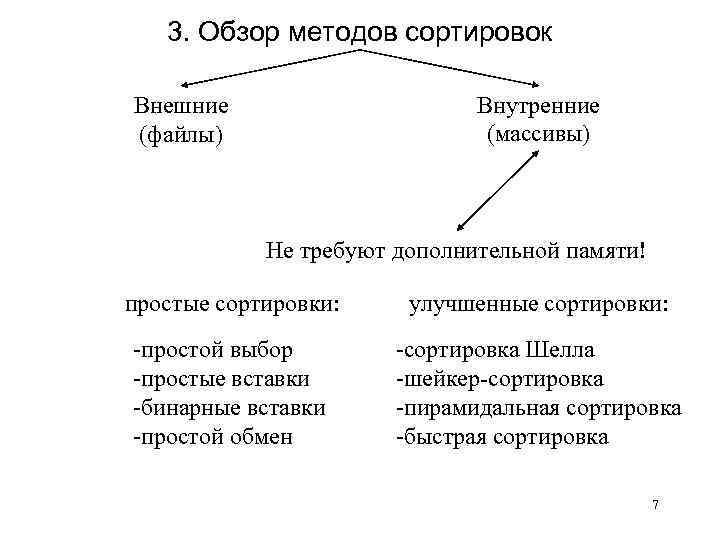3. Обзор методов сортировок Внутренние (массивы) Внешние (файлы) Не требуют дополнительной памяти! простые сортировки: улучшенные сортировки: -простой выбор -простые вставки -бинарные вставки -простой обмен -сортировка Шелла -шейкер-сортировка -пирамидальная сортировка -быстрая сортировка 7

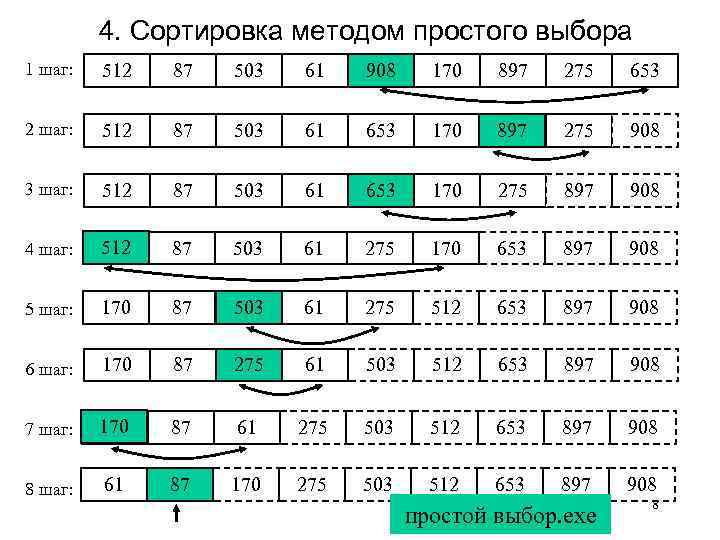4. Сортировка методом простого выбора 1 шаг: 512 87 503 61 908 170 897 275 653 2 шаг: 512 87 503 61 653 170 897 275 908 3 шаг: 512 87 503 61 653 170 275 897 908 4 шаг: 512 503 87 503 61 275 170 653 897 908 5 шаг: 170 87 512 503 61 275 512 653 897 908 6 шаг: 170 87 275 61 503 512 653 897 908 7 шаг: 170 87 61 275 503 512 653 897 908 8 шаг: 61 87 170 275 503 512 653 897 908 простой выбор. exe 8

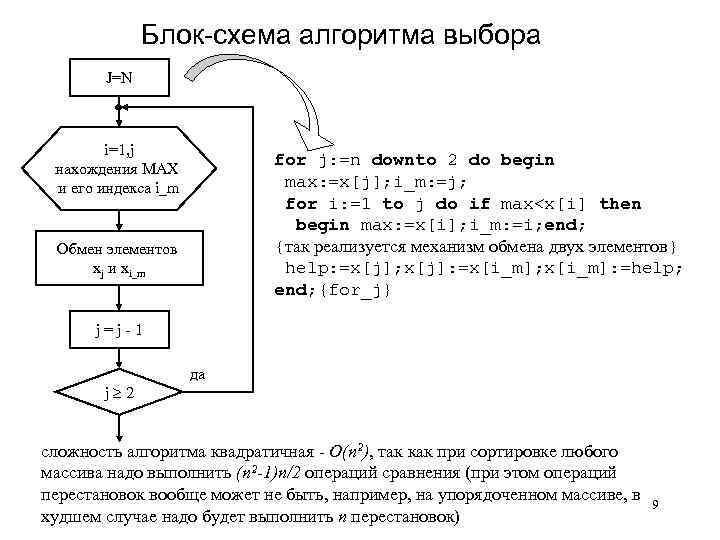Блок-схема алгоритма выбора J=N i=1, j нахождения MAX и его индекса i_m for j: =n downto 2 do begin max: =x[j]; i_m: =j; for i: =1 to j do if max

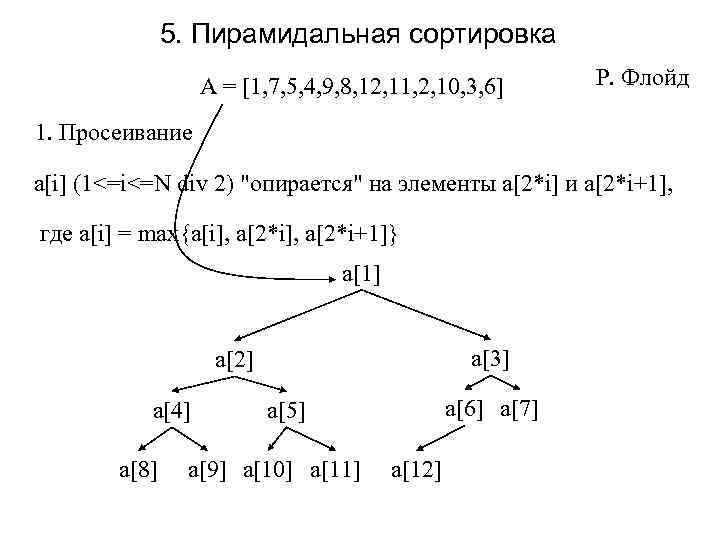5. Пирамидальная сортировка A = [1, 7, 5, 4, 9, 8, 12, 11, 2, 10, 3, 6] Р. Флойд 1. Просеивание a[i] (1<=i<=N div 2) "опирается" на элементы a[2*i] и a[2*i+1], где a[i] = max{a[i], a[2*i+1]} a[1] a[3] a[2] a[4] a[8] a[6] a[7] a[5] a[9] a[10] a[11] a[12]

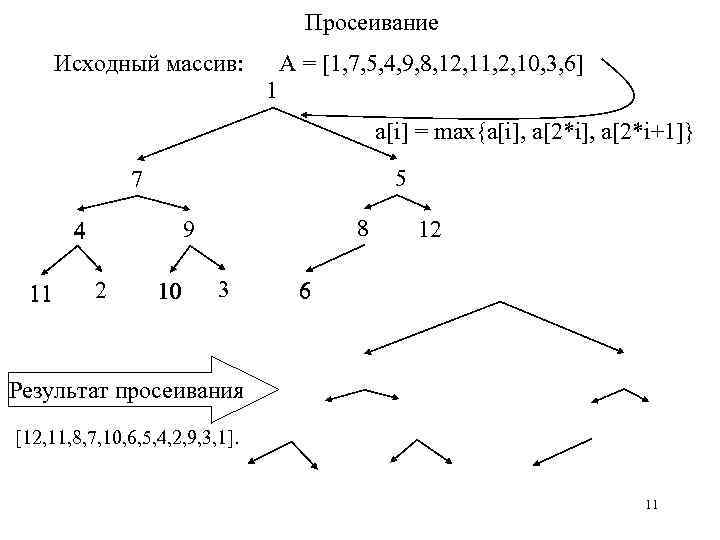Просеивание A = [1, 7, 5, 4, 9, 8, 12, 11, 2, 10, 3, 6] Исходный массив: 1 a[i] = max{a[i], a[2*i+1]} 5 7 11 8 9 4 2 10 3 12 6 Результат просеивания [12, 11, 8, 7, 10, 6, 5, 4, 2, 9, 3, 1]. 11

Алгоритм пирамидальной сортировки 0 -й шаг: Превратить исходный массив в пирамиду (с помощью просеивания). 1 -й шаг: Для N-1 элементов, начиная с последнего, производить следующие действия: - поменять местами очередной "рабочий" элемент с первым; - просеять (новый) первый элемент, не затрагивая, однако, уже отсортированный хвост последовательности (элементы с i-го по N-й). 12

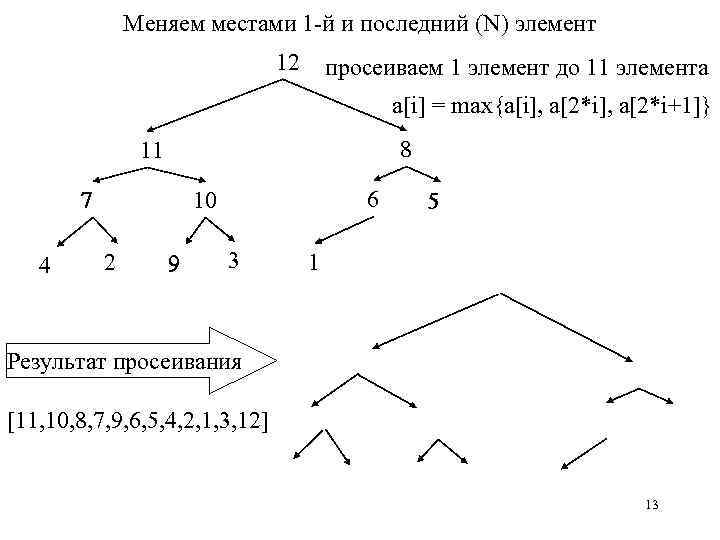Меняем местами 1 -й и последний (N) элемент 12 просеиваем 1 элемент до 11 элемента a[i] = max{a[i], a[2*i+1]} 8 11 7 4 6 10 2 9 3 5 1 Результат просеивания [11, 10, 8, 7, 9, 6, 5, 4, 2, 1, 3, 12] 13

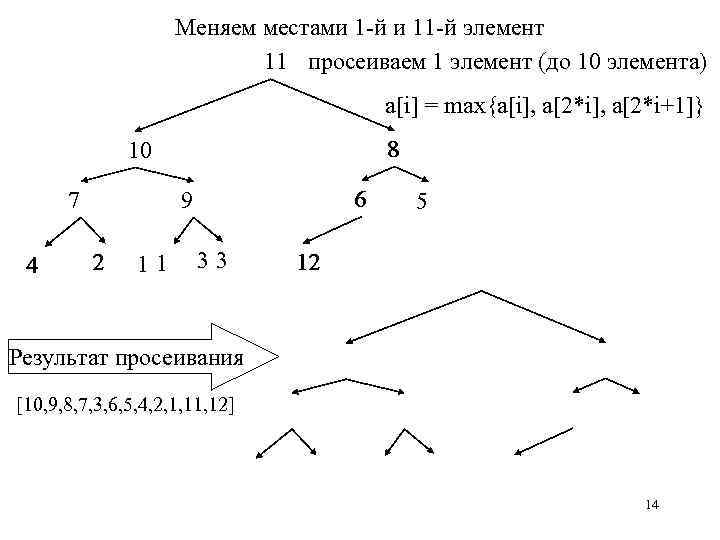Меняем местами 1 -й и 11 -й элемент 11 просеиваем 1 элемент (до 10 элемента) a[i] = max{a[i], a[2*i+1]} 8 10 7 4 6 9 2 11 33 5 12 Результат просеивания [10, 9, 8, 7, 3, 6, 5, 4, 2, 1, 12] 14

Оставшиеся шаги: [10, 9, 8, 7, 3, 6, 5, 4, 2, 1, 12] [1, 9, 8, 7, 3, 6, 5, 4, 2, 10, 11, 12] [9, 7, 8, 4, 3, 6, 5, 1, 2, 10, 11, 12] [2, 7, 8, 4, 3, 6, 5, 1, 9, 10, 11, 12] [8, 7, 6, 4, 3, 2, 5, 1, 9, 10, 11, 12] [1, 7, 6, 4, 3, 2, 5, 8, 9, 10, 11, 12] [7, 4, 6, 1, 3, 2, 5, 8, 9, 10, 11, 12] [5, 4, 6, 1, 3, 2, 7, 8, 9, 10, 11, 12] [6, 4, 5, 1, 3, 2, 7, 8, 9, 10, 11, 12] [2, 4, 5, 1, 3, 6, 7, 8, 9, 10, 11, 12] [5, 4, 2, 1, 3, 6, 7, 8, 9, 10, 11, 12] [3, 4, 2, 1, 5, 6, 7, 8, 9, 10, 11, 12] [4, 3, 2, 1, 5, 6, 7, 8, 9, 10, 11, 12] [1, 3, 2, 4, 5, 6, 7, 8, 9, 10, 11, 12] [3, 1, 2, 4, 5, 6, 7, 8, 9, 10, 11, 12] [2, 1, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12] Меняем местами a[1] и a[10]: Просеиваем элемент a[1]: Меняем местами a[1] и a[9]: Просеиваем элемент a[1]: Меняем местами a[1] и a[8]: Просеиваем элемент a[1]: Меняем местами a[1] и a[7]: Просеиваем элемент a[1]: Меняем местами a[1] и a[6]: Просеиваем элемент a[1]: Меняем местами a[1] и a[5]: Просеиваем элемент a[1]: Меняем местами a[1] и a[4]: Просеиваем элемент a[1]: Меняем местами a[1] и a[3]: Просеивать уже ничего не нужно Меняем местами a[1] и a[2]: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12] Просеивать ничего не нужно, сортировка закончена. Эффективность -N*log N 15

просеивание. . . for i: = (N div 2) downto 1 do begin j: = i; while j<=(N div 2) do begin k: = 2*j; if (k+1<=N) and (a[k]a[j] then begin x: = a[j]; a[j]: = a[k]; a[k]: = x; j: = k end else break end; . . . 16

сортировка. . . for i: = N downto 2 do begin x: = a[1]; a[1]: = a[i]; a[i]: = x; j: = 1; while j<=((i-1) div 2) do begin k: = 2*j; if (k+1<=i-1) and (a[k]a[j] then begin x: = a[j]; a[j]: = a[k]; a[k]: = x; j: = k end else break end; . . . 17

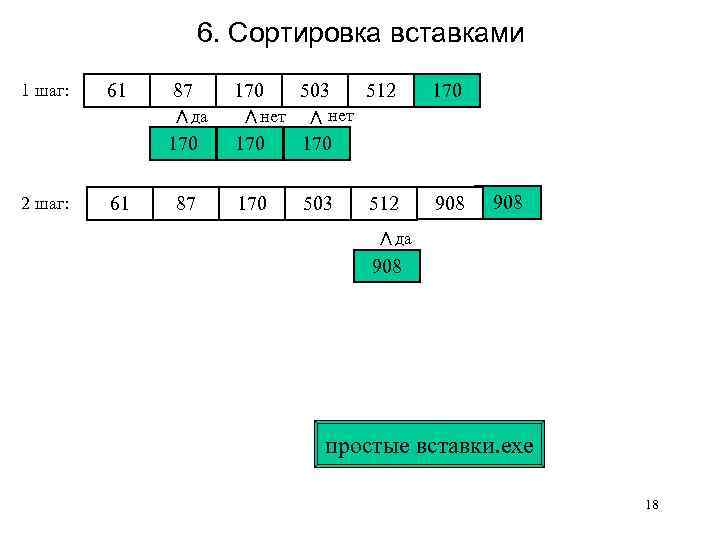6. Сортировка вставками 1 шаг: 61 87 170 512 908 170 87 170 503 908 да > 61 170 > 170 2 шаг: 512 нет > нет 503 512 > да 170 503 908 простые вставки. exe 18

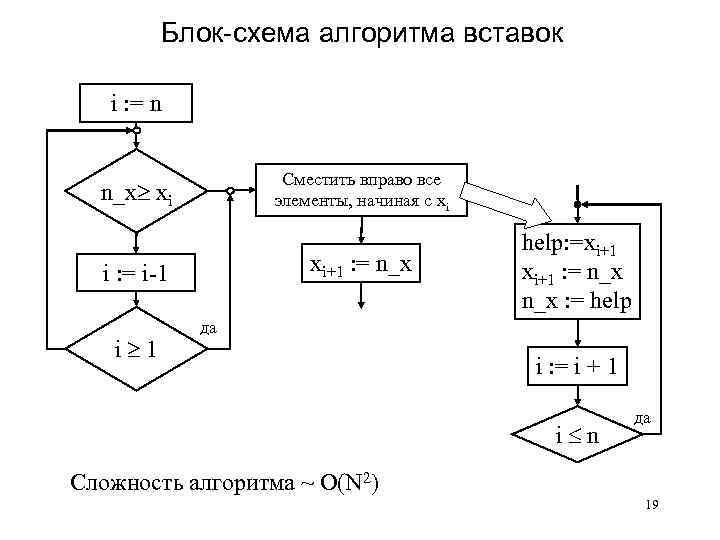Блок-схема алгоритма вставок i : = n Сместить вправо все элементы, начиная с xi n_x xi xi+1 : = n_x i : = i-1 i 1 help: =xi+1 : = n_x : = help да i : = i + 1 i n да Сложность алгоритма ~ O(N 2) 19

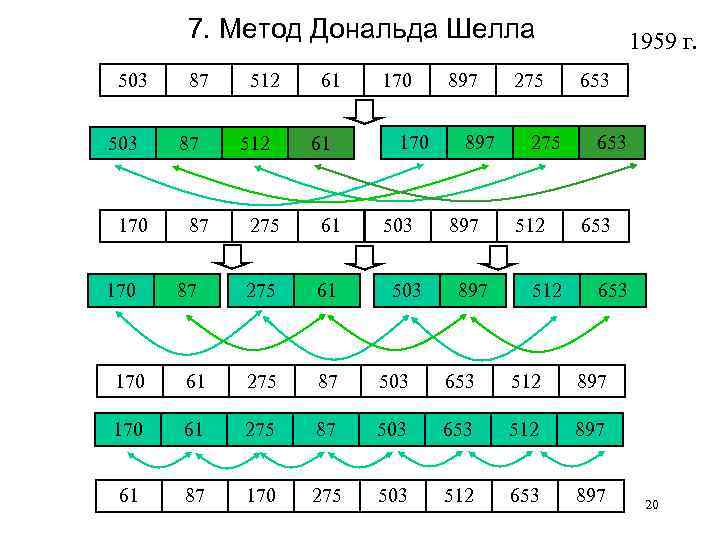7. Метод Дональда Шелла 503 170 87 87 512 61 61 275 61 170 503 897 897 275 512 1959 г. 653 653 170 61 275 87 503 653 512 897 61 87 170 275 503 512 653 897 20

Подбор шага для алгоритма Шелла Кнут: h 1 = 1, hs+1 = 3 hs + 1, остановиться на ht, когда ht+2 N (количество элементов). Затраты пропорциональны: ~ O( N 3. 2). 21

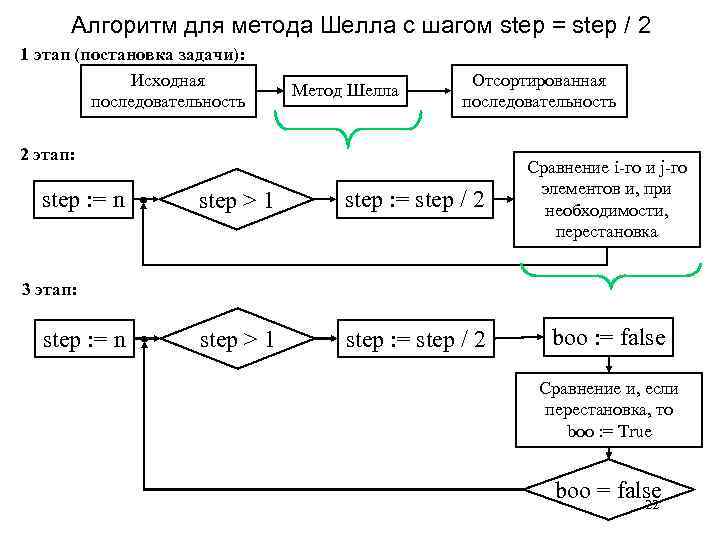Алгоритм для метода Шелла с шагом step = step / 2 1 этап (постановка задачи): Исходная последовательность Метод Шелла Отсортированная последовательность 2 этап: step : = n step > 1 step : = step / 2 Сравнение i-го и j-го элементов и, при необходимости, перестановка step > 1 step : = step / 2 boo : = false 3 этап: step : = n Сравнение и, если перестановка, то boo : = True boo = false 22

Индексы сравниваемых элементов 4 этап: шаг step=N/2 x 1, x 2, …, xn/4+1, xn/4+2, …, xn/2+1, xn/2+2, …x 3 n/4, x 3 n/4+1, …xn индексы сравниваемых элементов 1 N/2 + 1 2 N/2 + 2. . . N/2 N/2+N/2, т. е. N при этом индекс сравниваемых элементов ai и аj - i = 1 N/2, j = N/2 + i x 1, x 2, …, xn/4+1, xn/4+2, …, xn/2+1, xn/2+2, …x 3 n/4, x 3 n/4+1, …xn шаг step=N/4 индексы сравниваемых элементов 1 N/4 + 1 N/2 + 1 2 N/4 + 2 N/2 + 2. . N/4 N/2 3/4 N + 1 3/4 N + 2. . . N при этом индекс сравниваемых элементов ai и аj - i = 1 3 N/4, j = N/4 + i Общий вид зависимости номеров сравниваемых элементов: j = i + step при i = 1 N - step. 23

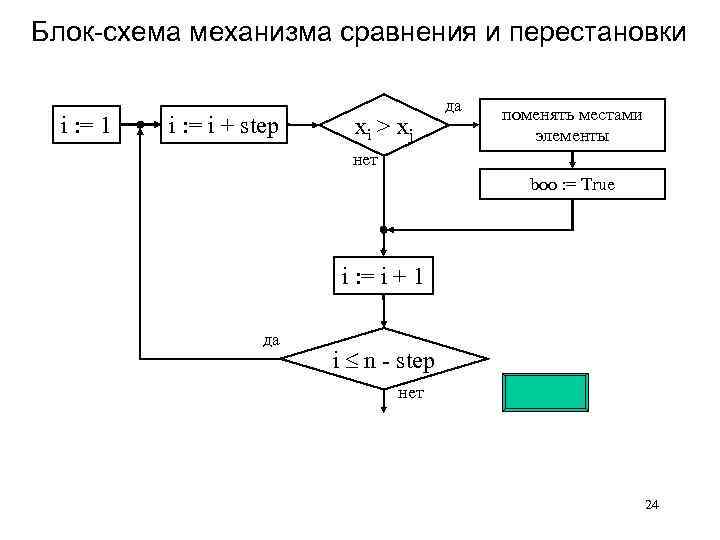Блок-схема механизма сравнения и перестановки i : = 1 i : = i + step xi > xj да поменять местами элементы нет boo : = True i : = i + 1 да i n - step нет 24

8. Метод простого обмена 44 92 92 55 44 67 67 67 12 55 44 55 55 42 12 55 44 44 92 42 12 42 42 18 67 42 12 18 6 18 18 18 12 67 6 6 25

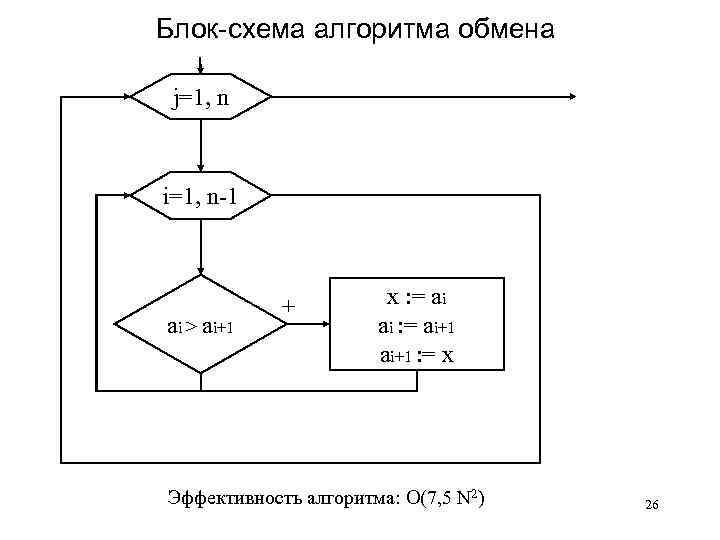Блок-схема алгоритма обмена j=1, n i=1, n-1 ai > ai+1 + x : = ai ai : = ai+1 : = x Эффективность алгоритма: O(7, 5 N 2) 26

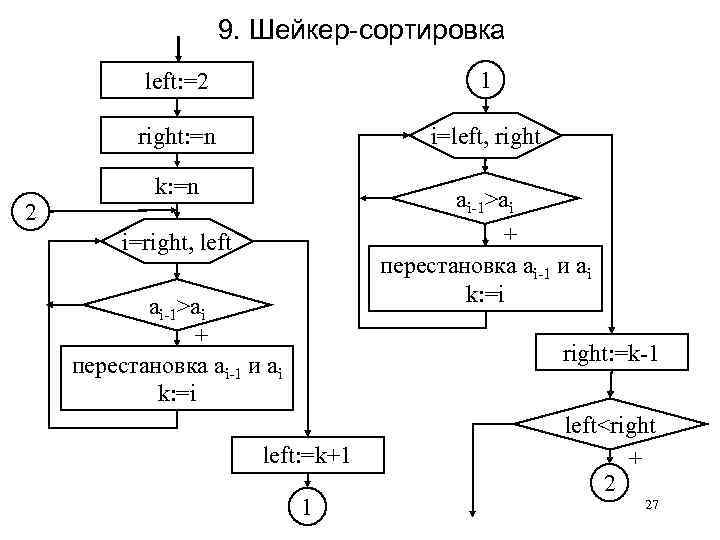9. Шейкер-сортировка left: =2 right: =n 2 1 i=left, right k: =n ai-1>ai + перестановка ai-1 и ai k: =i i=right, left ai-1>ai + перестановка ai-1 и ai k: =i right: =k-1 left: =k+1 1 left

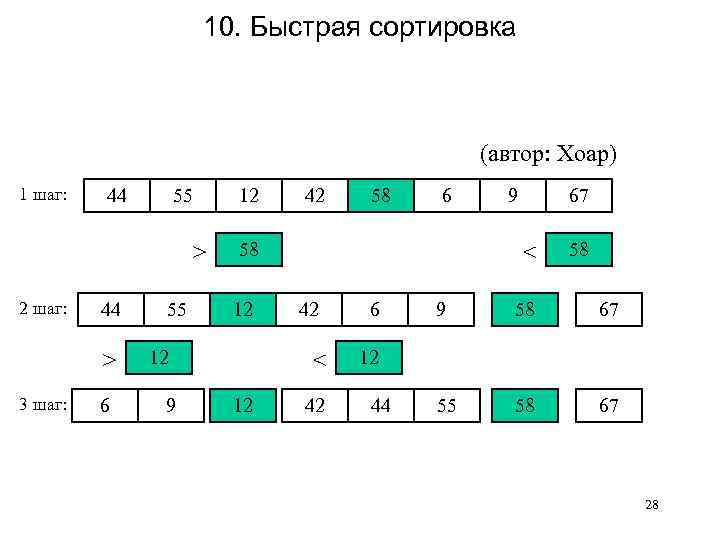10. Быстрая сортировка (автор: Хоар) 1 шаг: 44 55 12 > 2 шаг: 44 > 3 шаг: 6 55 58 6 58 12 12 9 42 67 < 42 < 12 9 42 6 58 9 58 67 55 58 67 12 44 28

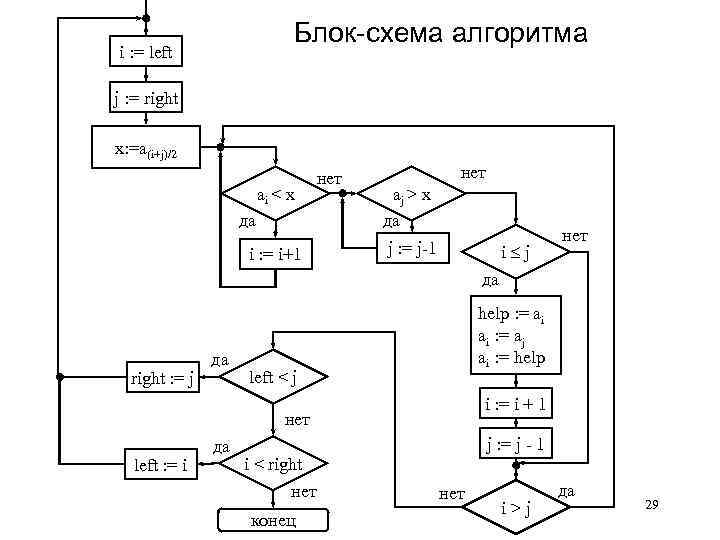Блок-схема алгоритма i : = left j : = right x: =a(i+j)/2 ai < x да i : = i+1 нет aj > x да j : = j-1 i j нет да right : = j да help : = ai ai : = aj ai : = help left < j i : = i + 1 нет left : = i да j : = j - 1 i < right нет конец нет i>j да 29

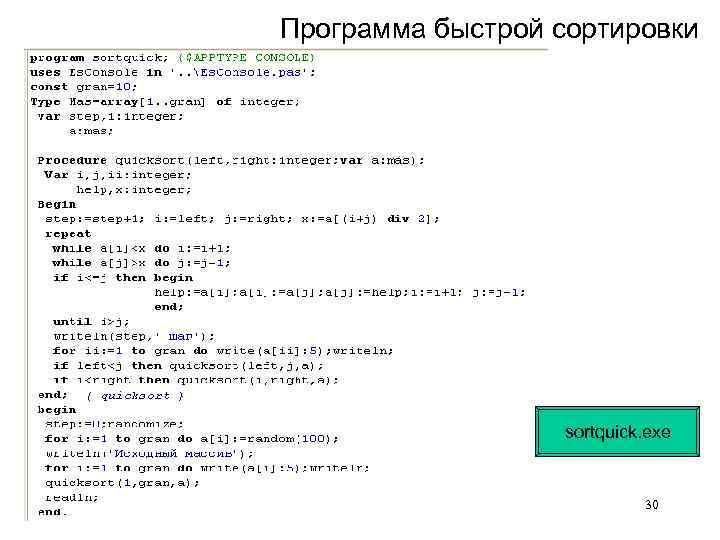Программа быстрой сортировки sortquick. exe 30

11. Анализ и сравнение методов Сложность алгоритма (n – размерность массива) Точные аналитические формулы: § метод прямого выбора – O(2, 5 n 2); § метод прямых вставок – O(2, 25 n 2); § метод прямого обмена – O(7, 5 n 2); Приближенные формулы: § метод пирамидальной сортировки ~ O(n*log 2 n) § метод Шелла ~ O(n 1. 2); § быстрая сортировка ~ О(n·ln n) Кнут «Искусство программирования для ЭВМ» Экспериментальные исследования: 1) Улучшение методов прямого включения почти ничего не дает. 2) Пузырьковая сортировка – самая медленная. 3) Шейкер-сортировка плоха по сравнению с прямыми вставками и прямым выбором. Н. Вирт «Алгоритмы и структуры данных»

Вопросы по теме «Сортировка массивов» 1. 2. 3. 4. 5. К какому методу сортировки можно отнести утверждение: «Для использования данного метода можно вначале располагать всего одним элементом массива» В каком методе используется принцип сравнения: всегда сравниваются между собой только соседние элементы. Для какого метода сортировки характерно сравнивание элементов, расположенных «сравнительно далеко» друг от друга? Для какого метода характерно уменьшение числа рассматриваемых элементов на каждом шаге алгоритма? Для реализации какого метода характерно использование механизма рекурсии?