Тема 4 Применение функционального анализа для решения прикладных

Тема 4. Применение функционального анализа для решения прикладных задач В экономической теории используется весьма широкий спектр функций – линейные , степенные, тригонометрические и др. Используются функции как одной, так и многих переменных. Элементы функционального анализа применяются для анализа эффективности размещения вкладов. Для анализа финансовых операций широко применяются методы математической статистики, в том числе – анализ временных рядов. В экономической теории наиболее часто используются: 1. Функции полезности (предпочтений)- зависимость полезности некоторого действия от интенсивности этого действия 2. Функции спроса, потребления и предложения 3. Функции Торнквиста – зависимость спроса от доходов 4. Функции Кобба- Дугласа 5. Производственные функции: зависимость результата производственной деятельности от факторов. К производственным функциям относятся: Ш Функция выпуска – зависимость объема производства от наличия или потребления ресурсов Ш Функция издержек – зависимость издержек производства от объема продукции Ш Функции Кобба- Дугласа

4. 1. Функция полезности. Задача потребительского выбора Постановка задачи. Потребитель располагает суммой I (I - доход, расход), которую полностью тратит на приобретение благ (товаров). Учитывая структуру цен , доход I, и собственные предпочтения, потребитель приобретает определенное количество благ. Цены благ считаются заданными. Математическая модель поведения потребителя получила название модель потребительского выбора. На множестве потребительских наборов определена функция полезности потребителя U. Значение U на потребительском наборе равна потребительской оценке этого набора. Если набор А предпочтительнее набора В, то U(А) > U(B). Задача потребительского выбора –выбор такого потребительского набора, который максимизирует его функцию полезности при заданном бюджетном ограничении. Дальнейшее изложение ведется на потребительском наборе из двух благ x 1 и x 2

4. 1 Функция полезности. Задача потребительского выбора Функция полезности удовлетворяет следующим условиям 1. Возрастание потребления одного продукта при постоянном потреблении второго ведет к росту потребительской оценки 2. Предельная полезность каждого продукта уменьшается, если объем его потребления растет 3. Предельная полезность каждого продукта увеличивается, если растет количество другого продукта. В этом случае продукт, количество которого фиксировано становится относительно дефицитным, дополнительная его единица становиться более ценной Линии, соединяющие потребительские наборы (x 1 , x 2) имеющие один и тот же уровень функции полезности, называются линиями безразличия. Множество линий безразличия называется картой безразличия. Согласно условиям 1. . 3, линия безразличия убывающая, строго выпуклая к началу координат линия

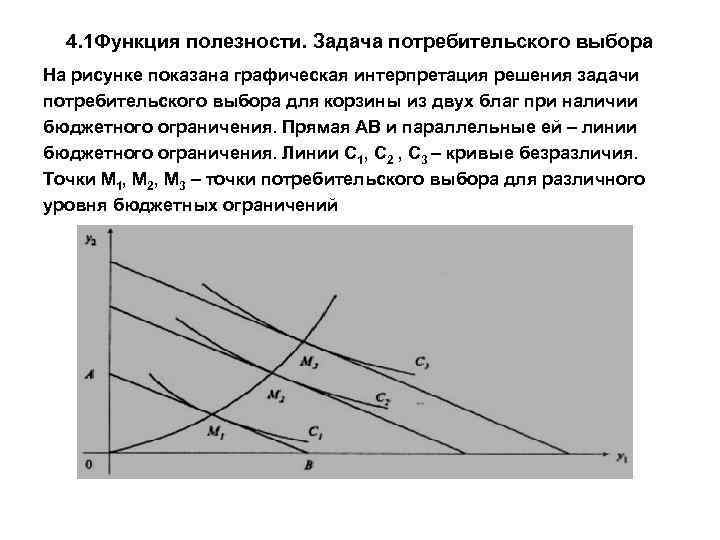4. 1 Функция полезности. Задача потребительского выбора На рисунке показана графическая интерпретация решения задачи потребительского выбора для корзины из двух благ при наличии бюджетного ограничения. Прямая АВ и параллельные ей – линии бюджетного ограничения. Линии С 1, С 2 , С 3 – кривые безразличия. Точки М 1, М 2, М 3 – точки потребительского выбора для различного уровня бюджетных ограничений

4. 1. Решение задачи потребительского выбора. Рассмотрим задачу в случае двух благ, двух переменных х1 и х2. Модель задачи Набор (x 1 0, x 2 0), являющийся решением потребительского выбора, называется оптимальным для потребителя. С математической точки зрения это точка локального рыночного равновесия покупателя. Математически доказано, что отношение предельных полезностей (первых частных производных функции полезности U) равно отношению рыночных цен

4. 1. Решение задачи потребительского выбора. В общем случае решение задачи потребительского выбора приводит к тому, что отношение предельных полезностей двух благ равно отношению их рыночных цен В частном случае модели Р. Стоуна получено, что доход I делится на n равных частей,

4. 1. Задача потребительского выбора. Пример Пусть Тогда система уравнений примет вид а ее решение равно Т. о. расход на каждое благо составляет половину общего дохода потребителя

4. 2. Равновесие спроса и предложения Спрос на товар D (Demand)- потребность в определенном количестве товара, ограниченная действующими ценами и платежеспособностью потребителя. Предложение товара S (Supply) – количество товара, которое может быть представлено на рынке для продажи по данной цене Цена P (Price)– цена предложения или спроса Предложение товара - некоторая функция P = f (S) предложения S от его цены P, называемой кривой предложения, в случае линейной зависимости Зависимость спроса (D) от цены P называют кривой спроса. В случае линейной зависимости Обычно кривые спроса и предложения строятся на плоскости т. о. , что по оси У откладывается цена P, по оси Х – спрос D или предложение S. Тогда ось Х обозначается общей переменной Q

Равновесие спроса и предложения • Кривая предложения функция возрастающая, а>0 • Кривая спроса функция убывающая, с<0 • Точка пересечения кривых спроса и предложения (точка (P 0, Q 0)) называется точкой равновесия, а соответствующая ей цена P 0 - равновесной ценой.

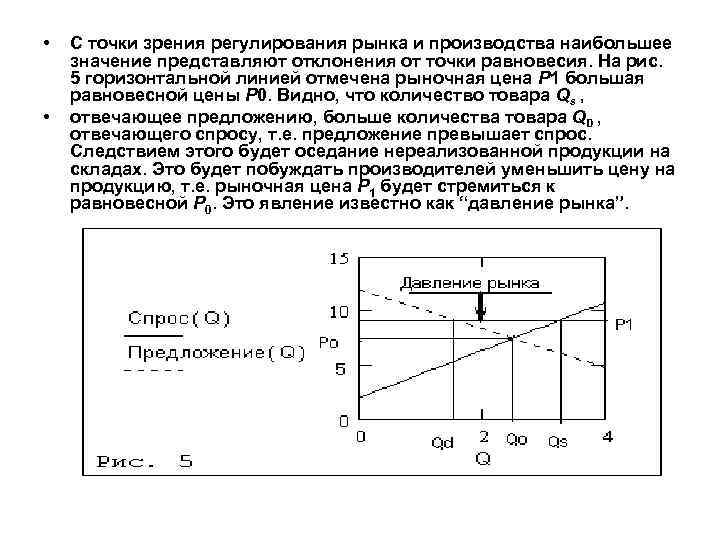• • С точки зрения регулирования рынка и производства наибольшее значение представляют отклонения от точки равновесия. На рис. 5 горизонтальной линией отмечена рыночная цена P 1 большая равновесной цены P 0. Видно, что количество товара Qs , отвечающее предложению, больше количества товара QD , отвечающего спросу, т. е. предложение превышает спрос. Следствием этого будет оседание нереализованной продукции на складах. Это будет побуждать производителей уменьшить цену на продукцию, т. е. рыночная цена P 1 будет стремиться к равновесной P 0. Это явление известно как “давление рынка”.

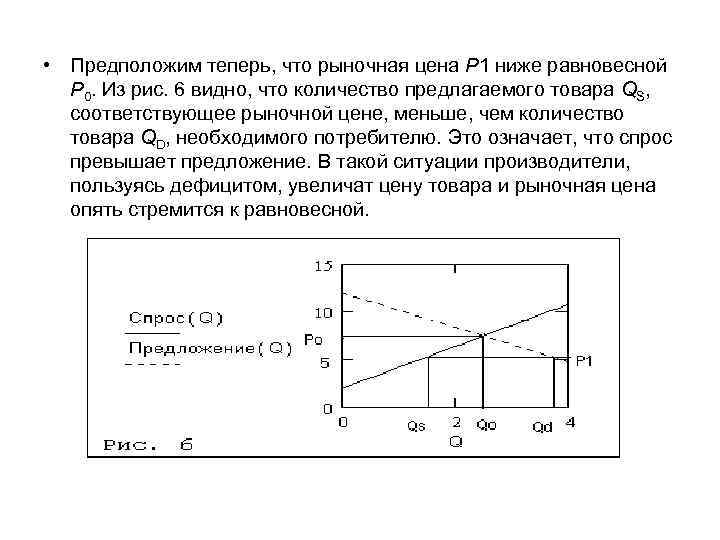• Предположим теперь, что рыночная цена P 1 ниже равновесной P 0. Из рис. 6 видно, что количество предлагаемого товара QS, соответствующее рыночной цене, меньше, чем количество товара QD, необходимого потребителю. Это означает, что спрос превышает предложение. В такой ситуации производители, пользуясь дефицитом, увеличат цену товара и рыночная цена опять стремится к равновесной.

4. 3. Функции Торнквиста. Зависимость спроса от доходов Функции Торнквиста позволяют установить уровни доходов, при которых начинается приобретение товаров разной цены, а также точки насыщения разных групп товаров. Применяют функции Торнквиста: 1. Для малоценных товаров 2. Для товаров первой 3. Для товаров второй необходимости 4. Для товаров роскоши Здесь - b 0, b 1, b 2, b 3, минимальный доход, начиная с которого начинается удовлетворение спроса на товары различных групп b 0, < b 1<, b 2, < b 3, - а 0, а 1, а 2, а 3 уровни насыщения товарами соответствующих групп товаров а 0 < а 1< а 2< а 3 - c 0 , c 1 , c 2 , c 3 - уровни риска при покупке товара, c 0 , < c 1< , c 2 <, c 3

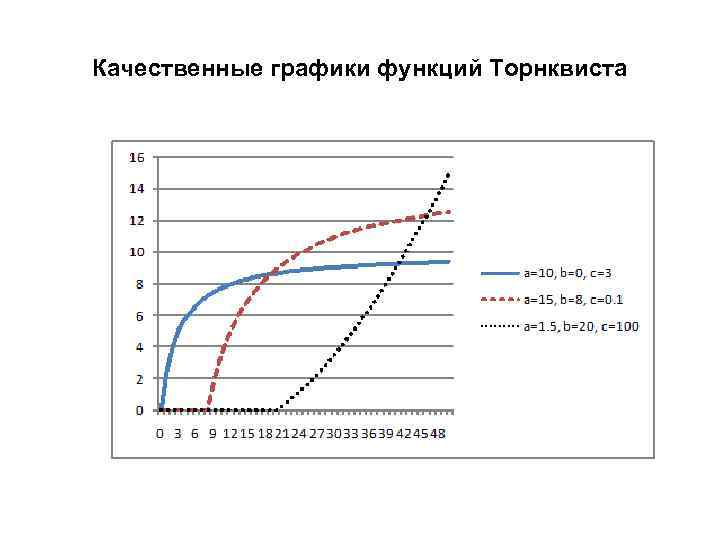Качественные графики функций Торнквиста

4. 5. Производственная функция (ПФ) Производственная функция y=f(x) это функция , характеризующая производственную систему, преобразующую ресурс в выпуск Независимая переменная x соответствует значению затрачиваемого или используемого продукта (фактора производства). Зависимая переменная y– это объем выпускаемой продукции Производственная функция нескольких переменных y=f(x) = f(x 1 , x 2 …xn) имеет тот же смысл при использовании нескольких ресурсов в производственном процессе. Такую производственную функцию называют многофакторной, многоресурсной.

4. 5. Производственная функция Кобба - Дугласа(ПФКД) При построении ПФ на макроуровне, для региона (страны) используют следующие переменные: - Y – совокупный продукт (доход), исчисляемый в неизменных ценах - K - объем используемого в течении года основного капитала - L - живой труд, количество единиц затрачиваемого живого труда в стоимостном выражении Для моделирования региона или страны часто используют производственную функцию Кобба – Дугласа (ПФКД) (1) Если a 1+a 2 =1, то производственную функцию приводят к виду (2) Здесь производительность труда, капиталовооруженность труда производительность капитала

4. 6. Экономический смысл производной Пример 6. 1. Задача о производительности труда Пусть функция u = u(t) выражает количество произведенной продукции u за время t. Пусть необходимо найти z(t 0) - производительность труда z в момент времени t 0 За период времени от t 0 до t 0 + t количество произведенной продукции измениться от u 0 = u(t 0) до u(t 0 + t ) = u 0 + u Тогда средняя производительность труда за период времени от t 0 до t 0 + t равна Zср = u / t. Производительность труда z в момент времени t 0 можно определить как предельное значение средней производительности за указанный выше период времени • Zt 0 = lim Zср = lim u / t • t 0

4. 6. Экономический смысл производной Пример 6. 2. Задача о предельных издержках производства Пусть y – издержки производства, х – количество (объем) выпускаемой продукции, y=f(x) – производственная функция, зависимость издержек от объема производства Тогда х – прирост продукции; y- приращение издержек производства; y/ х - среднее приращение издержек производства на единицу продукции; Производная выражает предельные издержки производства, характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции

4. 7. Применение производной. Эластичность Определение. Эластичность функции – предел отношения относительного приращения функции y к относительному приращению аргумента x при Основные свойства эластичности: 1. Эластичность произведения двух функций равна сумме эластичности этих функций Ex(uv) = Ex(u) + Ex(v) 2. Эластичность частного равна разности эластичностей 3. Эластичность взаимообратных функций – взаимообратные величины 4. Темп изменения функции равен. Тогда эластичность равна

4. 7. Применение производной. Эластичность применяется в в многих задачах, в том числе в задаче спроса и предложения. В этих задачах эластичность приближенно показывает, на сколько процентов изменится спрос (объем потребления) при изменение цены (дохода) на 1 %. При решении прикладных задач считается, что если то спрос эластичный то спрос неэластичный то спрос с единичной эластичностью Знак коэффициента эластичности показывает направление влияния Ex(y) < 0 означает, что увеличение одной переменной приводит к уменьшению второй

4. 7. Применение производной. Эластичность Пример 7. 1. Зависимость между себестоимостью единицы продукции y (тыс. руб. ) и выпуском продукции x (млрд. руб. ) задается функцией y = -0. 5 x +80 Найти эластичность себестоимости при выпуске продукции, равном 60 млн. руб. Решение. Эластичность себестоимости При х=60 Ex=60(y)= -0. 6. Таким образом, при выпуске продукции, равном 60 млн. руб. увеличение выпуска на 1% приведет к снижению себестоимости на 0. 6%

4. 8. Применение дифференциала. Абсолютная и относительная погрешности При вычислении y=f(x) истинное значение аргумента х известно в некотором приближении. Тогда и значение функции y=f(x) будем получать в некотором приближении. Оперируют при этом абсолютной погрешностью и относительной погрешностью и Вычислить относительную погрешность определения расхода бензина при скорости 90 км/ч, если относительная погрешность изменения скорости равна 5% и уравнение движения автомобиля y=18 -0. 3 x+0. 003 x 2. Эластичность функции по абсолютной величине

4. 9. Применение определенного интеграла в экономических задачах Определенный интеграл используется для решения целого ряда прикладных задач: 1. Вычисление объема произведенной продукции при известной функции производительности труда 2. Вычисление коэффициента Джини (оценка степени неравенства при распределении доходов 3. Определение дисконтированного дохода за определенный промежуток времени 4. Вычисление среднего времени на изготовление одного изделия в период освоения

Определенный интеграл. 1. Объем продукции Пример 9. 1. Производительность труда задана функцией Кобба – Дугласа g(t) = (1+t)e 3 t Требуется определить объем продукции Q, произведенной за период времени Т=4 года. Решение. Общее решение задачи Тогда Интеграл берется по частям. Студентам необходимо выполнить эту работу самостоятельно и представит преподавателю

Определенный интеграл. 3. Дисконтированный доход Дисконтирование – определение начальной суммы по ее конечной величине , полученной через t лет при годовой процентной ставке p Постановка задачи. Обозначим Kt – конечная сумма, полученная за t лет K – начальная сумма i=p/100 – удельная процентная ставка Накопления за t лет в случае : - простых процентов Kt =К (1 + it); K= Kt / (1 + it) ; - сложных процентов Kt = К (1 + i)t ; K= Kt / (1 + i)t - Дисконтированный доход за время Т, в случае непрерывного начисления процентов , определяется по формуле Здесь f(t) - непрерывно изменяющийся во времени доход

Дисконтированный доход. Пример 9. 3 Определить дисконтированный доход за три года при процентной ставке р=8%, если первоначальные (базовые) вложения составили 10 млн. руб. и намечается ежегодно увеличивать капиталовложения на 1 млн. руб. Решение. Капиталовложения задаются функцией f(t) = 10 + t. Дисконтированная сумма капиталовложений Интерпретация полученного результата: Получение одинаковой наращенной суммы при ежегодных капиталовложениях от 10 до 13 млн. руб. равносильны одновременным первоначальным вложениям К= 30. 5 млн. руб. при той же непрерывной процентной ставке Примечание. Решить задачу самостоятельно. Применить метод интегрирования по частям

Определенный интеграл. Теорема о среднем значении. • Если f(x) - непрерывна на [a, b] , то на этом отрезке существует точка a ≤ ≤ b такая, что прямоугольник с основанием (b – a) и высотой f( ) равновелик площади криволинейной трапеции (рис. 6). • Математически это можно записать • Площадь криволинейной трапеции • Среднее значение

Применение теоремы о среднем: среднее время на освоение новой продукции Данные задачи: t(x) – функция изменения затрат времени на изготовления изделия в зависимости от степени освоения производства x 1, x 2 – количество изделий в ходе налаживания производства tср – среднее время на освоение партий от x 1, до x 2 изделий Решить самостоятельно задачу. Найти tср , если x 1=100, x 2 = 121 изделий; t(x) = ax-b где a –затраты времени на первое изделие, а=600 (мин) b – показатель производственного процесса, b = 0. 5 Ответ: ,