Тема 4 Методика детерминированного факторного анализа 1 Детерминированное

Тема 4. Методика детерминированного факторного анализа 1. Детерминированное факторное моделирование 2. Классические методы факторного анализа

АН РОВ И ДЕЛ МО ИЕ , с я АКТ ани браз) Ф н о поз НОЕ о ВАН ый г О НИР чно условн И нау ь ( ЕРМ Т д 1. ДЕ ето модел – м ется ние созда а ели ров рого я. мод ров, ели кото вани ой акто рме од ью н ф М едо тор щ фо ак ля и мо а иссл в ф по те я ект а с объ ной показ редает ван ого пе. ро ем ини леду ину, нения ч м ели урав сс тер де зь и го в ого е В ческ освя щих и мат заим еляю е в д мат е опр етного онкр к Е РНО О

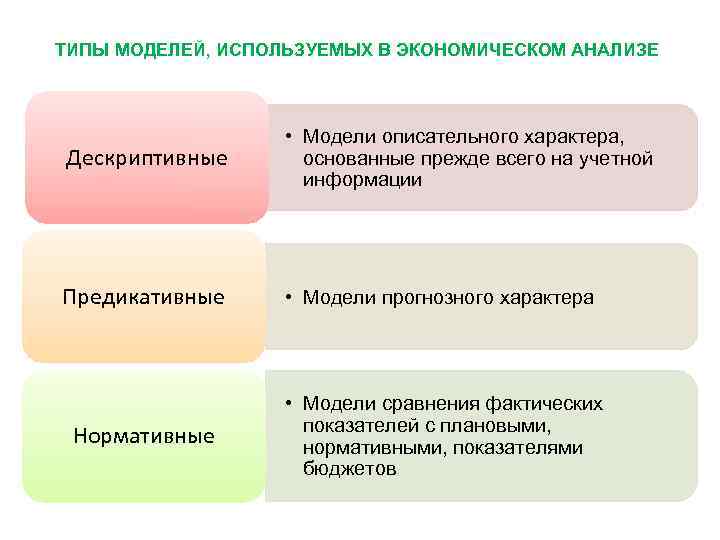ТИПЫ МОДЕЛЕЙ, ИСПОЛЬЗУЕМЫХ В ЭКОНОМИЧЕСКОМ АНАЛИЗЕ Дескриптивные • Модели описательного характера, основанные прежде всего на учетной информации Предикативные • Модели прогнозного характера Нормативные • Модели сравнения фактических показателей с плановыми, нормативными, показателями бюджетов

ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ДЕТЕРМИНИРОВАННЫМ ФАКТОРНЫМ МОДЕЛЯМ Факторы, которые включаются в модель, должны иметь определенно выраженный характер Факторы, входящие в модель, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями Все факторы должны быть количественно измеримыми Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов

ЭТАПЫ ФАКТОРНОГО АНАЛИЗА 1 • Отбор факторов, определяющих исследуемые результативные показатели 2 • Классификация и систематизация факторов с целью обеспечения возможностей системного подхода 3 • Определение формы зависимости между факторами и результативным показателями 4 • Моделирование взаимосвязи между факторами и результативным показателями 5 • Расчет влияния факторов и оценка роли каждого из них в изменении величины результативного показателя

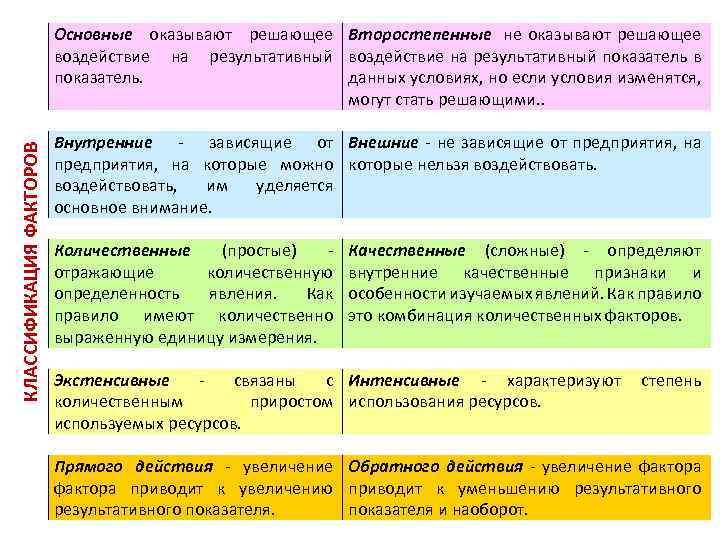КЛАССИФИКАЦИЯ ФАКТОРОВ Основные оказывают решающее Второстепенные не оказывают решающее воздействие на результативный показатель в показатель. данных условиях, но если условия изменятся, могут стать решающими. . Внутренние - зависящие от Внешние - не зависящие от предприятия, на которые можно которые нельзя воздействовать, им уделяется основное внимание. Количественные (простые) отражающие количественную определенность явления. Как правило имеют количественно выраженную единицу измерения. Качественные (сложные) - определяют внутренние качественные признаки и особенности изучаемых явлений. Как правило это комбинация количественных факторов. Экстенсивные связаны с Интенсивные - характеризуют количественным приростом использования ресурсов. используемых ресурсов. степень Прямого действия - увеличение Обратного действия - увеличение фактора приводит к увеличению приводит к уменьшению результативного показателя и наоборот.

ТИПЫ ФАКТОРНЫХ МОДЕЛЕЙ 1. Аддитивные модели - они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей 2. Мультипликативные модели – они применяются тогда, когда результативный показатель представляет собой произведение нескольких факторов

3. Кратные модели – применяются тогда, когда результативный показатель получают делением одного факторного показателя на величину другого 4. Смешанные (комбинированные) модели – это сочетание в различных комбинациях всех предыдущих моделей

МЕТОДЫ ФАКТОРНОГО МОДЕЛИРОВАНИЯ 1. Метод удлинения факторной модели (выражение одного или нескольких факторов через формирующие их элементы) - исходная факторная модель

Анализ затрат на 1 рубль выручки от продаж

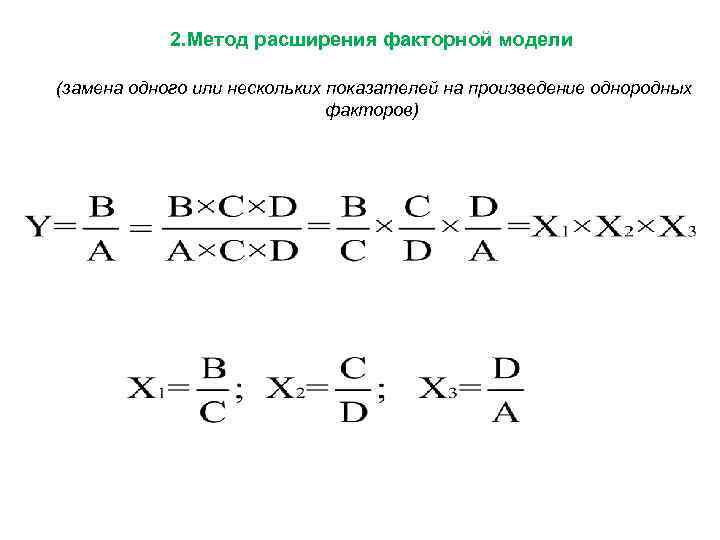2. Метод расширения факторной модели (замена одного или нескольких показателей на произведение однородных факторов)

Анализ рентабельности активов RА = R п Модель Du Pont RА=Rп×kоб. а об K

3. Метод сокращения факторной модели (деление одного или нескольких показателей на однородные факторы)

Анализ фондоотдачи

2. КЛАССИЧЕСКИЕ МЕТОДЫ ФАКТОРНОГО АНАЛИЗА БАЛАНСОВЫЙ МЕТОД Применяется в моделях аддитивного типа Исходная факторная модель Y 0=А 0+В 0+ С 0 Конечная факторная модель Y 1=А 1+В 1+ С 1 Определим, как повлияло изменение факторов А, В, С на изменение результативного показателя Y. Для этого определим абсолютное изменение показателей. DА=А 1 -A 0 B=B 1 -В 0 C=C 1 -С 0 Определим совокупное влияние факторов уравнение балансовой увязки Знак ± показывает направление влияния данного фактора на результативный показатель. Для оценки все факторы классифицируют на факторы прямого и обратного действия

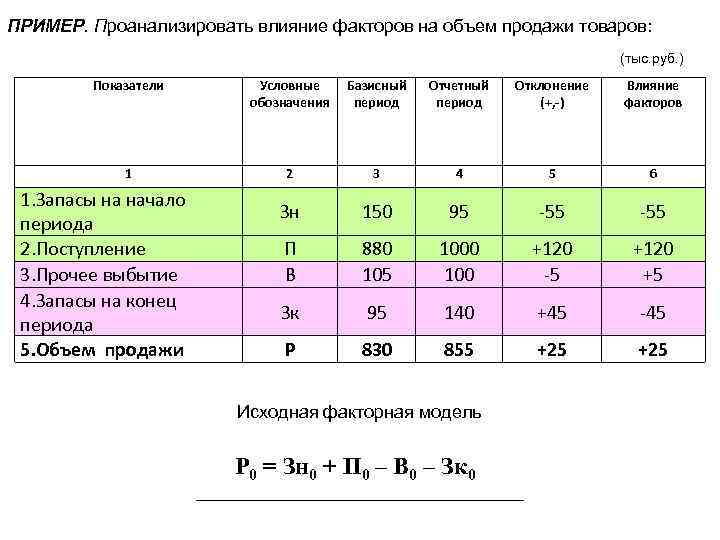ПРИМЕР. Проанализировать влияние факторов на объем продажи товаров: (тыс. руб. ) Показатели Условные обозначения Базисный период Отчетный период Отклонение (+, -) Влияние факторов 1 2 3 4 5 6 Зн 150 95 -55 П В 880 105 1000 100 +120 -5 +120 +5 Зк 95 140 +45 -45 Р 830 855 +25 1. Запасы на начало периода 2. Поступление 3. Прочее выбытие 4. Запасы на конец периода 5. Объем продажи Исходная факторная модель Р 0 = Зн 0 + П 0 – В 0 – Зк 0

ВЫВОД. Объем продажи товаров в отчетном периоде возрос на 25 тыс. руб. На этот прирост повлияли следующие факторы: -из-за сокращения запасов на начало периода продажа товаров снизилась на 55 тыс. руб. , (фактор прямого действия) -прирост поступления товаров привел к повышению продажи товаров на 120 тыс. руб. , (фактор прямого действия) -сокращение потерь привело к увеличению продажи товаров на 5 тыс. руб. , (фактор обратного действия) -увеличение периода привело остатков товаров (нереализованных) на конец к снижению продажи тыс. руб. (фактор обратного действия) товаров на 45

МЕТОД ЦЕПНОЙ ПОДСТАНОВКИ (Можно использовать в моделях любого типа) Метод состоит из следующих последовательных шагов: 1. Строят исходную факторную модель. 2. Последовательно производят замену базисной величины одного показателяфактора его фактической (отчетной) величиной, все остальные факторы при этом остаются неизменными. 3. Используя факторную модель, по каждой подстановке производят расчет результативного показателя. 4. Степень влияния факторов на результат определяется последовательным вычитанием: -из результата первой «подстановки» вычитается базисный результат, -из второго расчетного результата вычитается первый, -из третьего – второй и т. д. . Из каждого последующего вычитается предыдущий результат.

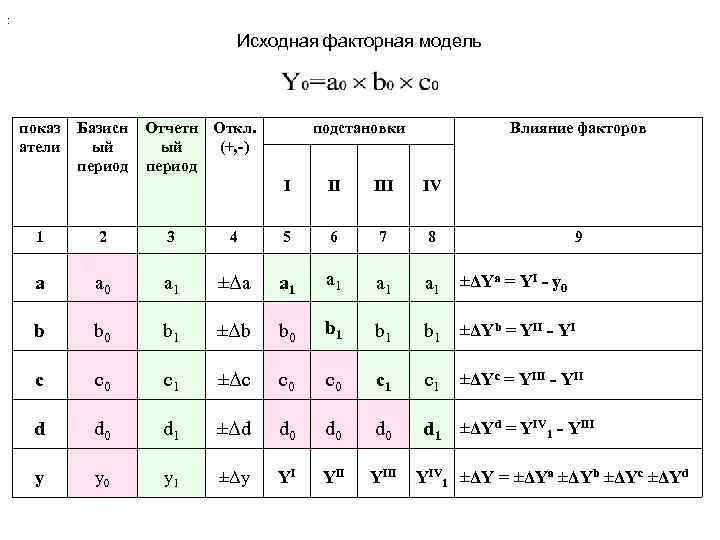: Исходная факторная модель показ атели Базисн ый период Отчетн Откл. ый (+, -) период подстановки Влияние факторов I II IV 1 2 3 4 5 6 7 8 9 a a 0 a 1 ±Δa a 1 a 1 b b 0 b 1 ±Δb b 0 b 1 b 1 ±ΔYb = YII - YI c c 0 c 1 ±Δc c 0 c 1 d d 0 d 1 ±Δd d 0 d 0 d 1 ±ΔYd = YIV 1 - YIII y y 0 y 1 ±Δy YI YIII ±ΔYa = YI - y 0 ±ΔYc = YIII - YII YIV 1 ±ΔY = ±ΔYa ±ΔYb ±ΔYc ±ΔYd

Замечания При использовании метода цепных подстановок имеет значение последовательность замены факторов. Сначала заменяют количественные, затем качественные факторы, чтобы уменьшить их влияние на точность результата анализа. Основной недостаток: возможное искажение результата анализа под воздействием дополнительного эффекта от взаимного влияния факторов, который проявляется тем сильнее, чем дальше от начала расчетов определяется влияние данного фактора.

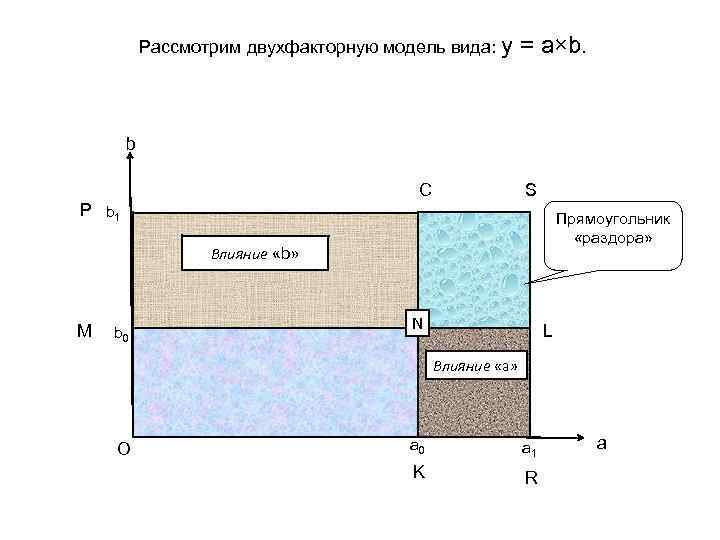Рассмотрим двухфакторную модель вида: y = a×b. b С S Р b 1 Прямоугольник «раздора» Влияние «b» М b 0 N L Влияние «а» О a 0 a 1 K R a

Прямоугольник OMNK : Y 0 = a 0 × b 0, т. е. базисное значение результата; Прямоугольник OPSR : Y 1 = a 1 × b 1, т. е. отчетное значение результата; Первая подстановка : YI =a 1×b 0 Влияние фактора «а» : ±ΔYa = YI - y 0 прямоугольник KNLR; Влияние фактора «b» : ±ΔYb = Y 1 - YI прямоугольник MPSL Если мы поменяем местами факторы «a» и «b» , то есть поменяем последовательность замены, то появится «прямоугольник раздора» NCSL. Причем с увеличением количества факторов этот прямоугольник будет увеличиваться в геометрической прогрессии. Поэтому экономисты условились, что сначала оценивается влияние количественных факторов, а затем — качественных.

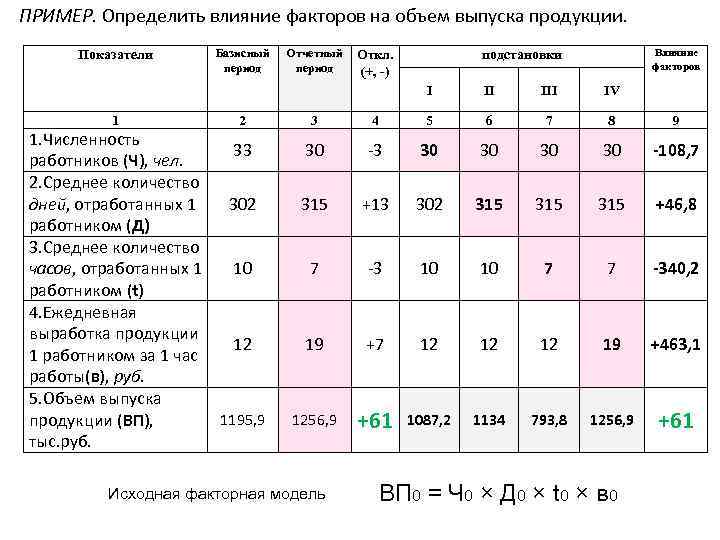ПРИМЕР. Определить влияние факторов на объем выпуска продукции. Показатели Базисный период Отчетный период Откл. (+, -) Влияние факторов подстановки I 1 1. Численность работников (Ч), чел. 2. Среднее количество дней, отработанных 1 работником (Д) 3. Среднее количество часов, отработанных 1 работником (t) 4. Ежедневная выработка продукции 1 работником за 1 час работы(в), руб. 5. Объем выпуска продукции (ВП), тыс. руб. II IV 2 3 4 5 6 7 8 9 33 30 -3 30 30 -108, 7 302 315 +13 302 315 315 +46, 8 10 7 -3 10 10 7 7 -340, 2 12 19 +7 12 12 12 19 +463, 1 1195, 9 1256, 9 +61 1087, 2 1134 793, 8 1256, 9 +61 Исходная факторная модель ВП 0 = Ч 0 × Д 0 × t 0 × в 0

Расчет влияния факторов 1) Влияние изменения численности работников ΔВПЧ = 1087, 2 – 1195, 9 = -108, 7 тыс. руб. 2) Влияние изменения количества рабочих дней: ΔВПД = 1134 - 1087, 2 = +46, 8 тыс. руб. 3) Влияние изменения количества часов, отработанных одним рабочим : ΔВПt = 793, 8 – 1134 = -340, 2 тыс. руб. 4) Влияние изменения среднечасовой выработки: ΔВПВ = 1256, 9 - 793, 8 = +463, 1 тыс. руб. Определяем совокупное влияние факторов на результат: ΔВП = ΔВПЧ + ΔВПД +ΔВПt+ΔВПВ = -108, 7 + 46, 8 – 340, 2 +463, 1 = +61 тыс. руб.

ВЫВОДЫ. Объем выпуска продукции увеличился на 61 тыс. руб. На это повлияли следующие факторы: - сокращение численности работников на 3 чел. привело к снижению выпуска продукции на 108, 7 тыс. руб. -увеличение количества рабочих дней в отчетном периоде на 13 дней привело к увеличению выпуска продукции на 46, 8 тыс. руб. -сокращение на 3 часа времени работы каждого работника в отчетном периоде привело к снижению выпуска продукции на 340, 2 тыс. руб. - повышение среднечасовой выработки каждого работника в отчетном периоде на 7 руб. привело к увеличению объема выпуска продукции на 463, 1 тыс. руб.

МЕТОД АБСОЛЮТНЫХ РАЗНИЦ (Это сокращенный вариант метода цепных подстановок и используется в мультипликативных моделях) Метод состоит из следующих последовательных шагов: 1. Строят исходную факторную модель. 2. Влияние фактора определяют путем умножения абсолютного изменения данного фактора на базисное значение факторов, которые стоят справа от него и на фактическое значение факторов. , которые стоят слева от него. Последовательность расчетов такая же как в методе цепной подстановки: сначала определяют влияние количественных факторов, затем качественных. Методу абсолютных разниц присущ тот же недостаток, что и методу цепной подстановки.

Исходная факторная модель 1. Определим абсолютные изменения показателей 2. Определим влияние фактора «a» 3. Определим влияние фактора «b» 4. Определим влияние фактора «с» 5. Определим совокупное влияние факторов

МЕТОД ОТНОСИТЕЛЬНЫХ РАЗНИЦ (Используется в мультипликативных и некоторых смешанных моделях , как правило в тех случаях когда исходные данные уже содержат определенные ранее относительные изменения факторных показателей в процентах или долях единицы) Исходная факторная модель 1. Определим относительные изменения показателей

2. Определим влияние фактора «a» 3. Определим влияние фактора «b» 4. Определим влияние фактора «с» 5. Определим совокупное влияние факторов

ИНТЕГРАЛЬНЫЙ МЕТОД (Используется в мультипликативных, некоторых смешанных и кратных моделях) Позволяет получить более точный результат, т. к. он не будет зависеть от порядка замены факторов и дополнительный прирост результативного факторов, показателя, распределяется образующийся между ними от взаимодействия пропорционально изолированному воздействию на результативный показатель. их

Исходная факторная модель 1. Определим абсолютные изменения показателей 2. Определим влияние фактора «a» 3. Определим влияние фактора «b» 4. Определим совокупное влияние факторов

ПРИМЕР. Рассчитать влияние факторов на объем продажи продукции: Показатели 1. Реализовано, продукции, кг 2. Цена за 1 кг, руб. 3. Выручка от продажи, руб. Базисный период Отчетный период 2504 6, 50 16276 3007 7, 20 21650 Отклонение Влияние (+, -) факторов +503 +0, 70 +5374 1. Определим влияние изменения количества проданной продукции 2. Определим влияние изменения цены на продукцию 3. Определим совокупное влияние факторов +3445, 55 +1928, 85 +5374

ВЫВОДЫ. Выручка от продаж выросла на 5375 руб. На это оказали влияние следующие факторы: -из-за увеличения количества проданной продукции выручка от продаж выросла на 3445, 55 руб. -из-за повышение цены за 1 кг на 70 копеек в отчетном периоде выручка от продаж выросла на 1928, 85 руб.