ТЕМА 4. Логический и эвристический
ТЕМА 4. Логический и эвристический методы рассуждения в ИИС. Рассуждения на основе дедукции, индукции, аналогии (4 часа)
Основные вопросы: 1. Понятие формальной логической модели. 2. Исчисление предикатов первого порядка. 3. Логический и эвристический методы рассуждения в ИИС. 4. Дедукция, индукция, аналогия. 5. Рассуждения на основе дедукции, индукции, аналогии.
Понятие формальной логической модели Формальная логическая модель – это модель представления знания, использующая аппарат формальной математической логики для представления знаний и вывода. Традиционно в представлении знаний использовались эти модели, основанные на классическом исчислении предикатов 1 -го порядка, когда предметная область или задача описывались в виде набора аксиом, в качестве логических связок использовались логические операции (и, или, исключительное или).
Исчисление предикатов 1 -го порядка в промышленных экспертных системах практически не используется. Эта логическая модель применяется в основном в исследовательских системах, т. к. предъявляет высокие требования и ограничения к предметной области. В промышленных экспертных системах используются различные модификации этих моделей, реализуемых с помощью таких программных средств, как Prolog.
Предикатом (или логичесской функцией) - называется функция от любого числа аргументов, принимающая значения «истина» или «ложь» Выводом системы представления знаний на предикатах - являются формулы, выводимые из аксиом спомощью правил вывода.
Индукция (лат. наведение) – это форма мышления, посредством которой мысль наводится на какое-либо общее правило, общее положени, присущее всем единичным предметам какого либо класса. Дедукция (лат. выведение) – такая форма мышления, когда новая мысль выводится чисто логическим путем (по законам логики) из предшествующих мыслей. Такая последовательность мыслей называется выводом.
Аналогия (греч. соответствие) – сходство нетождественных объектов в некоторых сторонах. Умозаключение по аналогии – вывод о наличии определенных признаков на основе фиксации сходства, существующего в некоторых других признаках. Схема вывода по аналогии: • Объект В обладает признаками a, b, c, d. • Объект С обладает признаками b, c, d, e. • Следовательно, объект С, вероятно, обладает признаком a.
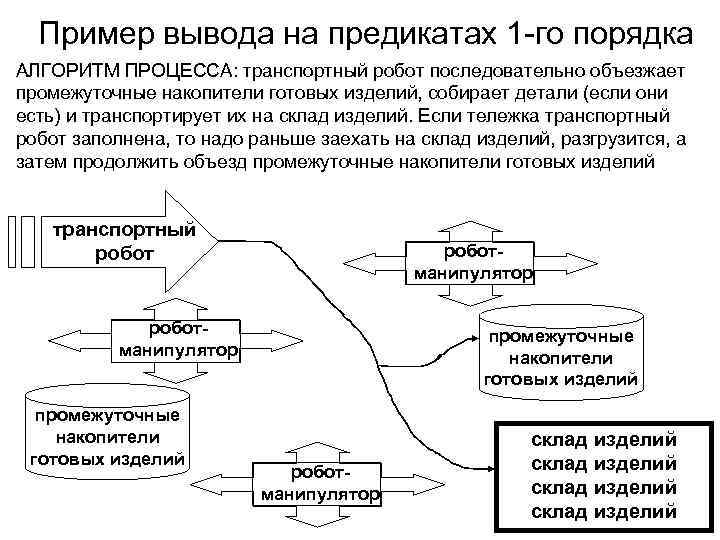
Пример вывода на предикатах 1 -го порядка АЛГОРИТМ ПРОЦЕССА: транспортный робот последовательно объезжает промежуточные накопители готовых изделий, собирает детали (если они есть) и транспортирует их на склад изделий. Если тележка транспортный робот заполнена, то надо раньше заехать на склад изделий, разгрузится, а затем продолжить объезд промежуточные накопители готовых изделий транспортный робот робот- манипулятор робот- промежуточные манипулятор накопители готовых изделий промежуточные накопители склад изделий готовых изделий склад изделий робот- манипулятор склад изделий
Введём следующие предикаты A=пуст (накопитель) B=пуста (тележка транспортного робота) C=освободить (накопитель) D=перейти ((i+1)-й накопитель) E=перевезти (на склад) F=вернуться (i-й накопитель) Тогда сформулированные правила можно записать так: 1. A→D 2. ¬A^B→C^D 3. ¬B→E^F Переведём предикаты в форму предложений: A→D≡¬Av. D
¬A^B→C^D≡¬(¬A^B)v(C^D)=(A^¬B)v(C^D)=(Av¬Bv. C)^(Av¬Bv. D ) Последовательно можно представить в виде 2 ППФ: 1. Av¬Bv. C, Av¬Bv. D 2. ¬B→E^F≡Bv(E^F)=(Bv. E) ^(Bv. F) что также развивается на две ППФ Bv. E, Bv. F. Теперь система правил будет иметь вид: 1. ¬Av. D 2. Av¬Bv. C, Av¬Bv. D 3. Bv. E, Bv. F
Достоинства системы представления знаний на основе исчисления предикатов: 1. Они достаточно хорошо исследованы как формальная система. 2. Существуют ясные правила, то есть результаты операций над БЗ такжк достаточно ясно определены. Недостатком исчисления предикатов является ограниченная выразимость, т. к. существует много факторов, которые трудно или невозможно выразить предикатами.